Современные научные картины мира

1. Пространство и время в современной научной

картине мира.

Пространство и время как всеобщие и необходимые формы бытия материи являются фундаментальными категориями в современной физике и других науках. Физические, химические и другие величины непосредственно или опосредованно связаны с измерением длин и длительностей, т.е. пространственно-временных характеристик объектов. Поэтому расширение и углубление знаний о мире связано с соответствующими учениями о пространстве и времени.

1.1. Развитие взглядов на пространство и время в истории науки

Даже в античном мире мыслители задумывались над природой и сущностью пространства и времени. Так, одни из философов отрицали возможность существования пустого пространства или, по их выражению, небытия. Это были представители элейской школы в Древней Греции. А знаменитый врач и философ из г. Акраганта, Эмпедокл, хотя и поддерживал учение о невозможности пустоты, в отличие от элеатов утверждал реальность изменения и движения. Он говорил, что рыба, например, передвигается в воде, а пустого пространства не существует.

Некоторые философы, в том числе Демокрит, утверждали, что пустота существует, как материи и атомы, и необходима для их перемещений и соединений.

В доньютоновский период развитие представлений о пространстве и времени носило преимущественно стихийный и противоречивый характер. И только в "Началах" древнегреческого математика Евклида пространственные характеристики объектов впервые обрели строгую математическую форму. В это время зарождаются геометрические представления об однородном и бесконечном пространстве.

Геоцентрическая система К. Птолемея, изложенная им в труде "Альмагест", господствовала в естествознании до XVI в. Она представляла собой первую универсальную математическую модель мира, в которой время было бесконечным, а пространство конечным, включающим в себя равномерное круговое движение небесных тел вокруг неподвижной Земли.

Коренное изменение пространственной и всей физической картины произошло в гелиоцентрической системе мира, развитой Н. Коперником в работе "Об обращениях небесных сфер". Принципиальное отличие этой системы мира от прежних теорий состояло в том, что в ней концепция единого однородного пространства и равномерности течения времени обрела реальный эмпирический базис.

Признав подвижность Земли, Коперник в своей теории отверг все ранее существовавшие представления о ее уникальности, "единственности" центра вращения во Вселенной. Тем самым теория Коперника не только изменила существовавшую модель Вселенной, но и направила движение естественнонаучной мысли к признанию безграничности и бесконечности пространства.

Космологическая теория Д. Бруно связала воедино бесконечность Вселенной и пространства. В своем произведении "О бесконечности, Вселенной и мирах" Бруно писал: "Вселенная должна быть бесконечной благодаря способности и расположению бесконечного пространства и благодаря возможности и сообразности бытия бесчисленных миров, подобных этому..."¹. Представляя Вселенную как "целое бесконечное", как "единое, безмерное пространство", Бруно делает вывод и о безграничности пространства, ибо оно "не имеет края, предела и поверхности".

Практическое обоснование выводы Бруно получили в "физике неба" И. Кеплера и в небесной механике Г. Галилея. В гелиоцентрической картине движения планет Кеплер увидел действие единой физической силы. Он установил универсальную зависимость между периодами обращения планет и средними расстояниями их до Солнца, ввел представление об их эллиптических орбитах. Концепция Кеплера способствовала развитию математического и физического учения о пространстве.

Подлинная революция в механике связана с именем Г. Галилея. Он ввел в механику точный количественный эксперимент и математическое описание явлений. Первостепенную роль в развитии представлений о пространстве сыграл открытый им общий принцип классической механики — принцип относительности Галилея. Согласно этому принципу все физические (механические) явления происходят одинаково во всех системах, покоящихся или движущихся равномерно и прямолинейно с постоянной по величине и направлению скоростью. Такие системы называются инерциальными. Математические преобразования Галилея отражают движение в двух инерциальных системах, движущихся с относительно малой скоростью (меньшей, чем скорость света в вакууме). Они устанавливают инвариантность (неизменность) в системах длины, времени и ускорения.

Дальнейшее развитие представлений о пространстве и времени связано с рационалистической физикой Р. Декарта, который создал первую универсальную физико-космологическую картину мира. В основу ее Декарт положил идею о том, что все явления природы объясняются механическим воздействием элементарных материальных частиц. Взаимодействием элементарных частиц Декарт пытался объяснить все наблюдаемые физические явления: теплоту, свет, электричество, магнетизм. Само же взаимодействие он представлял в виде давления или удара при соприкосновении частиц друг с другом и ввел таким образом в физику идею близкодействия.

Декарт обосновывал единство физики и геометрии. Он ввел координатную систему (названную впоследствии его именем), в которой время представлялось как одна из пространственных осей. Тезис о единстве физики и геометрии привел его к отождествлению материальности и протяженности. Исходя из

этого тезиса он отрицал пустое пространство и отождествил пространство с протяженностью.

Декарт развил также представление о соотношении длительности и времени. Длительность, по его мнению, "соприсуща материальному миру. Время же — соприсуще человеку и потому является модулем мышления". "... Время, которое мы отличаем от длительности, — пишет Декарт в "Началах философии", — есть лишь известный способ, каким мы эту длительность мыслим... ".

Таким образом, развитие представлений о пространстве и времени в доньютоновский период способствовало созданию концептуальной основы изучения физического пространства и времени. Эти представления подготовили математическое и экспериментальное обоснование свойств пространства и времени в рамках классической механики.

Новая физическая гравитационная картина мира, опирающаяся на строгие математические обоснования, представлена в классической механике И. Ньютона. Ее вершиной стала теория тяготения, провозгласившая универсальный закон природы — закон всемирного тяготения. Согласно этому закону сила тяготения универсальна и проявляется между любыми материальными телами независимо от их конкретных свойств. Она всегда пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.

Распространив на всю Вселенную закон тяготения, Ньютон рассмотрел и возможную ее структуру. Он пришел к выводу, что Вселенная является не конечной, а бесконечной. Лишь в этом случае в ней может существовать множество космических объектов — центров гравитации. Так, в рамках ньютоновской гравитационной модели Вселенной утверждается представление о бесконечном пространстве, в котором находятся космические объекты, связанные между собой силой тяготения.

В 1687 г. вышел основополагающий труд Ньютона "Математические начала натуральной философии". Этот труд более чем на два столетия определил развитие всей естественнонаучной картины мира. В нем были сформулированы основные законы движения и дано определение понятий пространства, времени, места и движения.

Раскрывая сущность времени и пространства, Ньютон характеризует их как "вместилища самих себя и всего существующего. Во времени все располагается в смысле порядка последовательности, в пространстве — в смысле порядка положения".

Онпредлагает различать два типа понятий пространства и времени: абсолютные (истинные, математические) и относительные (кажущиеся, обыденные) и дает им следующую типологическую характеристику:

- Абсолютное, истинное, математическое время само по себе и по своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью.

- Относительное, кажущееся, или обыденное, время есть или точная, или изменчивая, постигаемая чувствами, внешняя мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как-то: час, день, месяц, год.

- Абсолютное пространство по своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным. Относительное пространство есть мера или какая-либо ограниченная подвижная часть, которая определяется нашими чувствами по положению его относительно некоторых тел и которое в обыденной жизни принимается за пространство неподвижное.

Из определений Ньютона следовало, что разграничение им понятий абсолютного и относительного пространства и времени связано со спецификой теоретического и эмпирического уровней их познания. На теоретическом уровне классической механики представления об абсолютном пространстве и времени играли существенную роль во всей причинной структуре описания мира. Оно выступало в качестве универсальной инерциальной системы отсчета, так как законы движения классической механики справедливы в инерциальных системах отсчета. На уровне эмпирического познания материального мира понятия "пространства" и "времени" ограничены чувствами и свойствами познающей личности, а не объективными признаками реальности как таковой. Поэтому они выступают в качестве относительного времени и пространства.

Ньютоновское понимание пространства и времени вызвало неоднозначную реакцию со стороны его современников — естествоиспытателей и философов. С критикой ньютоновских представлений о пространстве и времени выступил немецкий ученый Г.В. Лейбниц. Он развивал реляционную концепцию пространства и времени, отрицающую существование пространства и времени как абсолютных сущностей.

Указывая на чисто относительный (реляционный) характер пространства и времени, Лейбниц пишет: "Считаю пространство так же, как и время, чем-то чисто относительным: пространство — порядком сосуществовании, а время — порядком последовательностей".

Предвосхищая положения теории относительности Эйнштейна о неразрывной связи пространства и времени с материей, Лейбниц считал, что пространство и время не могут рассматриваться в "отвлечении" от самих вещей. "Мгновения в отрыве от вещей ничто, — писал он, — и они имеют свое существование в последовательном порядке самих вещей".

Однако данные представления Лейбница не оказали заметного влияния на развитие физики, так как реляционная концепция пространства и времени была недостаточна для того, чтобы служить основой принципа инерции и законов движения, обоснованных в классической механике Ньютона. Впоследствии это было отмечено и А. Эйнштейном.

Успехи ньютоновской системы (поразительная точность и кажущаяся ясность) привели к тому, что многие критические соображения в ее адрес обходились молчанием. А ньютоновская концепция пространства и времени, на основе которой строилась физическая картина мира, оказалась господствующей вплоть до конца XIX в.

Основные положения этой картины мира, связанные с пространством и временем, заключаются в следующем.

- Пространство считалось бесконечным, плоским, "прямолинейным", евклидовым. Его метрические свойства описывались геометрией Евклида. Оно рассматривалось как абсолютное, пустое, однородное и изотропное (нет выделенных точек и направлений) и выступало в качестве "вместилища" материальных тел, как независимая от них инерциальная система.

- Время понималось абсолютным, однородным, равномерно текущим. Оно идет сразу и везде во всей Вселенной "единообразно и синхронно" и выступает как независимых материальных объектов процесс длительности, Фактически классическая механика сводила время к длительности, фиксируя определяющее свойство времени "показывать чродссти-тельность события”. Значение указаний времени в класс иче ской механике считалось абсолютным, не зависяицш от со стояния движения тела отсчета.

- Абсолютное время и пространство служили оснотой цля преобразований Галилея-Ньютона, посредством которых осуществлялся переход к инерциальным системам. Эти системы выступали в качестве избранной системы координат в классической механике.

- Принятие абсолютного времени и постулирование абсолютной и универсальной одновременности во всей Вселенной явилось основой для теории дальнодействия. В качестве дальнодействующей силы выступало тяготение, которое с 6есконечной скоростью, мгновенно и прямолинейно распространяло силы на бесконечные расстояния. Эти мгновенные, вневременные взаимодействия объектов служили физическим каркасом для обоснования абсолютного пространства, существующего независимо от времени.

До XIX в. физика была в основном физикой вещества, т. е. она рассматривала поведение материальных объектов с конеч ньш числом степеней свободы и обладающих конечной массой покоя. Изучение электромагнитных явлений в XIX в. выявило ряд существенных отличий их свойств по сравнению с механическими свойствами тел.

Если в механике Ньютона силы зависят от расстояний между телами и направлены по прямым, то в электродинамике (теории электромагнитных процессов), созданной в XIX в. английскими физиками М. Фарадеем и Дж. К.Максвеллом, силы зависят от расстояний и скоростей и не направлены ло прямым, соединяющим тела. А распространение сил происходит не мгновенно, а с конечной скоростью. Как отмечал Эйнштейн, с развитием электродинамики и оптики становилось все очевиднее, что "недостаточно одной классической механики для полного описания явлений природы". Из теории Максвелла вытекал вывод о конечной скорости распространения электромагнитных взаимодействий и существовании электромагнитных волн. Свет, магнетизм, электричество стали рассматриваться как проявление единого электромагнитного поля. Таким образом, Максвеллу удалось подтвердить действие законов сохранения и принципа близкодействия благодаря введению понятия электромагнитного поля.

Итак, в физике XIX в. появляется новое понятие — "поля", что, по словам Эйнштейна, явилось "самым важным достижением со времени Ньютона". Открытие существования поля в пространстве между зарядами и частицами было очень существенно для описания физических свойств пространства и времени. Структура электромагнитного поля описывается с помощью четырех уравнений Максвелла, устанавливающих связь величин, характеризующих электрические и магнитные поля с распределением в пространстве зарядов и токов. Как заметил Эйнштейн, теория относительности возникает из проблемы поля.

Специального объяснения в рамках существовавшей в конце XIX в. физической картины мира требовал и отрицательный результат по обнаружению мирового эфира, полученный американским физиком А. Майкельсоном. Его опыт доказал независимость скорости света от движения Земли. С точки зрения классической механики, результаты опыта Майкельсона не поддавались объяснению. Некоторые физики пытались истолковать их как указывающие на реальное сокращение размеров всех тел, включая и Землю, в направлении движения под действием возникающих при этом электромагнитных сил.

Создатель электронной теории материи X. Лоренц вывел математические уравнения (преобразования Лоренца) для вычисления реальных сокращений движущихся тел и промежутков времени между событиями, происходящими на них, в зависимости от скорости движения.

Как показал позднее Эйнштейн, в преобразованиях Лоренца отражаются не реальные изменения размеров тел при движении (что можно представить лишь в абсолютном пространстве), а изменения результата измерения в зависимости от движения системы отсчета.

Таким образом, относительными оказывались и "длина", и "промежуток времени" между событиями, и даже "одновременность" событий. Иначе говоря, не только всякое движение, но и пространство, и время.

1.2. Пространство и врем,я в свете теории

относительностиЭйнштейна

Специальная теория относительности, созданная в 1905 г. А. Эйнштейном, стала результатом обобщения и синтеза классической механики Галилея—Ньютона и электродинамики Максвелла—Лоренца. "Она описывает законы всех физических процессов при скоростях движения, близких к скорости света, но без учета поля тяготения. При уменьшении скоростей движения она сводится к классической механике, которая, таким образом, оказывается ее частным случаем”.

Если бы были найдены абсолютные пространство и время, а следовательно, и абсолютные скорости, то пришлось бы отказаться от принципа относительности, в соответствии с которым инерциальные системы равноправны. Создатель теории относительности сформулировал обобщенный принцип относительности, который теперь распространяется и на электромагнитные явления, в том числе и на движение света. Этот принцип гласит, что никакими физическими опытами (механическими, электромагнитными и др.), производимыми внутри данной системы отсчета, нельзя установить различие между состояниями покоя и равномерного прямолинейного движения. Классическое сложение скоростей неприменимо для распространения электромагнитных волн, света. "Для всех физических процессов скорость света обладает свойством бесконечной скорости. Для того чтобы сообщить телу скорость, равную скорости света, требуется бесконечное количество энергии, и именно поэтому физически невозможно, чтобы какое нибудь тело достигло этой скорости. Этот результат был подтвержден измерениями, которые проводились над электронами. Кинетическая энергия точечной массы растет быстрее, нежели квадрат ее скорости, и становится бесконечной для скорости, равной скорости света".

Скорость света является предельной скоростью распространения материальных воздействий. Она не может складываться ни с какой скоростью и для всех инерциальных систем оказывается постоянной. Все движущиеся тела на Земле по отношению к скорости света имеют скорость, равную нулю.

Замечательный русский поэт Л. Мартынов сказал об этом так.

Это почти неподвижности мука, Мчаться куда-то со скоростью звука, Зная при этом, что есть уже где-то Некто, летящий со скоростью света.

И в самом деле, скорость звука всего лишь 340 м/с. Это неподвижность по сравнению со скоростью света.

Из этих двух принципов — постоянства скорости света и расширенного принципа относительности Галилея — математически следуют все положения специальной теории относительности (СТО). Если скорость света постоянна для всех инерциальных систем, а они все равноправны, то физические величины длины тела, промежутка времени, массы для разных систем отсчета будут различными. Так, длина тела в движущейся системе будет наименьшей по отношению к покоящейся. По формуле:

где /' — длина тела в движущейся системе со скоростью V по отношению к неподвижной системе; / — длина тела в покоящейся системе.

Для промежутка же времени, длительности какого-либо процесса — наоборот. Время будет как бы растягиваться, течь медленнее в движущейся системе по отношению к неподвижной, в которой этот процесс будет более быстрым. По формуле: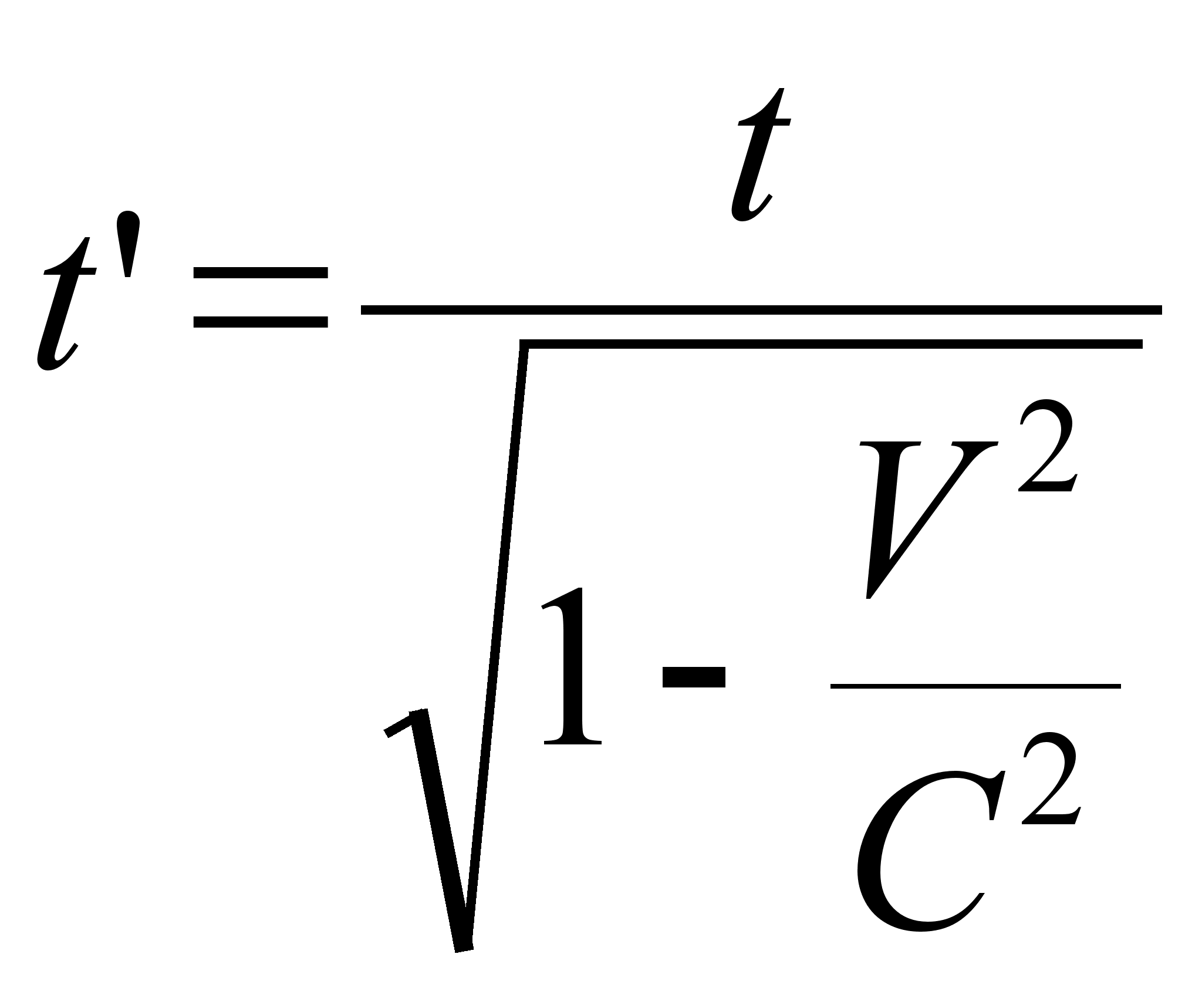

Еще раз подчеркнем, что эффекты специальной теории относительности будут обнаруживаться при скоростях, близких к световым. При скоростях значительно меньше скорости света формулы СТО переходят в формулы классической механики.

Эйнштейн попытался наглядно показать, как происходит замедление течения времени в движущейся системе по отношению к неподвижной. Представим себе железнодорожную платформу, мимо которой проходит поезд со скоростью, близкой к скорости света (см. рис. 1).

Рис. 1.

В точке а₁ на платформе находится наблюдатель N₁ (или прибор, фиксирующий эксперимент). На полу вагона в точке А размещен фонарик. Когда происходит совмещение точки А в вагоне с точкой а₁ на платформе, фонарик включается, появляется луч света. Так как скорость его конечная, хотя и большая, то для того чтобы достигнуть потолка вагона, где расположено зеркало, и отразиться обратно, необходимо время, за которое поезд уйдет вперед.

Для наблюдателя в вагоне луч света пройдет путь 2АВ, а для наблюдателя на платформе — 2А С. Как видно из рисунка, чем больше скорость поезда, тем длиннее линия АС. Очевидно, что 2АС > 2АВ. Это как раз и говорит о замедлении течения времени внутри движущейся системы по отношению к неподвижной.

Необходимо подчеркнуть, что именно в отношении определенных пространственных координат изменяются отрезки длин и промежутки времени. Наблюдатель, находящийся внутри вагона, по своим часам, скажем, ждет полчаса. А по часам наблюдателя на платформе проходит значительно больше времени. Если, например, длина космического корабля в полете уменьшается в два раза с точки зрения наблюдателя на Земле, то при возвращении на Землю корабль сбавляет скорость и его длина становится такой, как и была при отлете.

Время же необратимо. Отсюда известный парадокс близнецов. После путешествия одного из близнецов на ракете, летевшей близко к скорости света, он с удивлением увидит, что его брат стал старше его. Можно даже рассчитать такой полет.

Представим себе, что с Земли стартовал космический корабль со скоростью 0,99 или 0,98 скорости света и вернулся обратно через 50 лет, прошедших на Земле. Но согласно теории относительности по часам корабля этот полет продолжался бы всего лишь год. Если космонавт, отправившись в полет в возрасте 25 лет, оставил на Земле только что родившегося сына, то при встрече 50-летний сын будет приветствовать 26-летнего отца.

Физиологические процессы здесь совершенно ни при чем. Нельзя спрашивать, почему за один год сын космонавта состарился на 50 лет. Теория относительности доказала, что не существует ни абсолютного времени, ни абсолютного пространства. Сын постарел на 50 лет за годы, прожитые на Земле, в системе отсчета корабля время по отношению к земле другое'.

Релятивистское замедление является экспериментальным фактом. В космических лучах в верхних слоях атмосферы образуются частицы, называемые пи-мезонами, или пионами. Собственное время жизни пионов — 10"⁸ с. За это время, двигаясь даже со скоростью, почти равной скорости света, они могут пройти не больше чем 300 см. Но приборы их регистрируют. Они проходят путь, равный 30 км, или в 10 000 раз больше, чем для них возможно. Теория относительности так объясняет этот факт: 10~⁸ с является естественным временем жизни мезона, измеренным по часам, движущимся вместе с мезоном, т. е. покоящимся по отношению к нему. Но в системе отсчета Земли время жизни мезона намного больше, и за это время пионы в состоянии пройти земную атмосферу.

Говоря об относительности пространственных и временных величин в разных системах отсчета, следует помнить, что в теории относительности мы наблюдаем неразрывную связь относительного и абсолютного как одно из проявлений физической симметрии. Поскольку скорость света является абсолютной величиной, то и связь пространства и времени обнаруживается как некоторая абсолютная величина. Она выражается в так называемом пространственно-временном интервале по формуле 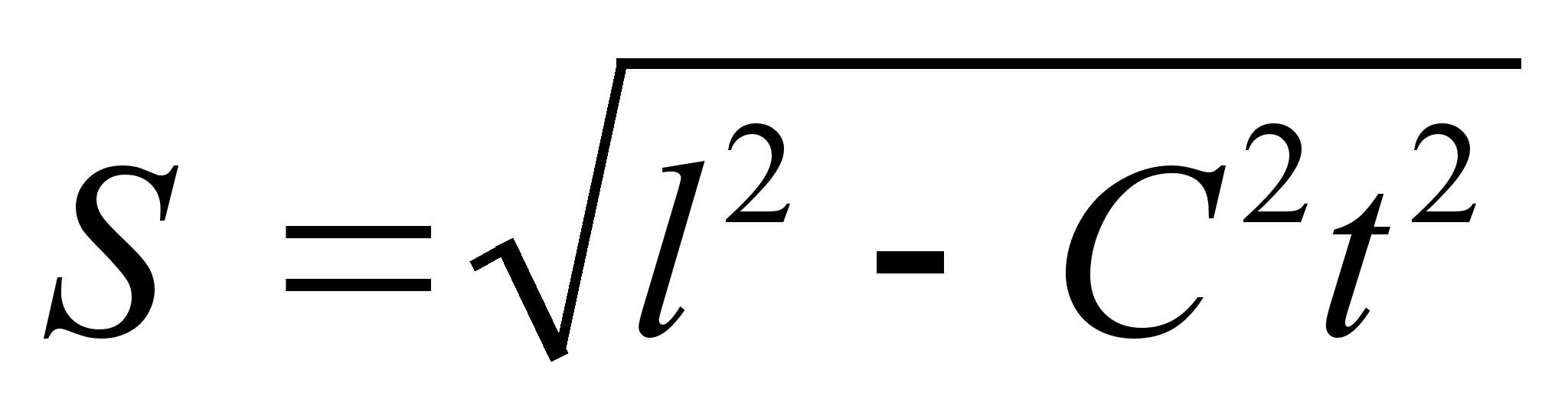. В каждой системе отсчета длина тела и временной промежуток будут различны, а эта величина останется неизменной. Увеличение длины будет соответствовать уменьшение промежутка времени в данной системе, и наоборот.

В общей теории относительности (ОТО), или теории тяготения, Эйнштейн расширяет принцип относительности, распространяя его на неинерциальные системы. В ней он также исходит из экспериментального факта эквивалентности масс инерционных и гравитационных, или эквивалентности инерционных и гравитационных полей.

Правда, принцип эквивалентности справедлив только при строго локальных наблюдениях. Так, представим себе лифт, стоящий на Земле. Наблюдатель в лифте бросает два шара. Они будут двигаться по направлению к центру Земли и, следовательно, друг к другу. Если же мы будем тянуть лифт с ускорением § в пустоте, то те же шары будут двигаться параллельно друг другу (см. рис. 2).

Рис. 2.

Но несмотря на это ограничение, принцип эквивалентности играет важную роль в науке. Мы всегда можем вычислить непосредственно действие сил инерции на любую физическую систему, и это дает нам возможность знать действие поля тяготения, отвлекаясь от его неоднородности, которая часто очень незначительна.

Расширение принципа относительности на неинсрциальные «.'истемы, казалось бы, противоречит нашему обыденному опыту. Находясь внутри инерциальной системы, никаким экспериментом нельзя определить, движется она или покоится. Те, кто летал в самолете, знают, что в нем, как и на Земле, можно делать вес: пить чай, играть в мячик и т. п. Даже если посмотреть в иллюминатор, то увидишь, что самолет как бы висит неподвижно над облаками. Однако, когда самолет начинает сбавлять скорость и идет на посадку, пассажиры сразу же это замечают.

Эйнштейн предлагает провести мысленный эксперимент с лифтом, подвешенным над Землей. Наблюдатели, находящиеся внутри него, не смогут определить в некоторых ситуациях, находятся они в покое или в движении. Представим себе, что в какой-то момент времени канат, на котором подвешен лифт, обрывается, и наблюдатели в нем оказываются в состоянии свободного падения. В этом случае они не смогут определить, какое из двух противоположных утверждений будет истинным: 1) лифт движется в поле тяготения Земли; 2) лифт покоится в отсутствии поля тяготения. Если же в отсутствие поля тяготения Земли лифт будут тянуть вверх с ускорением §, то наблюдатели также не смогут выбрать истинное утверждение из двух противоположных: 1) лифт покоится в поле тяготения Земли; 2) лифт движется с ускорением в отсутствие поля тяготения.

Какие же следствия для пространства и времени вытекают из общей теории относительности? Для этого нужно обратиться вначале к геометрии, которая возникла прежде всего как учение о физическом пространстве, измерении земельных площадей и строительных сооружений. Но уже в древности появилась теоретическая, аксиоматическая геометрия Евклида, которая оставалась единственной до XIX в. Правда, до конца XIX в. не делалось какого-либо различия между теоретической и физической геометрией.

С геометрией Евклида связывался тот взгляд, что пространство везде одно и то же. Она исходила из пяти аксиом или постулатов. Многих математиков не удовлетворял пятый постулат, который гласил, что из одной точки на плоскости можно пронесли только одну прямую, которая не будет пересекаться с джнип, сколько бы ее ни продолжали. Этот постулат не был очевиден, так как никто не мог бы его экспериментально подтвердить даже в воображении — нельзя же линию продолжать в бесконечность.

Ряд известных математиков пытались доказать, что этот постулат на самом деле является теоремой, т. е. его можно вывести из четырех других. Но все их попытки оказались неудачными. Они так или иначе неявно предполагали тот же самый пятый постулат. Например, в той форме, что сумма углов треугольника равна двум прямым. Великий математик К. Гаусс первый поставил под сомнение возможность такого доказательства, т. е. признал, что постулат является аксиомой и, следовательно, его можно заменить другими аксиомами, построив новую геометрию. Но он на это не осмелился.

И лишь Н.И. Лобачевский в России, Б. Риман в Германии и Я. Больяй в Венгрии построили новые геометрии, отбросив пятый постулат и заменив его на другие. Б. Риман заменил его на аксиому, что через точку, лежащую вне данной прямой на плоскости, нельзя провести ни одной параллельной, все они будут пересекаться с данной. Н.И. Лобачевский и Я. Больяй допустили, что существует множество прямых, которые не пересекутся с данной.

Для пояснения отличия этих геометрий возьмем пространство двух измерений, поверхность. Евклидова геометрия реализуется на плоскости, Римана — на поверхности сферы, на которой прямая линия выглядит как отрезок дуги большого круга, центр которого совпадает с центром сферы. Геометрия Лобачевского осуществляется на так называемой псевдосфере. Так как пространство имеет три измерения, то для каждой геометрии вводится понятие кривизны пространства. В евклидовой геометрии кривизна нулевая, у Римана — положительная, у Лобачевского—Больяя — отрицательная.

Поскольку постулат параллельности эквивалентен положению о сумме углов треугольника, то различие этих геометрий наглядно изображается на рисунке. В геометрии Евклида сумма углов треугольника равна 180°, у Римана — она больше, у Лобачевского — меньше. (Рис. 3, а, б, в соответственно).

Рис. 3.

Под кривизной пространства не нужно понимать искривление плоскости наподобие того, как искривлена поверхность евклидовой сферы, где внешняя поверхность отлична от внутренней. Изнутри ее поверхность выгладит вогнутой, извне — выпуклой. Если же брать плоскость в пространстве Лобачевского или Римана, обе ее стороны являются совершенно одинаковыми. Просто внутренняя структура плоскости такова, что мы измеряем ее с помощью некоторого коэффициента "кривизны". Кривизна пространства понимается в науке как отступление его метрики от евклидовой, что точно описывается в языке математики, но не проявляется каким-то наглядным образом.

Риман впоследствии показал единство и непротиворечивость всех неевклидовых геометрий, частным случаем которых является геометрия Евклида.

Создатели геометрий Лобачевский и Риман считали, что только физические эксперименты могут показать нам, какова геометрия нашего мира. Эйнштейн в общей теории относительности сделал геометрию физической экспериментальной наукой, которая подтвердила характер пространства Римана. Здесь опять призовем на помощь мысленный эксперимент. Представим себе, что лифт покоится в отсутствие гравитационного поля (см. рис. 4, а). В стене лифта сделано отверстие А, через которое луч света падает на его противоположную сторону. Линия АВ — прямая. Пусть теперь лифт начинает движение вверх с ускорением §, т. е. 9,8 м/с². За время, пока свет проходит расстояние между стенками, лифт смещается вверх, и луч света попадает уже не в точку В, а в точку С (см. рис. 4, б).

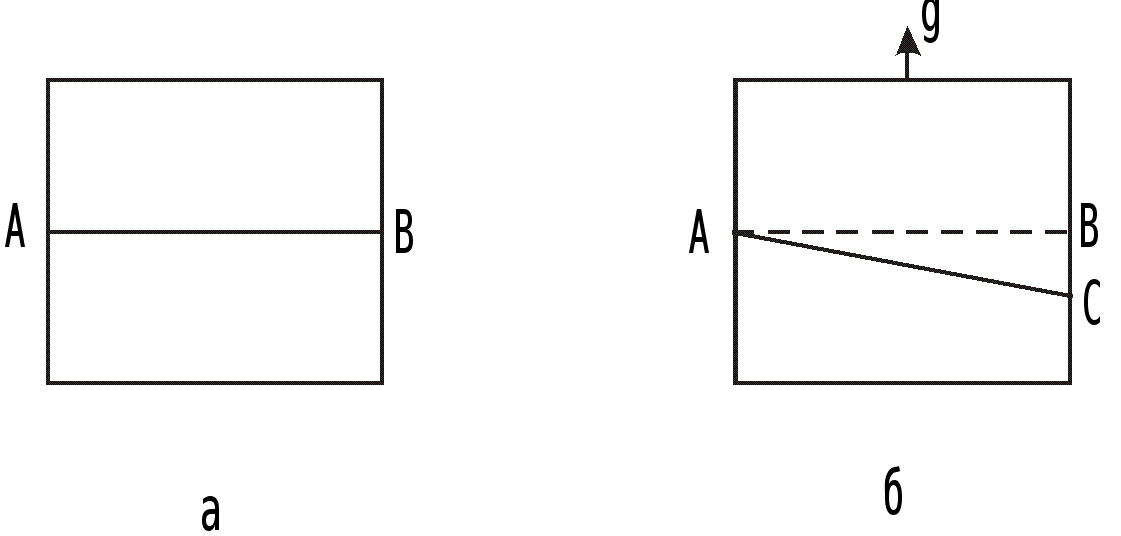
Рис. 4.

Линия АС сохраняет свойство быть кратчайшим расстоянием между двумя точками, но это будет уже не прямая, а прямейшая или геодезическая. На Земле, поверхность которой представляет собой сферу, такие линии и называются геодезическими. Общая теория относительности заменяет закон тяготения Ньютона новым уравнением тяготения. Закон Ньютона получается как предельный случай эйнштейновских уравнений. Рассчитанное теоретически Эйнштейном отклонение луча света было впоследствии экспериментально подтверждено наблюдениями во время солнечного затмения, когда луч света от звезды проходит вблизи поля тяготения Солнца.

В общей теории относительности Эйнштейн доказал, что структура пространства—времени определяется распределением масс материи. Когда корреспондент американской газеты "Нью-Йорк Тайме" спросил Эйнштейна в апреле 1921 г., в чем суть теории относительности, он ответил: "Сугь такова: раньше считали, что если каким-нибудь чудом все материальные вещи исчезли бы вдруг, то пространство и время остались бы. Согласно же теории относительности вместе с вещами исчезли бы и пространство, и время".

1.3. Свойства пространства и времени

Какие же основные свойства пространства и времени мы можем указать? Прежде всего пространство и время объективны и реальны, т. е. существуют независимо от сознания людей и познания ими этой объективной реальности. Человек все более и более углубляет свои знания о ней. Однако в истории науки и философии существовал и другой взгляд на пространство и время — как только субъективных всеобщих форм нашего созерцания.

Согласно этой точке зрения, пространство и время не присущи самим вещам, а зависят от познающего субъекта. В данном случае преувеличивается относительность нашего знания на каждом историческом этапе его развития. Эта точка зрения отстаивается сторонниками философии И. Канта.

Пространство и время являются также универсальными, всеобщими формами бытия материи. Нет явлений, событий, предметов, которые существовали бы вне пространства или вне времени. У Гегеля высшей реальностью является абсолютная идея, или абсолютный дух, который существует вне пространства и вне времени. Только производная от абсолютной идеи природа развертывается в пространстве.

Важным свойством пространства является его трехмерность. Положение любого предмета может быть точно определено только с помощью трех независимых величин — координат. В прямоугольной декартовой системе координат это — X, У, Z., называемые длиной, шириной и высотой. В сферической системе координат — радиус-вектор r и углы a и b (3. В цилиндрической системе — высота г, радиус-вектор и угол а.

В науке используется понятие многомерного пространства (и-мерного). Это понятие математической абстракции играет важную роль. К реальному пространству оно не имеет отношения. Каждая координата, например, 6-мерного пространства может указывать на какое-то любое свойство рассматриваемой физической реальности: температуру, плотность, скорость, массу и т. д. В последнее время была выдвинута гипотеза о реальных 11 измерениях в области микромира в первые моменты рождения нашей Вселенной: 10 — пространственных и одно — временное. Затем из них возникает 4-мерный континуум {лат. сопйпишп — непрерывное, сплошное).

В отличие от пространства, в каждую точку которого можно снова и снова возвращаться (и в этом отношении оно является как бы обратимым), время — необратимо и одномерно. Оно течет из прошлого через настоящее к будущему. Нельзя возвратиться назад в какую-либо точку времени, но нельзя и перескочить через какой-либо временной промежуток в будущее. Отсюда следует, что время составляет как бы рамки для причинно-следственных связей. Некоторые утверждают, что необратимость времени и его направленность определяются причинной связью, так как причина всегда предшествует следствию. Однако очевидно, что понятие предшествования уже предполагает время. Более прав поэтому Г. Рейхенбах, который пишет: "Не только временной порядок, но и объединенный пространственно-временной порядок раскрываются как упорядочивающая схема, управляющая причинными цепями, и, таким образом, как выражение каузальной структуры вселенной".

Необратимость времени в макроскопических процессах находит свое воплощение в законе возрастания энтропии. В обратимых процессах энтропия (мера внутренней неупорядоченности системы) остается постоянной, в необратимых — возрастает. Реальные же процессы всегда необратимы. В замкнутой системе максимально возможная энтропия соответствует наступлению в ней теплового равновесия: разности температур в отдельных частях системы исчезают и макроскопические процессы становятся невозможными. Вся присущая системе энергия превращается в энергию неупорядоченного, хаотического движения микрочастиц, и обратный переход тепла в работу невозможен.

Писатель-фантаст Р. Брэдбери в одной из своих повестей иллюстрирует свойство необратимости и однонаправленности