Нестандартные методы решения уравнений и неравенств

Не всякое уравнение или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению (неравенству) того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать другие методы решения, речь о которых и пойдет в ходе данной работы. Выше сказанное определяет актуальность курсовой работы. Объект исследования – уравнения и неравенства, не поддающиеся решению с помощью стандартных методов, или отличающиеся громоздкостью стандартного решения.

Целью данной работы является ознакомление с нестандартными методами решения уравнений и неравенств.

Для достижения поставленной цели в данной работе решались следующие задачи:

1. Собрать сведения из истории математики о решении уравнений.

2. Рассмотреть и применить на практике методы решения уравнений и неравенств, основанные на использовании свойств функции.

3. Рассмотреть и применить на практике дополнительные нестандартные методы решения уравнений и неравенств

Практическая значимость работы состоит в том, что не всегда при решении сложных уравнений или неравенств следует идти по «накатанной колее», пытаясь найти решение «в лоб»: достаточно лишь взглянуть на него и найти зацепку, позволяющую избежать сложных вычислений и преобразований. Курсовая работа состоит из введения, трех глав и списка использованных источников. В первой главе приведены некоторые сведения из истории математики о решении уравнений. Во второй главе рассмотрены методы решения, основанные на использовании свойств функции. Третья глава посвящена рассмотрению дополнительных (искусственных) методов решения.

1 ИСТОРИЧЕСКАЯ СПРАВКА

Уравнения и системы уравнений математики умели решать очень давно. В «Арифметике» греческого математика из Александрии Диофанта (III в.) еще не было систематического изложения алгебры, однако в ней содержался ряд задач, решаемых при помощи составления уравнений. Есть в ней такая задача:

«Найти два числа по их сумме 20 и произведению 96». (16)

Чтобы избежать решения квадратного уравнения общего вида, к которому приводит обозначение одного из чисел буквой и которое тогда еще не умели решать, Диофант обозначал неизвестные числа 10 + х и 10-х (в современной записи) и получал неполное квадратное уравнение 100-х² = 96, для которого указывал лишь положительный корень 2.

Задачи на квадратные уравнения встречаются в трудах индийских математиков уже с V в. н. э.

Квадратные уравнения классифицируются в трактате «Краткая книга об исчислении алгебры и алмукабалы» Мухаммеда аль-Хорезми (787 — ок. 850). В нем рассмотрены и решены (в геометрической форме) 6 видов квадратных уравнений, содержащих в обеих частях только члены с положительными коэффициентами. При этом рассматривались только положительные корни уравнений.

В работах европейских математиков XIII — XVI вв. даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов в общее правило произвел немецкий математик Михаэль Штифель (1487 — 1567), который рассматривал уже и отрицательные корни.

В самом известном российском учебнике «Арифметика» Леонтия Филипповича Магницкого (1669—1739) имелось немало задач на квадратные уравнения. Вот одна из них:

«Некий генерал хочет с 5000 человек баталию учинить, и чтобы та была в лице вдвое, нежели в стороне. Колико оная баталия будет иметь в лице и в стороне?», т. е. сколько солдат надо поставить по фронту и сколько им в затылок, чтобы число солдат по фронту было в 2 раза больше числа солдат, расположенных им «в затылок»?

В древневавилонских текстах (3000 — 2000 лет до н. э.) встречаются и задачи, решаемые теперь с помощью систем уравнений, содержащих и уравнения второй степени. Приведем одну из них:

«Площади двух своих квадратов я сложил: 25 . Сторона второго квадрата равна стороны первого и еще 5».

Соответствующая система в современной записи имеет вид:

Эту задачу вавилонский автор решает правильно методом, который мы теперь называем методом подстановки, но он еще не пользовался алгебраической символикой.

В XVI в. французский математик Франсуа Виет (1540 — 1603), служивший шифровальщиком при дворе французского короля, впервые ввел буквенные обозначения не только для неизвестных величин, но и для данных, т. е. коэффициентов уравнений. Ф. Виет для обозначения нерасшифрованных букв в донесениях противника использовал редкие буквы латинского алфавита х, у и z, что и положило начало традиции обозначать неизвестные в уравнениях буквами х, у и z. Особенно ценил Виет открытые им формулы, которые теперь называются формулами Виета. Однако сам Виет признавал только положительные корни.

Лишь в ХVII в. после работ Декарта, Ньютона и других математиков решение квадратных уравнений приняло современный вид.

Вернемся в начало XVI в. Тогда профессор математики болонского университета Сципион дель Ферро (1465—1526) впервые нашел алгебраическое решение уравнения третьей степени вида

x³+px=q, (1)

где р и q – числа положительные.

Это открытие, по обычаям того времени, профессор держал в строгом секрете. О нем знали лишь два его ученика, в том числе некий Фиоре. Утаивание математических открытий тогда было обычным явлением, так как в Италии практиковались математические диспуты-поединки. На многолюдных собраниях противники предлагали друг другу задачи для решения на месте или в определенный срок. Чаще всего это были задачи по алгебре, которую называли тогда великим искусством. Побеждал тот, кто решал больше задач. Победитель не только награждался славой и назначенным денежным призом, но и мог занять университетскую кафедру, а потерпевший поражение часто терял занимаемое место. Вот почему участнику диспута было важно обладать неизвестным другим алгоритмом решения некоторых задач.

После смерти профессора дель Ферро его ученик Фиоре, который сам не был глубоким математиком, вызвал на публичный диспут одного из виднейших математиков того времени Никколо Тарталья (1499—1557). Готовясь к диспуту, Тарталья открыл формулу для нахождения корней кубических уравнений в радикалах, так как предполагал, что Фиоре уже обладал этой формулой. Позднее Тарталья писал: «Я приложил все свое рвение, усердие и уменье, чтобы найти правило для решения кубических уравнений, и, благодаря благословенной судьбе, мне удалось это сделать за 8 дней до срока».

Диспут состоялся 20 февраля 1535 г. Тарталья в течение двух часов решил 30 задач, предложенных ему противником, а Фиоре не смог решить ни одной из 30 задач, предложенных Тартальей. После диспута Тарталья стал знаменитым во всей Италии, но продолжал держать открытую формулу в секрете.

Другой итальянский математик Джерол. но (1501 — 1576) узнал от Тартальи правило решения кубического уравнения (1) и дал «священную клятву», что никому не раскроет этой тайны. Правда, Тарталья лишь частично раскрыл свою тайну, но Кардано, познакомившись с рукописями покойного профессора дель Ферро, получил полную ясность в этом вопросе. В 1545 г. Кардано опубликовал знаменитый свой труд «О великом искусстве, или об алгебраических вещах, в одной книге», где впервые опубликовал формулу для решения уравнения (1), а кубическое уравнение общего вида предлагал свести к уравнению (1).

После выхода в свет этой книги Кардано был обвинен Тартальей в нарушении клятвы, но формула, открытая дель Ферро и Тартальей, и по сей день называется формулой Кардано.

Такова полная драматизма история открытия формулы корней кубического уравнения (1).

В той же книге Кардано привел алгебраическое решение уравнения четвертой степени. Это открытие сделал один из его учеников Лудовико Феррари (1522 — 1565). После этого начались настойчивые поиски формул, которые сводили бы решение уравнений высших степеней к извлечению корней («решение в радикалах»). Эти поиски продолжались около трех столетий, и лишь в начале XIX в. норвежский ученый Нильс Хенрик Абель (1802 —1829) и французский ученый Эварист Галуа (1811 —1832) доказали, что уравнения степеней выше четвертой в общем случае в радикалах не решаются.

Математик и философ Рене Декарт (1596 —1650) впервые сформулировал в своей книге «Геометрия» основную теорему алгебры о числе корней уравнения n-й степени. При этом Декарт допускал существование не только истинных (положительных) и ложных (меньших, чем ничего, т. е. меньших нуля — отрицательных) корней, но и воображаемых, мнимых (у Декарта — imaginaires), т. е. комплексных корней.

Еще в древности математики в процессе решения задач сталкивались с извлечением корня квадратного из отрицательного числа; в этом случае задача считалась неразрешимой. Однако постепенно выяснялось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a + bi, где i² = -1, которые в конце концов тоже стали называть числами, но уже комплексными. Первое обоснование простейших действий над комплексными числами дал итальянский математик Раффаэле Бомбелли (ок. 1530 —1572) в 1572 г., хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному.

Академик Петербургской академии наук Леонард Эйлер (1707 —1783) внес существенный вклад в вопросы теории комплексных чисел. После его работ комплексные числа получили окончательное признание как предмет и средство изучения. Само название «комплексное число» было предложено в 1831 г. немецким математиком Карлом Фридрихом Гауссом (1777 — 1855).

В настоящее время комплексные числа широко употребляются во многих вопросах физики и техники.

Выше речь шла об алгебраических уравнениях, т. е. уравнениях f(x) = O, где f(x) — многочлен относительно х.

Кроме алгебраических уравнений, есть еще и трансцендентные уравнения: показательные, логарифмические, тригонометрические и др. Решение трансцендентных уравнений, а также неравенств существенно опирается на свойства функций, которые изучаются в математике относительно недавно.

Особое место среди алгебраических уравнений занимают так называемые диофантовы уравнения, т. е. уравнения, в которых неизвестных больше одной.

Наиболее известными из них являются линейные диофантовы уравнения. Примеры задач, приводящих к линейным диофантовым уравнениям, находим в сборнике задач монаха Алькуина, приглашенного в 795 г. Карлом Великим преподавать в первую из известных школ в г. Аахен. Вот эта задача:

«100 шеффелей (денежных единиц) разделили между мужчинами, женщинами и детьми (число персон 100) и дали при этом мужчинам по 3 шеффеля, женщинам по 2 и детям по шеффеля. Сколько было мужчин, женщин и детей?»

Обозначив количество мужчин за х, количество женщин за у, мы придем к уравнению

Зх + 2y+ (100-х-y)= 100

Общего решения линейных диофантовых уравнений в те времена еще не знали и довольствовались лишь несколькими решениями, удовлетворяющими условию задачи. У самого Алькуина было приведено лишь одно решение этой задачи: мужчин, женщин и детей было 11, 15 и 74, а задача имеет 784 решения в натуральных числах.

Задачи, приводящие к линейным диофантовым уравнениям, имелись у Леонардо Пизанского (Фибоначчи) (1180 — 1240), в «Арифметике» Л. Ф. Магницкого.

Известное диофантово уравнение Пифагора (VI в. до н. э.) х² + у²= z² решают в натуральных числах. Его решениями служат тройки чисел (х; у; z):

x = (m²-n²)l, y = 2mnl, z = (m² + n²)l,

где т, п, l - любые натуральные числа (т> п). Эти формулы помогают находить прямоугольные треугольники, длины сторон которых являются натуральными числами.

В 1630 г. французский математик Пьер Ферма (1601 — 1665) сформулировал гипотезу, которую называют великой (или большой) теоремой Ферма: «Уравнение х^п + у^п = zⁿ для натурального п ≥ 3 не имеет решений в натуральных числах». Ферма не доказал свою теорему в общем случае, но известна его запись на полях «Арифметики» Диофанта: «...невозможно куб записать в виде суммы двух кубов, или четную степень в виде суммы таких же степеней, или вообще любое число, которое является степенью большей, чем вторая, нельзя записать в виде суммы двух таких же степеней. У меня есть поистине удивительное доказательство этого утверждения, но поля эти слишком узки, чтобы его уместить». Позднее в бумагах Ферма было найдено доказательство его теоремы для п= 4. С тех пор более 300 лет математики пытались доказать великую теорему Ферма. В 1770 г. Л.Эйлер доказал теорему Ферма для п = 3, в 1825 г. Адриен Лежандр (1752 1833) и Петер Дирихле (1805 — 1859) — для п = 5. Доказательство великой теоремы Ферма в общем случае не удавалось долгие годы. И только в 1995 г. Эндрю Вайлс доказал эту теорему.

2. РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ ФУНКЦИИ

Не всякое уравнение f(x) = g(x) или неравенство в результате преобразований или с помощью удачной замены переменной может быть сведено к уравнению или неравенству того или иного стандартного вида, для которого существует определенный алгоритм решения. В таких случаях иногда оказывается полезным использовать некоторые свойства функций, такие как монотонность, периодичность, ограниченность, четность и др.

2.1 Использование монотонности функции

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) < f (x₂).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) > f (x₂).

На показанном на рисунке 1 графике

Рисунок 1

Функция y = f (x), , возрастает на каждом из промежутков (a; x₁) и (x₂; b) и убывает на промежутке (x₁; x₂). Обратите внимание, что функция возрастает на каждом из промежутков (a; x₁) и (x₂; b), но не на объединении промежутков

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ < x₂ – корни этого уравнения на промежутке D (f(x)), то f (x₁) = f (x₂) = 0, что противоречит условию монотонности.

Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).

· Сумма нескольких возрастающих функций является возрастающей функцией.

· Произведение неотрицательных возрастающих функций есть возрастающая функция.

· Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.

· Если функция f возрастает и сохраняет знак, то функция убывает.

· Если функция f возрастает и неотрицательна, то fⁿ где nN, также возрастает.

· Если функция f возрастает и n – нечетное число, то fⁿ также возрастает.

· Композиция g (f (x)) возрастающих функций f и g также возрастает.

Аналогичные утверждения можно сформулировать и для убывающей функции.

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого (x ≠ a) выполняется неравенство f (x) ≤ f (a) , то точка a называется точкой наибольшего значения функции на множестве D:

Если для любого (x ≠ b) выполняется неравенство f (x) > f (b) , то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения функции на множестве D может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

Решение уравнений и неравенств с использованием свойства монотонности основывается на следующих утверждениях.

1. Пусть f(х) — непрерывная и строго монотонная функция на промежутке Т , тогда уравнение f(x) = С, где С — данная константа, может иметь не более одного решения на промежутке Т.

2. Пусть f(x) и g(х) — непрерывные на промежутке T функции, f(x) строго возрастает, а g(х) строго убывает на этом промежутке, тогда уравнение f(х) = =g(х) может иметь не более одного решения на промежутке Т. Отметим, что в качестве промежутка T могут быть бесконечный промежуток (-∞;+∞) , промежутки (а;+∞), (-∞; а), (а;+∞), (-∞; b), отрезки, интервалы и полуинтервалы.

Пример 2.1.1 Решите уравнение

. (28) (1)

Решение. Очевидно, что х ≤ 0 не может являться решением данного уравнения, так как тогда . Для х > 0 функция непрерывна и строго возрастает, как произведение двух непрерывных положительных строго возрастающих для этих х функций f(x) = х и . Значит, в области х > 0 функция принимает каждое свое значение ровно в одной точке. Легко видеть, что х = 1 является решением данного уравнения, следовательно, это его единственное решение.

Ответ: {1}.

Пример 2.1.2Решите неравенство

. (2)

Решение. Каждая из функций у = 2^x, у = 3^x, у = 4^х непрерывная и строго возрастающая на всей оси. Значит, такой же является и исходная функция . Легко видеть, что при х = 0 функция принимает значение 3. В силу непрерывности и строгой монотонности этой функции при х > 0 имеем , при х < 0 имеем . Следовательно, решениями данного неравенства являются все х < 0.

Ответ: (-∞; 0).

Пример 2.1.3 Решите уравнение

. (3)

Решение. Область допустимых значений уравнения (3) есть промежуток . На ОДЗ функции и непрерывны и строго убывают, следовательно, непрерывна и убывает функция . Поэтому каждое свое значение функция h(x) принимает только в одной точке. Так как , то х = 2 является единственным корнем исходного уравнения.

Ответ: {2}.

2.2 Использование ограниченности функции

При решении уравнений и неравенств свойство ограниченности снизу или сверху функции на некотором множестве часто играет определяющую роль.

Если существует число C такое, что для любого выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D (рисунок 2).

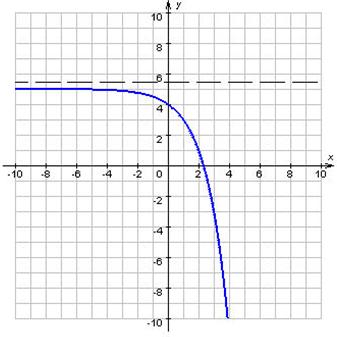
Рисунок 2

Если существует число c такое, что для любого выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D (рисунок 3).

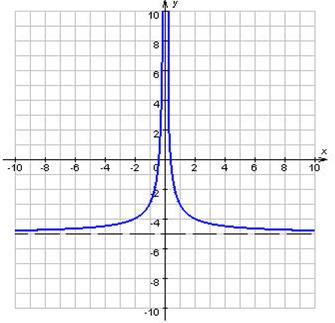
Рисунок 3

Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), лежит в полосе c ≤ y ≤ C (рисунок 4).

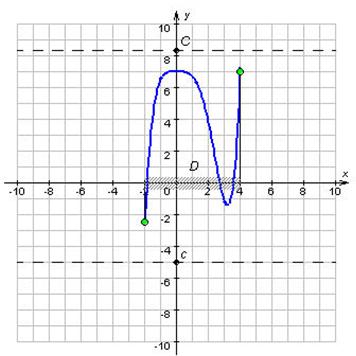
Рисунок 4

Если функция не является ограниченной на множестве, то говорят, что она не ограничена.

Примером функции, ограниченной снизу на всей числовой оси, является функция y = x². Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = 1/x. Примером функции, ограниченной на всей числовой оси, является функция y = sin x.

Пример 2.2.1 Решите уравнение

sin(x³ + 2х² + 1) = х² + 2х + 2. (4)

Решение. Для любого действительного числа х имеем sin(x³ + 2х² + 1) ≤ 1, х² + 2х + 2 = (x + 1)²+ 1 ≥ 1. Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда не меньше единицы, то данное уравнение может иметь решение только при .

При , , т.е. при уравнение (4) так же корней не имеет .

Ответ: Ø.

Пример 2.2.2 Решите уравнение

. (5)

Решение. Очевидно, что х = 0, х = 1, х = -1 являются решениями данного уравнения. Для нахождения других решений в силу нечетности функции f(х) = = x³ - x - sin πx достаточно найти его решения в области х > 0, х ≠ 1, поскольку если x₀ > 0 является его решением, то и (-x₀) также является его решением.

Разобьем множество х > 0, х ≠ 1, на два промежутка: (0; 1) и (1; +∞)

Перепишем начальное уравнение в виде x³ - x = sin πx. На промежутке (0; 1) функция g(х) = x³ - x принимает только отрицательные значения, поскольку х³ < < х, а функция h(x) = sin πx только положительные. Следовательно, на этом промежутке уравнение не имеет решений.

Пусть х принадлежит промежутку (1; +∞). Для каждого из таких значений х функция g(х) = х³ - х принимает положительные значения, функция h(x) = sin πx принимает значения разных знаков, причем на промежутке (1; 2) функция h(x) = sin πx неположительна. Следовательно, на промежутке (1; 2) уравнение решений не имеет.

Если же х > 2, то |sin πx| ≤ 1, x³ - x = x(x² - 1) > 2∙3 = 6, а это означает, что и на промежутке (1; +∞) уравнение также не имеет решений.

Итак, x = 0, x = 1 и x = -1 и только они являются решениями исходного уравнения.

Ответ: {-1; 0; 1}.

Пример 2.2.3 Решите неравенство

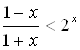. (6)

Решение. ОДЗ неравенства есть все действительные x, кроме x = -1. Разобьем ОДЗ неравенства на три множества: -∞ < x < -1, -1 < x ≤ 0, 0 < x < +∞ и рассмотрим неравенство на каждом из этих промежутков.

Пусть -∞ < x < -1. Для каждого из этих x имеем g(x) = < 0, а f(x) = 2^x > 0. Следовательно, все эти x являются решениями неравенства.

Пусть -1 < x ≤ 0. Для каждого из этих x имеем g(x) = 1 - , а f(x) = 2^x≤ 1. Следовательно, ни одно из этих x не является решением данного неравенства.

Пусть 0 < x < +∞. Для каждого из этих x имеем g(x) = 1 - , a . Следовательно, все эти x являются решениями исходного неравенства.

Ответ: .

2.3 Использование периодичности функции

Функция f (x) называется периодической с периодом T ≠ 0, если выполняются два условия:

· если , то x + T и x – T также принадлежат области определения D (f (x));

· для любого выполнено равенство

f (x + T) = f (x).

Поскольку то из приведенного определения следует, что

Если T – период функции f (x), то очевидно, что каждое число nT, где , n ≠ 0, также является периодом этой функции.

Наименьшим положительным периодом функции называется наименьшее из положительных чисел T, являющихся периодом данной функции.

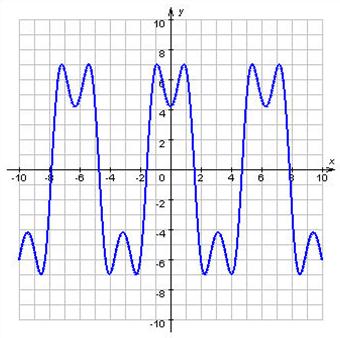
График периодической функции

График периодической функции обычно строят на промежутке (x₀; x₀ + T), а затем повторяют на всю область определения.

Хорошим примером периодических функций могут служить тригонометрические функции y = sin x, y = cos x (период этих функций равен 2π), y = tg x (период равен π) и другие. Функция y = const также является периодической. Для нее периодом является любое число T ≠ 0.

В заключение отметим свойства периодических функций. (19)

· Если f (x) – периодическая функция с периодом T, то функция

g (x) = A · f (kx + b)

где k ≠ 0 также является периодической с периодом .

· Пусть функции f₁ (x) и f₂ (x) определены на всей числовой оси и являются периодическими с периодами T₁ > 0 и T₂ > 0. Тогда если то функция периодическая с периодом T, равным наименьшему общему кратному чисел T₁и T_2.