Некоторые уравнения математической физики в частных производных

Глава 1. Уравнения гиперболического типа

1.1 Задачи, приводящие к уравнениям гиперболического типа

1.2 Уравнение колебаний струны

1.3 Метод разделения переменных. Уравнение свободных колебаний струны

1.4 Решение уравнений

Глава 2. Уравнения параболического типа

2.1 Уравнение распространения тепла в стержне

2.2 Решение задач

Заключение

Литература

2.1 Уравнение распространения тепла в стержне

Рассмотрим однородный стержень длины . Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .

Рис. 2.1.

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

(1)

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = х). Количество тепла, прошедшего через сечение с абсциссой х1 за время t, будет равно

 (2)

то же самое с абсциссой х2:

 (3)

Приток Q1 - Q2 в элемент стержня за время t будет равняться:

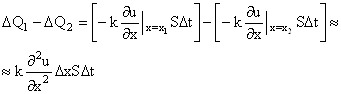 (4)

Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:

Или

 (5)

где с – теплоемкость вещества стержня,  – плотность вещества стержня (xS – масса элемента стержня).

Приравнивая выражения (4) и (5) одного и того же количества тепла , получим:

(6)