Квантование сообщений. Ошибки квантования. Энтропия источника сообщений

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

кафедра РЭС

реферат на тему:

"Квантование сообщений. Ошибки квантования. Энтропия источника сообщений"

МИНСК, 2009

Квантование сообщений. Ошибки квантования

Итак, показано, что передачу практически любых сообщений λ(t) ({λ(x,y) }) можно свести к передаче их отсчетов, или чисел λi = λ(i Dt), следующих друг за другом с интервалом дискретности Dt £ 1/2Fm (Δx ≤ 1/2fx, Δy ≤ 1/2fy). Тем самым непрерывное (бесконечное) множество возможных значений сообщения λ(t) заменяется конечным числом его дискретных значений {λ(i Dt) }. Однако сами эти числа имеют непрерывную шкалу уровней (значений), то есть принадлежат опять же континуальному множеству. Для абсолютно точного представления таких чисел, к примеру, в десятичной (или двоичной) форме, необходимо теоретически бесконечное число разрядов. Вместе с тем на практике нет необходимости в абсолютно точном представлении значений λi, как и любых чисел вообще.

Во-первых, сами источники сообщений обладают ограниченным динамическим диапазоном и вырабатывают исходные сообщения с определенным уровнем искажений и ошибок. Этот уровень может быть большим или меньшим, но абсолютной точности воспроизведения достичь невозможно.

Во-вторых, передача сообщений по каналам связи всегда производится в присутствии различного рода помех. Поэтому принятое (воспроизведенное) сообщение (оценка сообщения l*(t) или L*) всегда в определенной степени отличается от переданного, то есть на практике невозможна абсолютно точная передача сообщений при наличии помех в канале связи.

Наконец, сообщения передаются для их восприятия и использования получателем. Получатели же информации - органы чувств человека, исполнительные механизмы и т.д. - также обладают конечной разрешающей способностью, то есть не замечают незначительной разницы между абсолютно точным и приближенным значениями воспроизводимого сообщения. Порог чувствительности к искажениям также может быть различным, но он всегда есть.

С учетом этих замечаний процедуру дискретизации сообщений можно продолжить, а именно подвергнуть отсчеты λi квантованию.

Процесс квантования состоит в замене непрерывного множества значений отсчетов li Î (lmin, lmax) дискретным множеством { l(1),...,l(m) } из алфавита A{ λi }. Тем самым точные значения чисел li заменяются их приблизительными (округленными до ближайшего разрешенного уровня) значениями. Интервал между соседними разрешенными уровнями li, или уровнями квантования, D = l(i+1) - l(i) называется шагом квантования.

Различают равномерное и неравномерное квантование. В большинстве случаев применяется и далее подробно рассматривается равномерное квантование (рис.1), при котором шаг квантования постоянный: D = λi - λi-1 = = const; однако иногда определенное преимущество дает неравномерное квантование, при котором шаг квантования Di разный для различных λi (рис.2).

Рис. 1. Рис. 2.

Квантование приводит к искажению сообщений. Если квантованное сообщение, полученное в результате квантования отсчета li = l(iΔt), обозначить как λiq, то

(1)

где xi - разность между квантованным сообщением (ближайшим разрешенным уровнем) λiq и истинным значением элементарного сообщения li, называемая ошибкой квантования, или шумом квантования. Шум квантования оказывает на процесс передачи информации по существу такое же влияние, как и помехи в канале связи. Помехи, так же как и квантование, приводят к тому, что оценки λ*i, получаемые на приемной стороне системы связи, отличаются на некоторую величину от истинного значения li.

Поскольку квантование сообщений приводит к появлению ошибок и потере некоторой части информации, можно определить цену таких потерь d(l, λq) и среднюю величину ошибки, обусловленной квантованием:

(2)

Чаще всего в качестве функции потерь (цены потерь) используется квадратичная функция вида

(3)

В этом случае мерой ошибок квантования служит дисперсия этих ошибок. Для равномерного N-уровневого квантования с шагом D дисперсия ошибок квантования определяется следующим образом:

. (4)

Абсолютное значение ошибки квантования не превосходит половины шага квантования D/2, и тогда при достаточно большом числе уровней квантования N и малой величине D плотность распределения вероятностей ошибок квантования f(xi) можно считать равномерной на интервале +D/2 … - D/2:

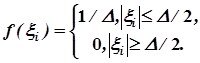(5)

В результате величина ошибки квантования D(q) = σq2 определится соотношением

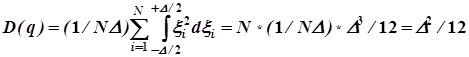(6)

и соответствующим выбором шага квантования D может быть сделана сколь угодно малой или сведена к любой наперед заданной величине.

Относительно требуемой точности передачи отсчетов сообщений можно высказать те же соображения, что и для ошибок временной дискретизации: шумы квантования или искажения, обусловленные квантованием, не имеют существенного значения, если эти искажения меньше ошибок, обусловленных помехами и допустимых техническими условиями.

Так, например, при передаче речи и музыки искажения практически не заметны, если все отсчеты случайным образом изменить на 0,1…1%, при передаче изображений - на 1% и т.д. Даже профессиональный эксперт не может заметить искажений в музыкальном произведении, если квантование производится с точностью лучше 0,001% (число уровней квантования N > 100000, точность представления отсчетов - 16…17 двоичных разрядов). Число уровней квантования сообщений в телеметрических системах зависит от требуемой точности воспроизведения информации, а также от точности датчиков, осуществляющих сбор этой информации. При этом превышение при квантовании достижимой датчиками или требуемой точности нецелесообразно из-за увеличения сложности аппаратуры и затрат на передачу. Более того, при передаче по каналу связи с помехами могут возникать ситуации, когда качество воспроизведения оценки сообщения λ*i при более грубом его квантовании на передающей стороне оказывается значительно лучшим, чем для точного квантования. На этом достаточно неочевидном, но вытекающем из общей теории передачи информации явлении в дальнейшем более подробно остановимся.

Таким образом, показано, что передачу практически любых сообщений λ(t) ({λ(x,y) }) с любой наперед заданной точностью можно свести к передаче целых чисел λiq = λq(i Dt), следующих друг за другом с интервалом дискретности Dt £ 1/2Fm (Δx ≤ 1/2fx max, Δy ≤ 1/2fy max). Тем самым непрерывное (бесконечное) множество возможных значений сообщения λ(t) ({λ(x,y) }) заменяется конечным множеством целых чисел из алфавита A{ λi q }, (i =1,2…N). Иными словами, теперь можно работать с сигналами, как с числами, а это позволяет применять для их обработки и анализа цифровые алгоритмы любой степени сложности, практически нереализуемые в аналоговой форме, использовать в системах передачи информации цифровые методы и современные цифровые интегральные технологии и т.д.

Итак, мы выяснили, что в радиотехнических системах носителями или переносчиками информации являются электрические сигналы, формируемые источниками этой информации. Даже в тех случаях, когда первичная информация носит неэлектрическую природу (речь, музыка, изображения, тексты, пакеты данных и т.д.), она в конечном итоге преобразуется в электрические сигналы и далее сохраняется или передается по каналам связи. Эти сигналы обычно носят непрерывный характер, то есть определены для любого момента времени или в бесконечном числе точек своего существования. Гораздо удобнее иметь дело с данными, имеющими конечный размер, – например, с массивами чисел конечного размера и ограниченной разрядности. Рассмотренная выше теорема дискретизации дает такую возможность.

Количество информации, энтропия источника сообщений

Для сравнения между собой различных источников сообщений необходимо ввести некоторую количественную меру, которая дала бы возможность объективно оценить информацию, содержащуюся в сообщении. Такая мера впервые была введена K. Шенноном в 1948 г., а затем более строго определена А.Я. Хинчиным. Рассмотрим основы информационного подхода Шеннона.

Всякая информация получается потребителем после приема сообщения, то есть в результате опыта. Сообщение, получаемое на приемной стороне, несет полезную информацию лишь в том случае, если имеется неопределенность относительно состояния источника. Если опыт может закончиться только одним исходом и наблюдатель заранее знает исход опыта, то по его результату он не получает никакой информации. Например, если сообщат, что солнце всходит на востоке, то никакой информации это сообщение не принесет, поскольку все знают, что это верно. В таком событии, как ежедневный восход солнца на востоке, нет ничего неопределенного, вероятность этого события равна единице и количество информации, приносимое сообщением о таком событии, равно нулю. Информация появится лишь тогда, когда источник будет иметь по крайней мере более одного возможного состояния.

Рассмотрим источник, выдающий последовательность независимых дискретных сообщений {li}, каждое из которых случайным образом выбирают из алфавита сообщения A (li) = l1, l2, l3,... lK, где K - размер алфавита источника. Такой источник будем называть источником без памяти с конечным дискретным алфавитом. Сообщения, вырабатываемые таким источником, называются простыми сообщениями.

В каждом элементарном сообщении li для его получателя содержится некоторая информация. Определим количественную меру этой информации и выясним, от чего она зависит.

До того, как связь состоялась, у получателя всегда имеется большая или меньшая неопределенность относительно того, какое сообщение li из числа возможных будет передано.

Совершенно очевидно, что степень этой неопределенности, или неожиданности передачи li, зависит от вероятности передачи того или иного сообщения. Например, если вероятность передачи какого-либо сообщения li очень высока, то еще до передачи мы почти наверняка знаем, какое сообщение будет передано, и его прием не принесет нам почти никакой новой информации.

Таким образом, очевидно, что количество информации, содержащейся в элементарном сообщении li, является некоторой функцией от вероятности передачи этого сообщения Р(li):

J (li) = j {P (li) }. (7)

Определим вид этой функции j. Для этого потребуем, чтобы мера количества информации J(li) удовлетворяла двум интуитивным свойствам:

1. Если выбор сообщения li заранее предопределен (Р(li) = 1 - неопределенности нет), то количество информации в этом сообщении равно нулю: J (li) = j {1} = 0.

2. Если источник последовательно выбирает сообщения li и lj и вероятность такого выбора Р(li, lj) есть совместная вероятность событий li и lj, то количество информации в этих двух элементарных сообщениях будет равно сумме количеств информации в каждом из них.

Вероятность совместного выпадения событий li и lj Р(li, lj), как известно, определяется по формуле полной вероятности

Р (li, lj) = Р(li) × Р(lj /li) = P × Q. (8)

Тогда, в соответствии с требованием (2), должно выполняться условие

j { P× Q } = j (P) + j (Q). (9)

Нетрудно догадаться, что функцией, удовлетворяющей этим двум предъявляемым к ней условиям, является функция вида

J (li) = a log P(li), (10)

при этом как коэффициент a, так и основание логарифма могут быть выбраны произвольно. Однако для удобства (чтобы количественная мера информации была положительной) принимают a = - 1. Основание логарифма обычно выбирают равным двум, и тогда

J (li) = - log2 P(li). (11)

Определенная таким образом единица измерения информации называется двоичной единицей, или битом информации. Например, если какое-либо из элементарных сообщений li может быть выбрано из алфавита и передано с вероятностью P(li) = 1/8, то говорят, что в нем содержится log2 (1/8) = 3 бита информации.

Иногда в качестве основания логарифма выбирают e, тогда информация измеряется в натуральных единицах, или натах.

Количество информации, содержащееся в одном элементарном сообщении li, еще никак не характеризует источник. Одни элементарные сообщения могут нести много информации, но передаваться очень редко, другие - передаваться чаще, но нести меньше информации. Поэтому источник может быть охарактеризован средним количеством информации, приходящимся на одно элементарное сообщение, носящим название “энтропия источника” и определяемым следующим образом:

, i = 1, K. (12)

Энтропия, как количественная мера информативности источника, обладает следующими свойствами:

1. Энтропия есть величина вещественная, ограниченная и неотрицательная. Эти ее свойства вытекают из вида выражения для Н(l), а также с учетом того, что 0 < P(li) < 1.

2. Энтропия детерминированных сообщений равна нулю, то есть Н(l) = 0, если хотя бы одно из сообщений имеет вероятность, равную единице.

3. Энтропия максимальна, если сообщения li равновероятны, то есть

P(l1) = P(l2) =... ... . P(lk) = 1/K, и тогда

(13)

Как видно из последнего выражения, в случае равновероятных сообщений энтропия растет с увеличением объема алфавита источника (ростом числа сообщений). При неравновероятных элементарных сообщениях li энтропия, соответственно, уменьшается.

4. Энтропия двоичного источника (K = 2) может изменяться от нуля до единицы. Действительно, энтропия системы из двух сообщений l1 и l2

(14)

Из последнего выражения видно, что энтропия равна нулю при P(l1) = 0; P(l2) =1, или P(l1) = 1; P(l2) = 0; при этом максимум энтропии будет иметь место, когда P(l1) =P(l2) =1/2 и ее максимальное значение будет равно 1 бит.

ЛИТЕРАТУРА

1. Лидовский В.И. Теория информации. - М., "Высшая школа", 2002г. – 120с.

2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И. Нефедов, В.И. Халкин, Е.В. Федоров и др. – М.: Высшая школа, 2001 г. – 383с.

3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.

4. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. М: Радио и связь, 2001 г. –368 с.

5. Б. Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд.2-е, испр.: Пер. с англ. – М.: Издательский дом "Вильямс", 2003 г. – 1104 с.