Управление динамической системой
1. Исходные данные
2. Нахождение аналитического вида функций Mc(ω) и Mg(ω,μ)
3. Нахождение равновесного состояния системы
4. Численное нахождение функций ω(t) и μ(t) равновесного состояния
5. Линеаризация и численное решение разомкнутой системы
6. Замкнутая система
7. Оценка управляемости системы
8. Оценка устойчивости системы
9 Построение переходного процесса
10. Нахождение передаточной функции для разомкнутой системы
11. Амплитудная, фазовая, вещественная, мнимая и амплитудно-фазовая частотные характеристики
12. Оценка устойчивости системы по критерию Найквиста, по критерию Михайлова
Заключение
Библиографический список
Введение
Теория управления – это наука, изучающая процессы в системах управления с информационной точки зрения, обычно абстрагируясь от физической природы объектов и управляющих устройств. Процессы в автоматических системах управления изучает теория автоматического управления.
Важнейшие принципы построения систем автоматического управления:
· принцип обратной связи;
· принцип оптимальности;
· принцип адаптивности;
· принцип робастности.
По степени использования информации об объекте различают разомкнутые и замкнутые системы управления. При разомкнутом управлении воздействие на объект осуществляется по заданной программе вне зависимости от результатов управления в предыдущий период времени. Замкнутые системы управления используют информацию о результатах управления и формируют управляющее воздействие в зависимости от того, насколько достигается цель управления.
1 Исходные данные
Динамика объекта управления описывается следующей системой дифференциальных уравнений
а) Уравнение моментов:
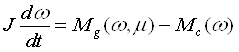(1)
б) Уравнение управляющего устройства:
t - время, сек; J - момент инерции движущихся частей, приведенный к валу двигателя, кг*м / сек2; w - угловая скорость двигателя, 1/сек; Mg, Mc - момент движущих сил и сил сопротивления, кг*м; m - управляющее воздействие; u - задающее воздействие; 
, 
- параметры управляющего устройства
Функции Mg, Mc заданы таблицами 1 и 2, численные значения коэффициентов определены в таблице 3
Таблица 1 – Зависимость Mg от w и m
| w | m | |||||
| 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
| 0.00 | 53.50 | 55.62 | 57.54 | 59.86 | 61.98 | 64.10 |
| 10.60 | 46.28 | 48.63 | 50.99 | 53.35 | 55.71 | 58.06 |
| 21.20 | 36.48 | 39.08 | 41.67 | 44.27 | 46.86 | 49.46 |
| 31.80 | 24.11 | 26.95 | 29.78 | 32.61 | 35.44 | 38.27 |
| 42.40 | 9.17 | 12.24 | 15.31 | 18.38 | 21.45 | 24.52 |
| 53.00 | 0.00 | 0.00 | 0.00 | 1.58 | 4.89 | 8.19 |
Таблица 2 – Зависимость Mс от w
| w | 0.00 | 10.60 | 21.20 | 31.80 | 42.40 | 53.00 |
| Мс | 10.70 | 13.50 | 20.22 | 30.84 | 45.37 | 63.82 |
Таблица 3 – Значение параметров системы
| J | m | R1 | R2 | C |
| 0.06 | 10.03 | 19.40 | 1.03 | 1.03 |
Начальные условия: t = 0; w = 0; m = 0; 
; u = 0.5.(3)
2 Нахождение аналитического вида функций Mc(ω) и Mg(ω,μ)
динамическая система (1)
Аналитический вид функции момента движущих сил Mc(ω) находится методом наименьших квадратов:
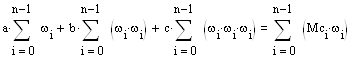
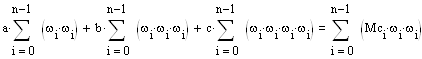
Аналитический вид функции момента движущих сил Mg(ω,μ) находится методом наименьших квадратов. Сначала по столбцам при различных μ вычисляется матрица ABC зависимости Mg(ω,μ) от μ. Первый столбец матрицы ABC вычисляется при μ=0 из системы:
|
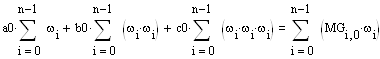
