Аксиоматика векторного пространства

Глава 2

1. Некоторые векторные равенства

Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные соотношения являются, образно выражаясь, ключами к решению широкого класса задач.

I Основное соотношение. Во всяком треугольнике ЛВС выполняется равенство

(I)

Где М – центроид (точка пересечения медиан) треугольника АВС.

Докажем соотношение (I).

Пусть М – центроид треугольника АВС. Соединим точку М со всеми вершинами треугольника. Прямая МВ пересекает сторону АС треугольника АВС в точке О, являющейся серединой стороны АС. На прямой ВМ откладываем МЕ = ВМ и соединяем точку Е с вершинами А и С. очевидно, что АМСЕ –параллелограмм. Поэтому . Откуда . Так как , то . Ч.т.д.

Задача. Доказать, что если М – центроид треугольника АВС и О -произвольная точка пространства, то выполняется равенство

(1)

Доказательство:

Запишем следующие векторные равенства:

Сложив эти равенства по частям, получаем:

,

откуда

Доказанное равенство также следует отнести к основным векторным соотношениям, так как оно часто используется в решении многих задач.

II Основное соотношения. В треугольнике АВС на стороне АС взята точка D так, что АD : DС = m: .

Тогда имеет месть следующее соотношение:

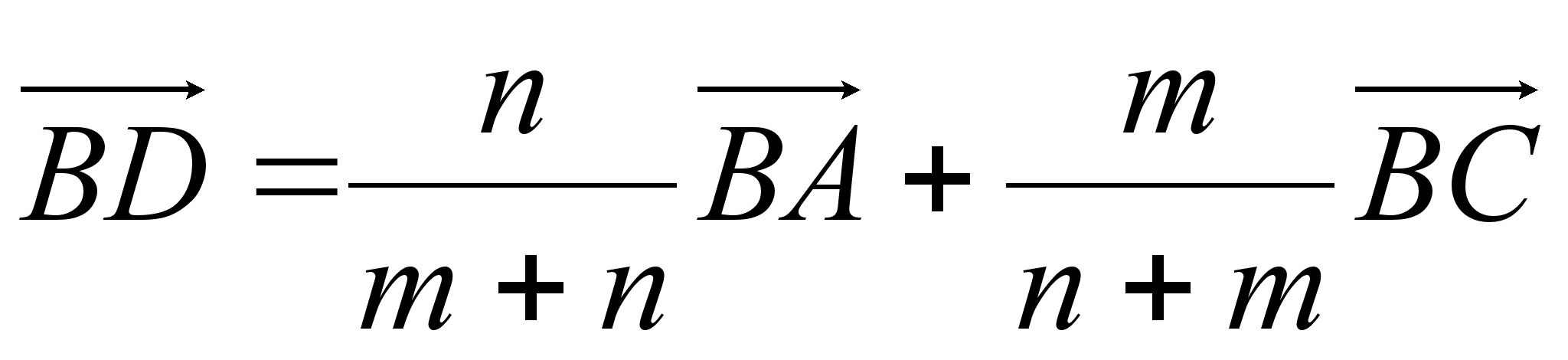(II)

Доказательство:

Из треугольника АВС имеем:

.

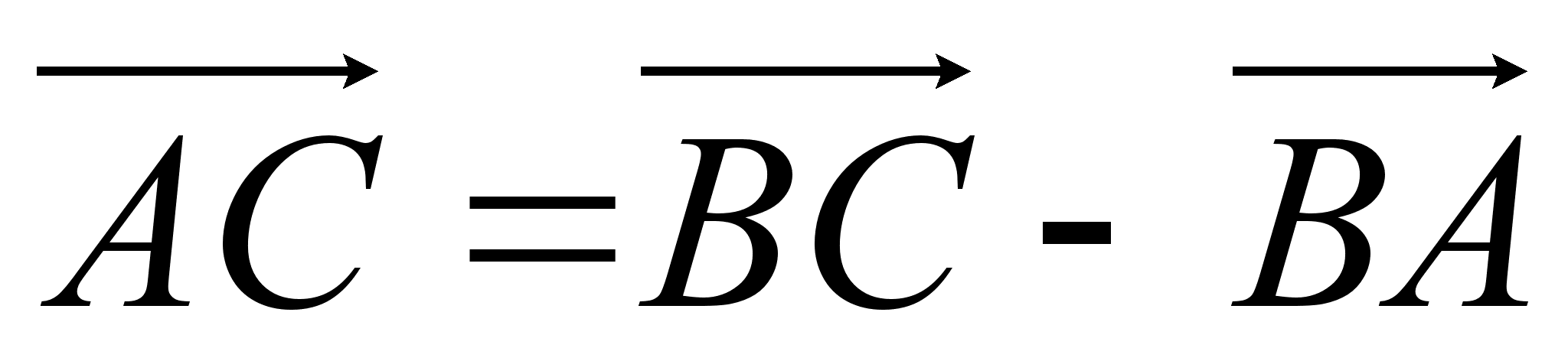
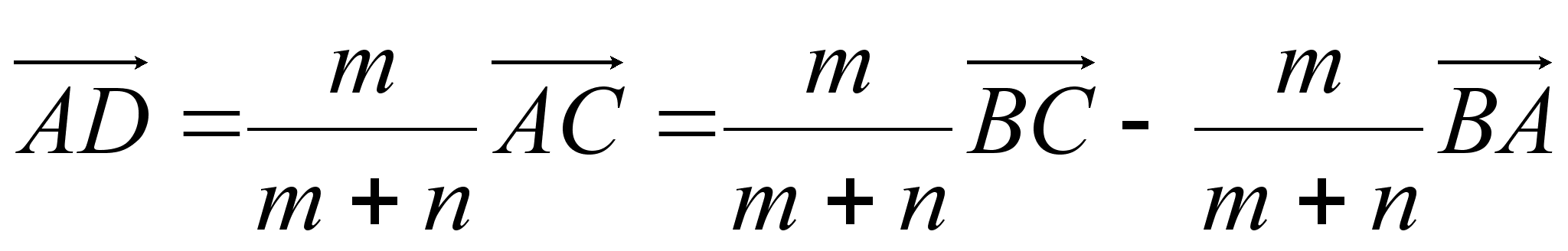
Ч.т.д.

Задача. Через середину Е медианы СС₁ треугольника АВС проведена прямая АЕ, пересекающая сторону ВС в точке F. Вычислить АЕ : ЕF и СF : FВ.

Решение.

Введем векторы и . Пусть СF : FВ = m : . Тогда по формуле (II) имеем:

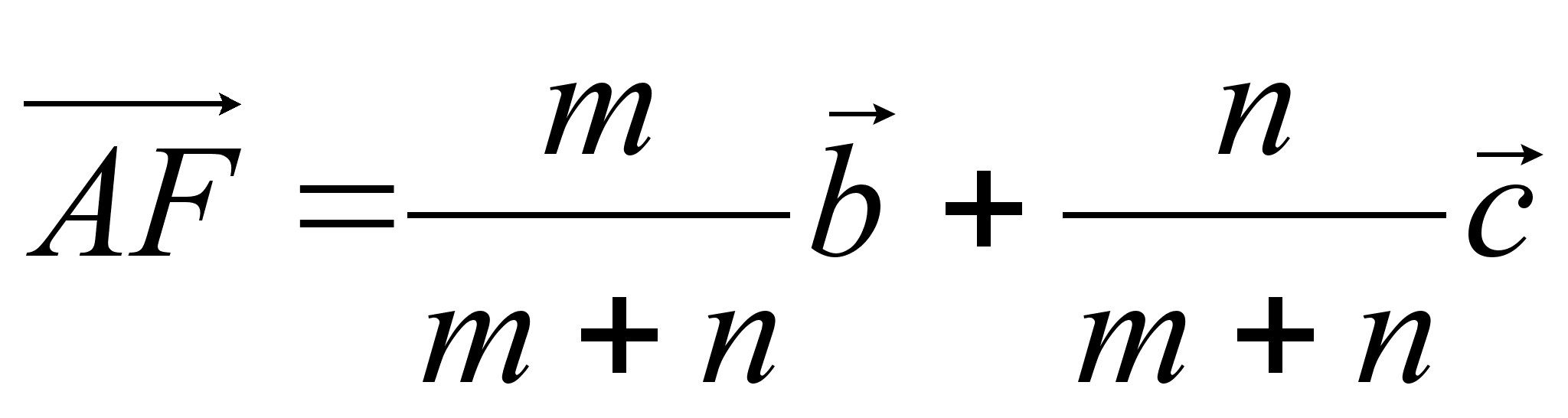
и 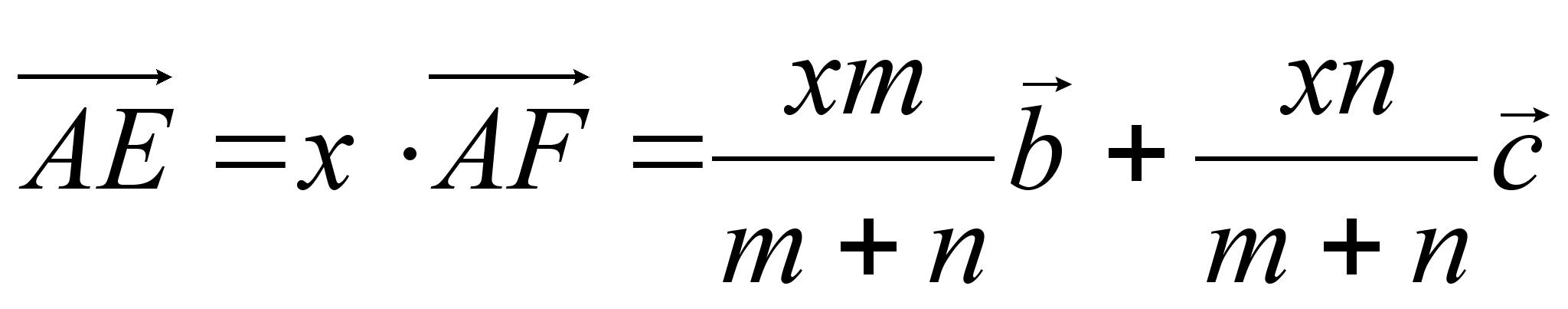(1)

где 0 < х< 1.

С другой стороны, учитывая, что Е – середина медианы СС₁ получаем для АЕ следующее выражение:

(2)

В силу единственности разложения вектора по двум векторам из (1) и (2) получаем систему:

(3)

Разделив по частям первое уравнение системы (3) на второе, получаем, что m : = 1 : 2, т.е. СF : FВ = 1 : 2.

Сложив по частям уравнение системы (3), находим, что 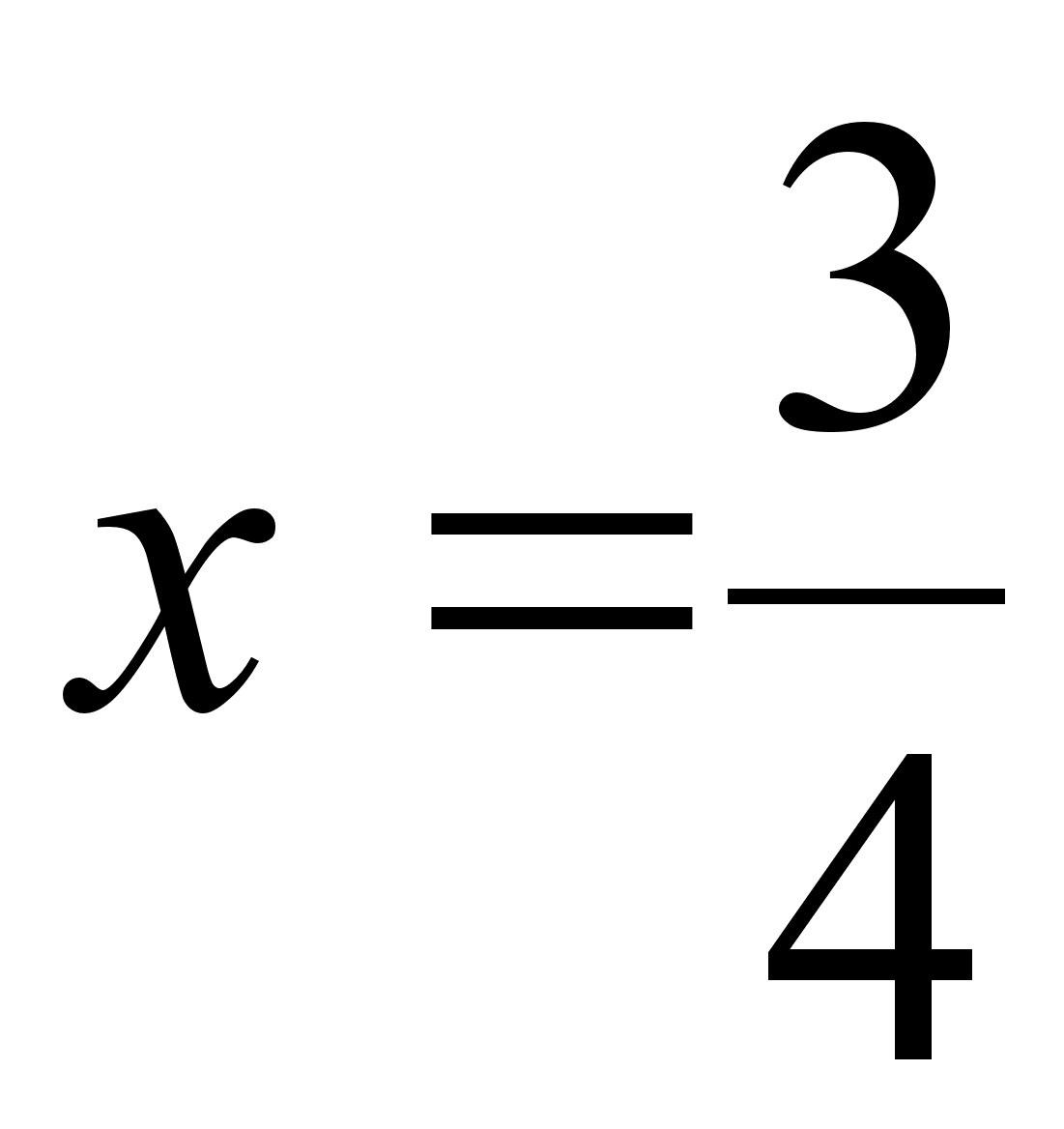, т.е. AE : EF = 3 : 4

I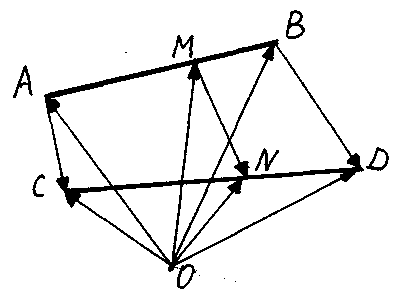II Основное соотношение. Если точки М и N делят отрезки АВ и CD соответственно в равных отношениях так, что AM : MB = CN : ND = m : , то выполняется равенство.

(III)

Доказательство:

Для доказательства равенства (III)
мы воспользуемся формулой (II). Запишем, что отрезки АВ и CD могут произвольно располагаться относительно друг друга (например, они могут лежать на скрещивающихся прямых и на прямых, принадлежащих одной плоскости).

Пусть О - произвольная точка, не принадлежащая ни отрезку АВ, ни отрезку CD. Соединим точку О с точками А, М, В, С, N и D и раcсмотрим векторы и .

Имеем:

,

,

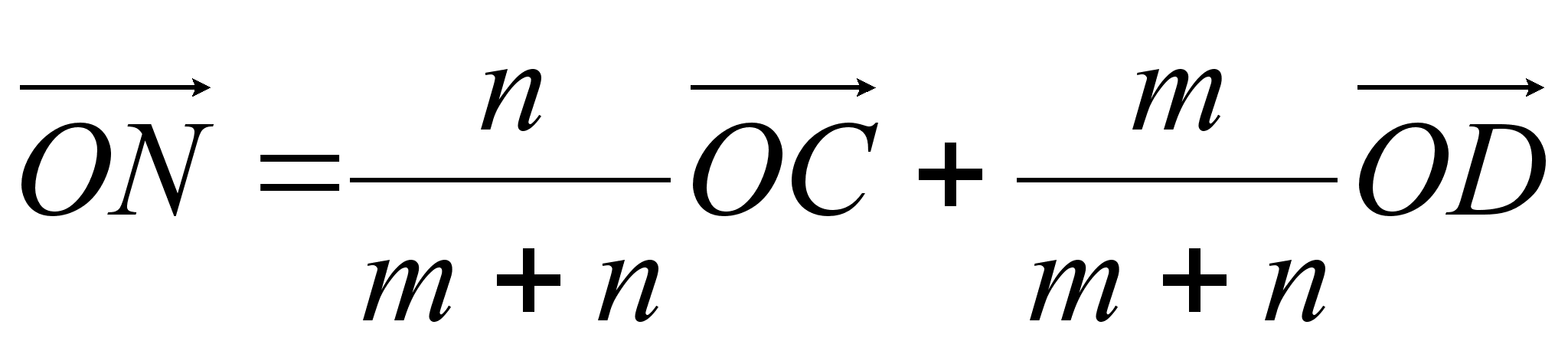Ч. т. д.

Задача. На прямой m даны три точки Р, Q, R, а на прямой m₁ -три точки P₁, Q₁, R₁ причем 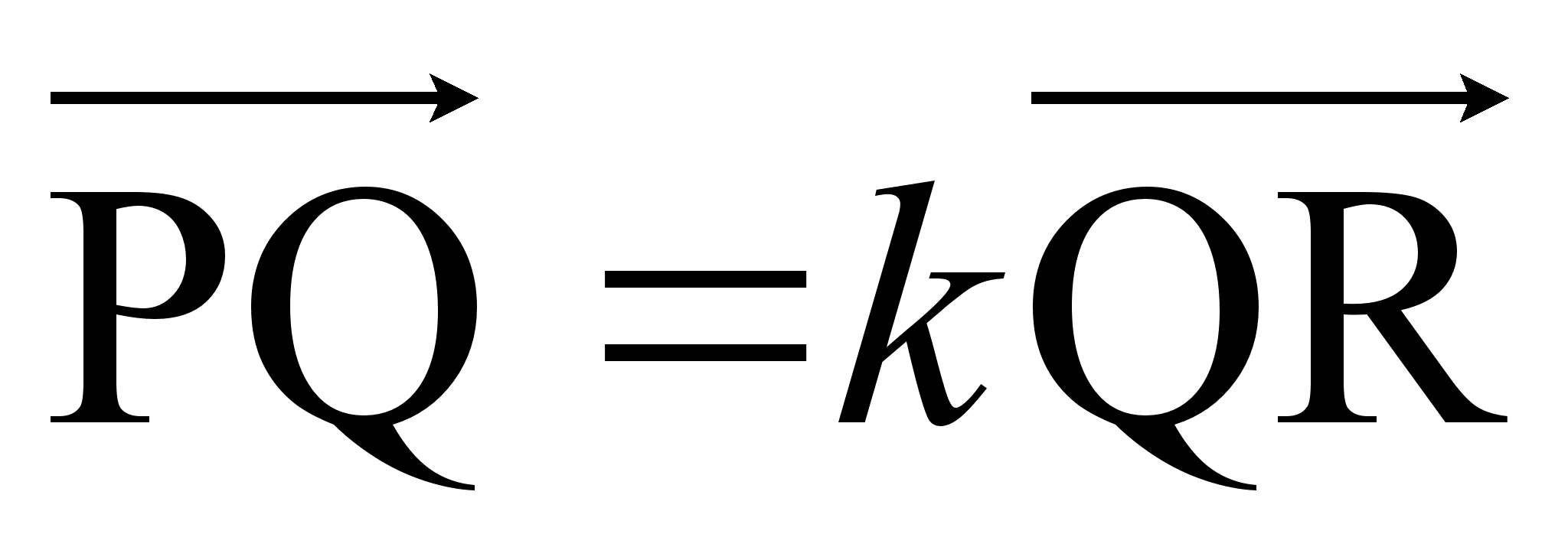, 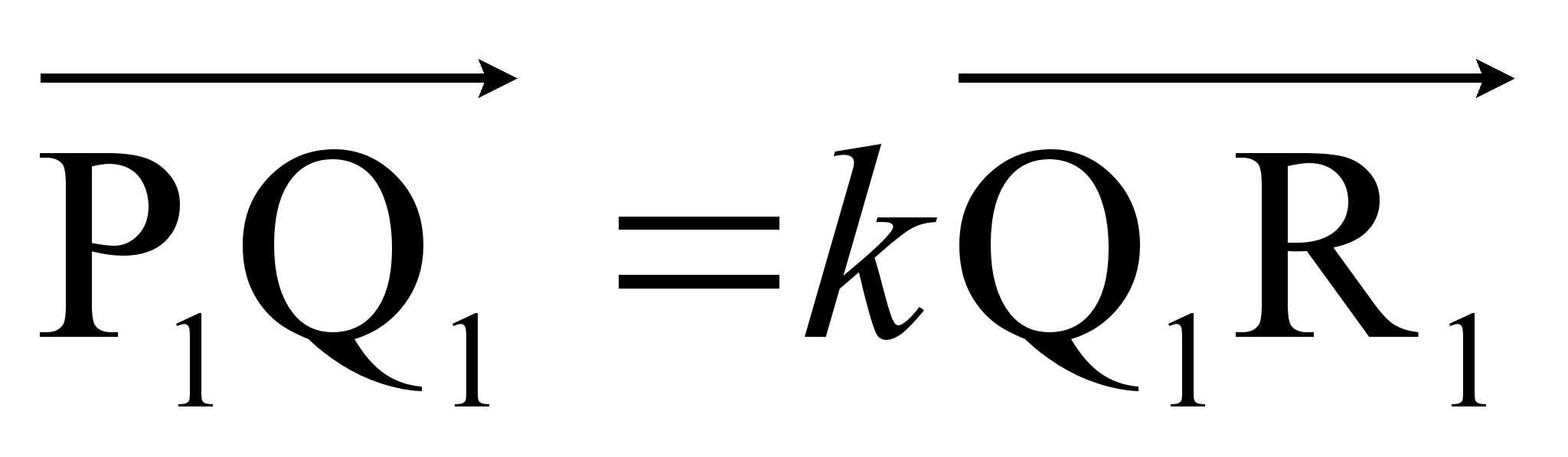. Доказать, что середины отрезков PP₁, QQ₁иRR₁ принадлежат одной прямой.

Решение.

Пусть М, N и К - середины отрезков РР₁QQ₁ и RR₁ соответственно.

На основании (III) запишем следующие векторные равенства:

(1)

(2)

Из (1) и (2) следует, что векторы и 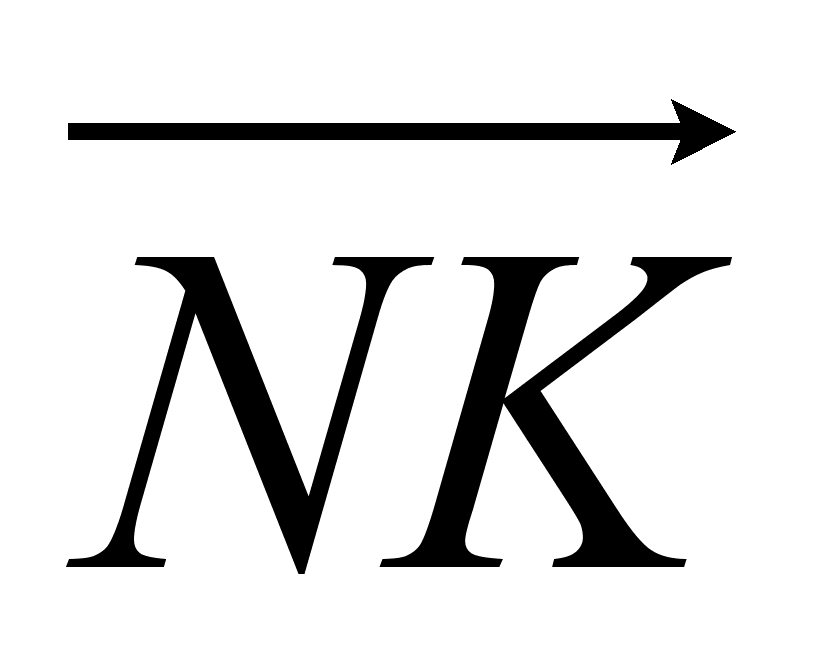коллинеарные. А так как начало одного из них является концом другого, то точки М, N и К принадлежат одной прямой.

IV Основное соотношение. Дан тетраэдр ABCD и вплоскости его грани ABCточка М. Доказать, что для разложения

Выполняется равенство

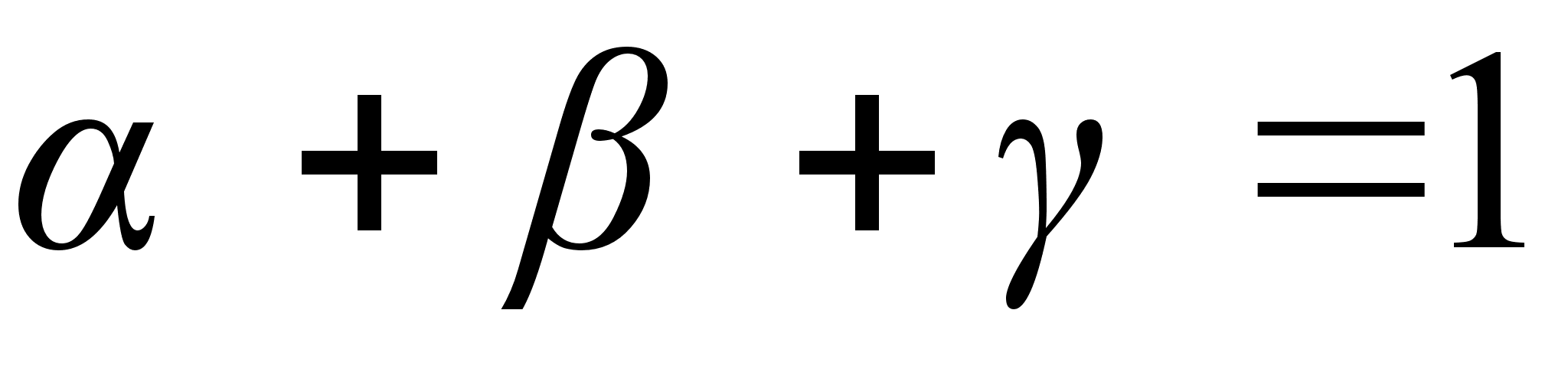
Доказательство:

Допустим, что точка М лежит внутри треугольника ABC. Проведем через точки А и М прямую, которая пересекает сторону ВС в точке Е. Пусть Е делит сторону ВС в отношении m : , т.е.

BE : EC = m : .

Тогда по формуле (II)

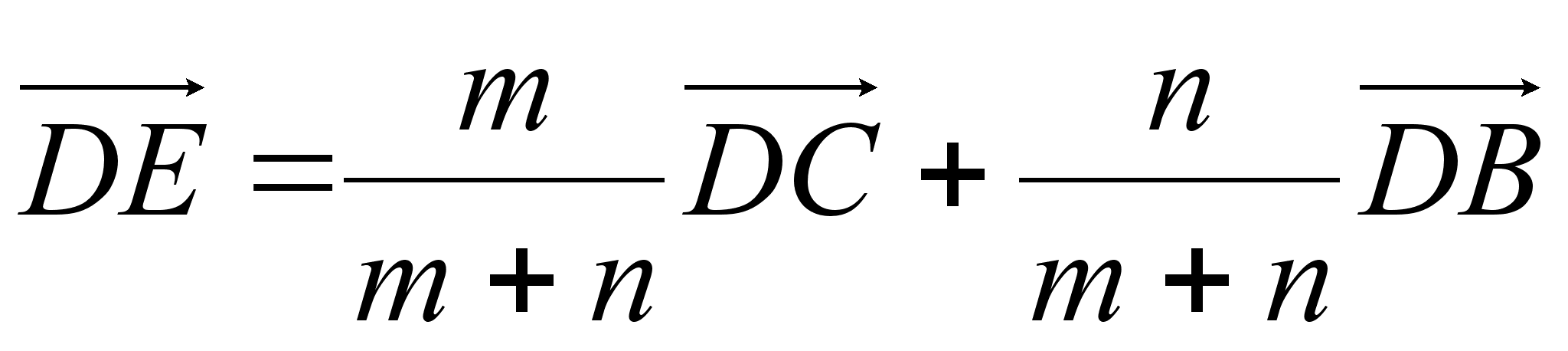
Пусть далее точка М делит отрезок АЕ в отношении : q, т.е. AM : ME = :q. Тогда

.

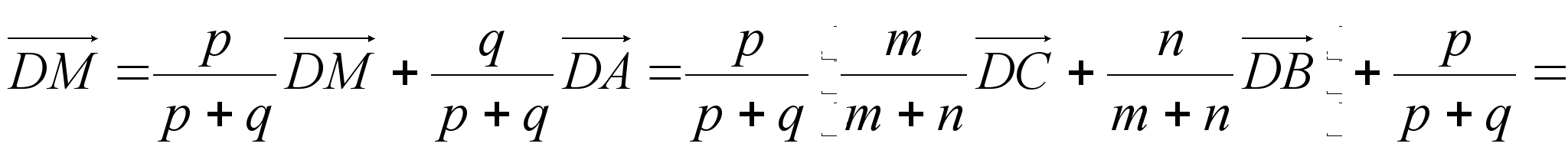
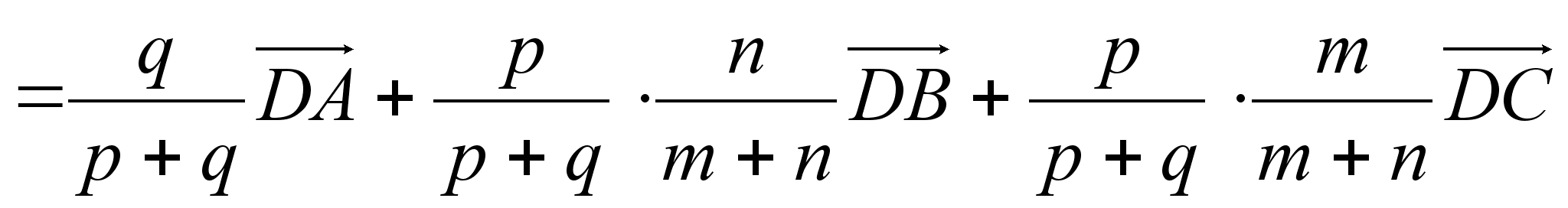Откуда

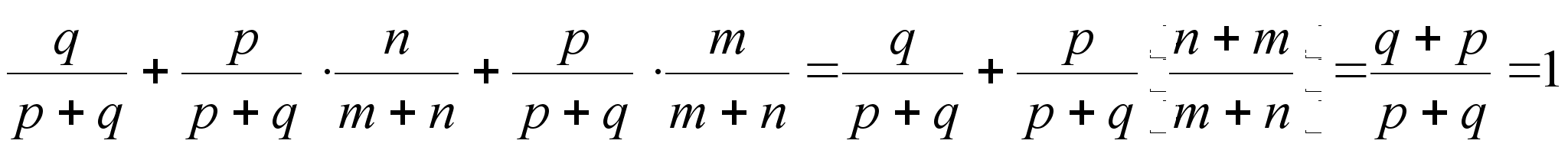
Ч. т. д.

2. Применение векторов к решению геометрических задач

В ряде случаев при решении задач на вычисление применение векторов предпочтительнее конструктивных подходов, связанных с использованием дополнительных построений, применения элементарной алгебры и тригонометрии.

Чтобы успешно решать геометрические задачи посредством векторов, требуется не только знание законов векторной алгебры, знакомство с понятием разложения вектора в базисе , умение переводить геометрический факт на язык векторов, но и определенная методика при составлении плана решения. Отметим несколько важных положений.

1. Если требуется вычислить расстояние или угол, то надо применять скалярное умножение векторов.

2. При введение векторов можно идти двумя путями:

а) выбрать точку от которой откладывается известные векторы;

б) векторы изображать направленными отрезками, связанными с рассматриваемыми в задаче фигурами, не откладывая их от одной точки.

3. Если задача планиметрическая, то целесообразно выделить два неколлинеарных вектора в качестве базисных и остальные векторы выразить через них; если же задача стереометрическая, то в качестве базиса следует выбрать три некомпланарных вектора. При этом введение начальной точки необязательно.

4. В ряде случаев, например при решении задач на многогранные углы,

вычисления упрощаются, если ввести единичные векторы, отложенные от вершины многогранного угла.

Примеры задач, решаемых векторным методом.

Задача. Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равнобедренного прямоугольного треугольника.

Решение.

Пусть и ;

Согласно условию .

Вектор 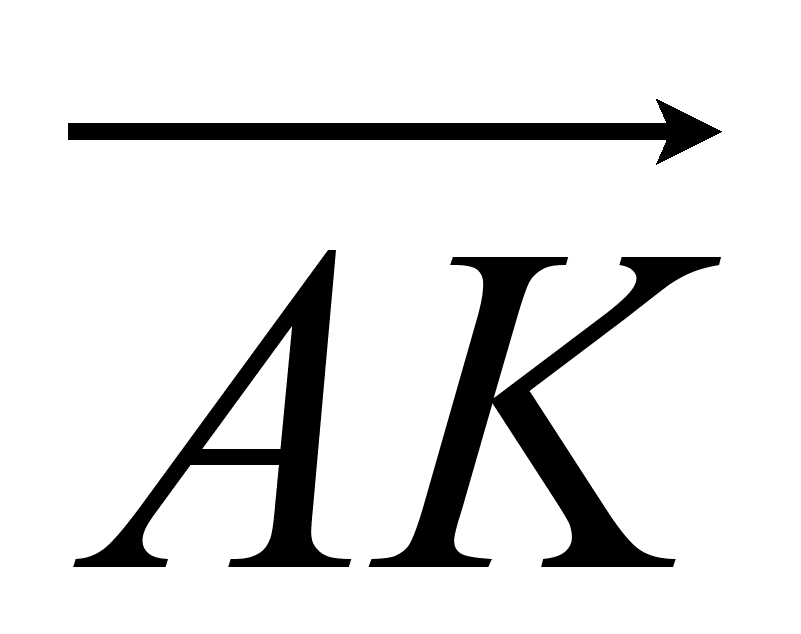есть разность векторов и , т.е. (т.к. ).

Аналогично .

Угол междувекторами находится по формуле:

,

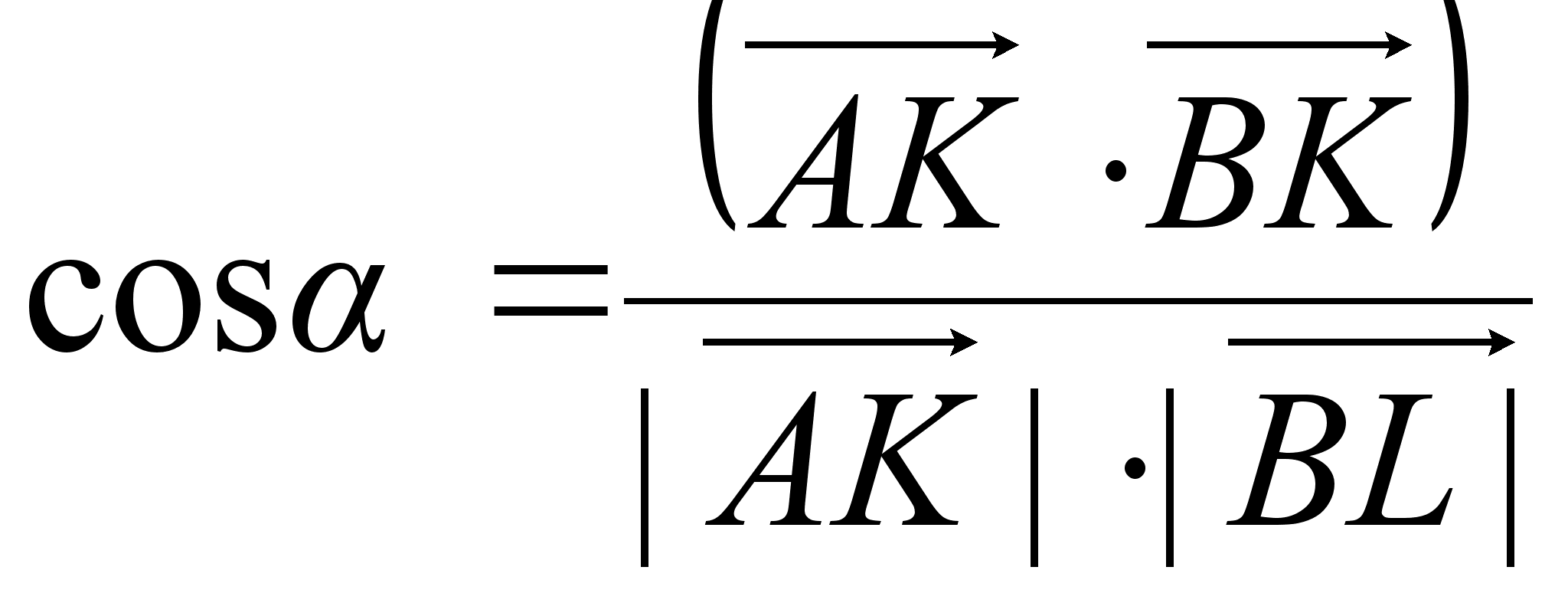
но, , т.к. . Следовательно

.

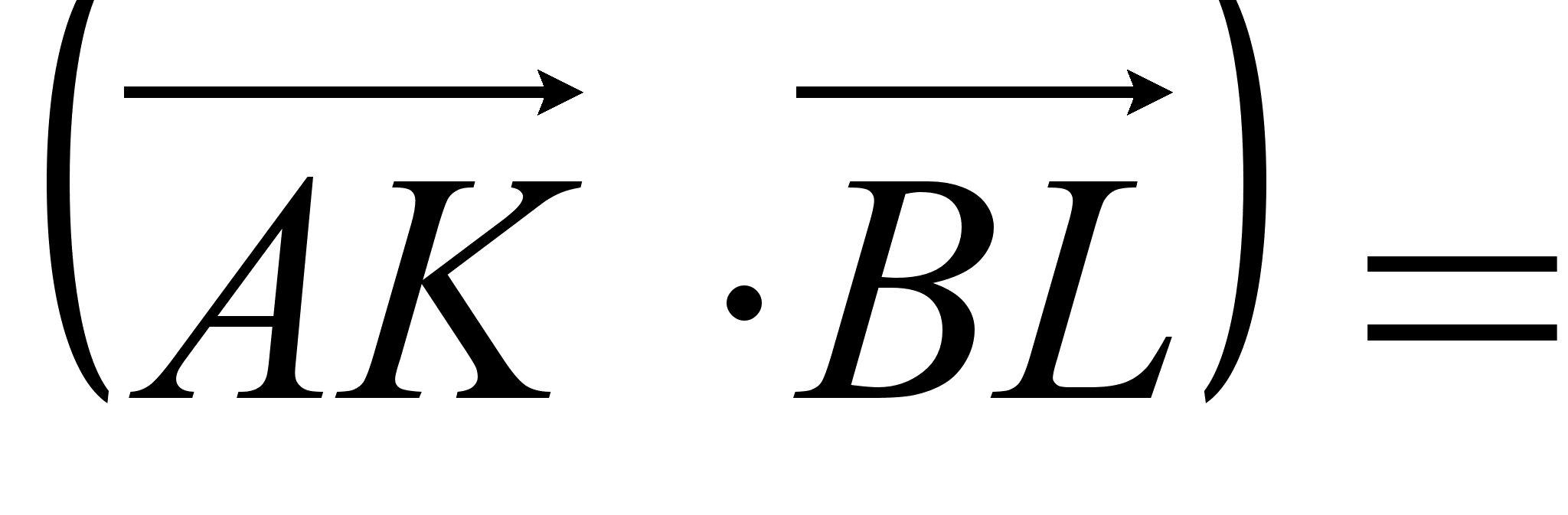
длины векторов 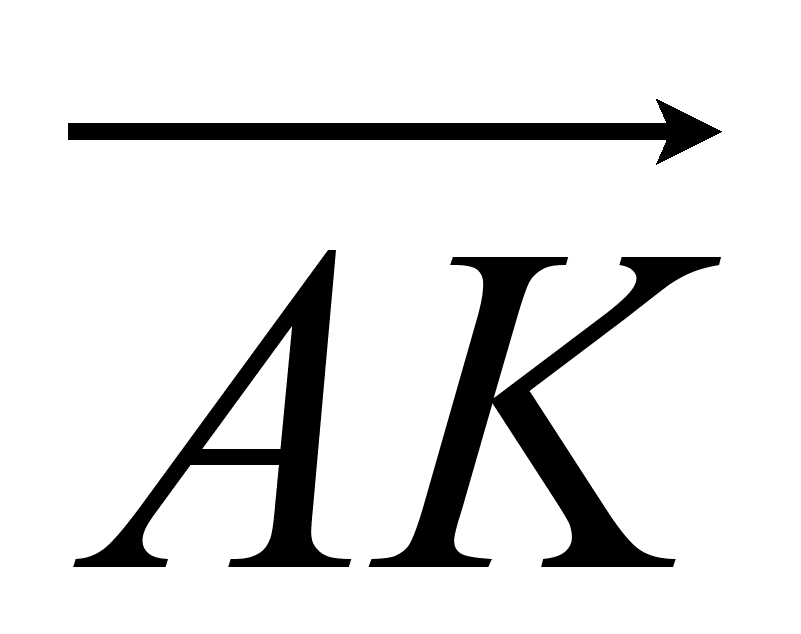и найдем по теореме Пифагора.

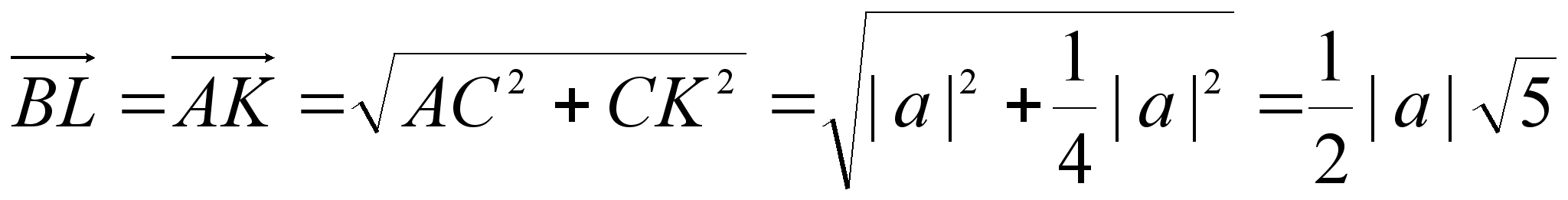
Таким образом

Тогда

Ответ:

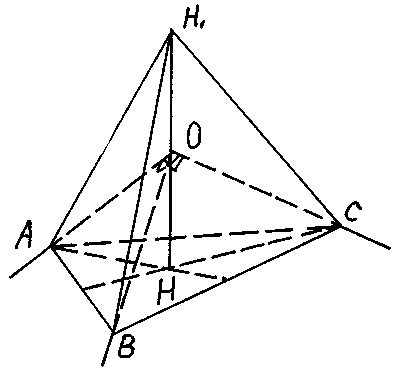
Задача. На ребрах прямоугольного трехгранного угла с вершиной О отложены равные отрезки ОА, ОВ, ОС. Из точки О на плоскости ABC опущен перпендикуляр ОН. Доказать, что если точка Н₁ симметрична точке Н относительно вершины О, то тетраэдр Н₁ABC правильный.

Решение:

Примем вершину О трехгранного угла за начало векторов. Тогда

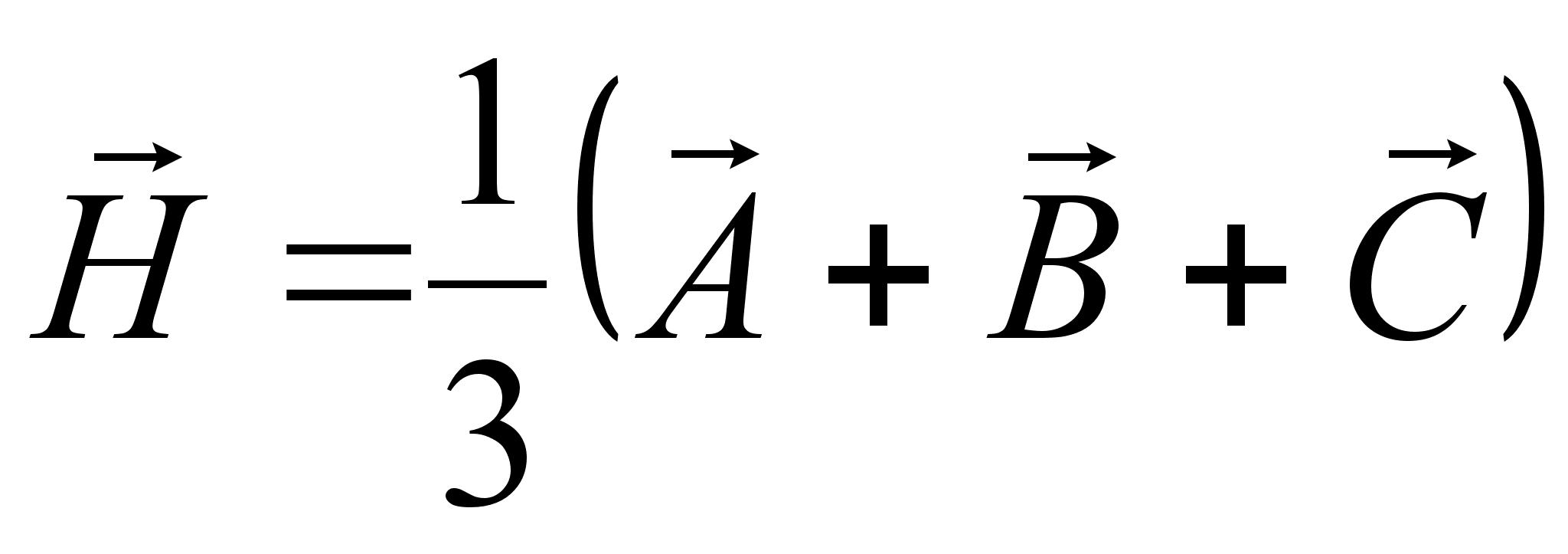
и .

Следовательно,

,

.

Найдем

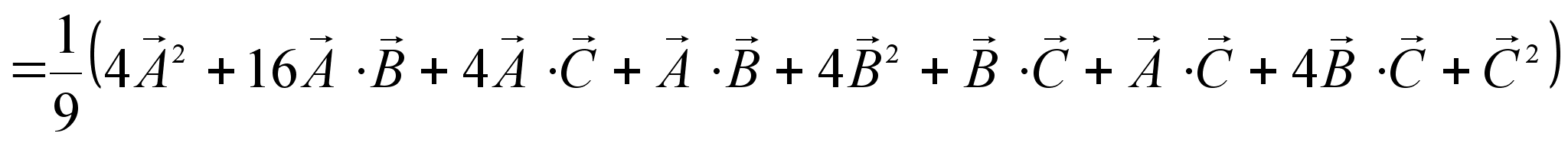
Учитывая, что и , имеем: .

Далее находим:

,

,

.

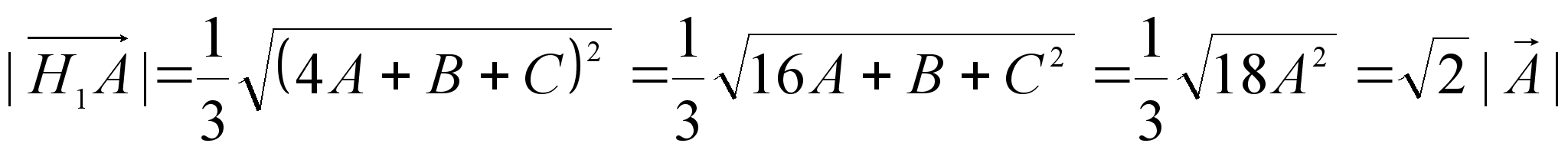Это значит , что отрезки H₁A и H₁B равны и образуют угол 60°, т.е. треугольник H₁AB правильный.

Аналогично устанавливается, что две другие грани H₁BC и H₁CA являются равносторонними треугольниками и вследствие этого тетраэдр правильный.

Задача. Доказать, что можно построить треугольник, стороны которого равны и параллельна медианам данного треугольника ABC.

Решение.

О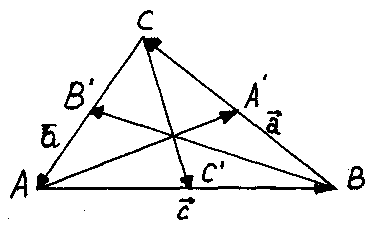бозначим середины сторон ВС, СА и АВ соответственно А’, B’, C’. Выразим векторы, представляющие медианы треугольника ABC, через , , (через стороны данного треугольника):

,

,

.

Составим сумму сторон треугольника ABC

.

Но так как векторы 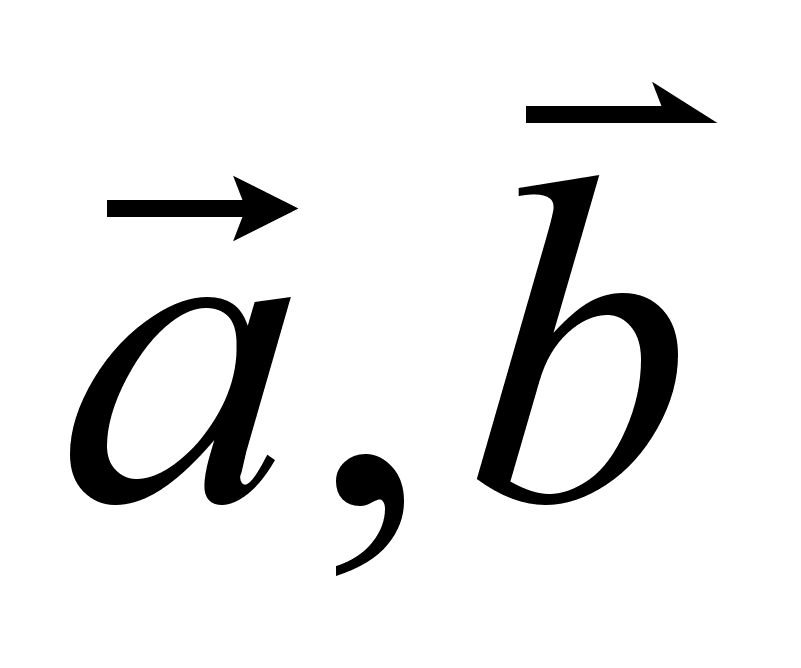и образуют данный треугольник ABC, то их сумма равна нулю, следовательно, и . А это значит, что из векторов 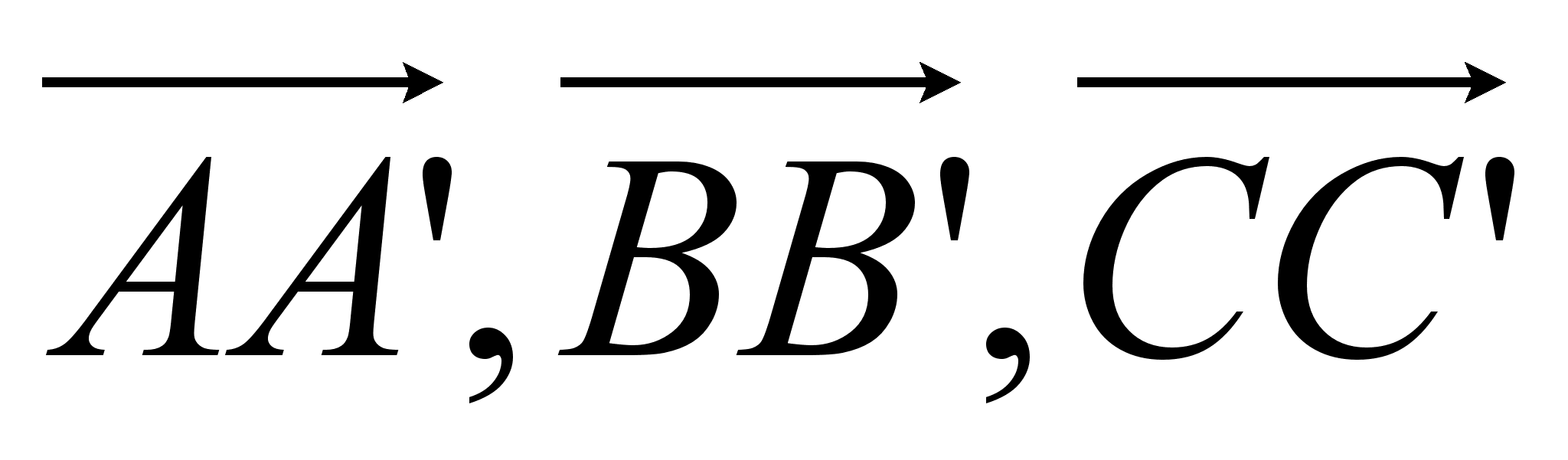можно построить треугольник.

Задача. В треугольнике ABCDточка Е и F – середина рёбер АВ и CD соответственно. Доказать, что середины отрезков СЕ, DE, AFи BFявляются вершинами параллелограмма.

Решение. Пусть К, L, М, N - середины отрезков СЕ, DE, AF и BF, соответственно. Доказать, что середины отрезков СЕ, DE, AF и BF являются вершинами параллелограмма.

Докажем равенство векторов 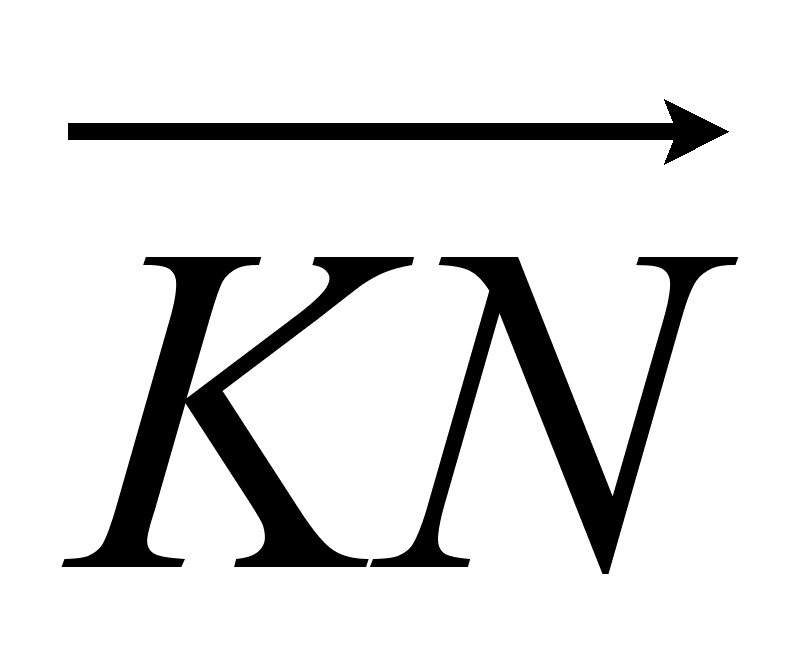и , выразив их через векторы , , , , где О – произвольная точка.

(1)

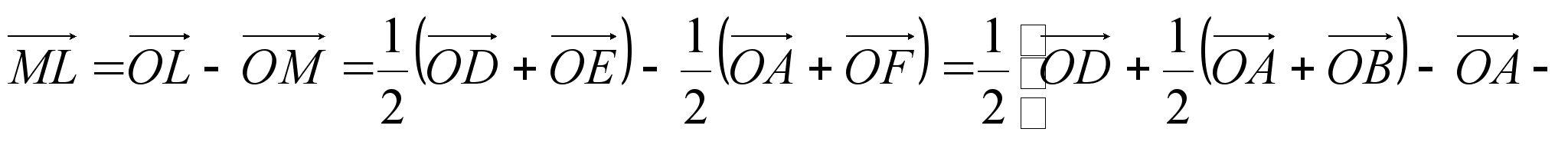
. (2)

Ч. Т. Д.

Задача. Точки К, L, M на сторонах АС, ВС, АВ треугольника ABC таковы, что 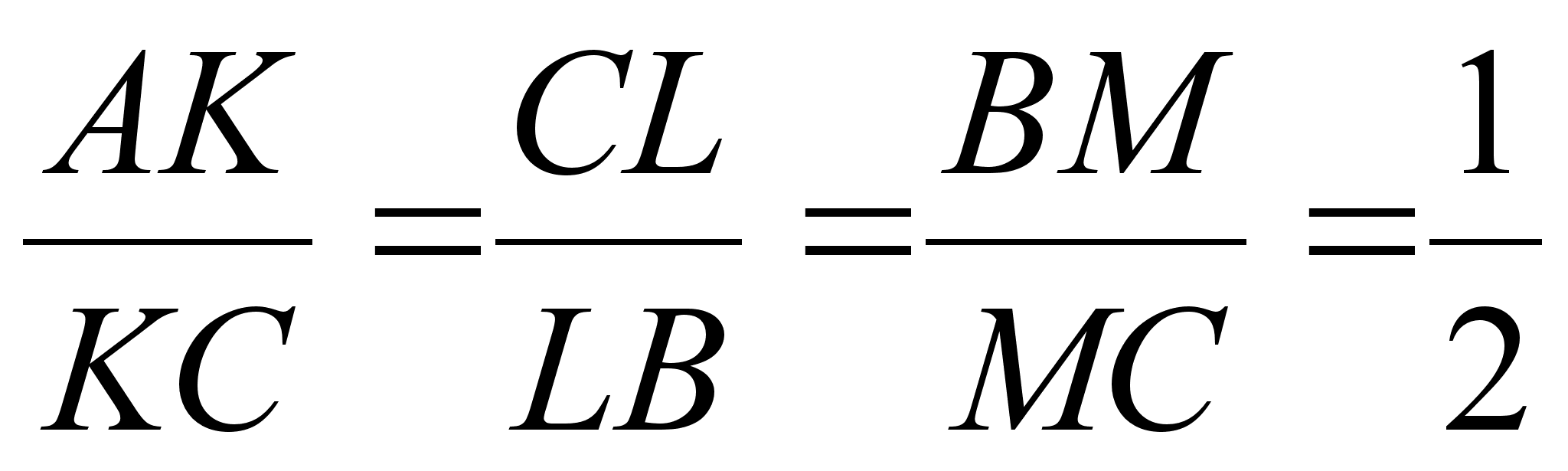, N – середина сторона АС. Найти отношение в котором точка пересечения отрезков KL и MN делит отрезок KL.

Решение.

Обозначим через О точку пересечения отрезков MN и KL и через х отношение KO : KL. Тогда . Учитывая, что L – середина МС и 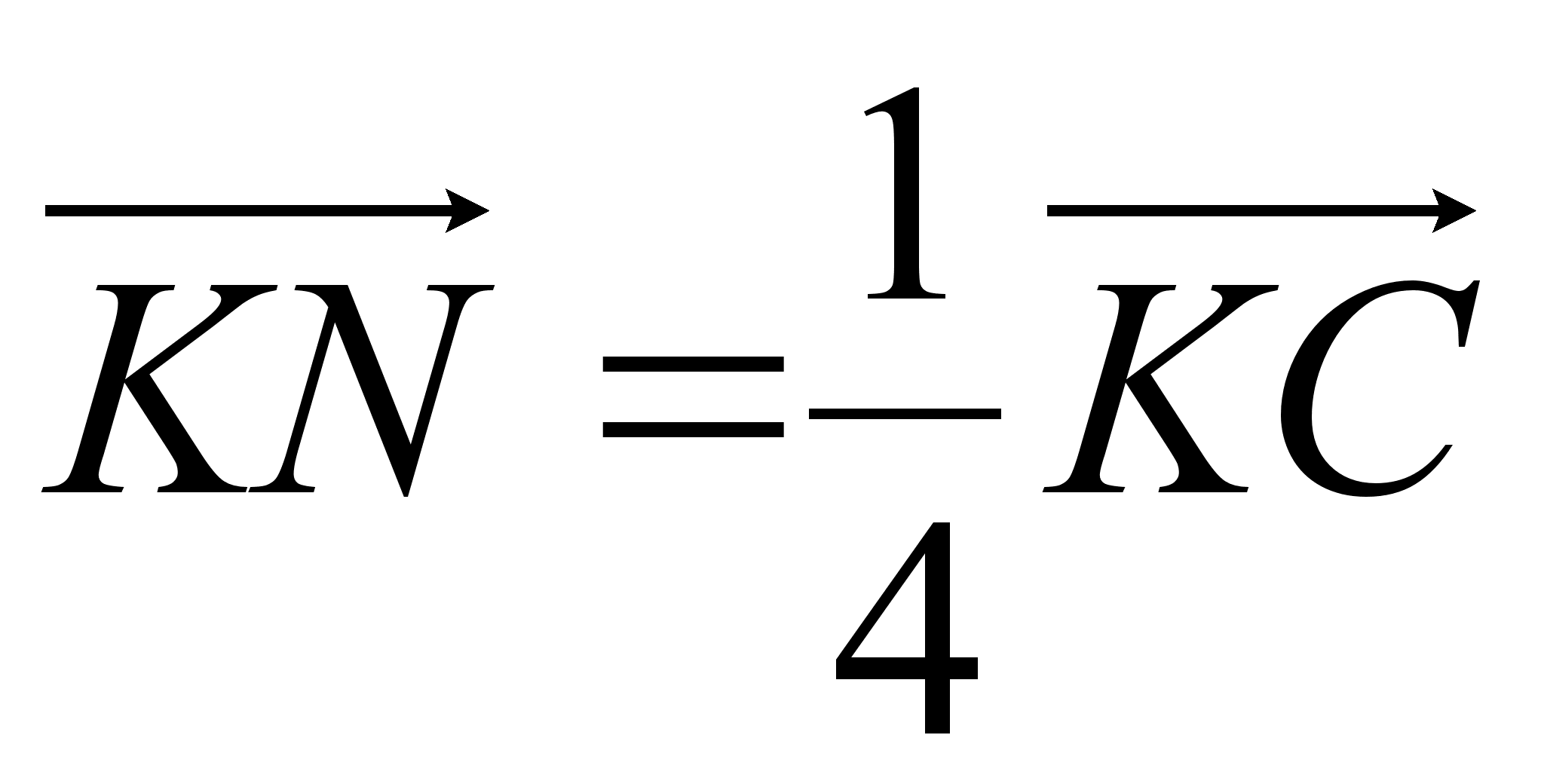,получаем

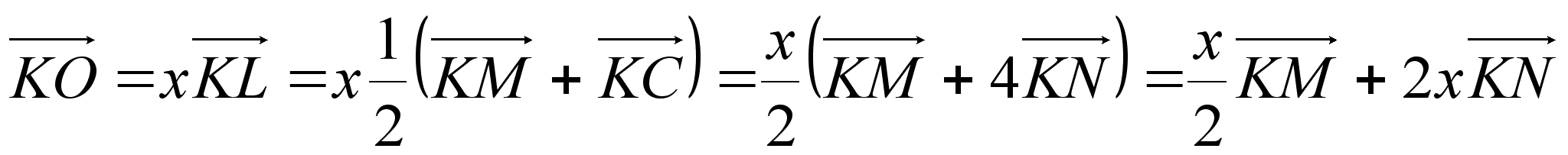
Так как точка О лежит на прямой MN, то . Откуда . Значит, .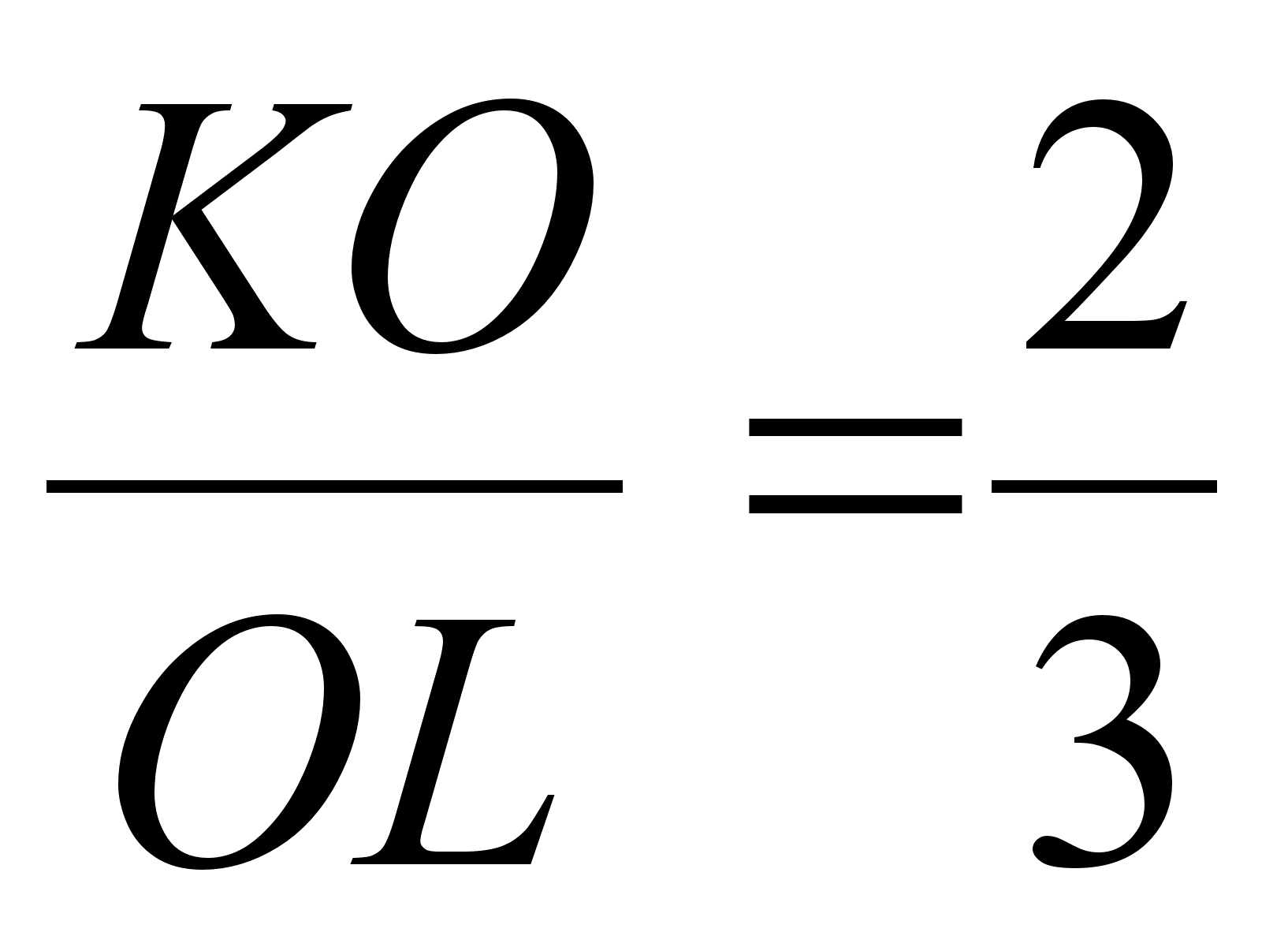

Ответ: KO : OL = 2:3

Задача. Отрезки DA₁, DB₁, DC₁ – медианы граней BCD, ACD и ABD тетраэдра ABCD соответственно. Точки К, М, N делят отрезкиDA₁, DB₁, DC₁ в отношении 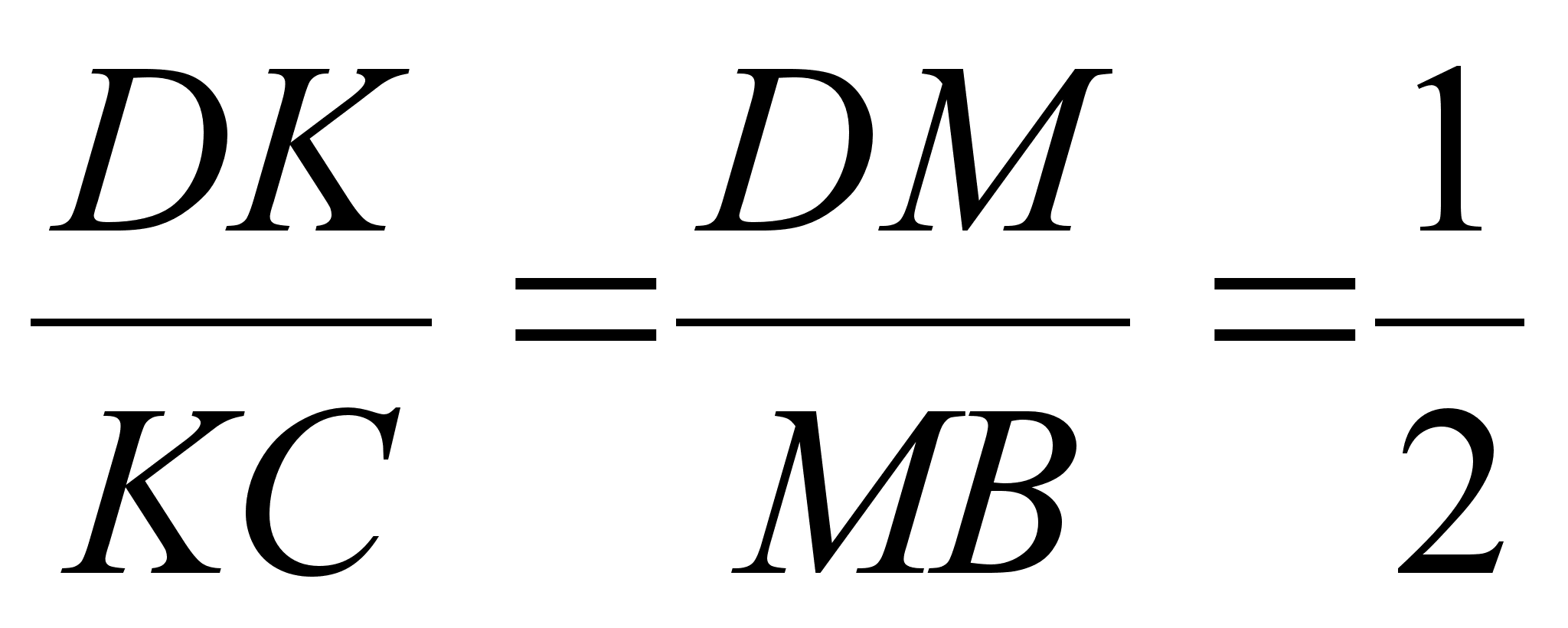, 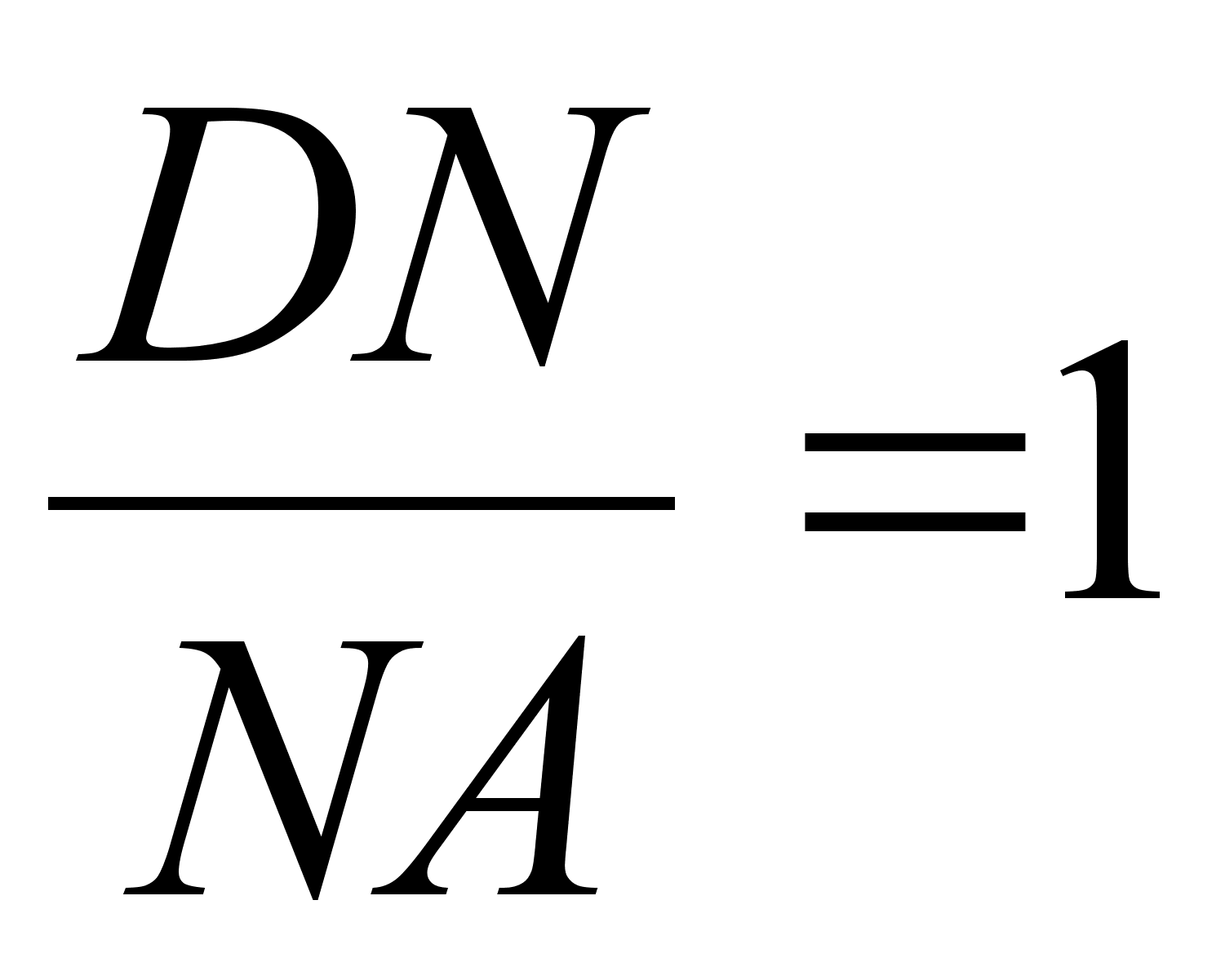. В каком отношении плоскость KMN делит ребра DA и DB ?

Решение.

Пусть плоскость KMN пересекает ребра DA, DB и DC тетраэдра ABCD в точках Р, Q, R соответственно.

Точки А₁, В₁, С₁ – середины отрезков ВС, АС, АВ соответственно. Следовательно,

Решив эту систему, (например, сложив (1) и (2), и вычтя (3) получим

Пусть . Тогда, учитывая , , ,

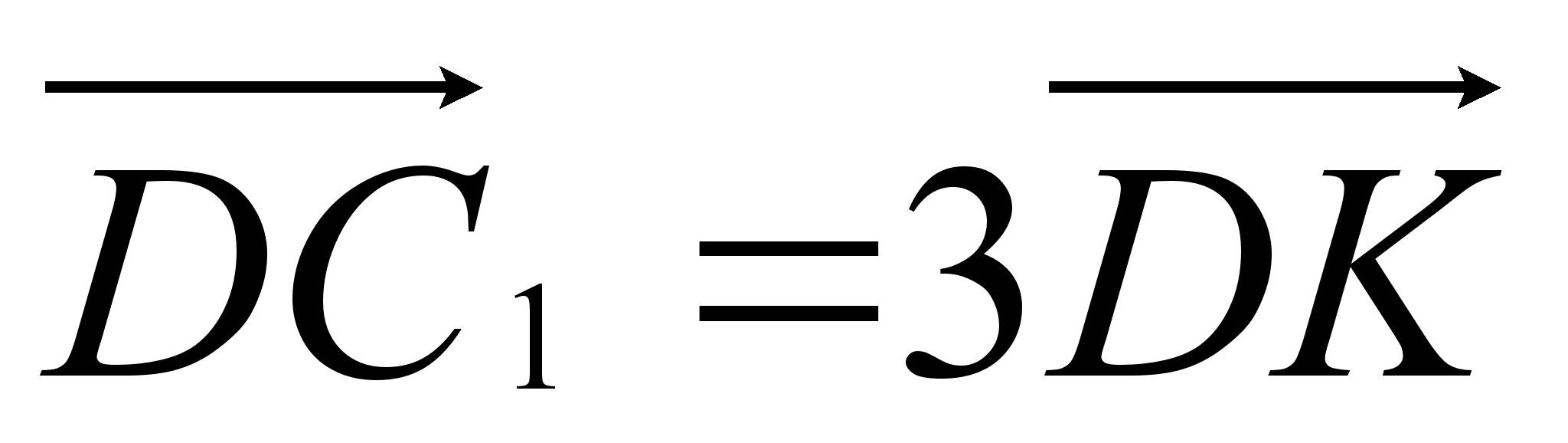имеем

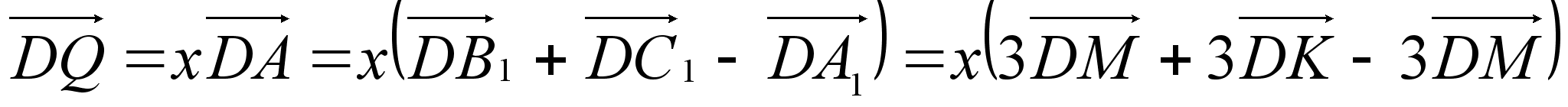, и, т.к. точки К, М, N, Р лежат в одной плоскости, то

.

Таким образом, , откуда .

Пусть теперь 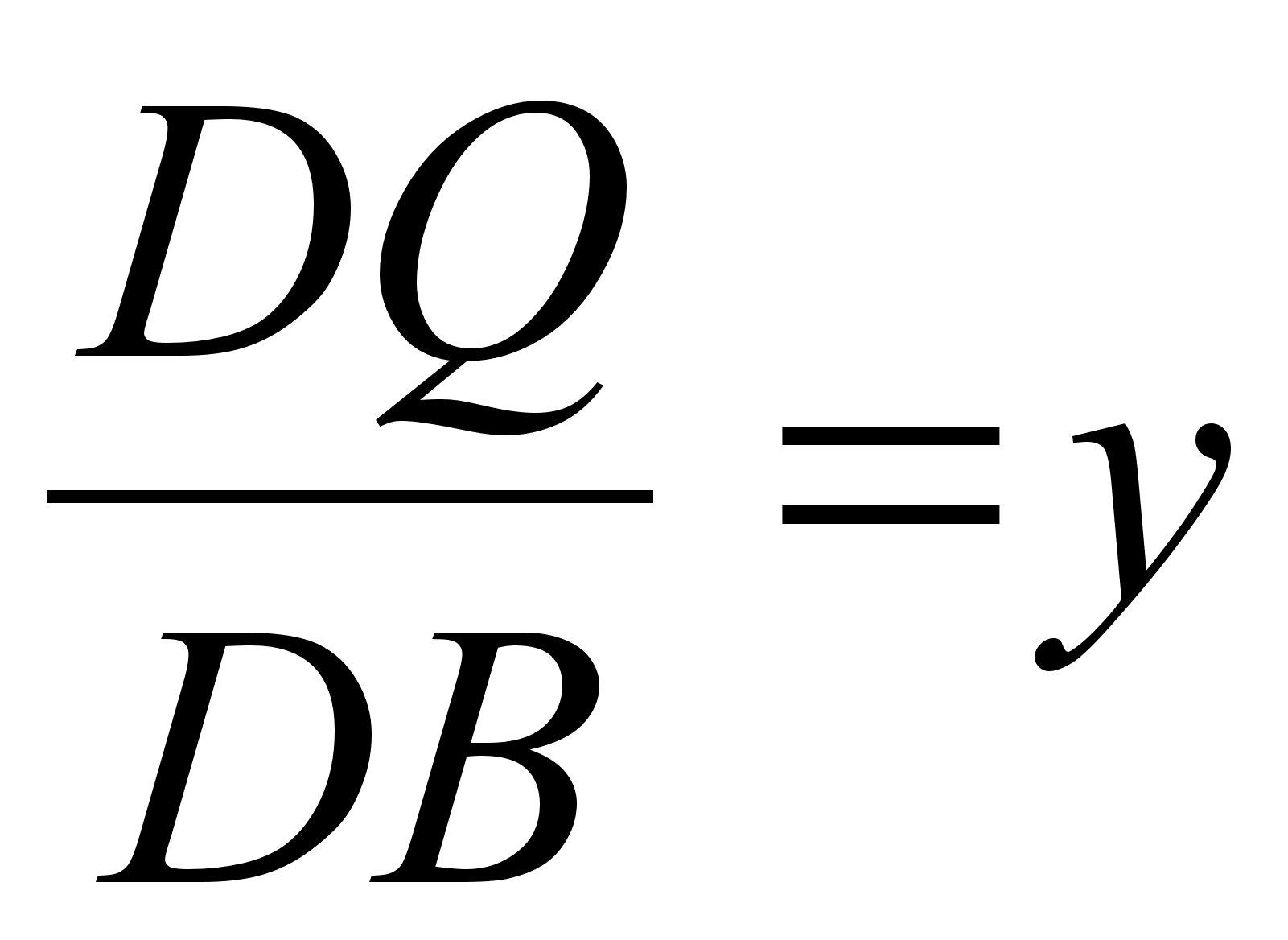, тогда

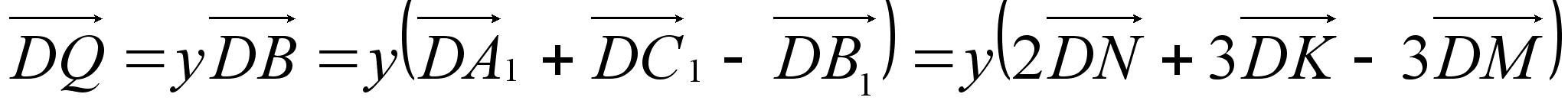, и

, откуда

Ответ: , .

Задача. Основанием пирамиды SABC является равносторонний треугольник ABC, длина стороны которого равна 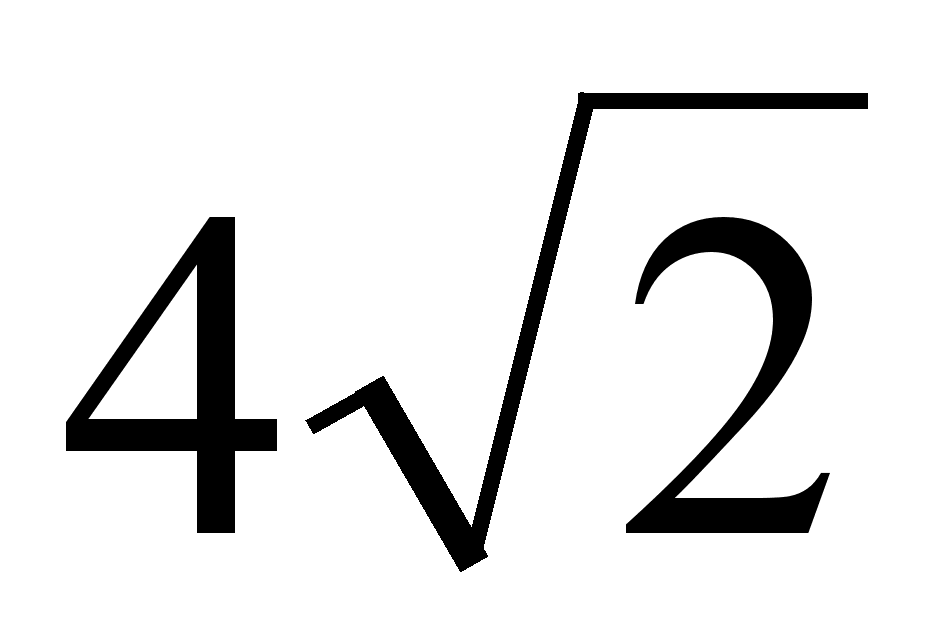. Боковое ребро SC перпендикулярно плоскости оснований и имеет длину 2. Найти угол между прямыми, одна из которых проходит через точку S и середину ребра ВС, а друга проходит через точку С и середину ребра АВ.

Решение. Обозначим .

Выберем в качестве базиса векторы , и .

Тогда, из треугольника BCS: ,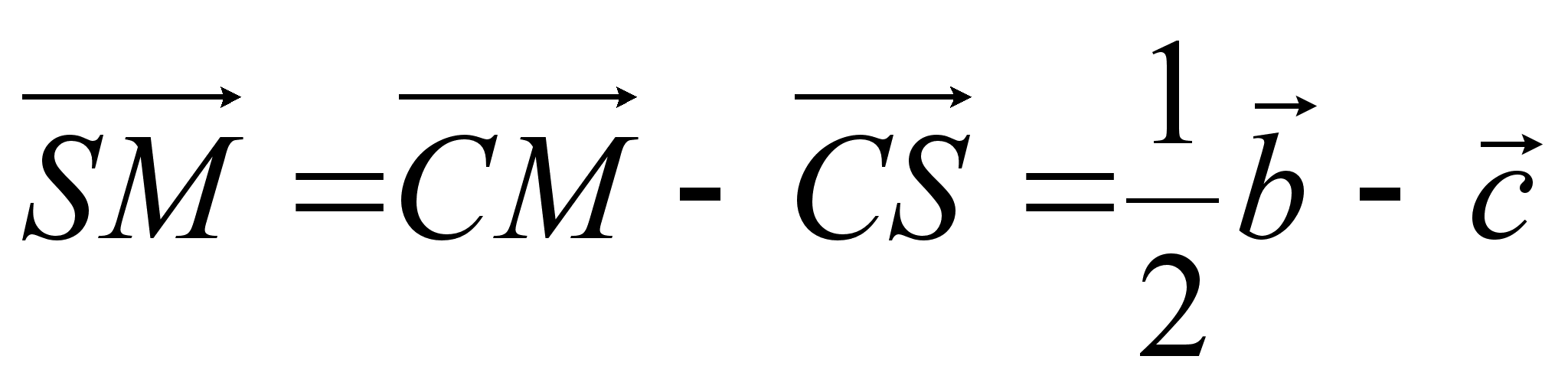

а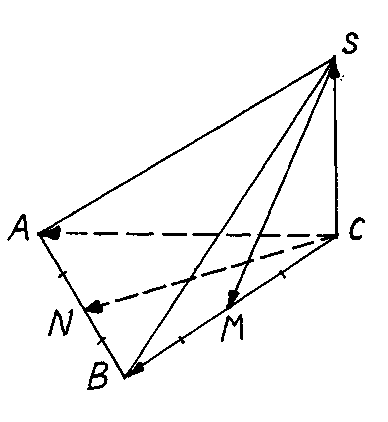 из треугольника ABC: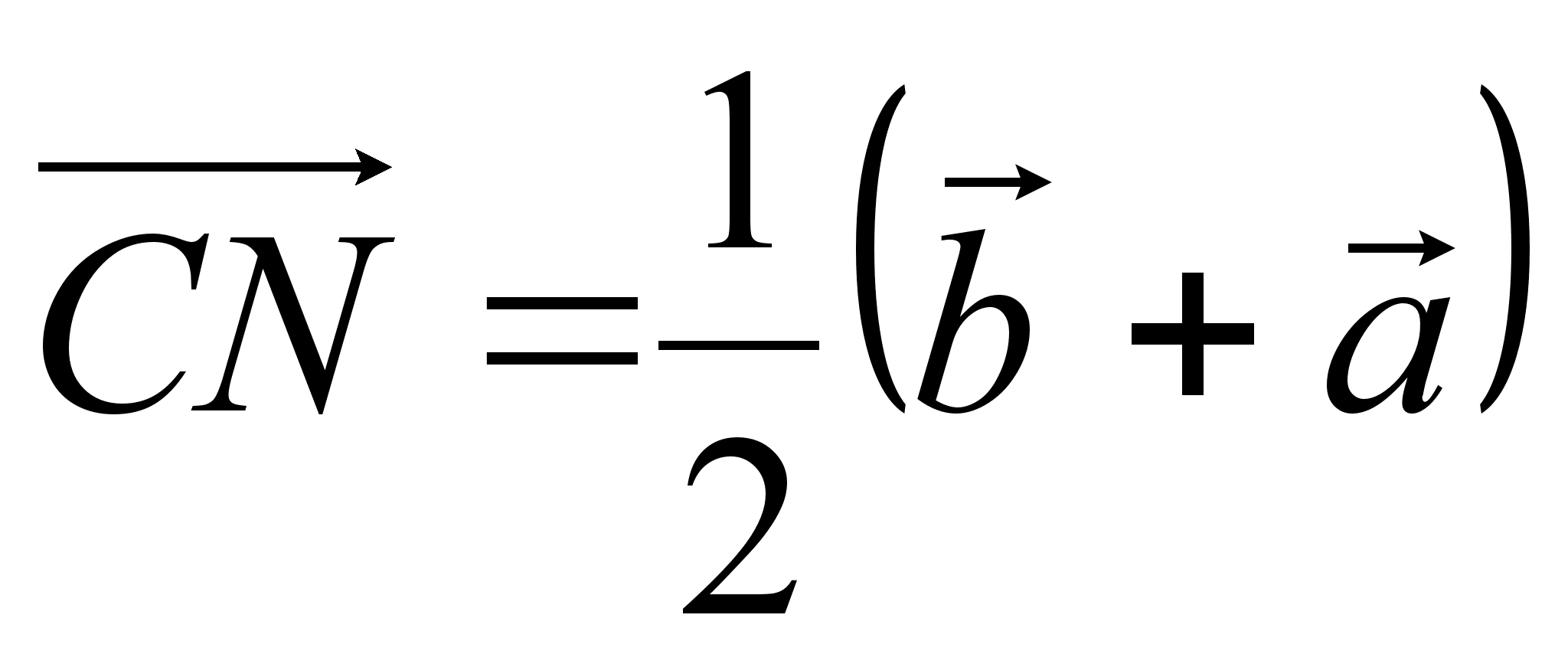

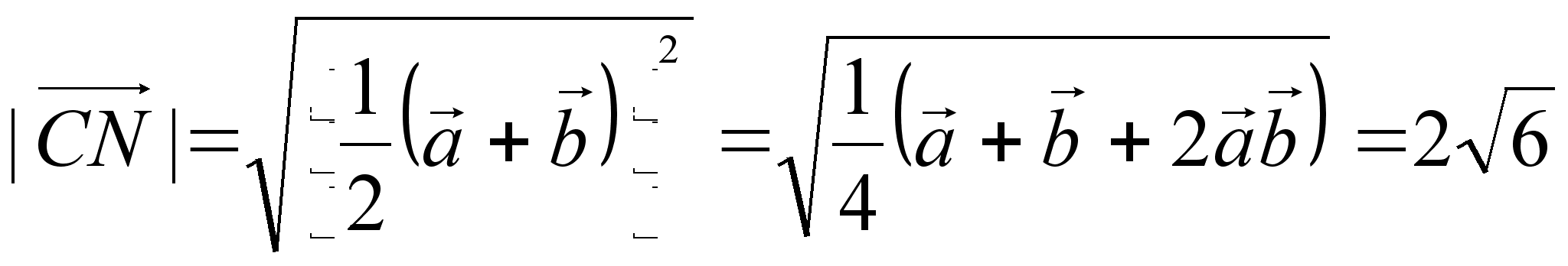
Ответ: .

Задача. Каждое ребро призмы ABCA₁B₁С₁ равно 2.

Точки М и N – середины ребер АВ и A₁А. Найти расстояние от точки М до прямой CN, если известно, что угол A₁AС paвeн 60° и прямые A₁A и АВ перпендикулярны.

Решение.

Рассмотрим базис, состоящий из векторов , , и составим таблицу умножения для этих векторов.

*	а		с
а	4	0	2
	0	4	2
с	2	2	4

Расстояние от точки М до прямой CN равно расстоянию от точки М до её проекции на прямую CN.

Пусть Р – проекция точки М на прямую CN.

Тогда

для некоторого числа х.

Так как 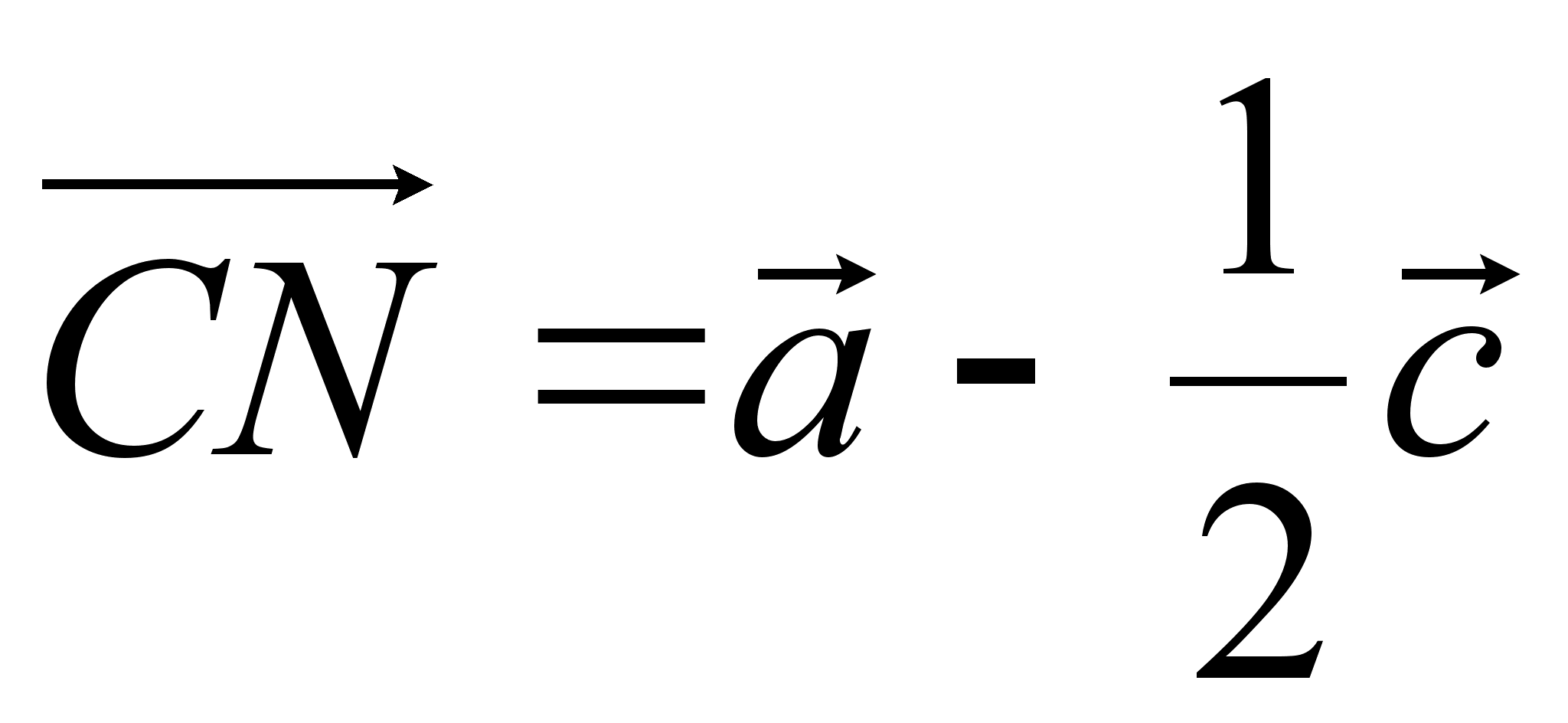и ,

Поскольку прямые и перпендикулярны, то т.е.

.

Раскрывая скобки и пользуясь таблицей умножения для нашего базиса, получаем: .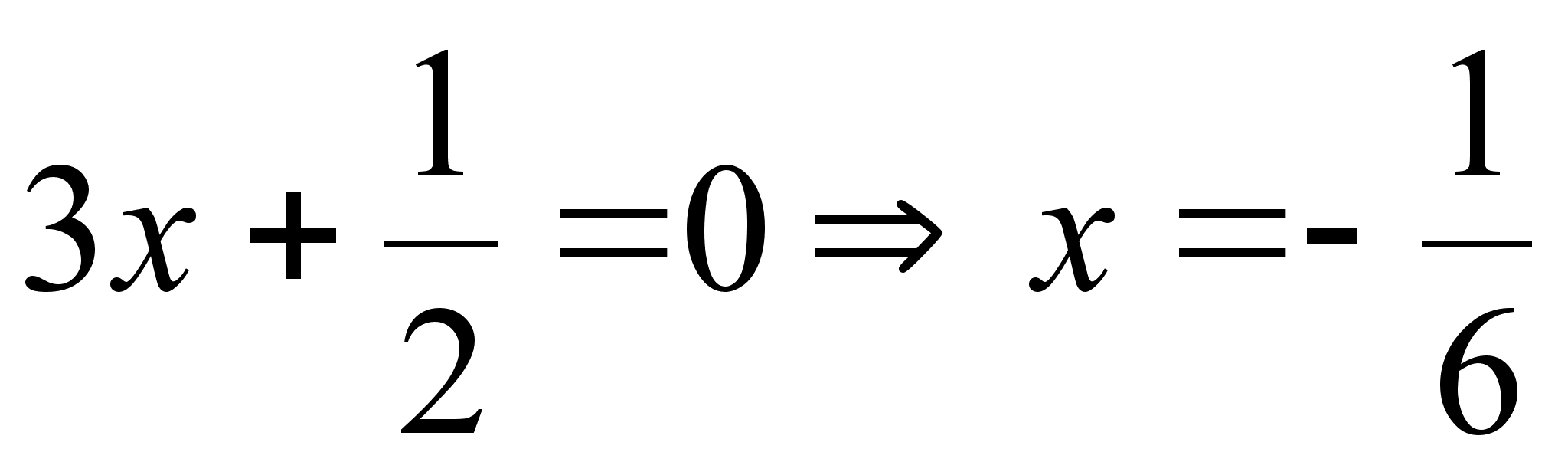

Тогда .

Искомое расстояние равно

Снова раскрывая скобки и пользуясь таблицей умножения, находим . Таким образом, расстояние от точки М до прямой равно .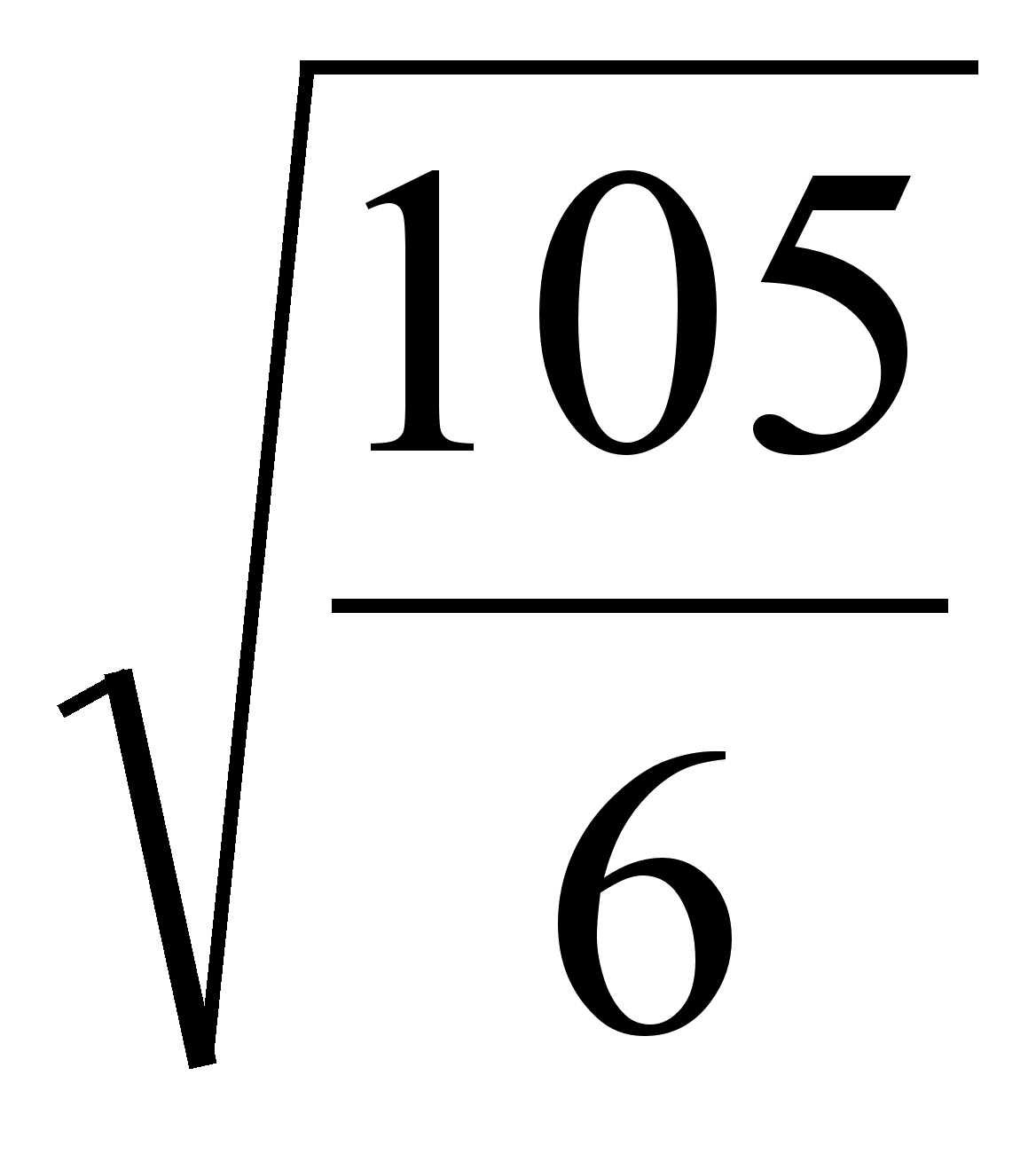

Ответ : расстояние равно .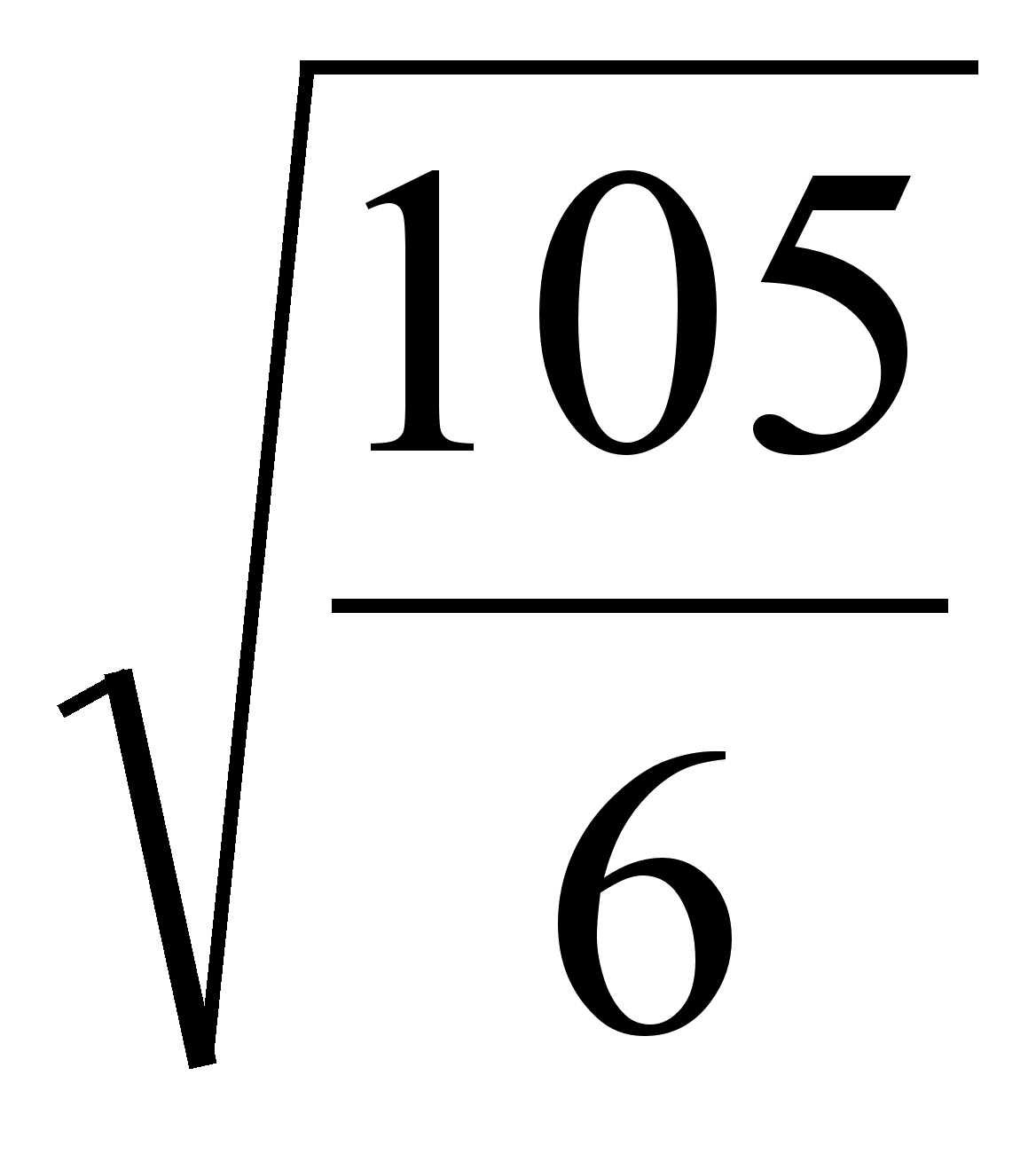

у ⁶

Задача. В параллелограмма ABCD точка К – середина стороны ВС, а точка М – середина стороны CD. Найдите AD, если АК = 6, АМ = 3, угол КАМ= 60°.

Решение.

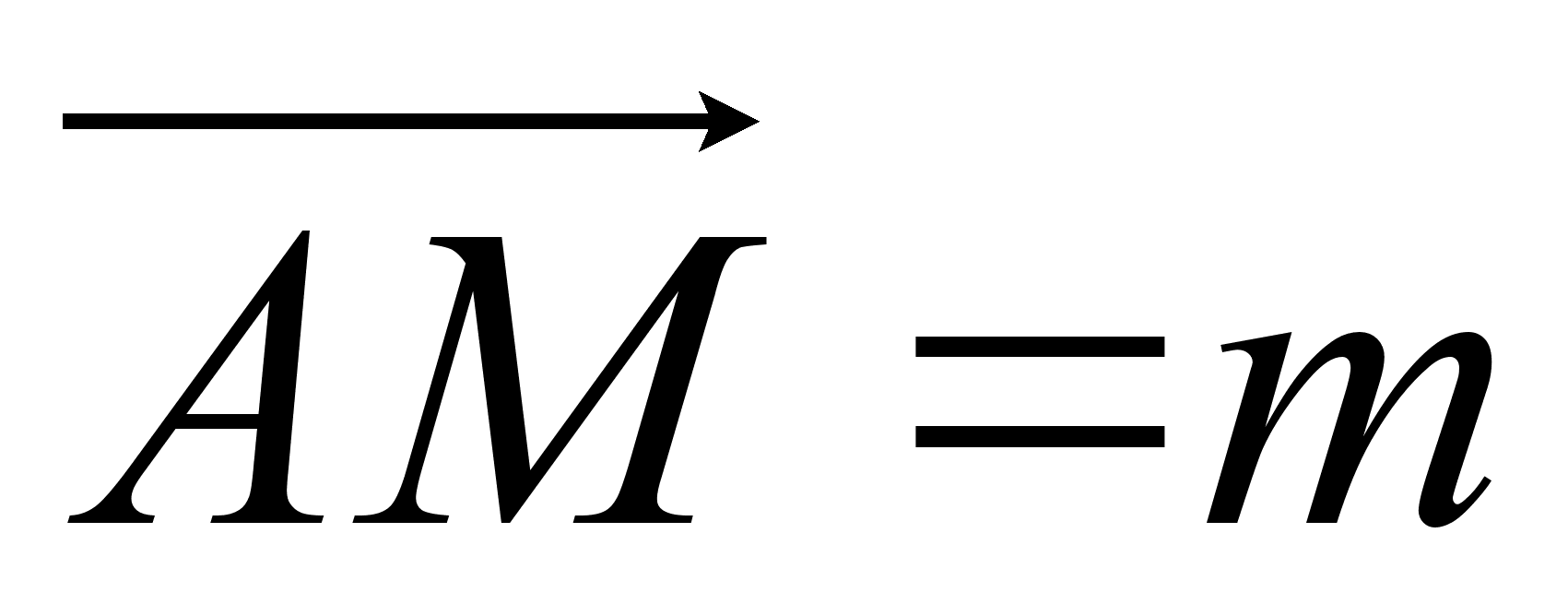В качестве базиса выберем векторы и 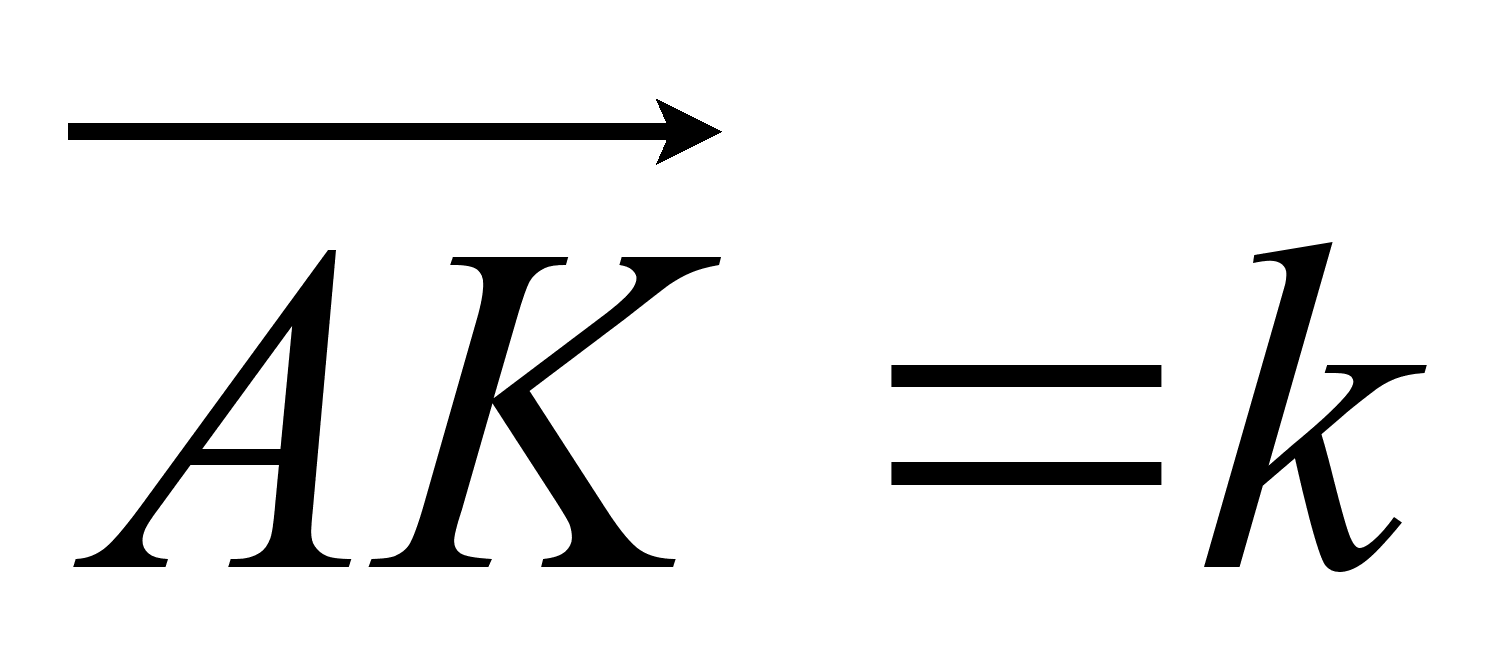и составим таблицу умножения для векторов этого базиса.