Шпаргалки на экзамен в ВУЗе (1 семестр, математика)
1) Основные понятия линейной алгебры. Задачи о перевозках. Элементы линейной алгебры. Задачи о перевозках. На 2-х складах А1 и А2 сосредоточено а1, а2 тон однородного груза, которые нужно доставить в 3-и пункта назад в В1, В2, В3, потребн пунктов назначения, равны в1, в2, в3 тон. Известно стоимость перевозки одной тонны груза, из каждого пункта отправления в каждый пункт назначения. Требуется составить такой план перевозки, при котором общая стоимость перевозок была бы наименьшей. А1+А2=В1+В2+В3 Хij – груз(тон) Сij – цена 1т груза. С= Т.о задача ставится к нахожд неизвестного X и ij удовлетвор системе Ур-ий Причем найден Ур-е должны быть такими чтобы ф-я приняла миним з-я. Для реш сформир задачи необходимо уметь решать системы лин Ур-й , т.к. система явл сист лин Ур-й относит xij. Сист m лин Ур-й с n нейзв x1, x2,…,Xn имеет вид а11x1+а12x2+…+a1nXn=b1; a21x1+a22x2+…+a2nXn=b2;…….;am1x1+am2x2+…amnxn=bm.Коэфициенты аij при неизвестн xij (j =1,2,…n), для удобства обозн одной буквой с 2-я индексами i-номер Ур-нии, j- неизвстного |
10)Метод Гаусса.(Карл Фридрих Гаусс (1777-1855) немецкий математик)В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.Рассмотрим систему линейных уравнений: |
11) Векторы, действия над ними.Определение.Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.Определение.Длиной (модулем) вектора называется расстояние между началом и концом вектора. |
12)Скалярное произведение векторов, его св-ва и вычисления. Определение. Скалярным произведением векторов |
13)Векторное произведение векторов. Его св-ва и вычисление. Определение.Векторным произведением векторов 3
Свойства векторного произведения векторов:1) |
14)Смешенное произведение векторов его св-ва и вычисления.Определение.Смешанным произведением векторов
Свойствасмешанного произведения: 1)Смешанное произведение равно нулю, если: а)хоть один из векторов равен нулю;б)два из векторов коллинеарны;в)векторы компланарны. 2) 4) Для нахождения длины высоты пирамиды найдем сначала площадь основания CD. Sосн = |
15) Общее вычисление прямой на плоскостиОпределение. Любая прямая на плоскости может быть задана уравнением первого порядкаАх + Ву + С = 0,причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой.В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. |
Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением: |
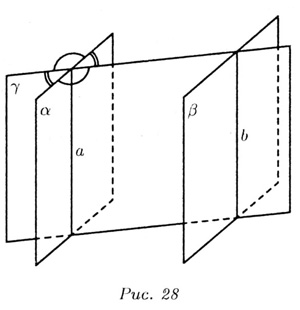
17)Взаимное расположение двух плоскостей характеризуется двумя возможностями.1). Две плоскости не имеют общих точек, и , в таком случае, они называются параллельными (на рис. 28
Две плоскости имеют хотя бы одну общую точку, и в таком случае они называются пересекающимися. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат обе общие точки этих плоскостей (аксиома). Таким образом, две плоскости пересекаются по прямой (на рис. 28 Пересекающиеся плоскости образуют четыре двугранных угла. Если один из них прямой, тогда и остальные углы тоже прямые, а плоскости называются перпендикулярными. В качестве параллельных плоскостей на каждом шагу встречаем параллельные грани одного дома. Плоскости стен домов перпендикулярны плоскости земли. |
18) Взаимное расположение двух прямых на плоскости.Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий. |
Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.1)Прямые лежат в одной плоскости и не имеют общих точек - параллельные прямые. 2)Прямые лежат и одной плоскости и имеют одну общую точку - прямые пересекаются. 3)В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны). Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются. На рис. 26 прямая a лежит в плоскости Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.
На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты. |
2)Матрицы,действия над матрицами.Привести пример.Определение.Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы.Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца. А = |
20)Взаимное расположение прямой и плоскости. Для выяснения взаимного расположения прямой (x=b1t+x0; y=b2t+y0; z=b3t+z0) b(b1, b2, b3)-направляющий вектор прямой Ax+By+Cz+D=0 Чтобы найти точку пересечения прямой и плоскости, надо решить сист Ур-ий A(b1t+x0)+B(b2t+y0)+C(b3t+z0)+D=0; Ab1t+Ax0+Bb2t+By0+Cb3t+Cz0+D=0; (Ab1+Bb2+Cb3)t=-(Ax0+By0+Cz0+D). 1Случай: Ab1+Bb2+Cb3=0, определяет единственное решение, т.к. получаем конкретное значение параметра t, подставив которое в исходное Ур-е прямой получаем точки пересеч с данной плоскостью 2Случай: Пусть выражение Ab1+Bb2+Cb3=0, Ax0+By0+Cz0+D=0, т.к. левая часть не может быть равна правой, это говорит о том что прямая параллельна плоскости. 3Случай: Пусть Ab1+Bb2+Cb3=0, Ax0+By0+Cz0+D=0, Ур-ям удовлетворяют любые знач t след прямая лежит в плоскости. |
О М r1 r2 F1 F2 F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0) с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.Теорема.Фокусное расстояние и полуоси эллипса связаны соотношением:a2 = 2 + c2.Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r1 + r2 = 2 |
22)ГиперболаОпределение.Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
y M(x, y) r1 r2 x F1 a F2 c По определению r1 – r2= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.Выберем на гиперболе произвольную точку М(х, у). Тогда:
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
|
23)Парабола. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.Расположим начало координат посередине между фокусом и директрисой.
А у М(х, у) О F x
p/2 p/2 Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы.Из геометрических соотношений: AM = MF; AM = x + p/2;MF2 = y2 + (x – p/2)2 (x + p/2)2 = y2 + (x – p/2)2 x2 +xp + p2/4 = y2 + x2 – xp + p2/4 y2 = 2px Уравнение директрисы: x = -p/2. Пример. На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4. Из уравнения параболы получаем, что р = 4. r = x + p/2 = 4; следовательно:x = 2; y2 = 16; y = 4. Искомые точки: M1(2; 4), M2(2; -4). |
25)Общее ур-е линии второго порядкаКривые 2го порядка описываются с помощью общего ур-я: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где
а) Каноническое ур-е эллипса
Если a=b, то x2+b2=a2 - ур-е окружности. б) Ур-е гиперболы: x2/a2-y2/b2=1
в) ур-е параболы: y2=2px или y=ax2 г) ур-е сферы: x2+y2+z2=а2 (r2=(x-a)2+(y-b)2+(z-c)2) д) ур-е эллипса: x2/a2-y2/b2+z2/c2=1 |
О B a Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме. |
Основные действия с комплексными числами вытекают из действий с многочленами.1) Сложение и вычитание.
|


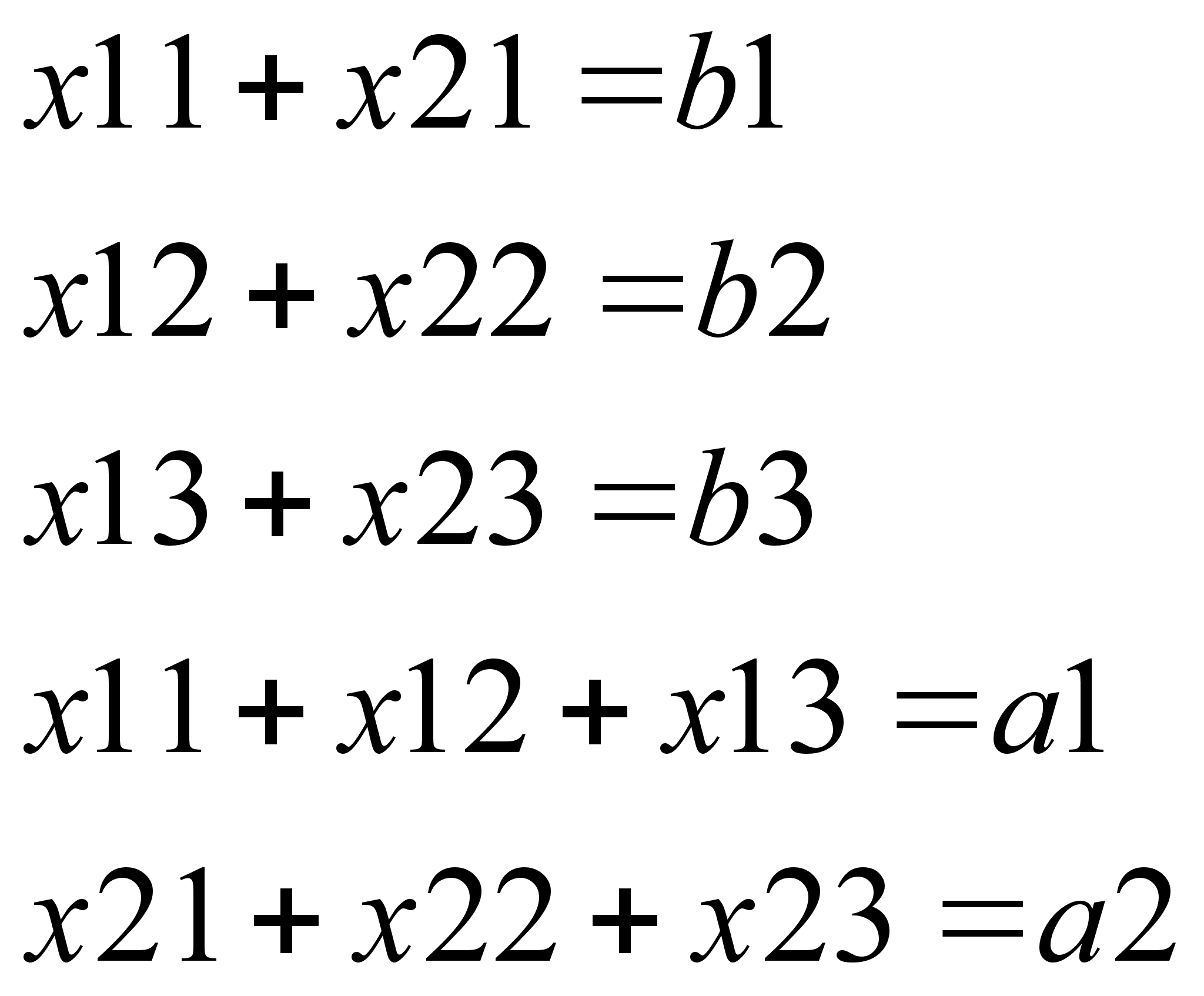
 Разделим обе части 1–го уравнения на a11
Разделим обе части 1–го уравнения на a11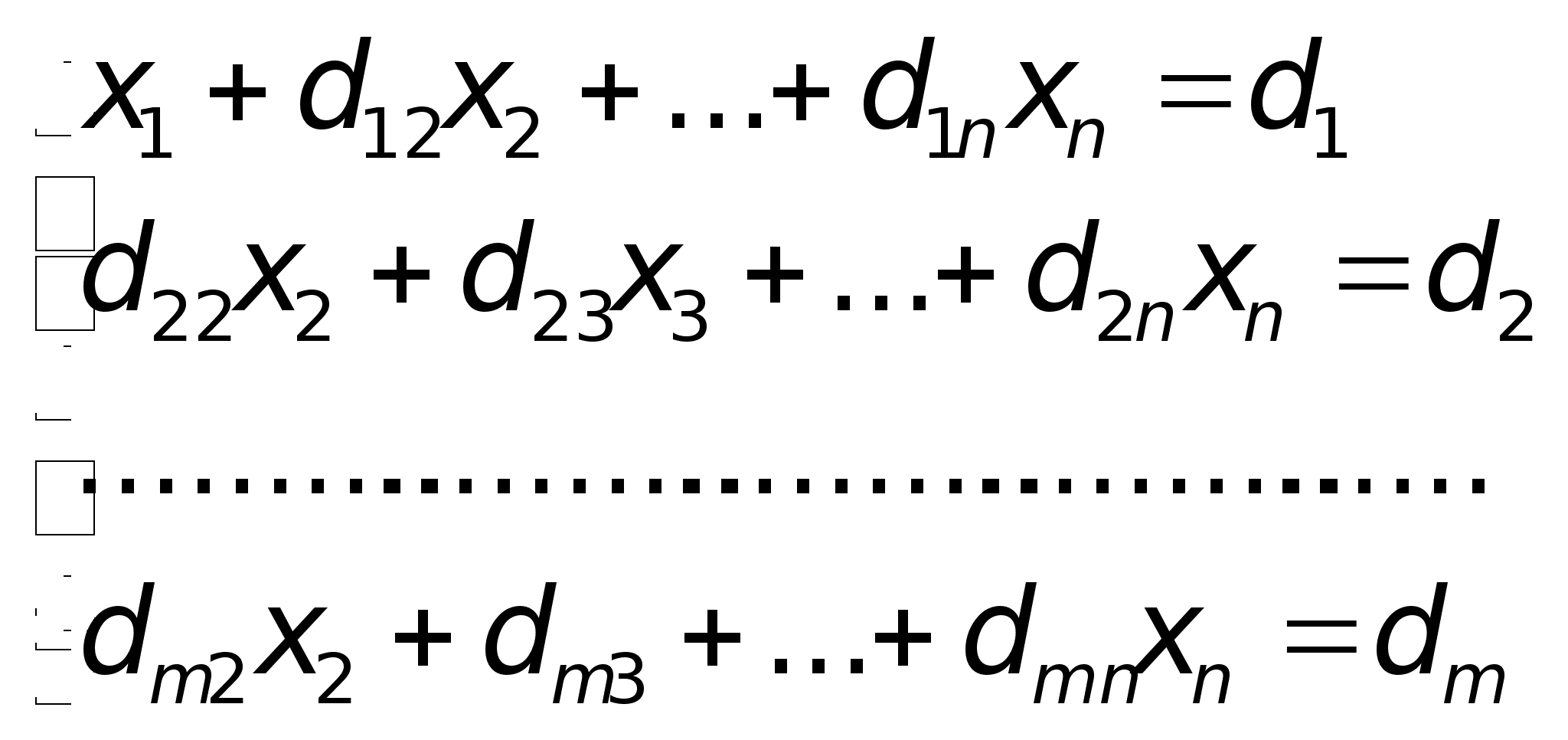 , где d1j = 1j/a11, j = 2, 3, …, +1 dij= aij – ai1d1ji = 2, 3, … , j = 2, 3, … , +1.Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.Пример. Решить систему линейных уравнений методом Гаусса.
, где d1j = 1j/a11, j = 2, 3, …, +1 dij= aij – ai1d1ji = 2, 3, … , j = 2, 3, … , +1.Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.Пример. Решить систему линейных уравнений методом Гаусса. Составим расширенную матрицу системы.* =
Составим расширенную матрицу системы.* =  Таким образом, исходная система может быть представлена в виде:
Таким образом, исходная система может быть представлена в виде: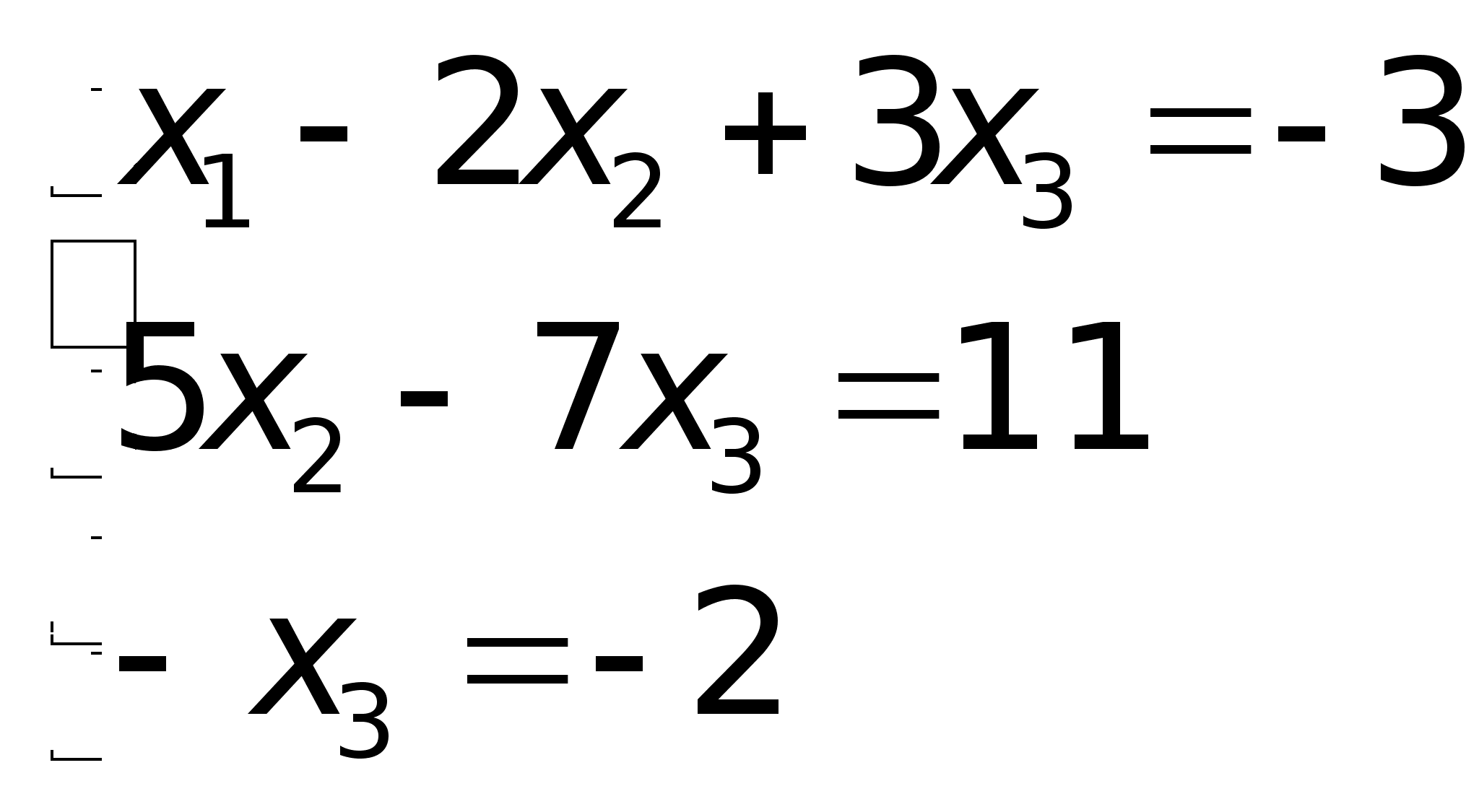 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.Пример. Решить систему методом Гаусса.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.Пример. Решить систему методом Гаусса.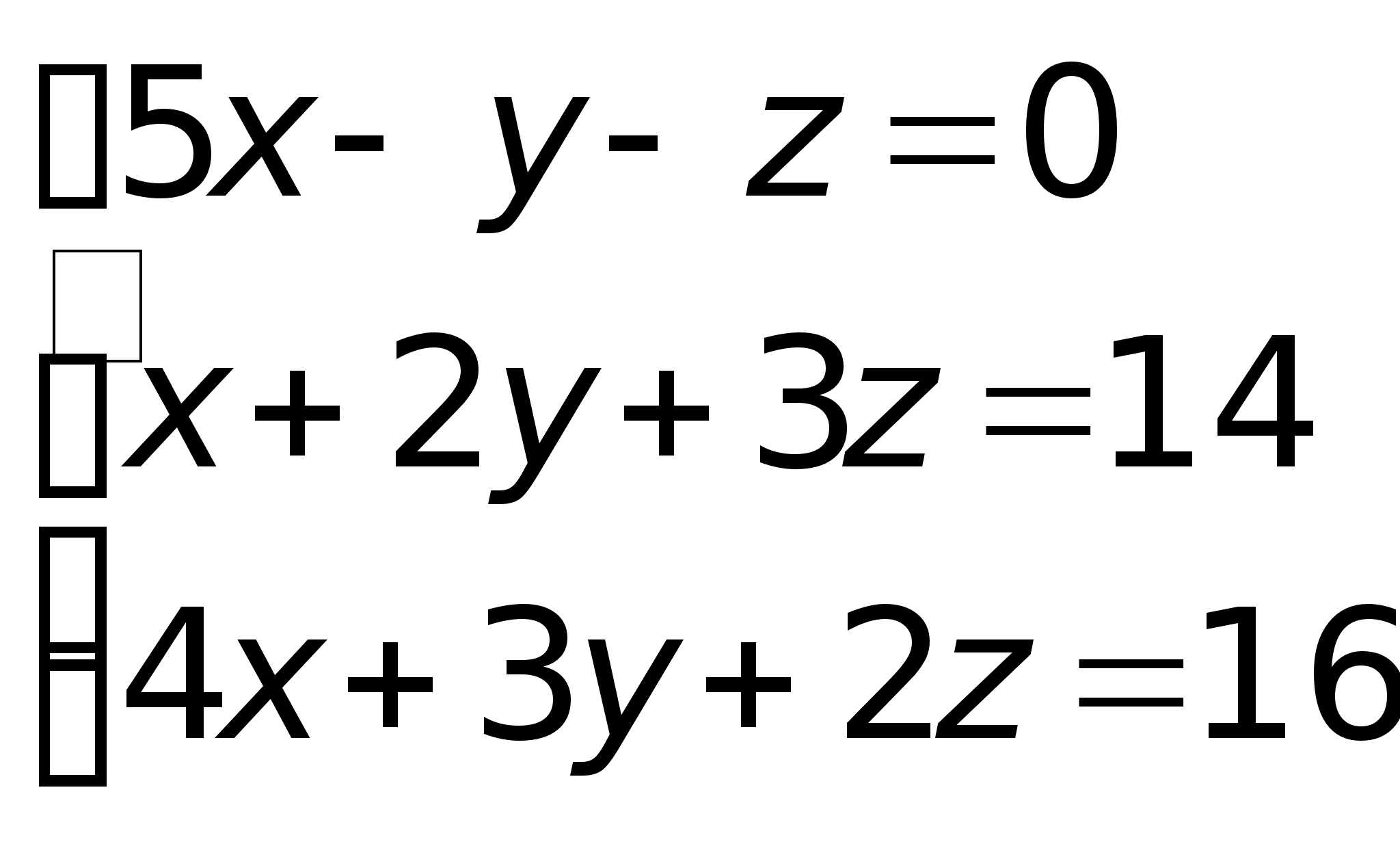 Составим расширенную матрицу системы.
Составим расширенную матрицу системы.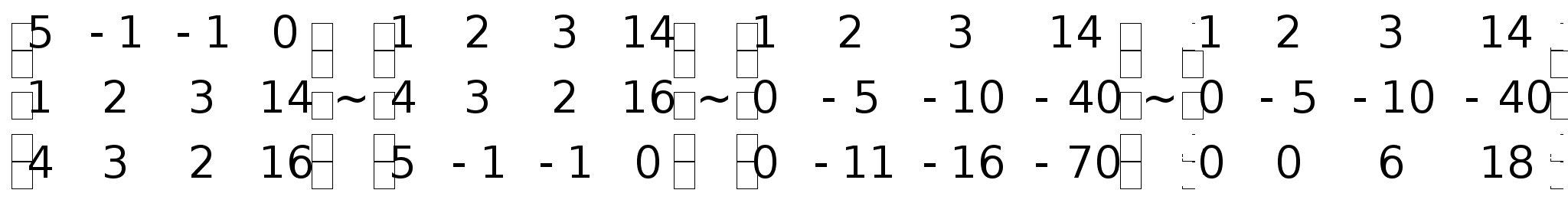 Таким образом, исходная система может быть представлена в виде:
Таким образом, исходная система может быть представлена в виде: , откуда получаем: z = 3; y = 2; x = 1.Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом.Для самостоятельного решения:
, откуда получаем: z = 3; y = 2; x = 1.Полученный ответ совпадает с ответом, полученным для данной системы методом Крамера и матричным методом.Для самостоятельного решения: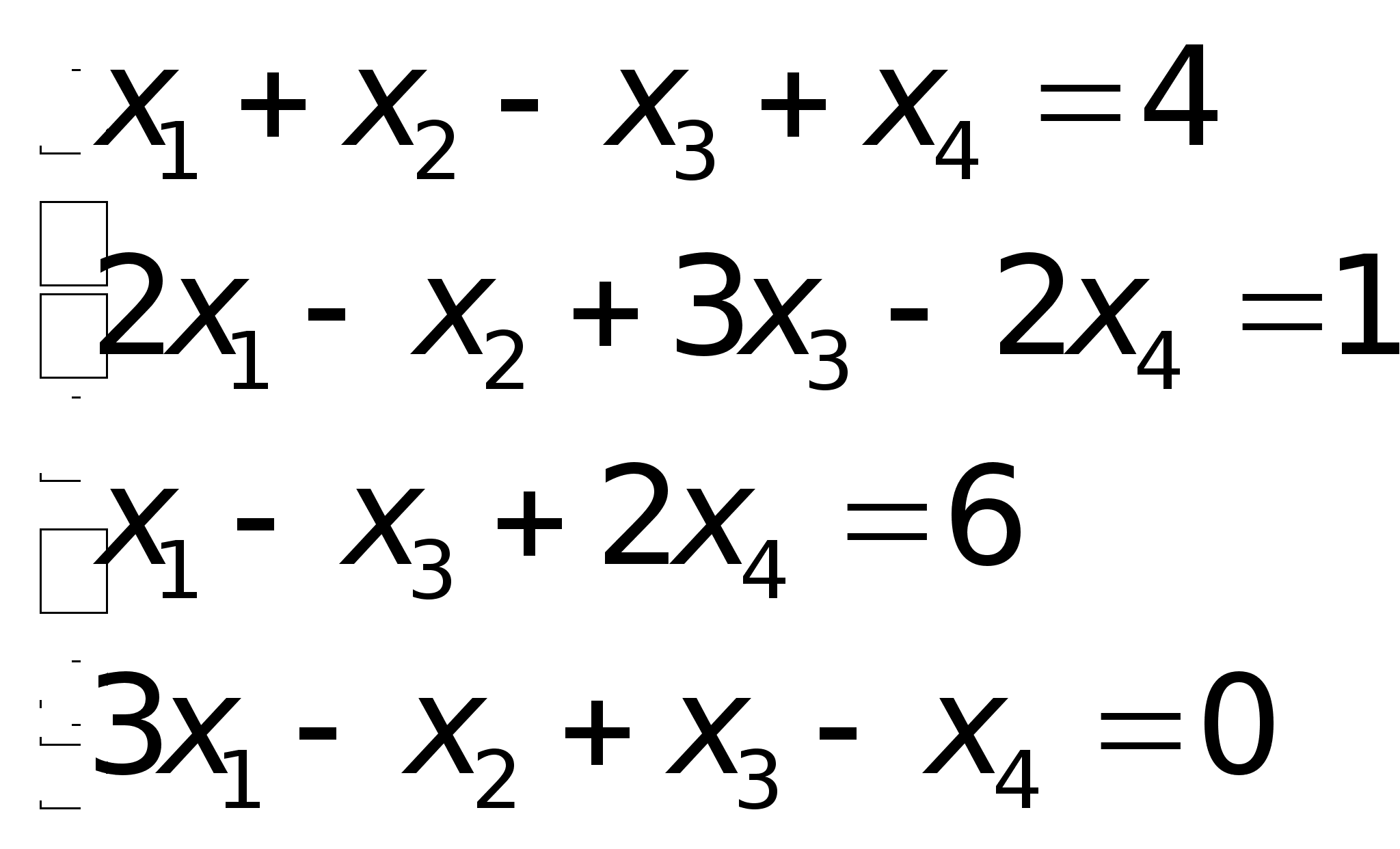 Ответ: {1, 2, 3, 4}.
Ответ: {1, 2, 3, 4}.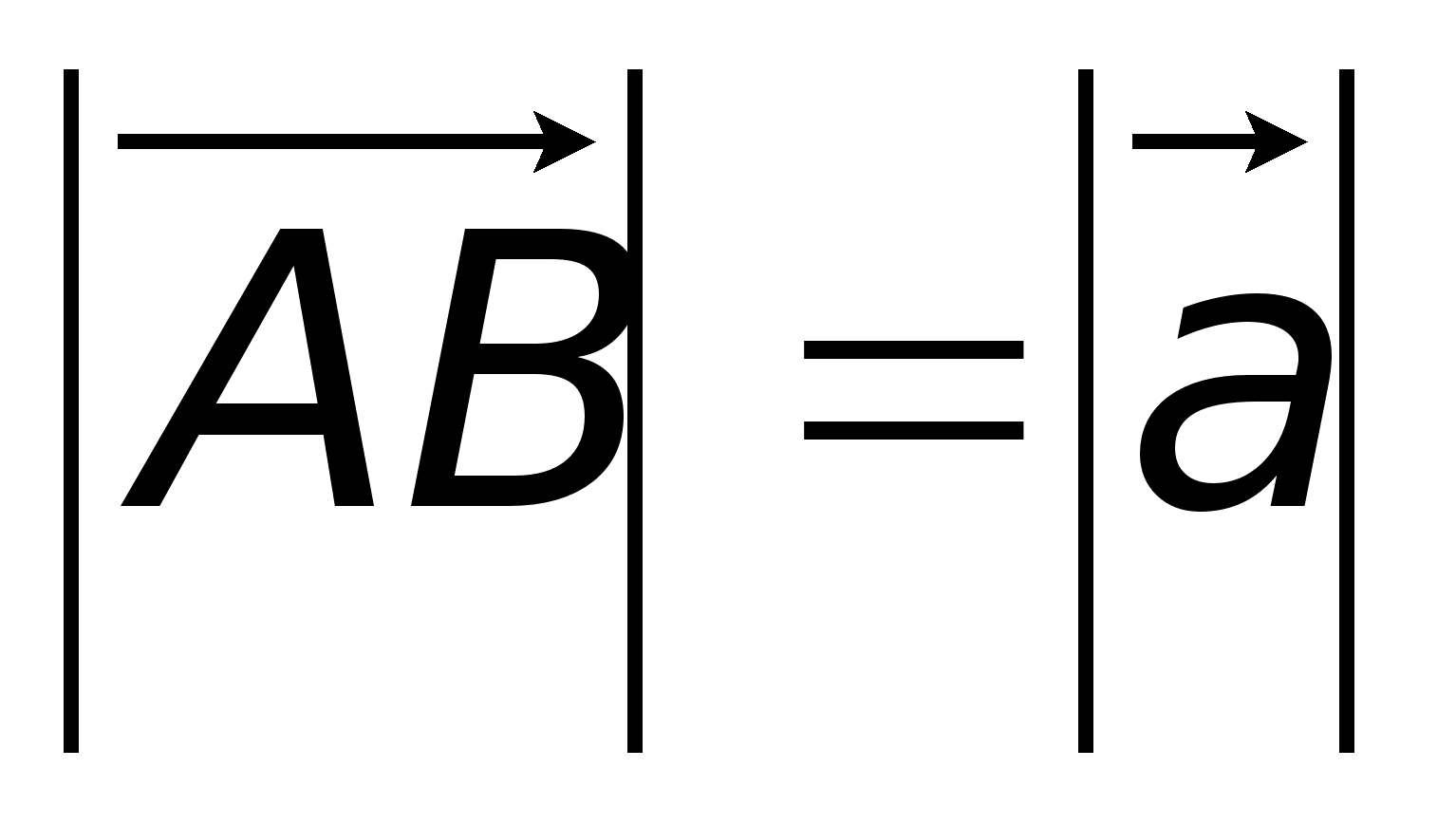 Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны. Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.Определение.Линейными операциями над векторами называется сложение и умножение на число.Суммой векторов является вектор -
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны. Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.Определение.Линейными операциями над векторами называется сложение и умножение на число.Суммой векторов является вектор -  Произведение -
Произведение -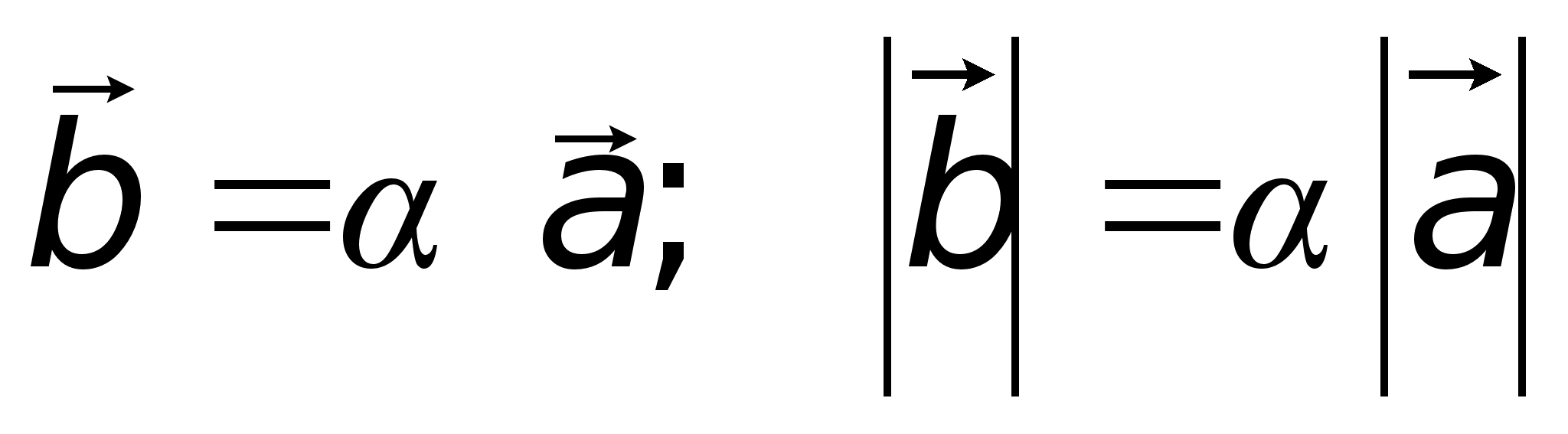 , при этом
, при этом  коллинеарен
коллинеарен  .Вектор
.Вектор  тогда
тогда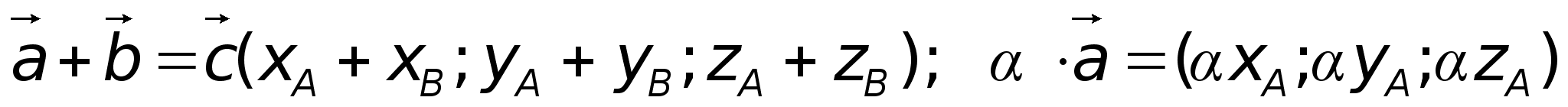
 и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними. ) =
) = 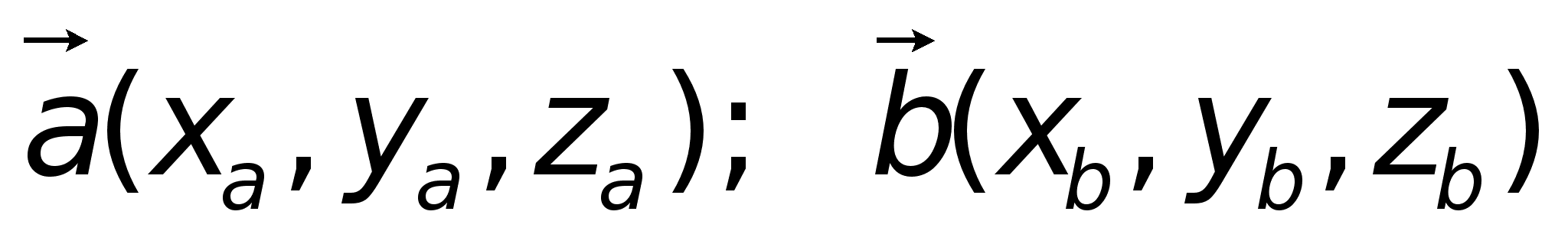 в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то ;Пример. Найти (5
;Пример. Найти (5 10
10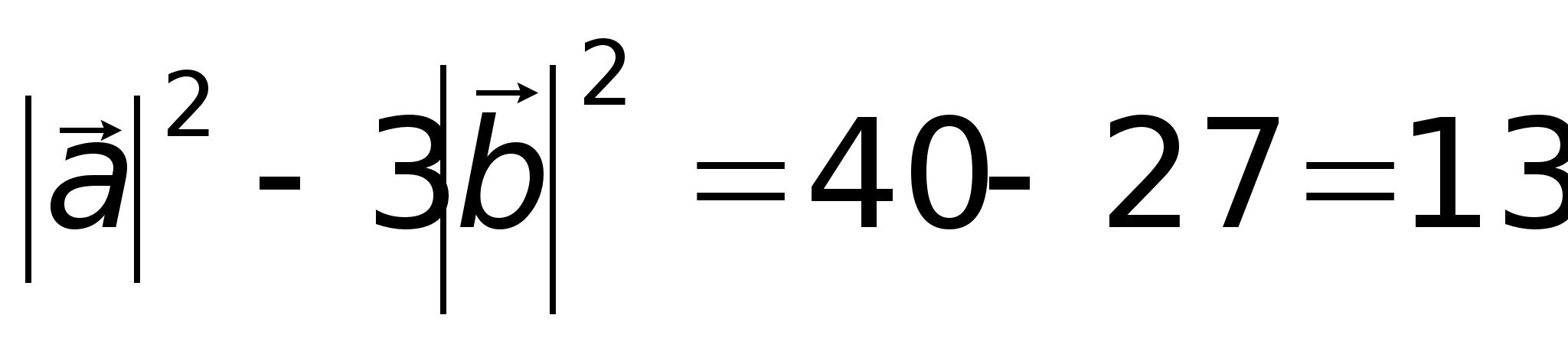 , т.к.
, т.к.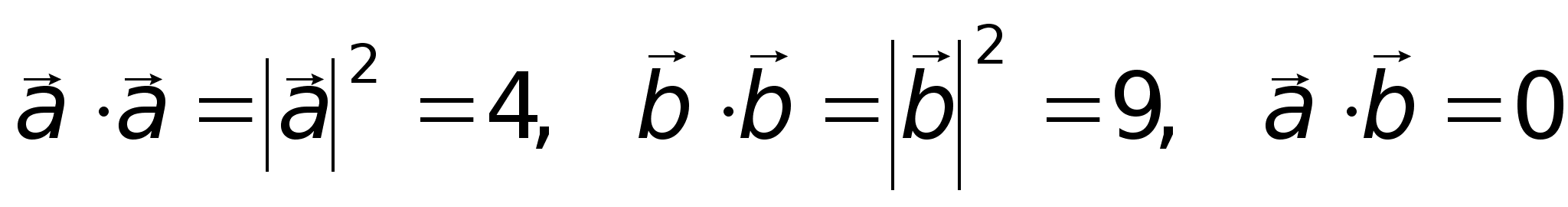 .
. и
и  называется вектор
называется вектор  , удовлетворяющий следующим условиям:1)
, удовлетворяющий следующим условиям:1) 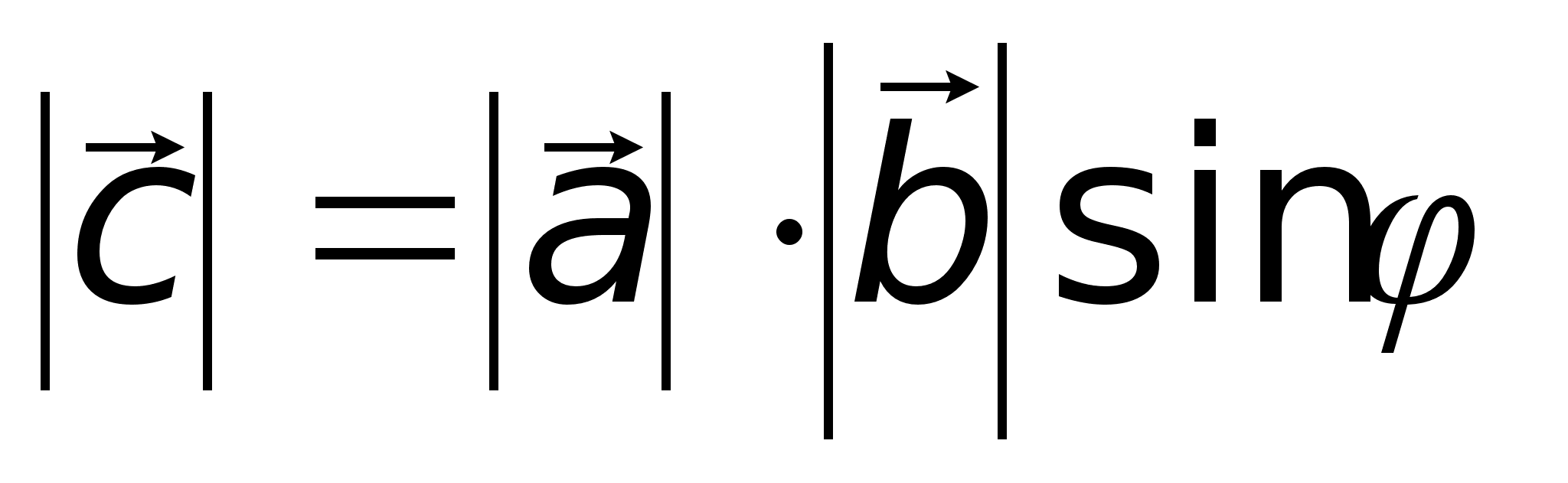 , где
, где 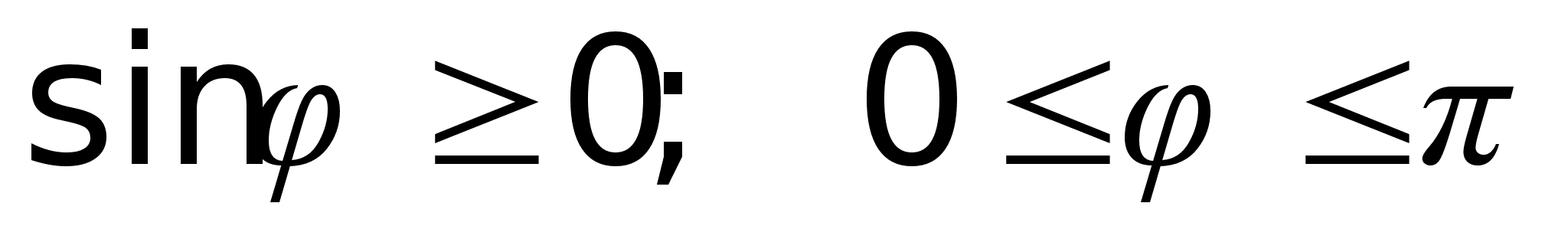 2) вектор
2) вектор 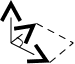 )
)  или
или .
.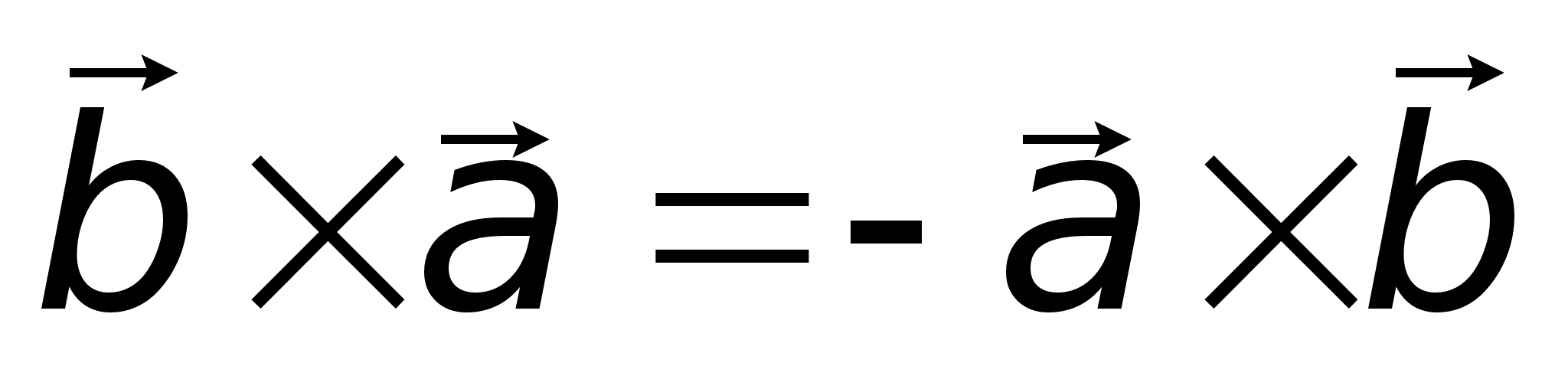 ;2)
;2)  , если
, если  ) =
) =  , то
, то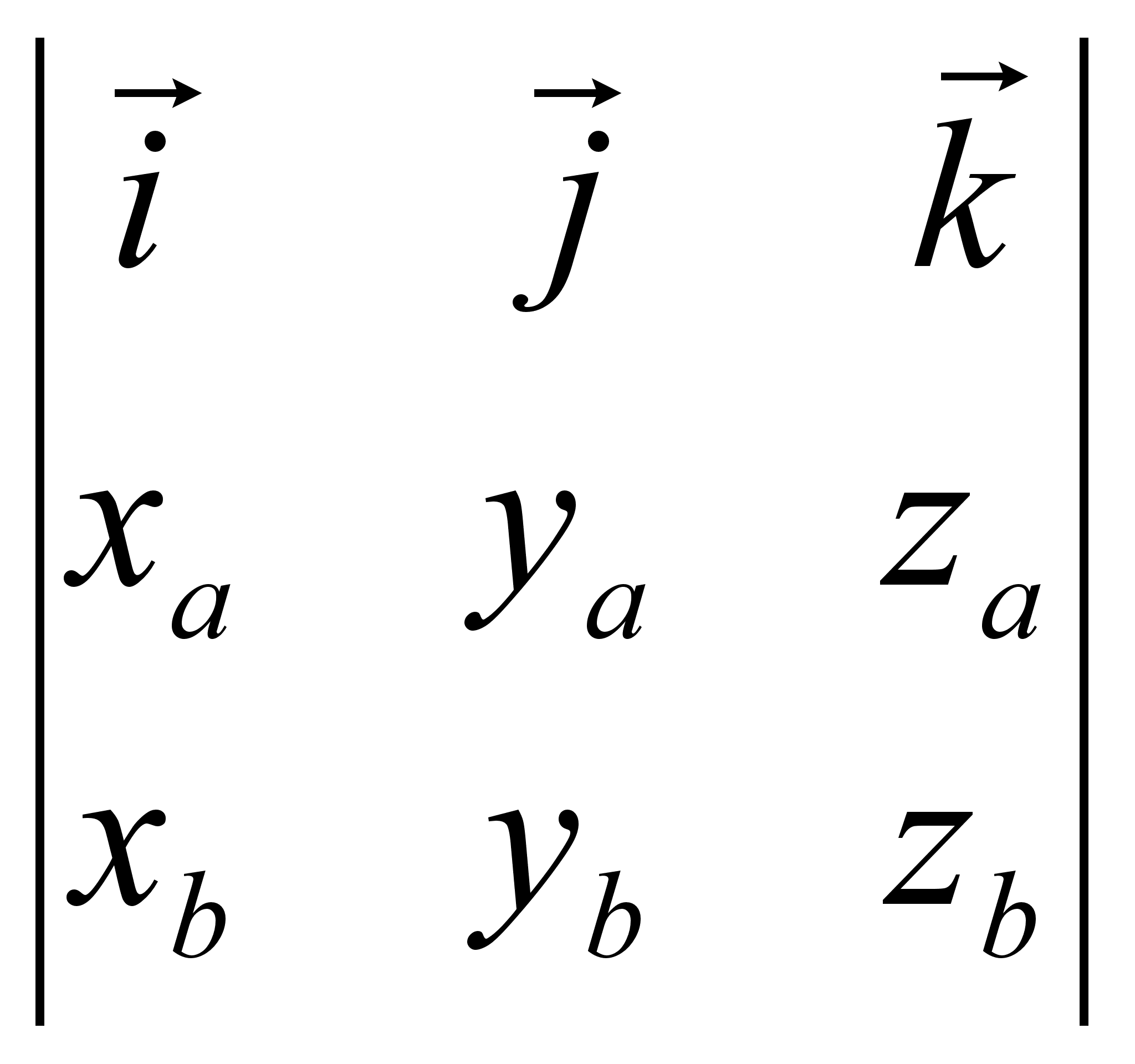 6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах 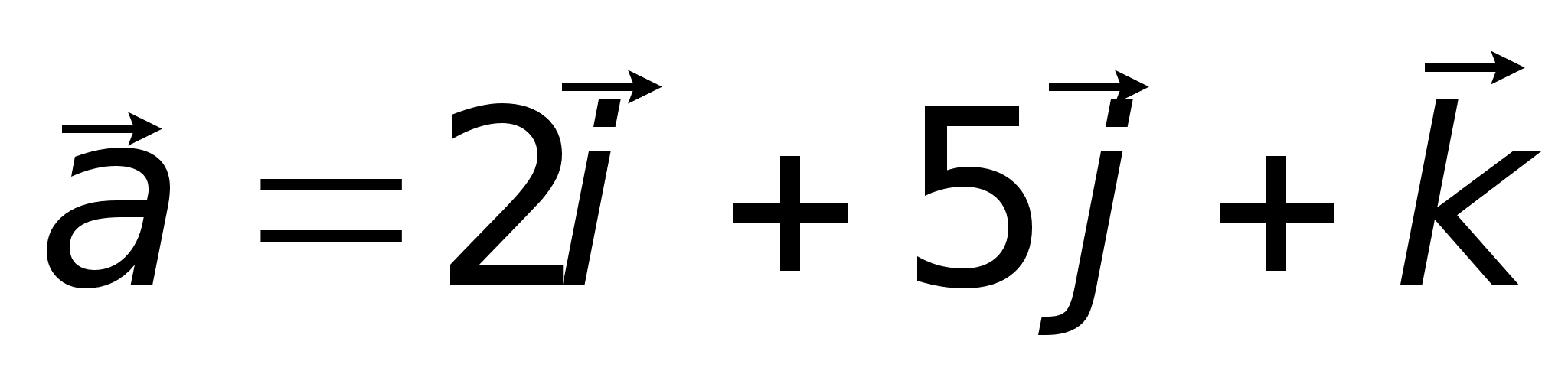 и
и 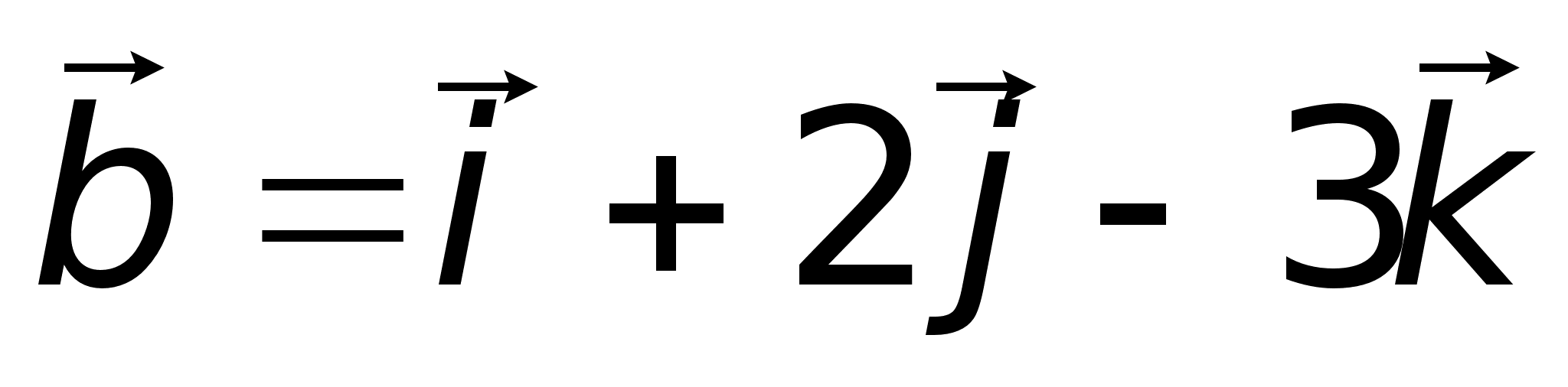 .
.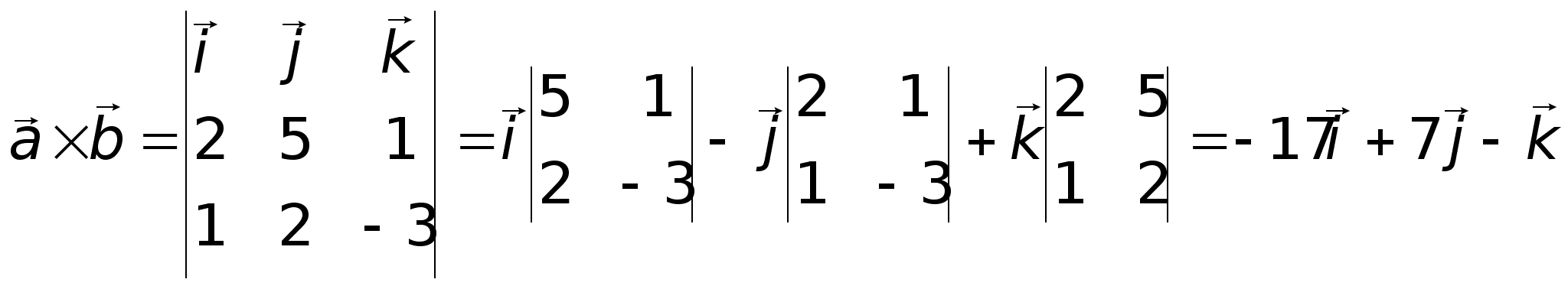 .
. ,
, 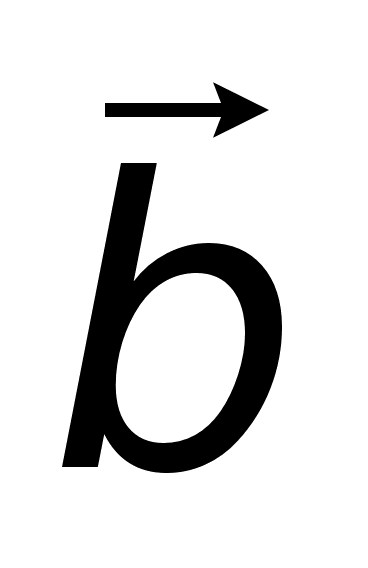 и
и  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 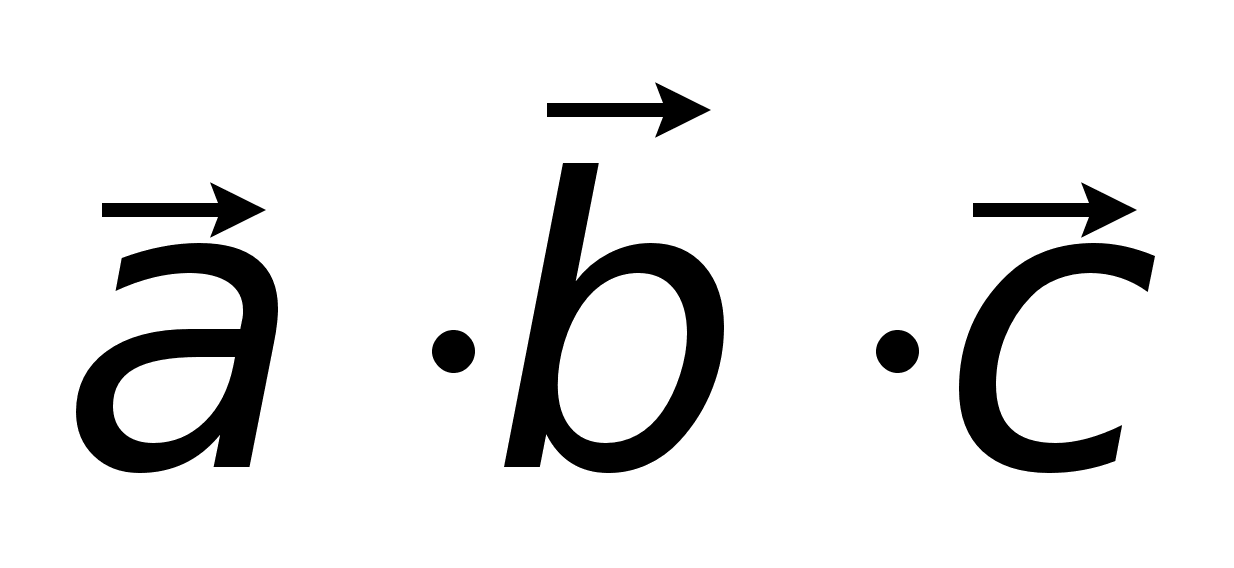 или (
или (
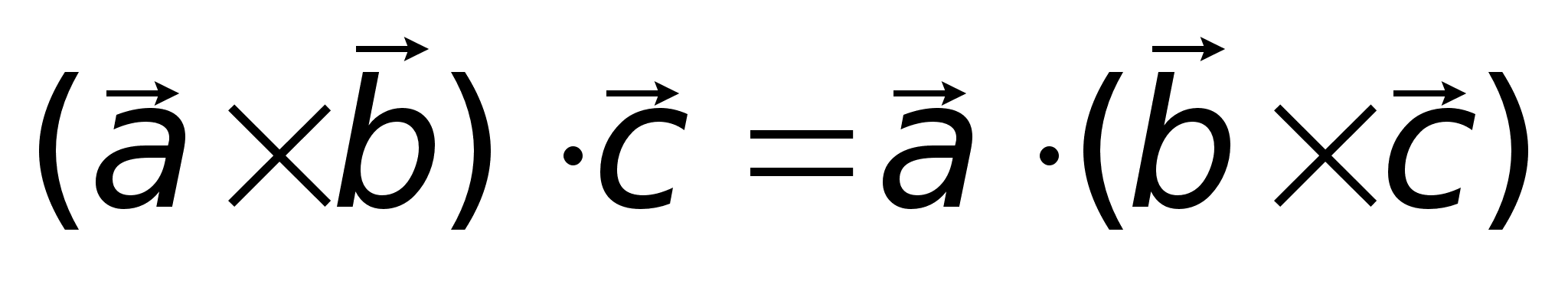 3)
3)
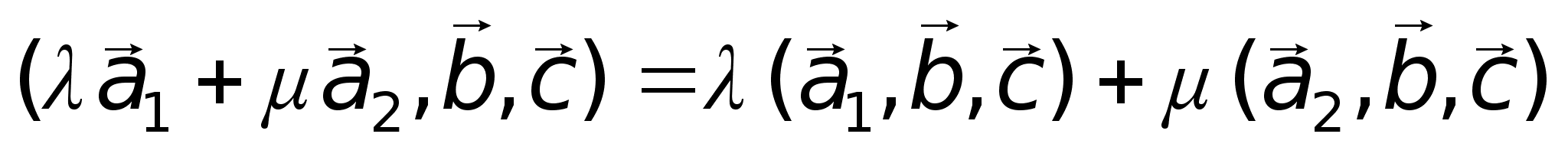 5) Объем треугольной пирамиды, образованной векторами
5) Объем треугольной пирамиды, образованной векторами 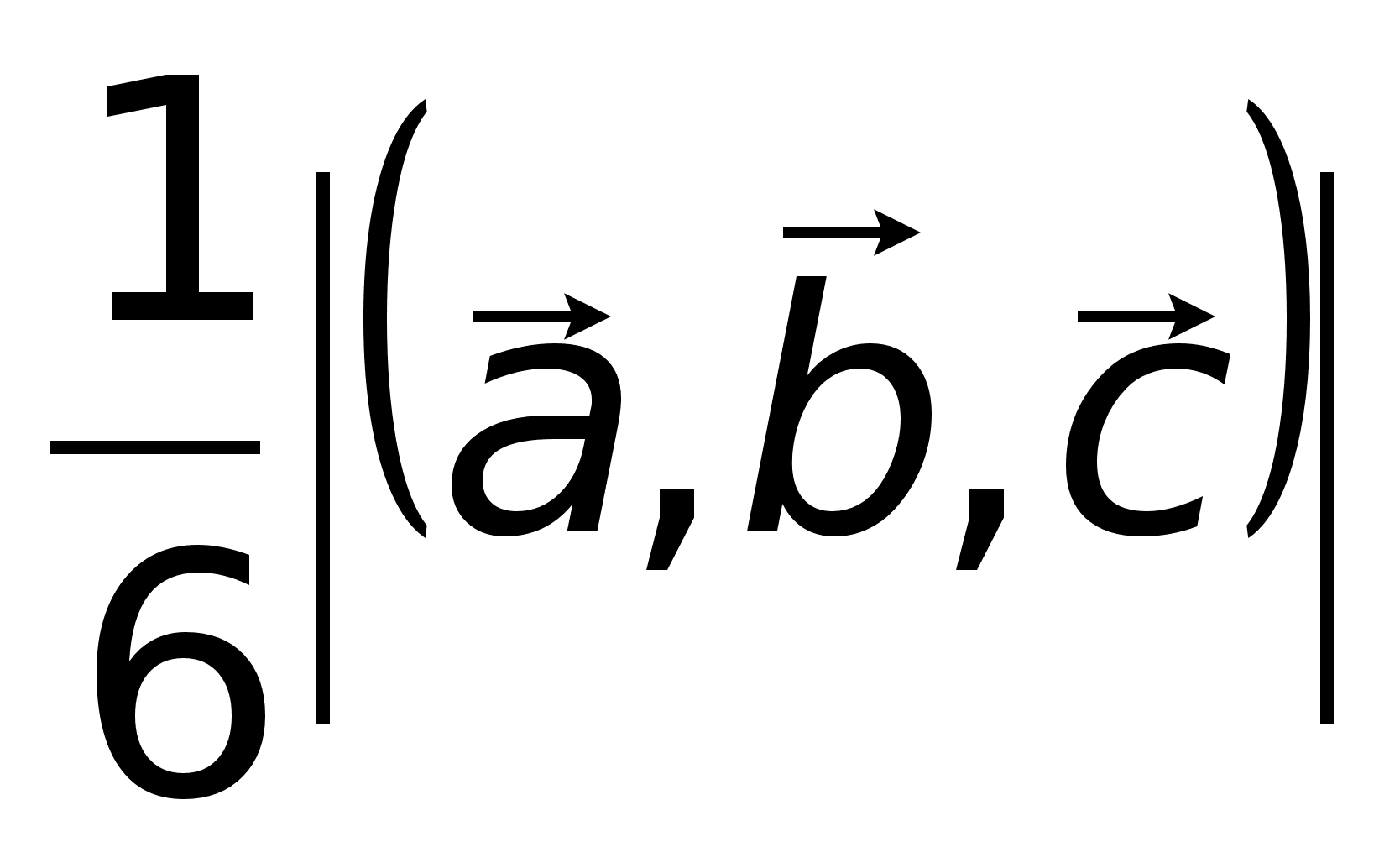 6)Если
6)Если  ,
,  , то
, то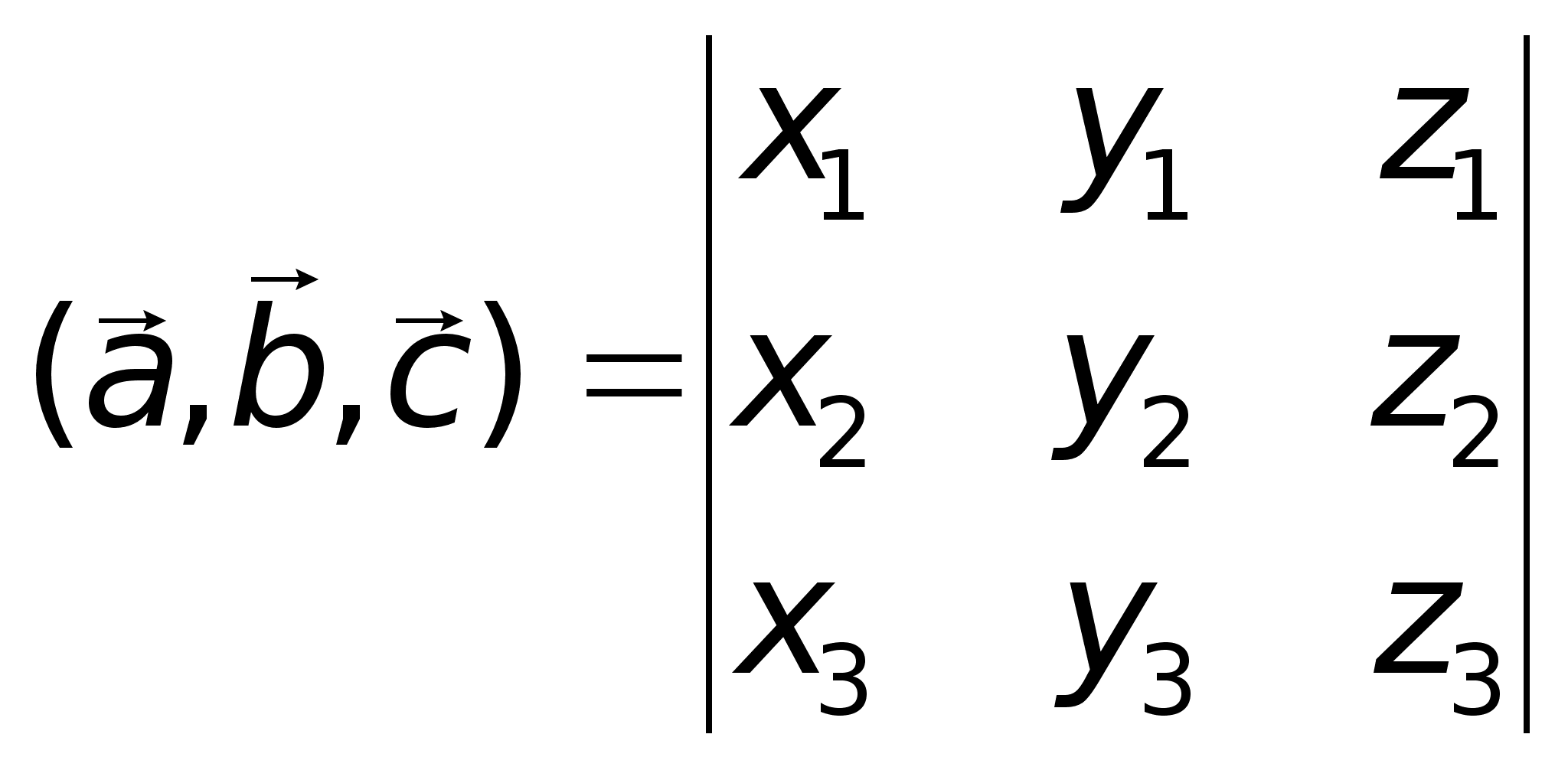 Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.Найдем координаты векторов:
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.Найдем координаты векторов:  Найдем смешанное произведение полученных векторов:
Найдем смешанное произведение полученных векторов: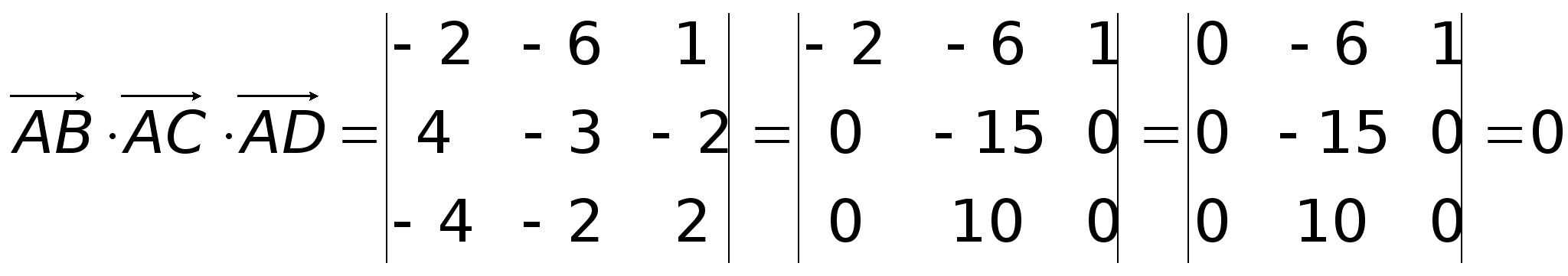 ,Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).Найдем координаты векторов:
,Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).Найдем координаты векторов: 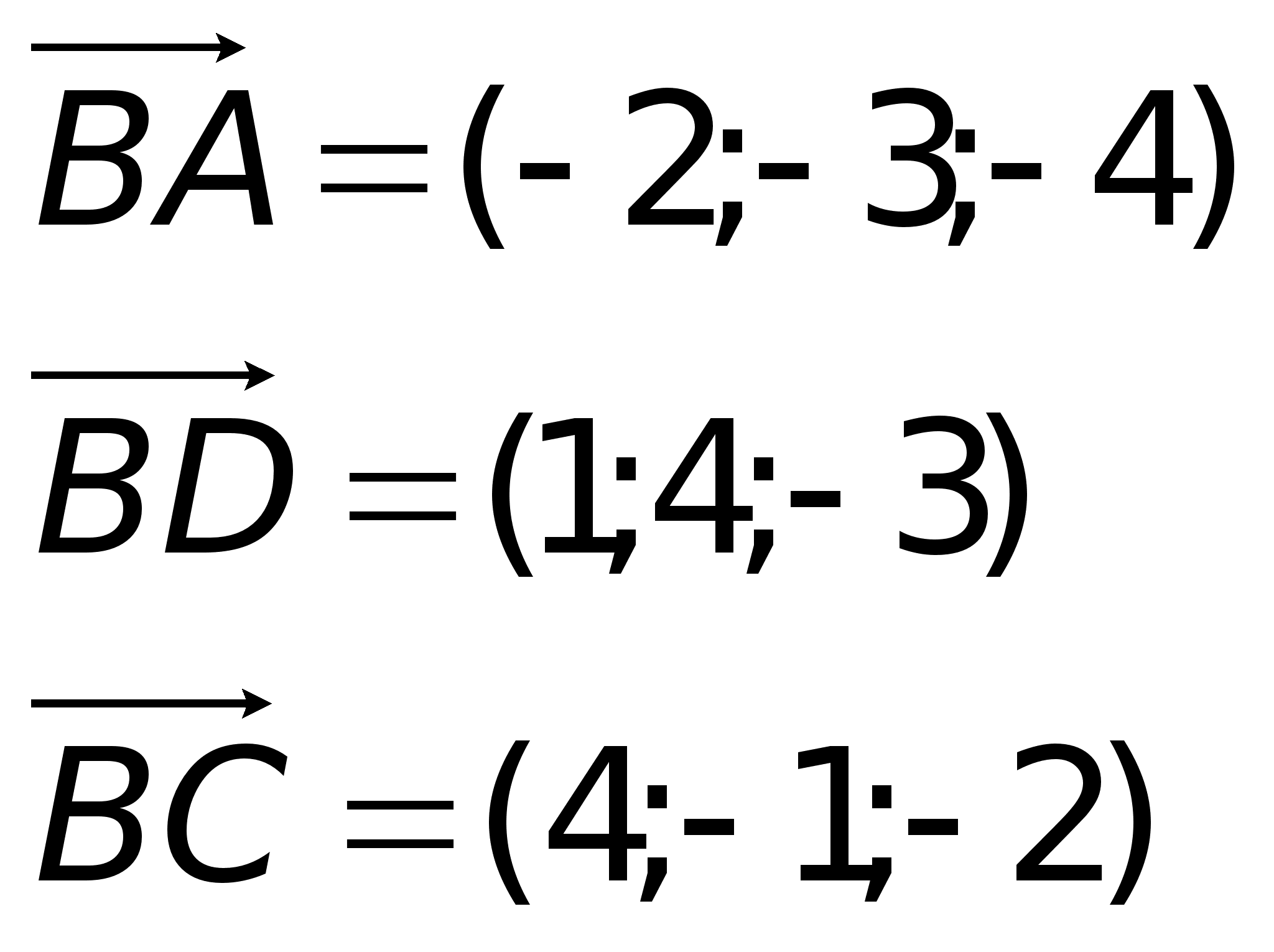 Объем пирамиды
Объем пирамиды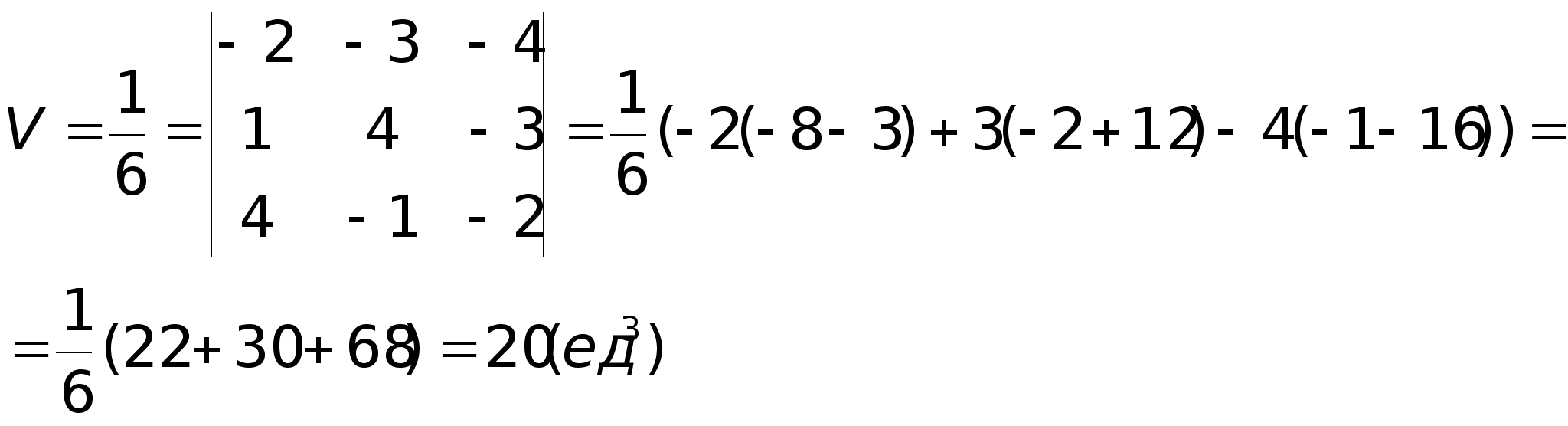

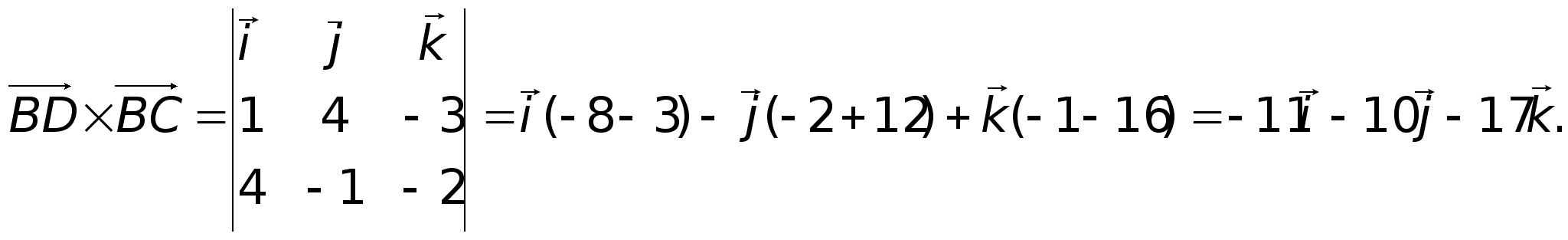
 (ед2)Т.к. V =
(ед2)Т.к. V = 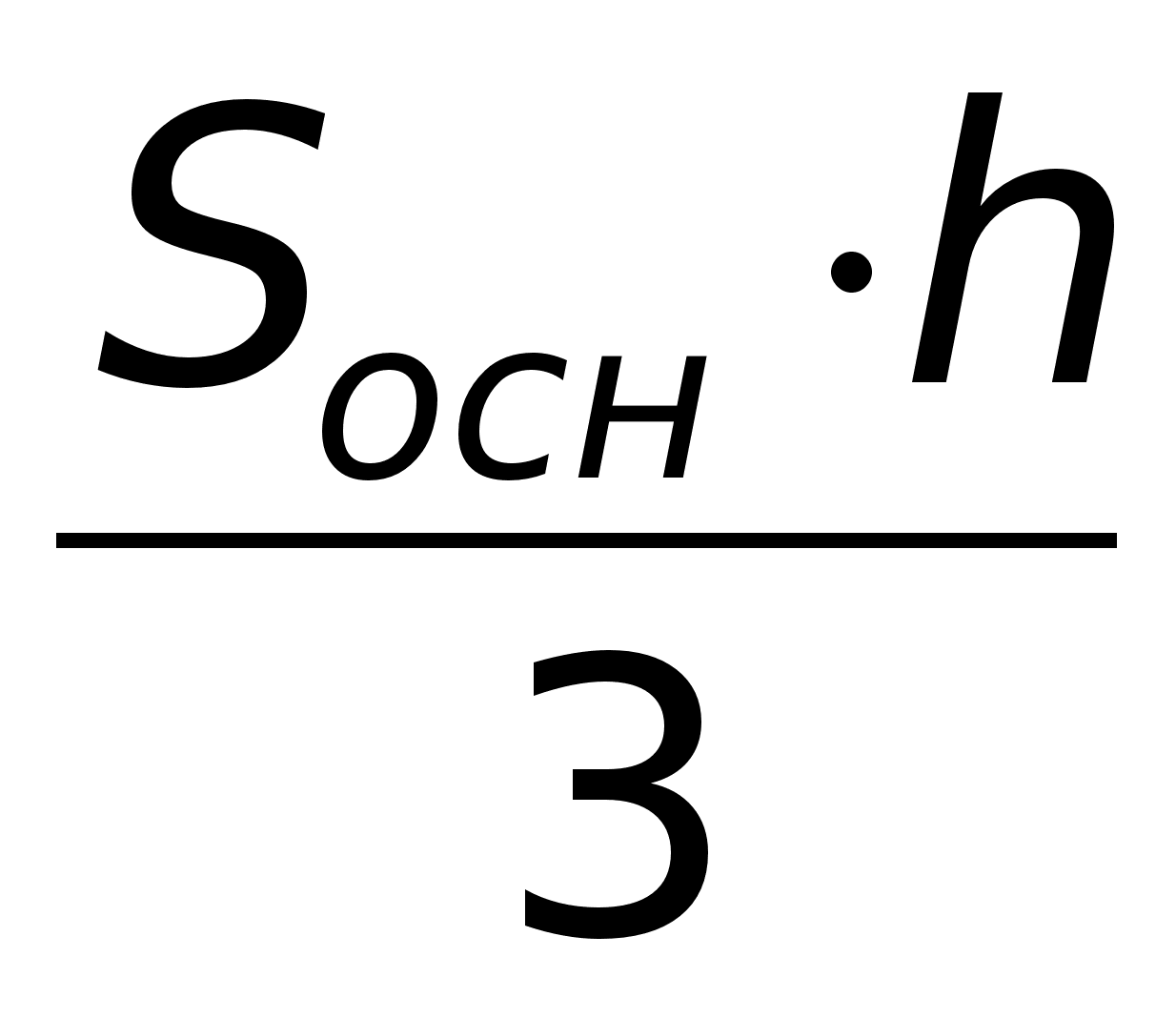 ; (ед)
; (ед)

 + D = 0, где
+ D = 0, где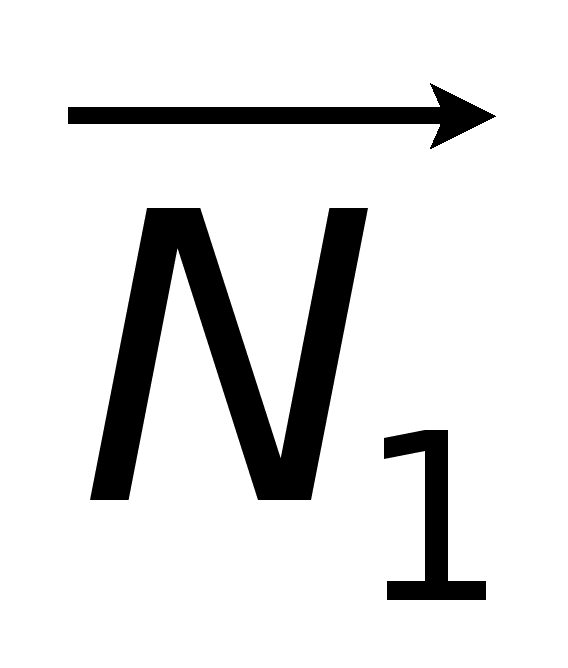

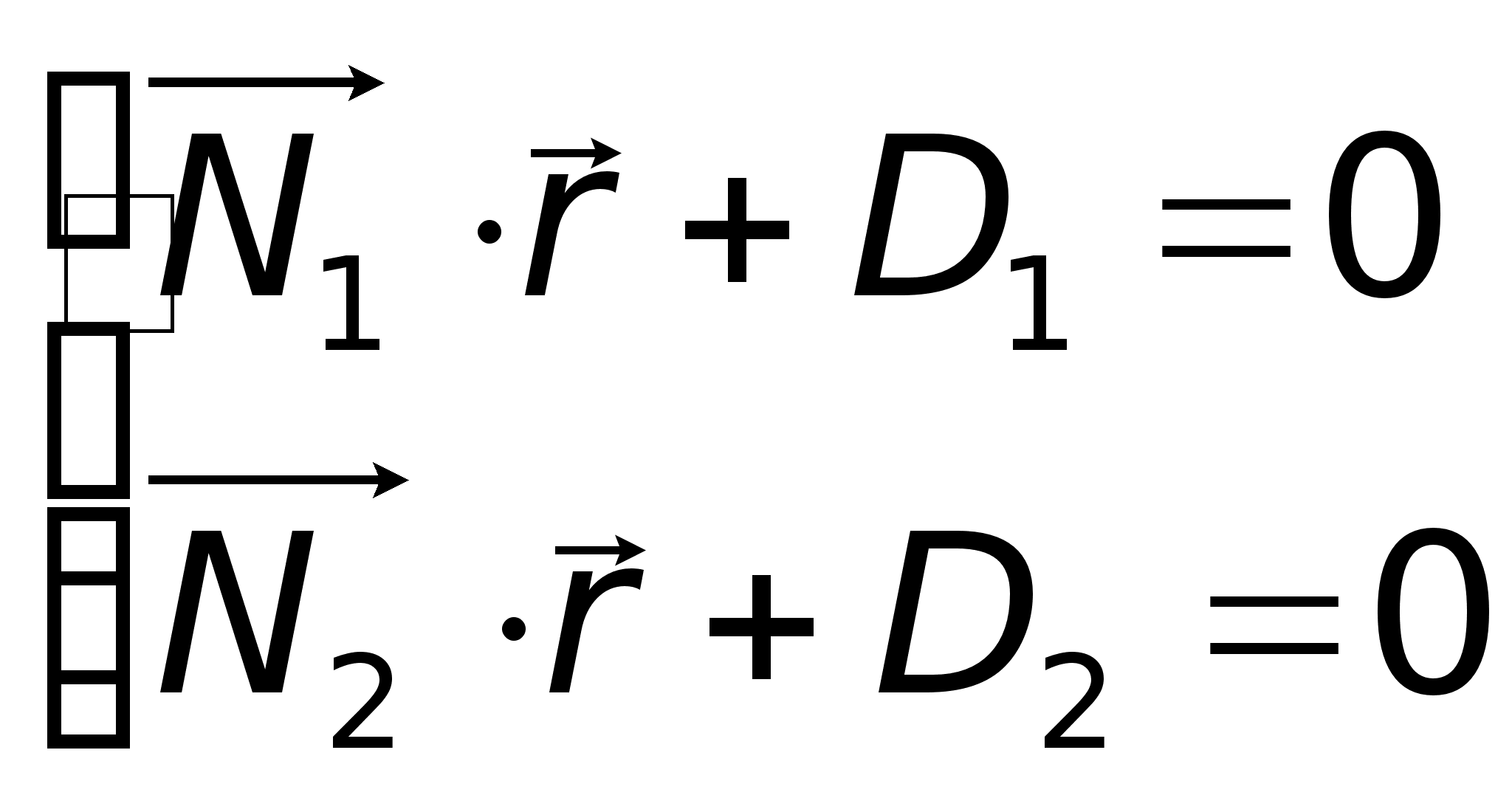 Общие уравнения прямой в координатной форме:
Общие уравнения прямой в координатной форме: Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.Для этого надо найти произвольную точку прямой и числа m, n, p.При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.
Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.Для этого надо найти произвольную точку прямой и числа m, n, p.При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.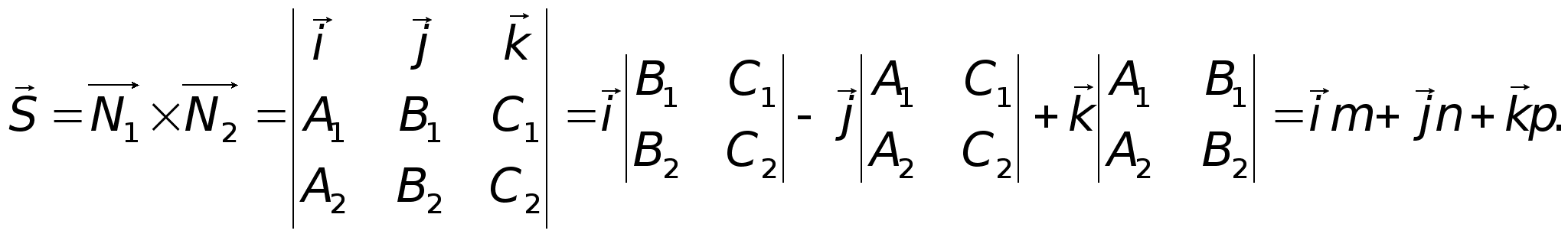 Пример. Найти каноническое уравнение, если прямая задана в виде:
Пример. Найти каноническое уравнение, если прямая задана в виде: Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.
Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.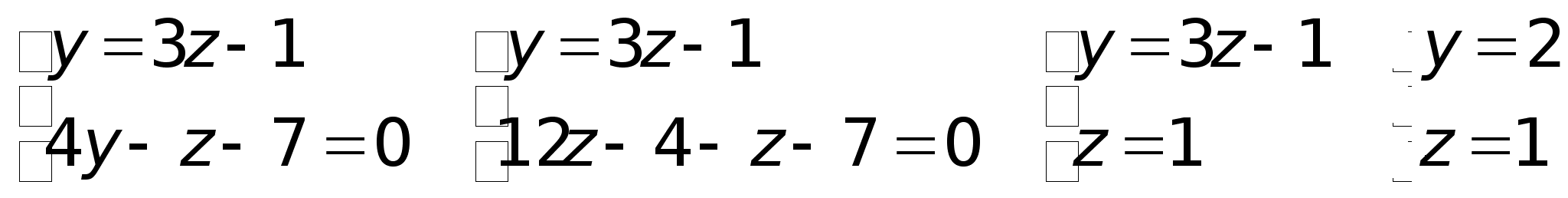 , т.е. А(0, 2, 1).Находим компоненты направляющего вектора прямой.
, т.е. А(0, 2, 1).Находим компоненты направляющего вектора прямой.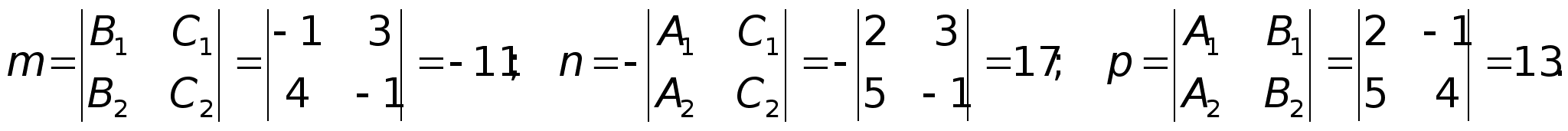 Тогда канонические уравнения прямой:
Тогда канонические уравнения прямой: Пример. Привести к каноническому виду уравнение прямой, заданное в виде:
Пример. Привести к каноническому виду уравнение прямой, заданное в виде: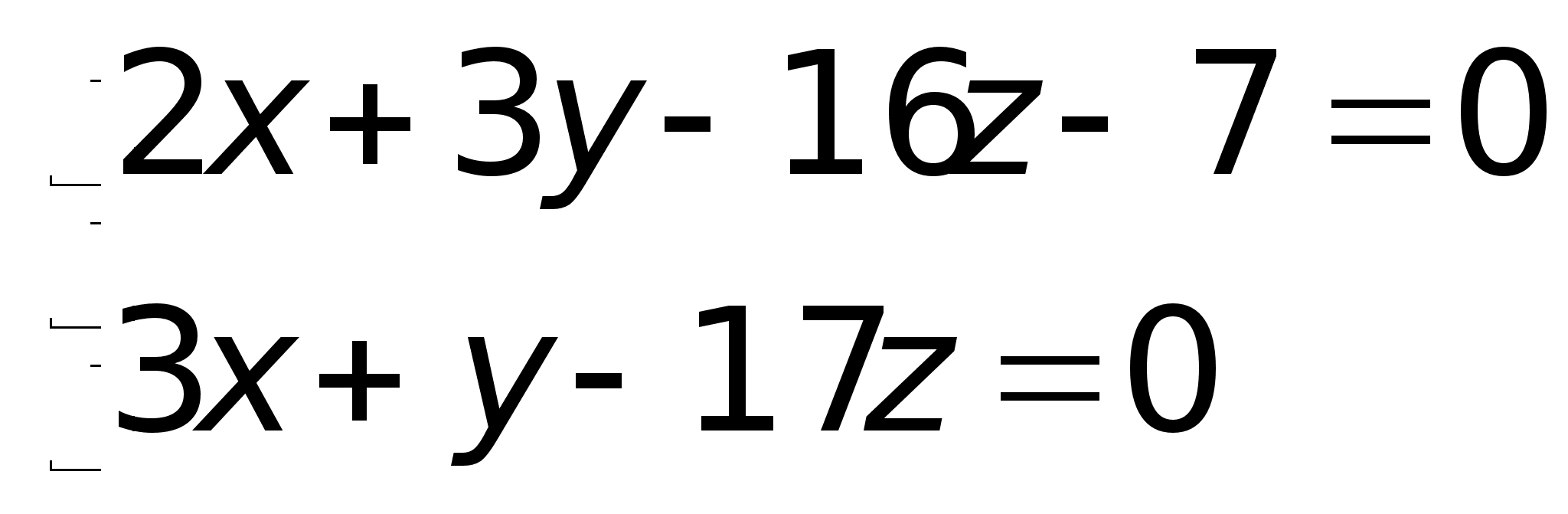 Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:
Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда: ;2x – 9x – 7 = 0; x = -1; y = 3; Получаем: A(-1; 3; 0).Направляющий вектор прямой:
;2x – 9x – 7 = 0; x = -1; y = 3; Получаем: A(-1; 3; 0).Направляющий вектор прямой: 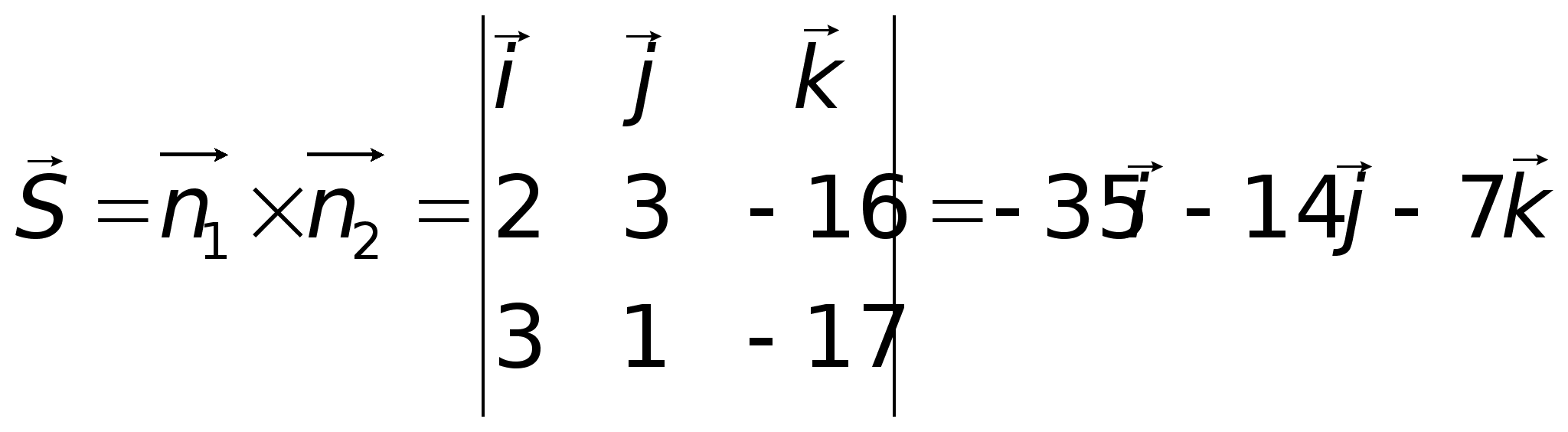 .Итого:
.Итого: 
 ||
||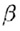 ).
).
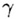 пересекаются по прямой a, a
пересекаются по прямой a, a 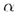 , а прямая с пересекает
, а прямая с пересекает 
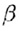 указана прямая a1 || b).
указана прямая a1 || b). 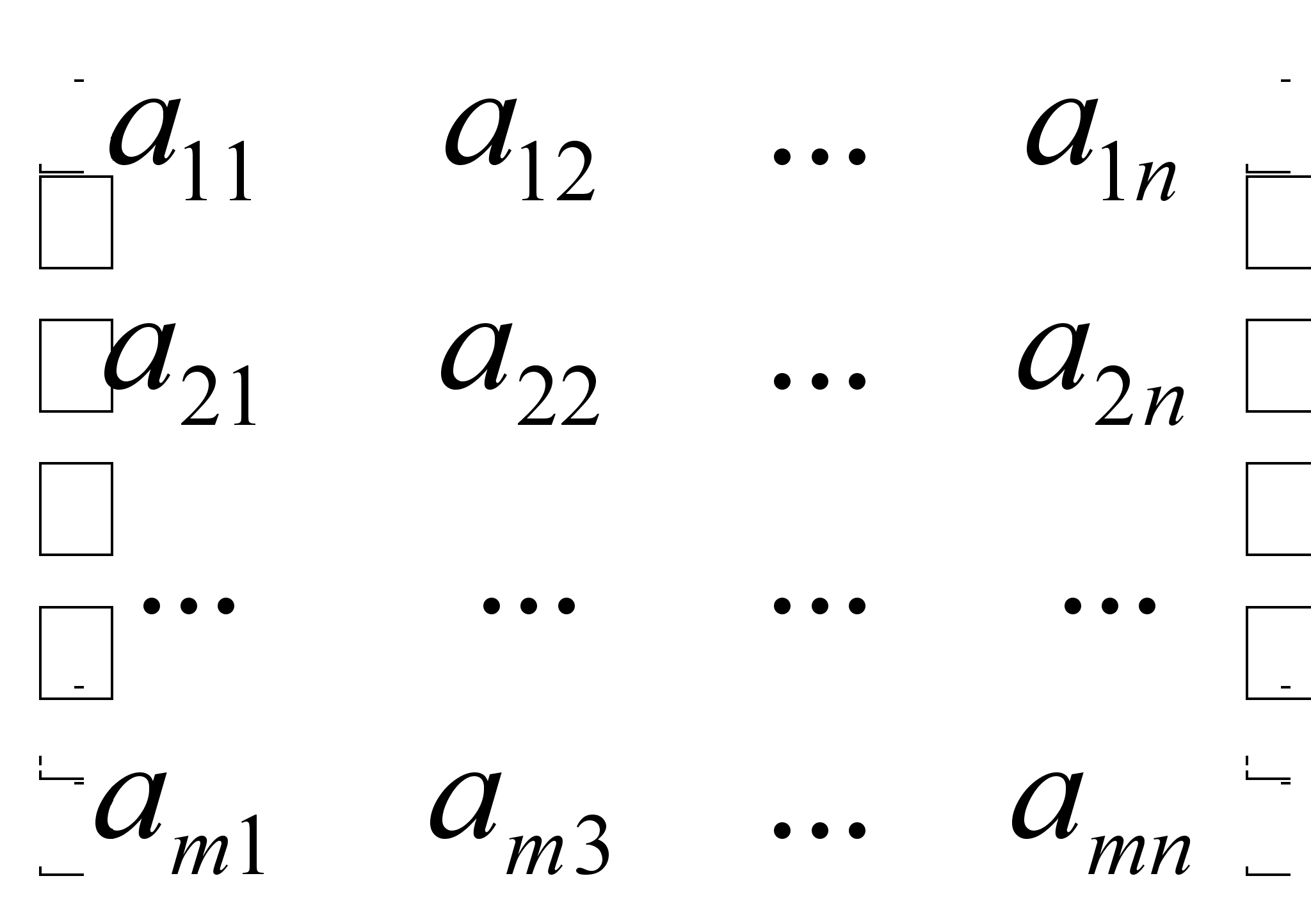 Основные действия над матрицами.Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.Определение. Матрица вида:
Основные действия над матрицами.Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.Определение. Матрица вида: = E,называется единичной матрицей.Определение. Если amn = anm, то матрица называется симметрической.Пример.
= E,называется единичной матрицей.Определение. Если amn = anm, то матрица называется симметрической.Пример. - симметрическая матрицаОпределение. Квадратная матрица вида
- симметрическая матрицаОпределение. Квадратная матрица вида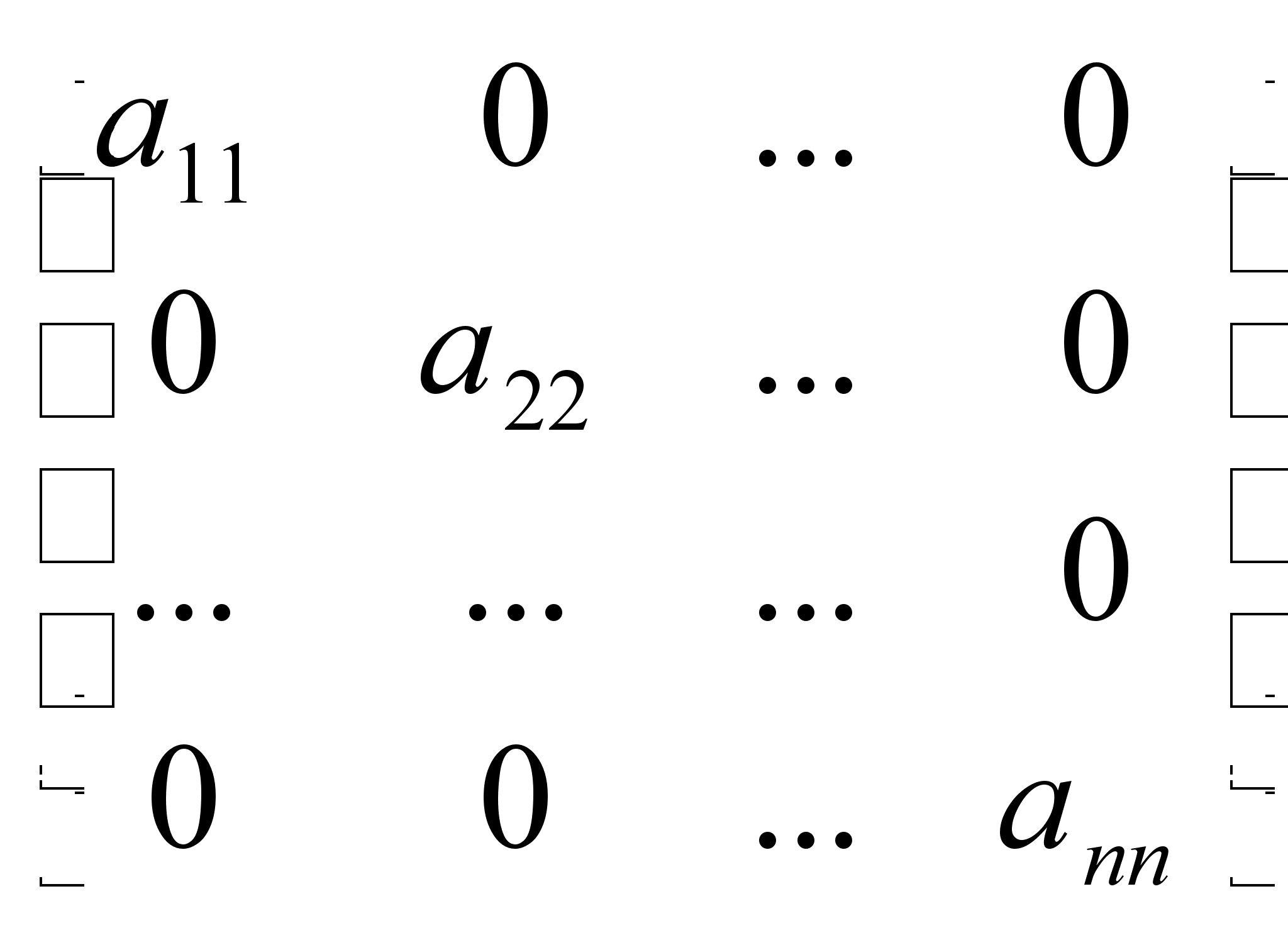 называется диагональной матрицей. Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:Определение.Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.cij = aij
называется диагональной матрицей. Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:Определение.Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.cij = aij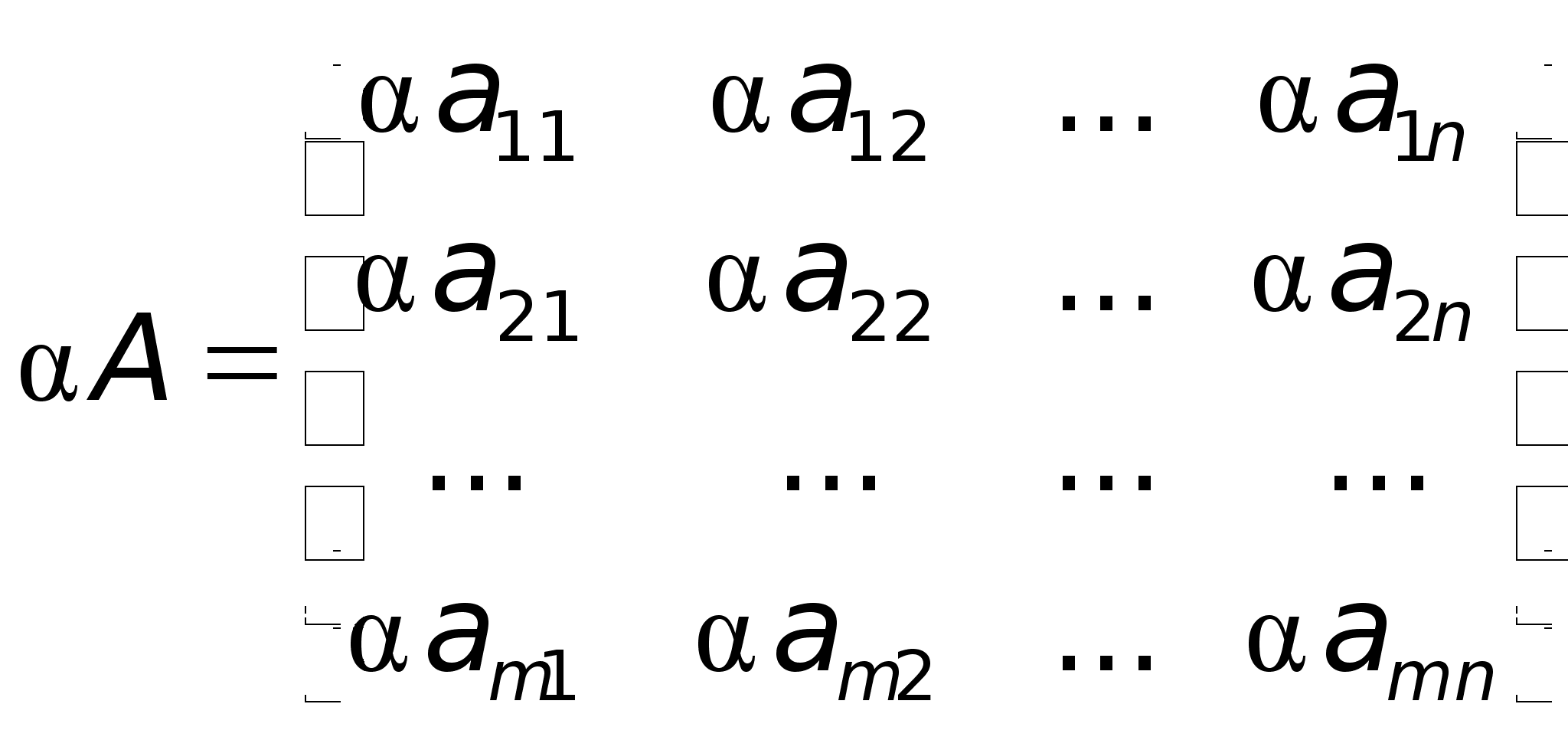
 ; B =
; B =  , найти 2А + В.2А =
, найти 2А + В.2А =  , 2А + В =
, 2А + В = 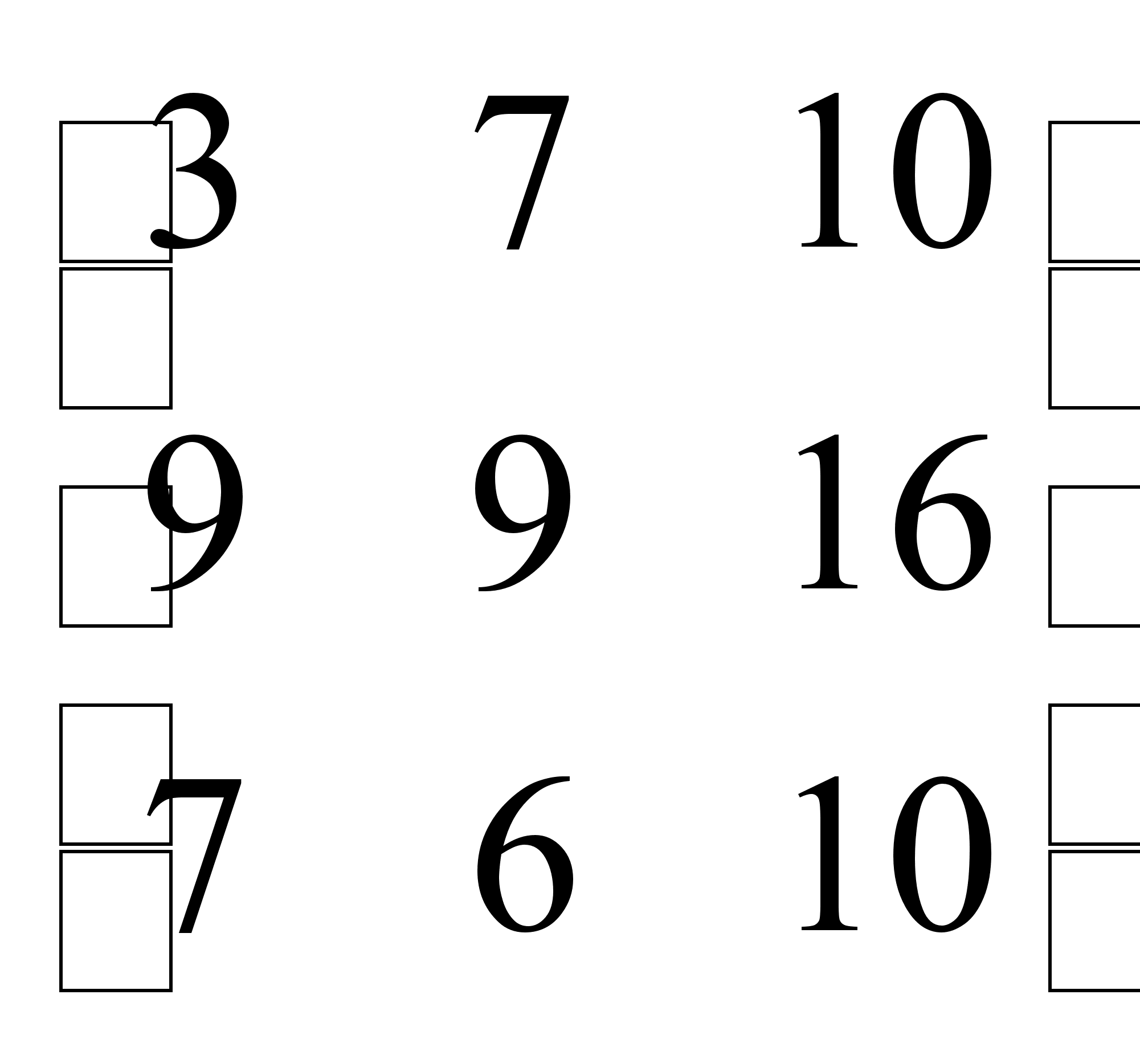 .
. пределение.Эллипсом называется линия, заданная уравнением
пределение.Эллипсом называется линия, заданная уравнением 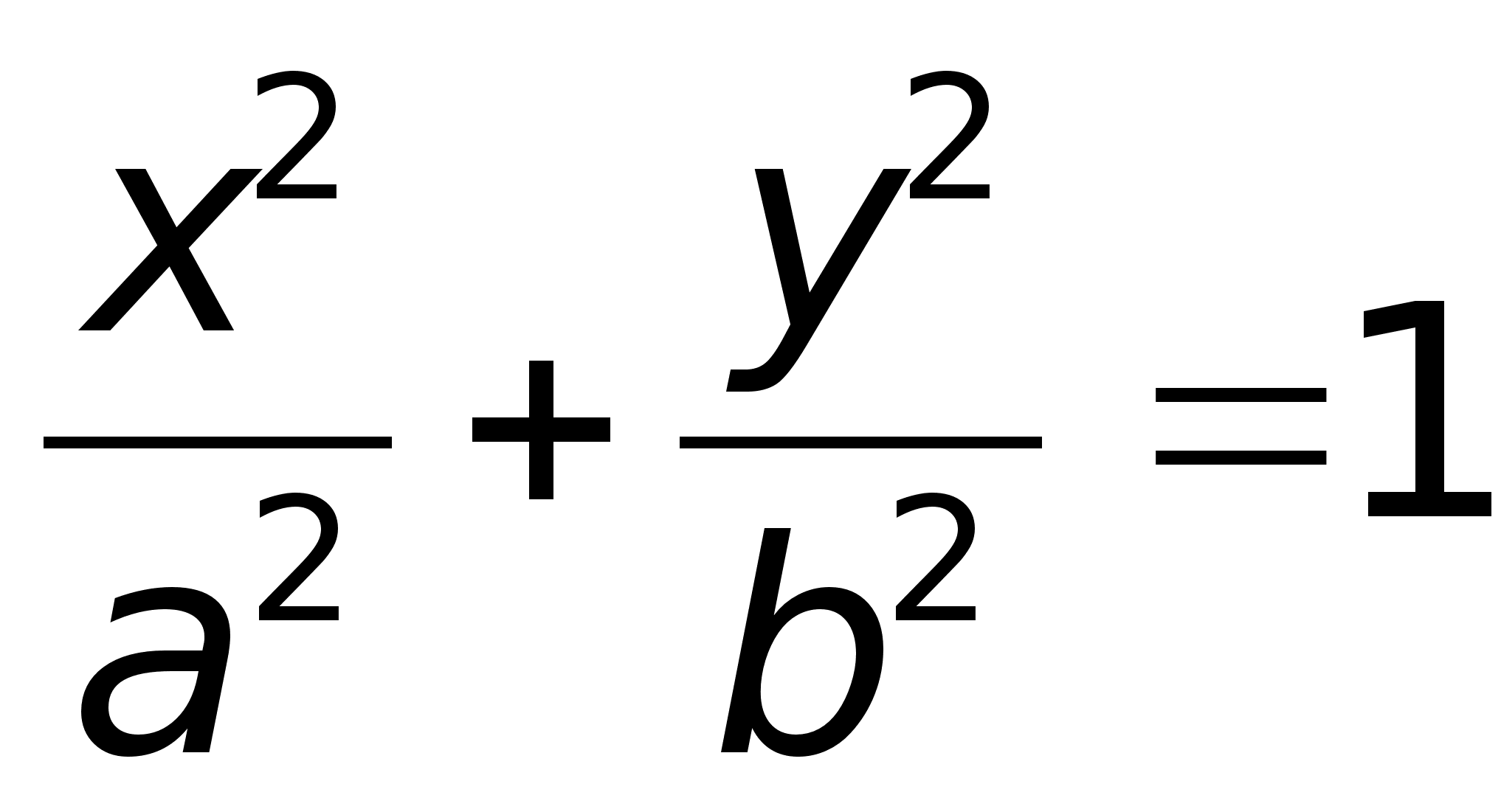 .Определение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.
.Определение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.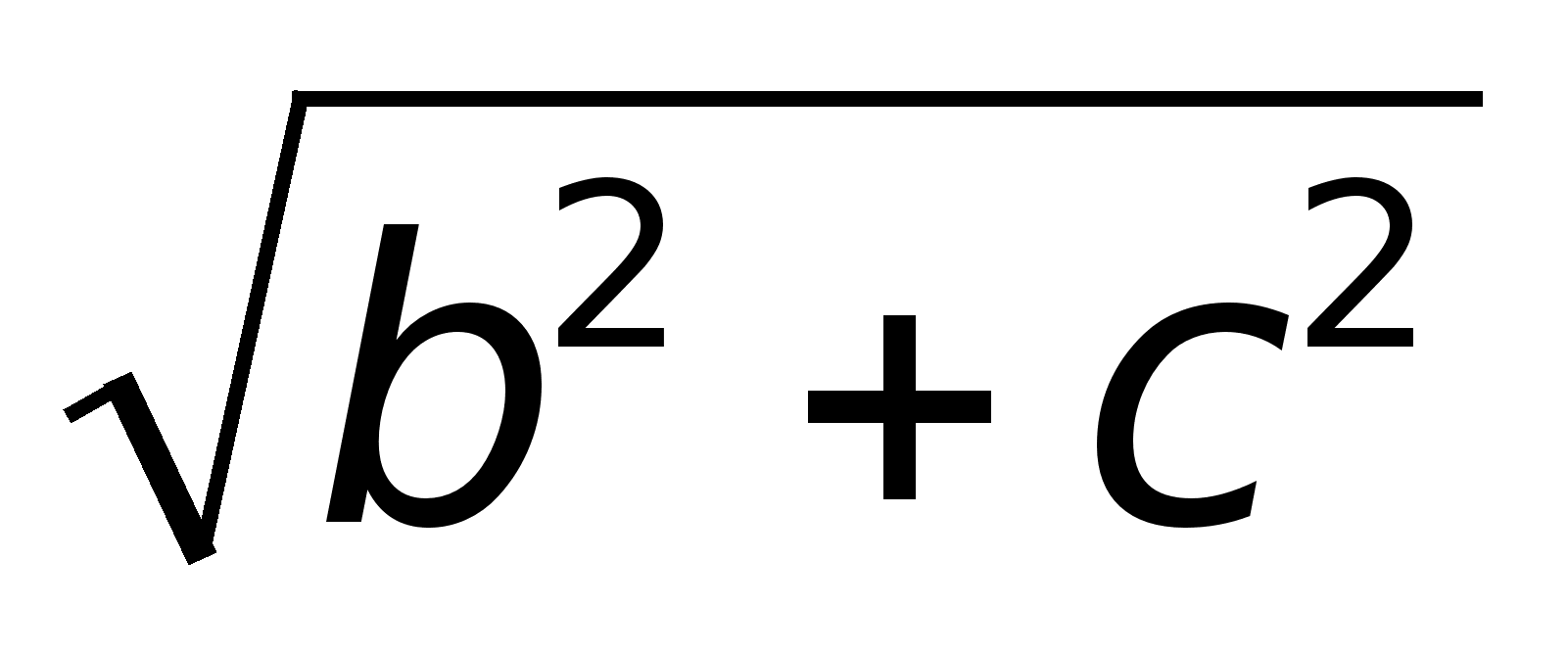 (по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r1 + r2 = a – c + a + c. Т.к. по определению сумма r1 + r2 – постоянная величина, то , приравнивая, получаем:a2 = 2 + c2 r1 + r2 = 2a. Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.Е = с/a. Т.к. с Определение. Величина k = b/a называется коэффициентом сжатия эллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса.Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – e2.Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.Если для точки М(х1, у1) выполняется условие:
(по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r1 + r2 = a – c + a + c. Т.к. по определению сумма r1 + r2 – постоянная величина, то , приравнивая, получаем:a2 = 2 + c2 r1 + r2 = 2a. Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.Е = с/a. Т.к. с Определение. Величина k = b/a называется коэффициентом сжатия эллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса.Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – e2.Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.Если для точки М(х1, у1) выполняется условие: 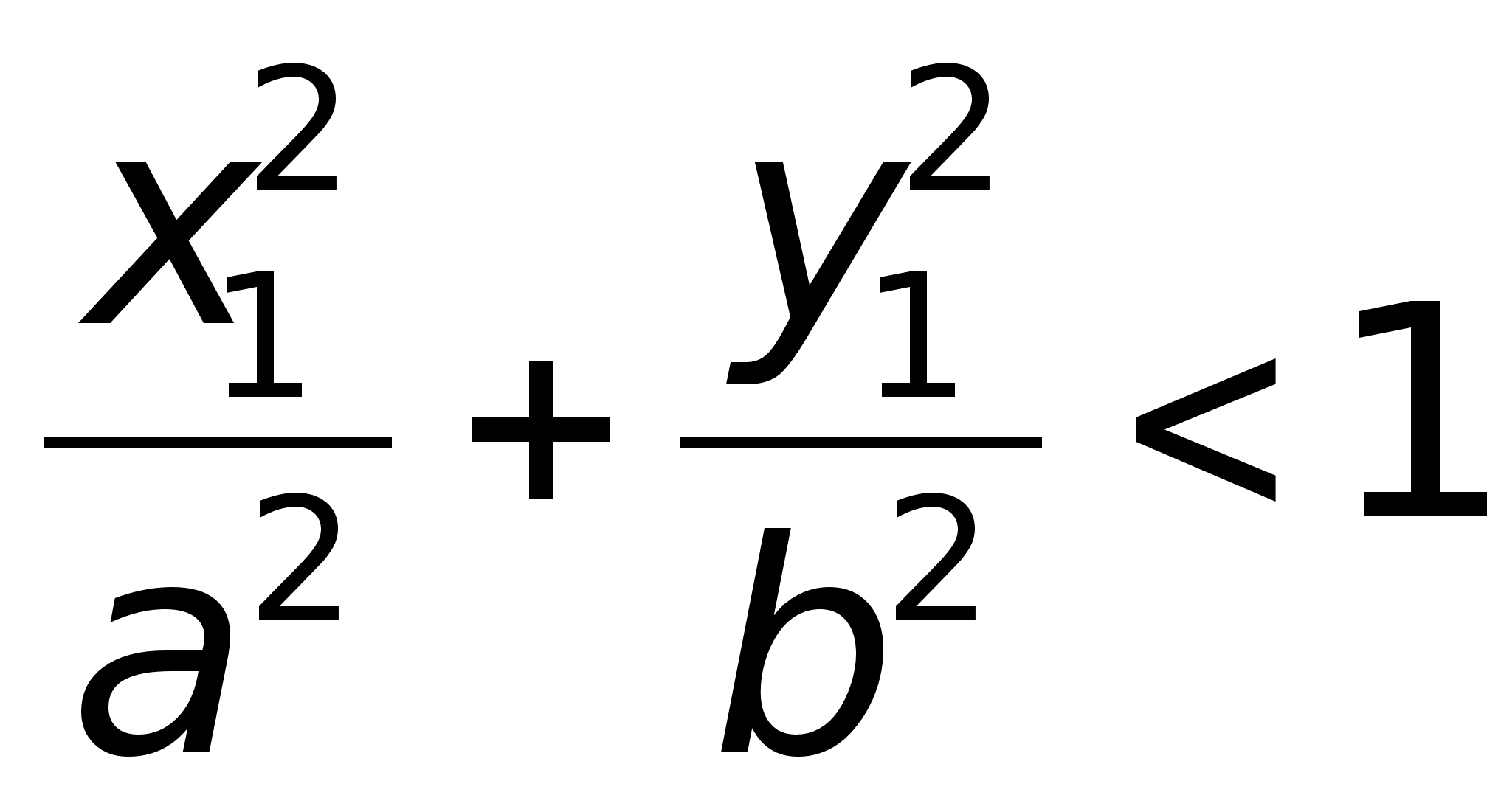 , то она находится внутри эллипса, а если
, то она находится внутри эллипса, а если 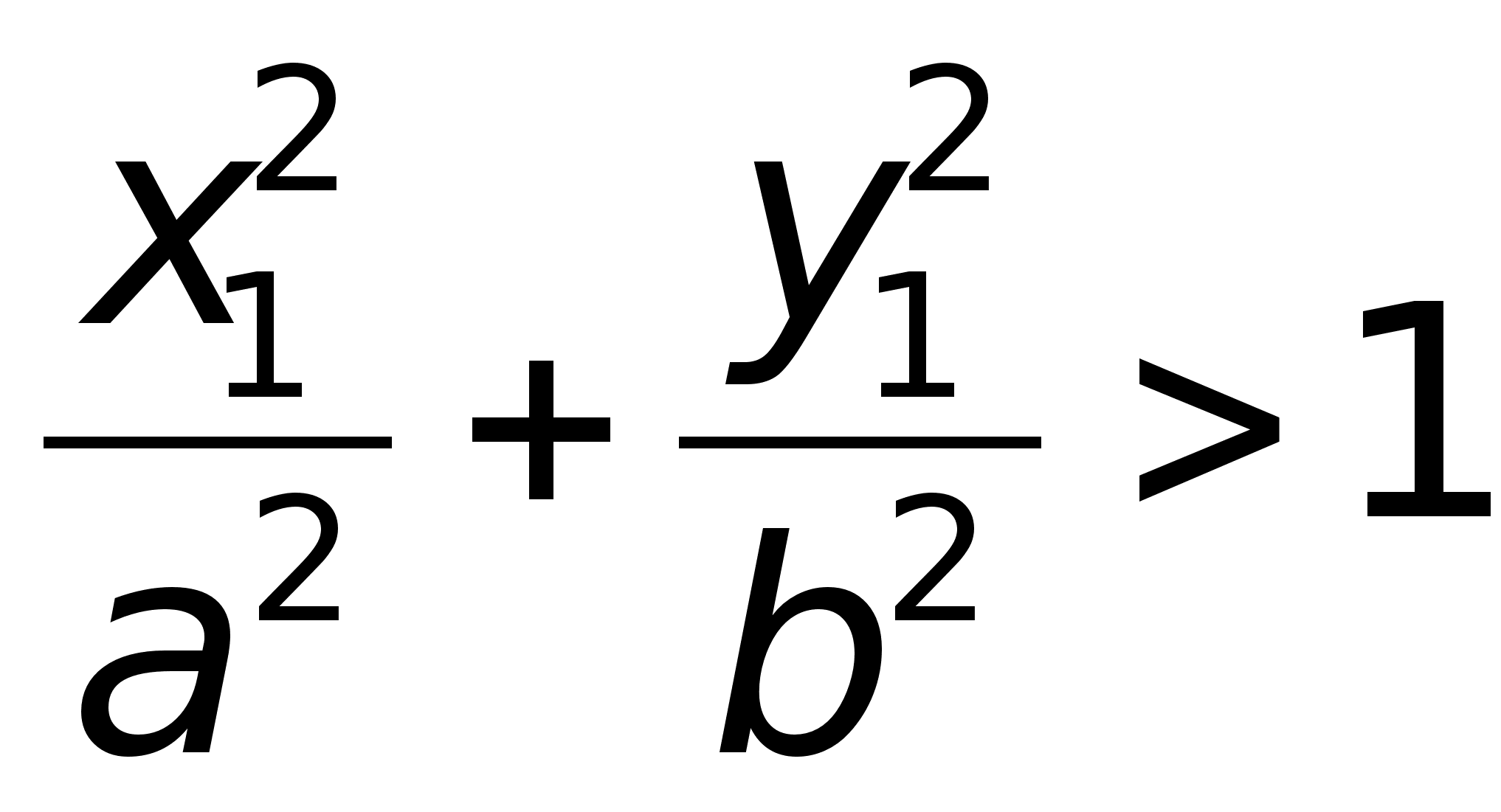 , то точка находится вне эллипса.Теорема.Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:r1 = a – ex, r2 = a + ex. Доказательство. Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать:
, то точка находится вне эллипса.Теорема.Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:r1 = a – ex, r2 = a + ex. Доказательство. Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать: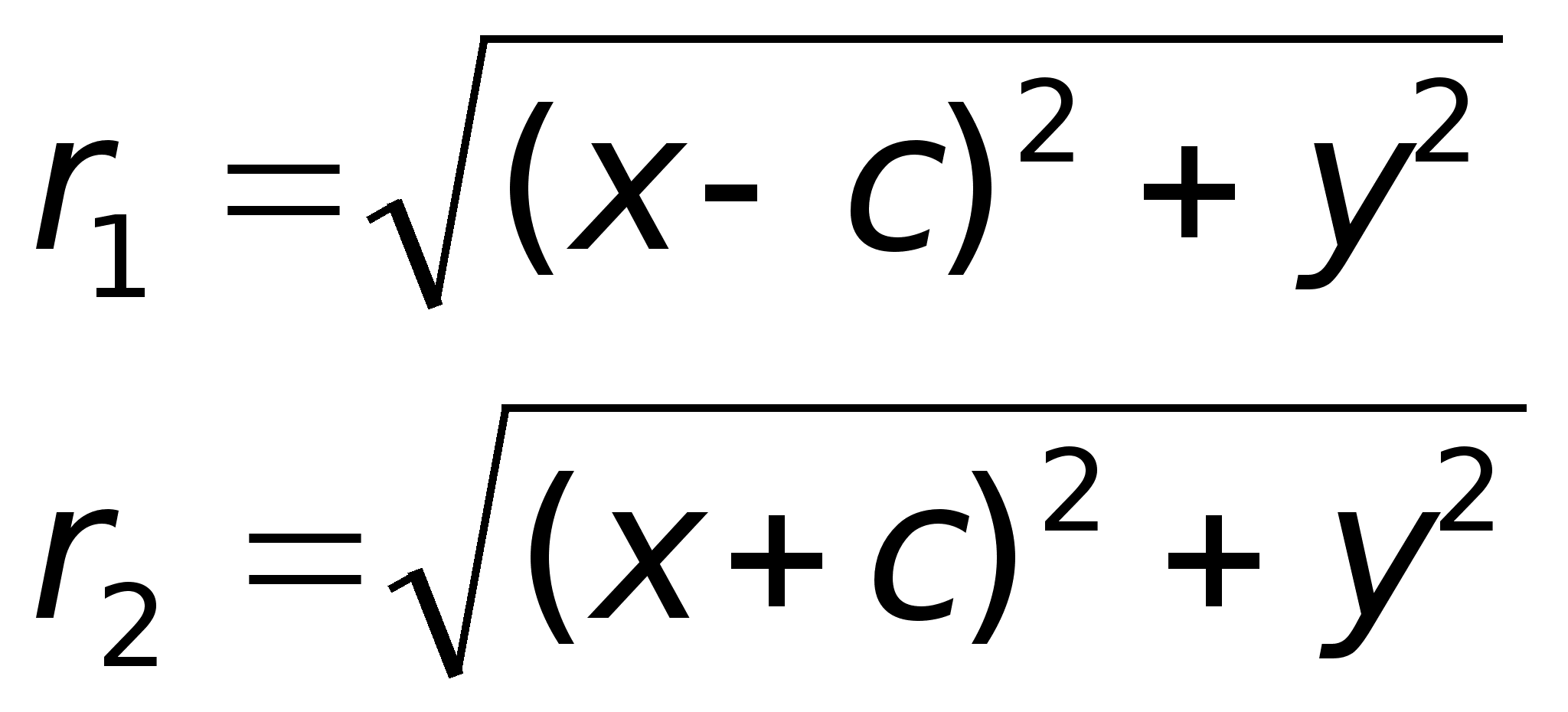
 После возведения в квадрат и приведения подобных слагаемых:
После возведения в квадрат и приведения подобных слагаемых: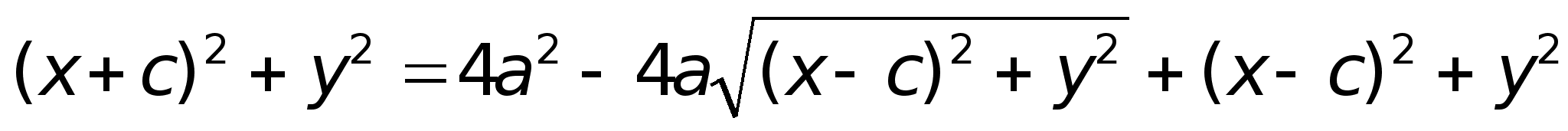

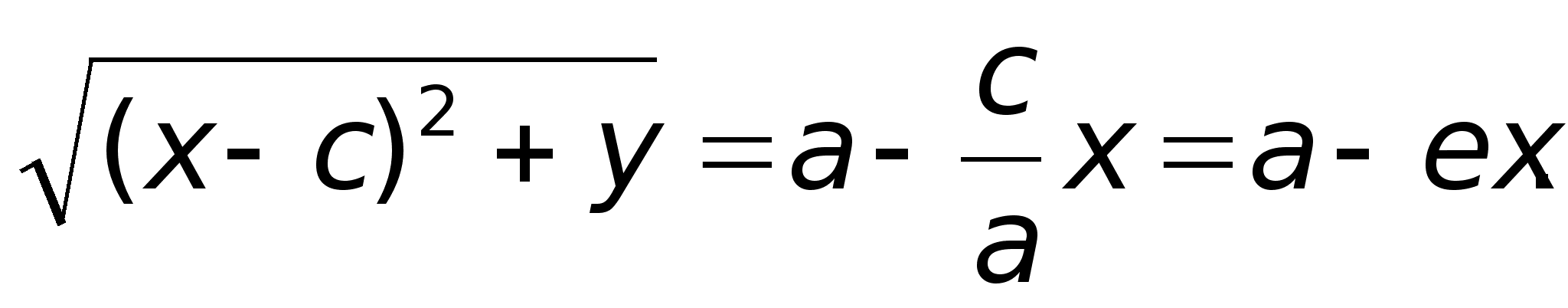 Аналогично доказывается, что r2 = a + ex. Теорема доказана.С эллипсом связаны две прямые, называемые директрисами. Их уравнения: x = a/e; x = -a/e.Теорема.Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением:
Аналогично доказывается, что r2 = a + ex. Теорема доказана.С эллипсом связаны две прямые, называемые директрисами. Их уравнения: x = a/e; x = -a/e.Теорема.Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением: 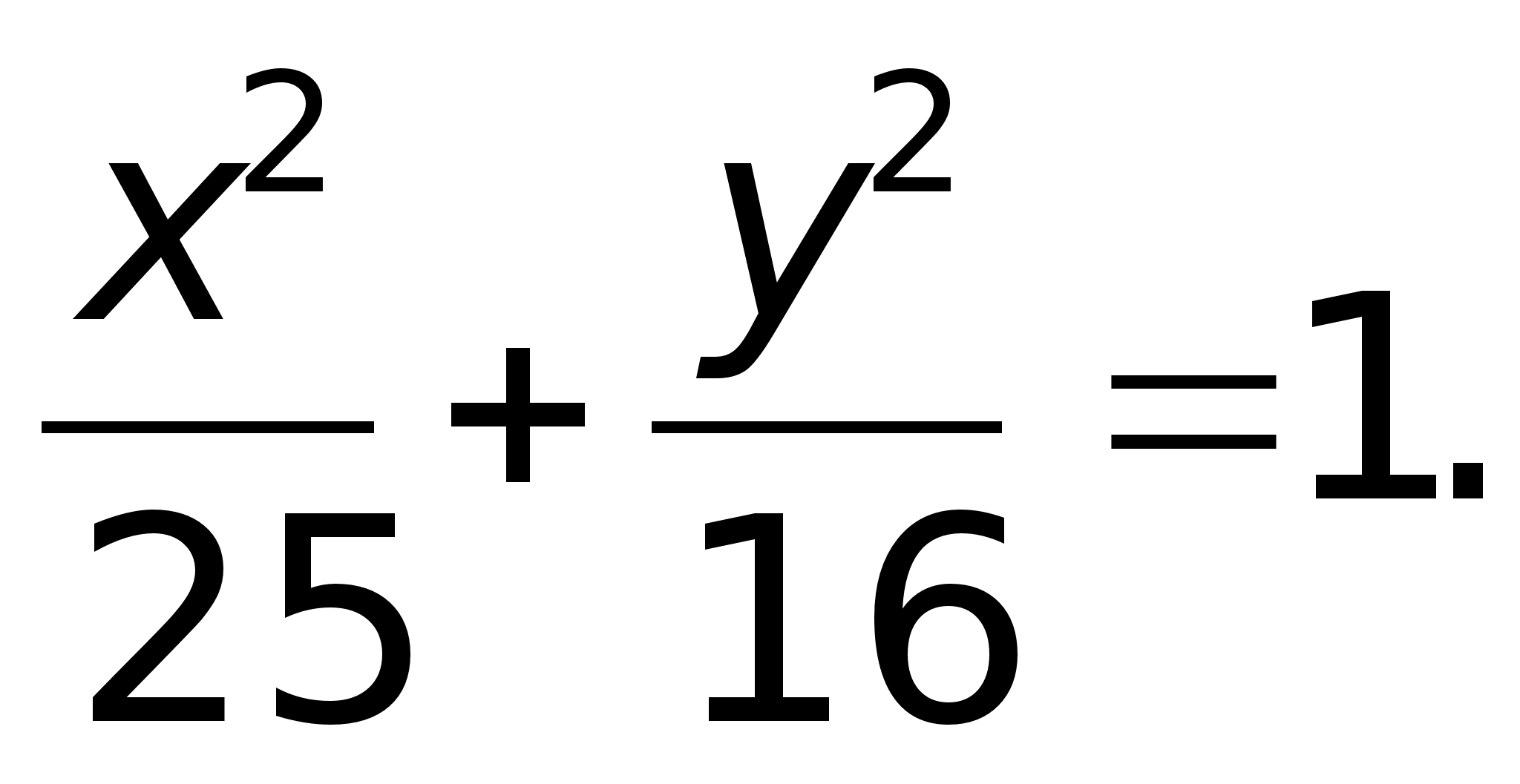 Координаты нижней вершины: x = 0; y2 = 16; y = -4. Координаты левого фокуса: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0). Уравнение прямой, проходящей через две точки:
Координаты нижней вершины: x = 0; y2 = 16; y = -4. Координаты левого фокуса: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0). Уравнение прямой, проходящей через две точки:  Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.Уравнение эллипса имеет вид:
Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.Уравнение эллипса имеет вид:  , таким образом, a2 – b2 = c2 = Ѕпо условию 2а = 2, следовательно а = 1, b =
, таким образом, a2 – b2 = c2 = Ѕпо условию 2а = 2, следовательно а = 1, b =  Итого:
Итого:  .
.
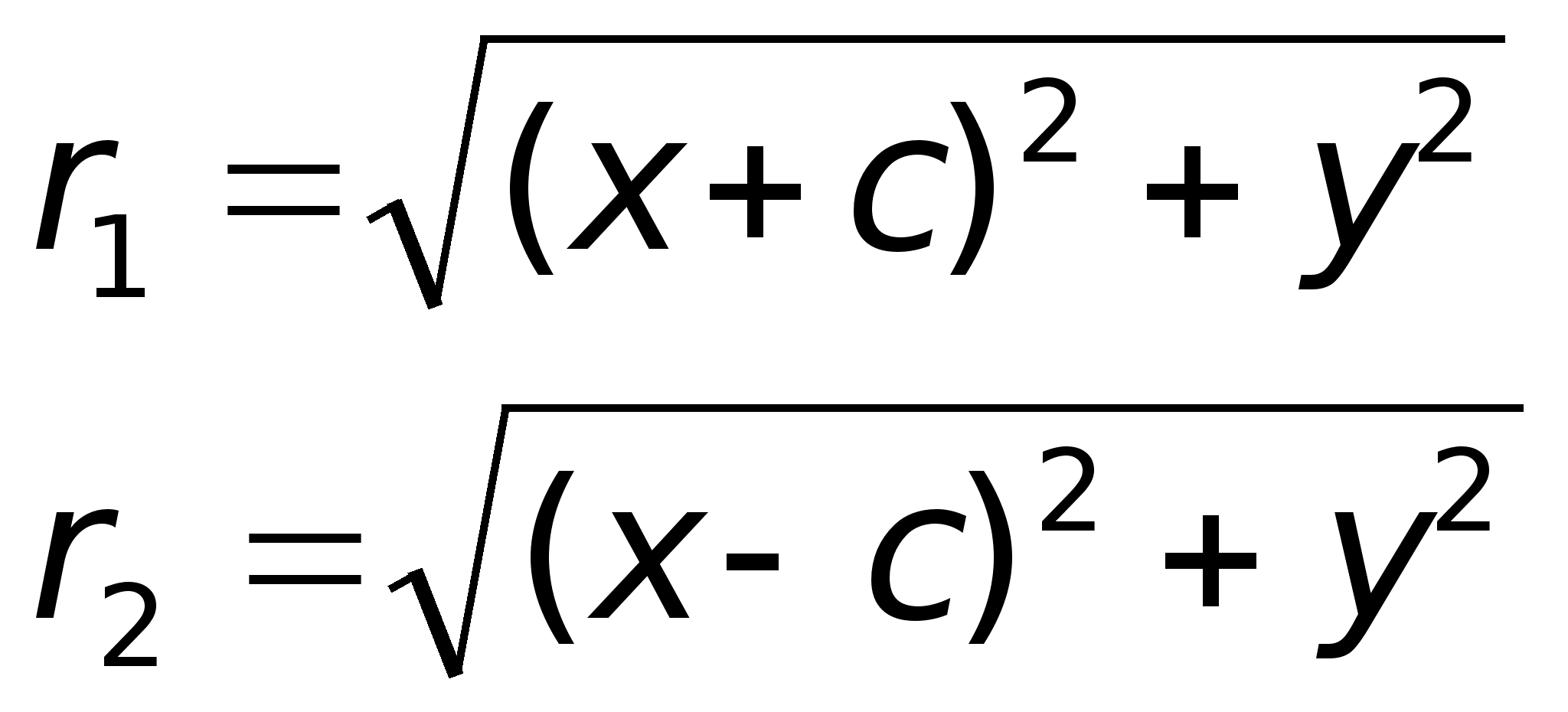

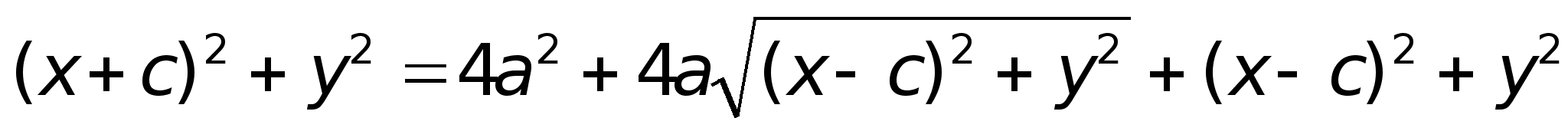
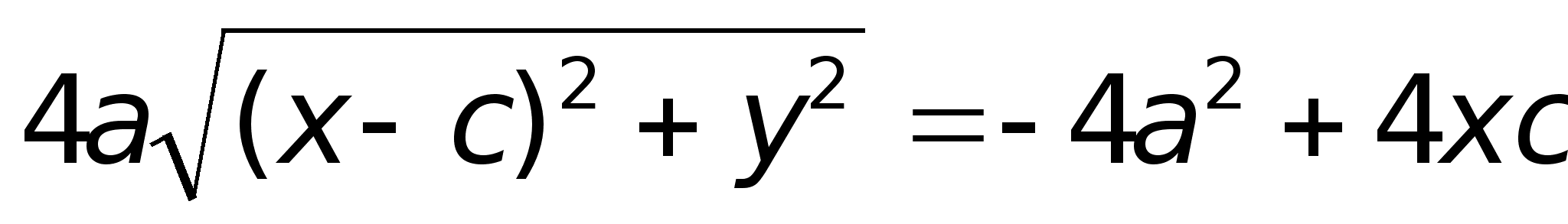
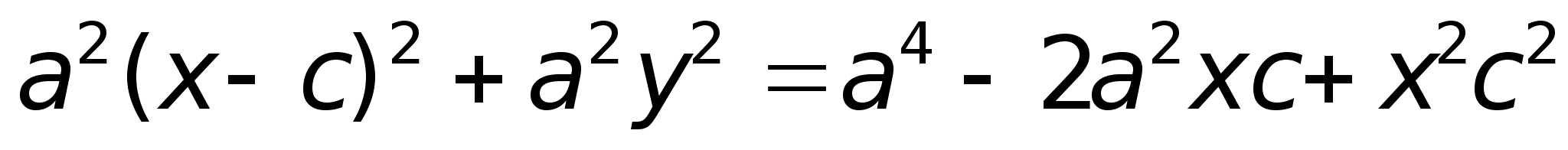
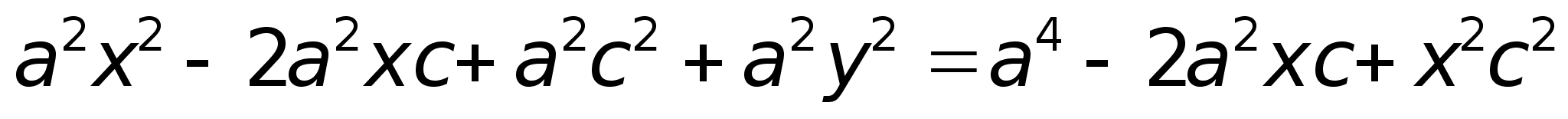
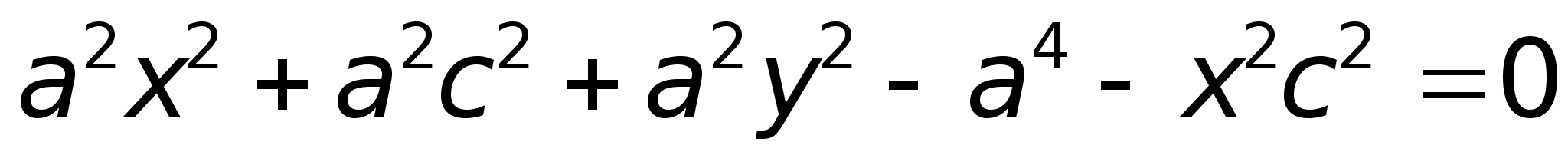

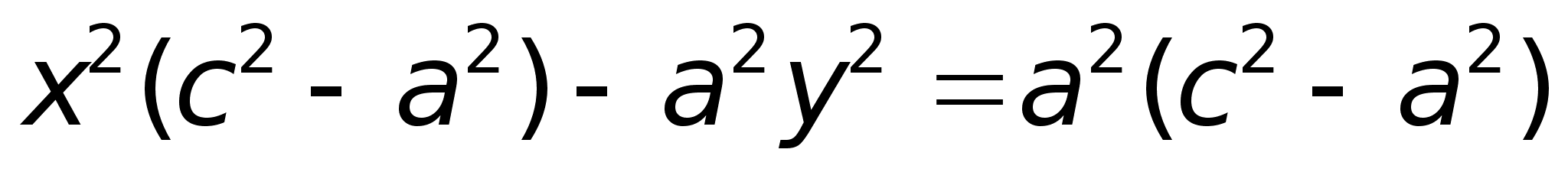
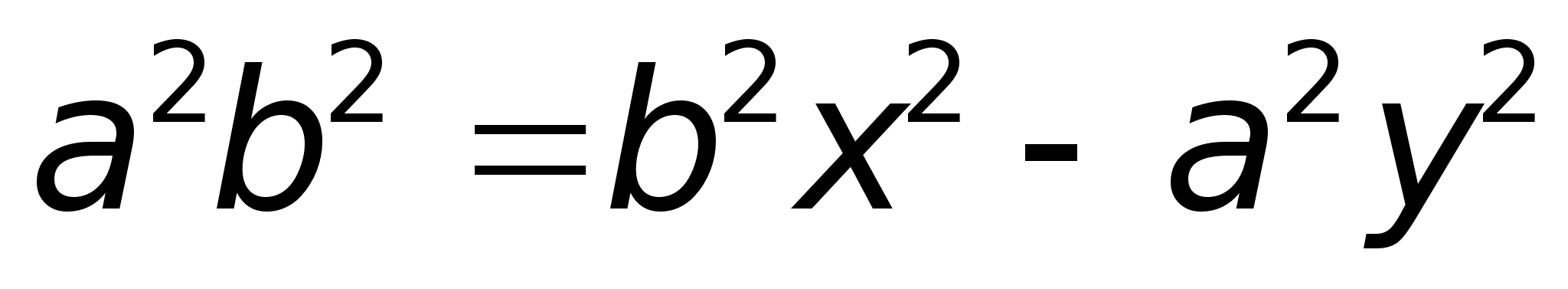
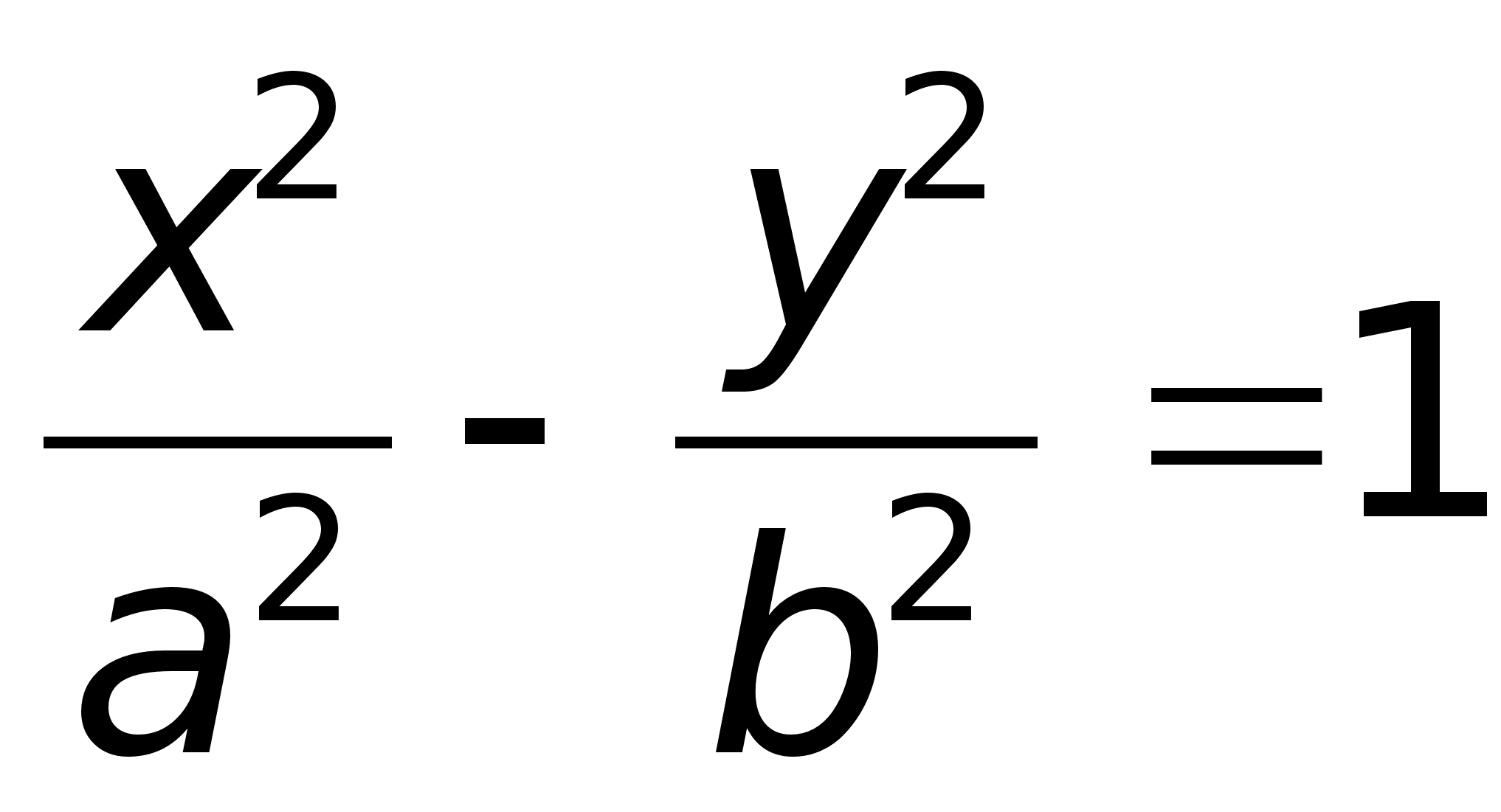 Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.Ось 2а называется действительной осью гиперболы.Ось 2b называется мнимой осью гиперболы.Гипербола имеет две асимптоты, уравнения которых
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.Ось 2а называется действительной осью гиперболы.Ось 2b называется мнимой осью гиперболы.Гипербола имеет две асимптоты, уравнения которых  Определение. Отношение
Определение. Отношение  называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.С учетом того, что с2 – а2 = b2:
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.С учетом того, что с2 – а2 = b2: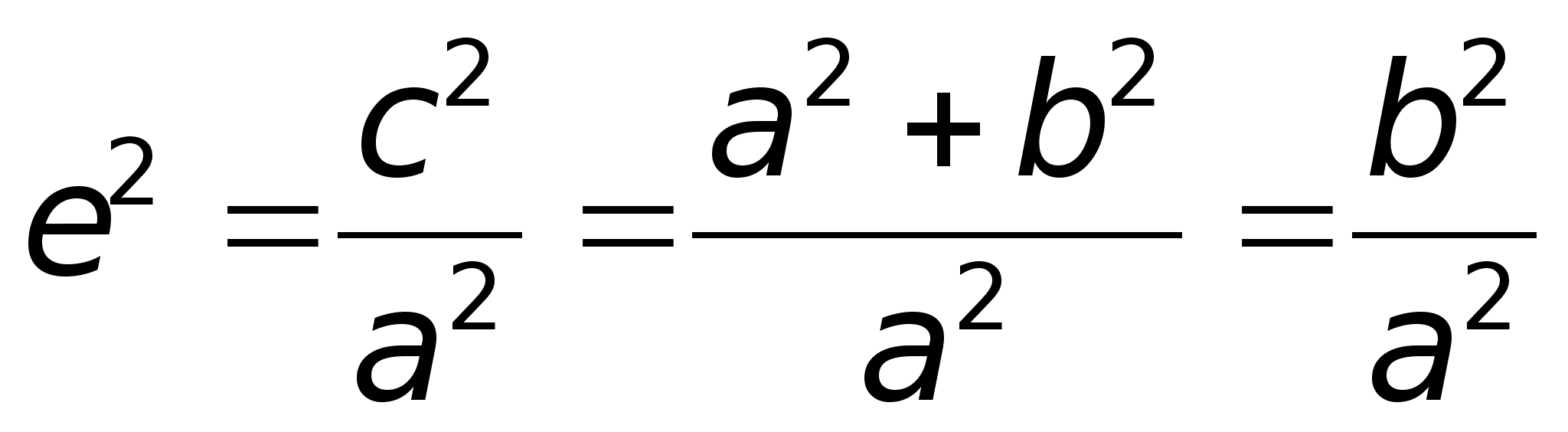
 Если а = b, e =
Если а = b, e =  , то гипербола называется равнобочной (равносторонней).Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения:
, то гипербола называется равнобочной (равносторонней).Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: 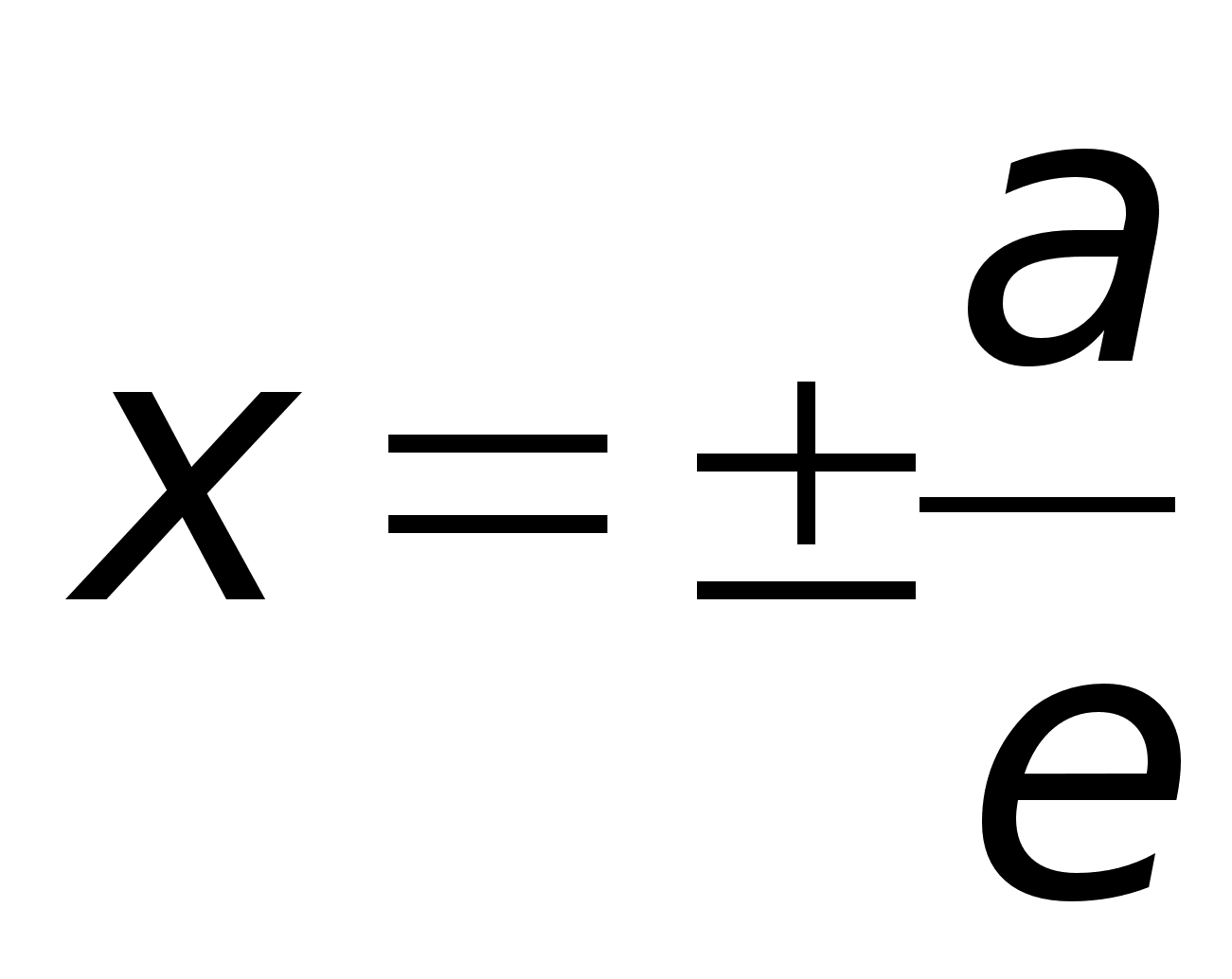 .Теорема.Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
.Теорема.Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.


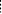


 - Каноническое ур-е эллипса
- Каноническое ур-е эллипса
 пределение.Комплексным числом zназывается выражение
пределение.Комплексным числом zназывается выражение  , где aи – действительные числа, i – мнимая единица, которая определяется соотношением:
, где aи – действительные числа, i – мнимая единица, которая определяется соотношением: При этом число a называется действительной частью числа z (a = Rez), а - мнимой частью ( = Imz).Если a =Rez =0, то число z будет чисто мнимым, если = Imz = 0, то число z будет действительным.Определение. Числа
При этом число a называется действительной частью числа z (a = Rez), а - мнимой частью ( = Imz).Если a =Rez =0, то число z будет чисто мнимым, если = Imz = 0, то число z будет действительным.Определение. Числа  называются комплексно – сопряженными. Определение. Два комплексных числа
называются комплексно – сопряженными. Определение. Два комплексных числа 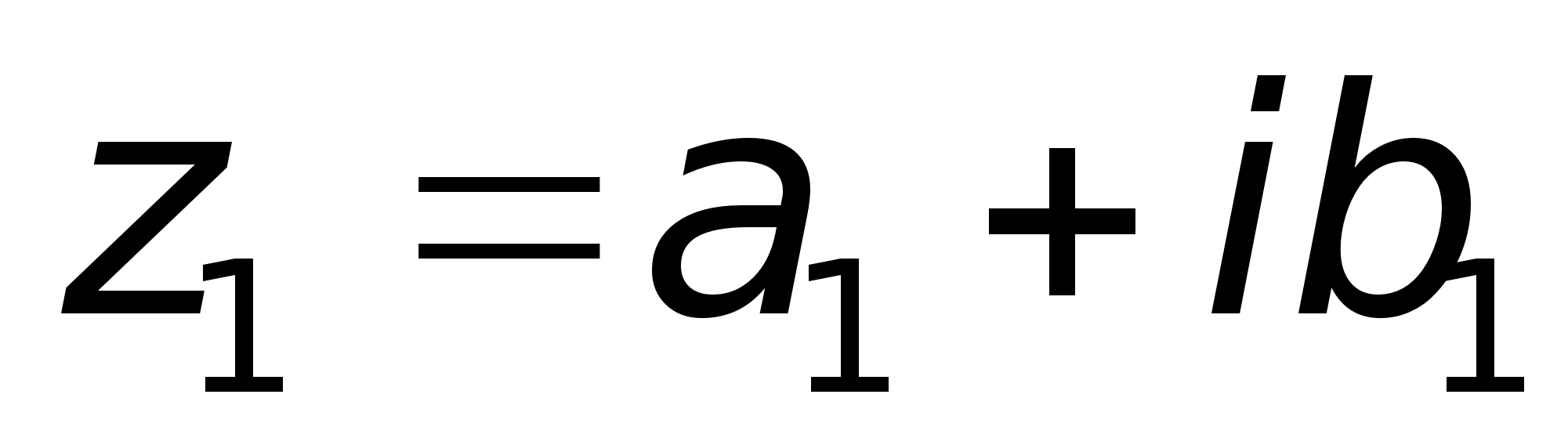 и
и  называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части: Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.
Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части. Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью. A(a,b)
Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью. A(a,b) 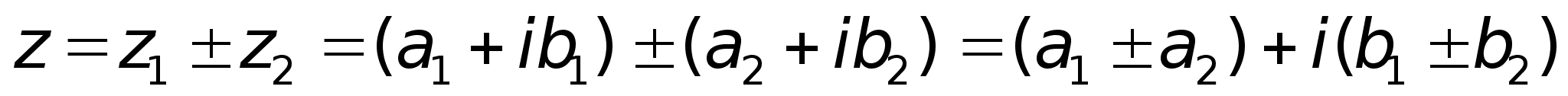 ;
;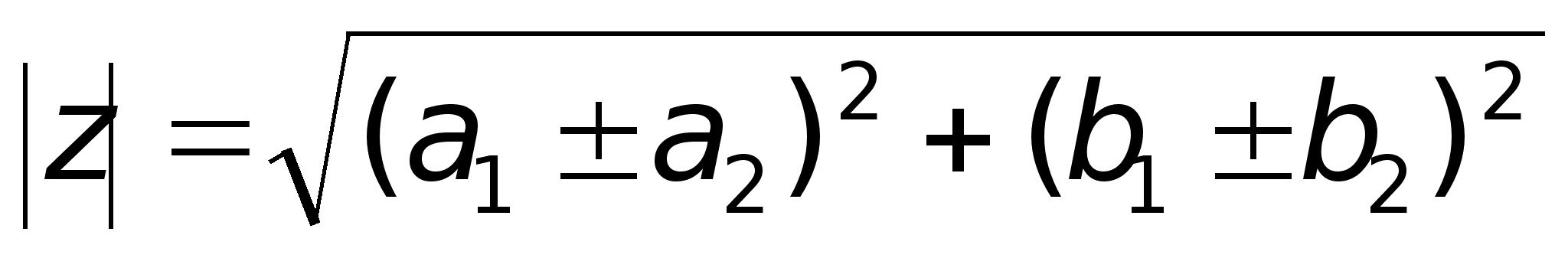 ;2) Умножение.
;2) Умножение.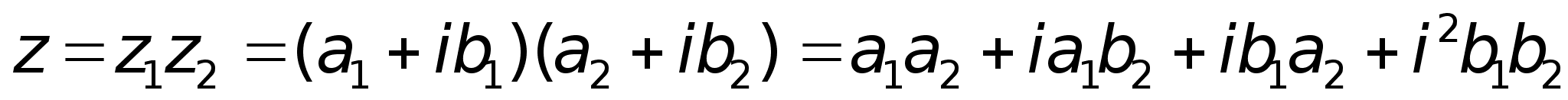
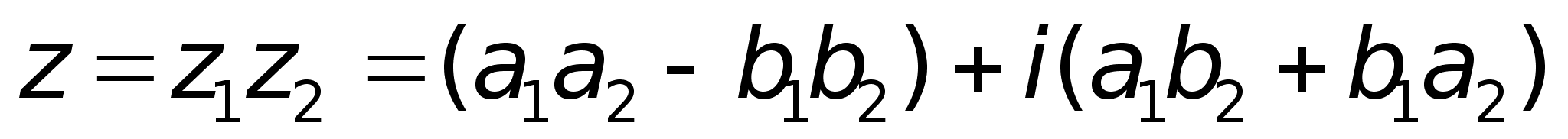 В т
В т