Экономико-математические модели задач о смесях на примере СПК "Родина"
Успешность решения подавляющего большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. И от того, как будут распределяться эти, как правило, ограниченные ресурсы, зависит конечный результат деятельности, бизнеса.
Суть методов оптимизации заключается в том, что исходя из наличия определенных ресурсов выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя.
При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации.
Отличительными признаками оптимизационных моделей являются:
- наличие одного или нескольких критериев оптимальности (критерий оптимальности - это признак, по которому множество или одно решение задачи признается наилучшим); наиболее типичными критериями в экономических оптимизационных задачах являются: максимум дохода или прибыли, минимум издержек, минимальное время для выполнения задания и другие;
- система ограничений, которая формируется, исходя из содержательной постановки задачи, и представляет собой систему уравнений или неравенств.
В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования): линейное, нелинейное и динамическое.
Линейное программирование (планирование) - математический метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изображаются в виде прямых линий, обозначающих 1-е степени соответствующих величин.)
Максимизируемая (минимизируемая) функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели. Она носит название целевой функции.
Ограничения характеризуют имеющиеся возможности решения задачи.
Существо решения задач линейного программирования заключается в нахождении условий, обращающих целевую функцию в минимум или максимум.(7. c.13)
Решение, удовлетворяющее условиям задачи и соответствующее намеченной цели, называется оптимальным планом.
Линейное программирование (планирование) служит для выбора наилучшего плана распределения ограниченных однородных ресурсов в целях решения поставленной задачи.
Этапы построения оптимизационных экономико-математических моделей.
1) Выбор объекта исследования. Ими могут быть различные производственно-экономические процессы: раскрой промышленного материала, загрузка производственных мощностей, перевозка грузов, размещение производства и т.д.
2) Определение цели исследования. Ее формулируют на основе задач, поставленных при изучении данного объекта.
3) Выбор критерия оптимальности. Отличительной особенностью оптимизационных моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функций.
Критериями оптимальности обычно служат: минимальная стоимость, максимальный доход, минимальные издержки и т.д. Неправильно выбранный критерий оптимальности может привести к решению, не отвечающему цели поставленной задачи.
4) Выявление основных ограничений. При построении моделей необходимо найти основные ограничения и включить их в модель. Реальная задача обычно содержит большое число ограничений, часть из которых вытекает из условия задачи, другие можно выявить лишь после решения, которое по каким-либо требованиям не устраивает.
Целью данной курсовой работы является изучениематематических моделей оптимального планирования производства на сельскохозяйственном предприятии, а также возможности их применения на реальном объекте хозяйственной деятельности.
Тема, рассматриваемая в данной курсовой работе, довольно широко освещена в литературе. При написании работы использовались, например, работы таких авторов, как: Гасс С.И., Вагин Е.А., Попов И.П., Барсов А.С. и других.
Данная курсовая работа состоит из введения, трех глав, списка использованной литературы и приложений. В первой главе описаны общая классификация экономико-математических моделей, принципы построения и структура интегрированной системы экономико-математических моделей.
Вторая глава состоит из двух подразделов, в которых описываются основные типы линейных экономико-математических моделей и методы решения задач о смесях.В третьей главе – организационно-экономическая характеристика и технико-экономические показатели работы СПК «Родина», постановка и решение задачи о смесях на примереСПК «Родина».
Решение задачи о рационе производилось при помощи ресурса Поиск решения MS Excel ввиду сложности построенной экономико-математической модели. Описание методики вычисления с помощью данного инструмента приведено в третьей главе.
Глава 1. Теоретические основы экономико-математических задач о смесях
1.1 Общая классификация экономико-математических моделей
Экономико-математические модели подразделяются на: статистические, балансовые и оптимизационные.
Статистические модели – это модели, в которых описываются корреляционно-регрессионые зависимости результата производства от одного или нескольких независимых факторов. Эти модели широко используются для построения производственных функций, а также при анализе экономических систем.
Балансовые модели представляют систему балансов производства и распределения продукции и записываются в форме шахматных квадратных матриц. Балансовые модели служат для установления пропорций и взаимосвязей при планировании различных отраслей народного хозяйства.
Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания наилучших (оптимальных) решений конкретной экономической задачи. Эти модели, в отличие от статистических и балансовых, относятся к классу экстремальных задач и описывают условия функционирования экономической системы.
Классификация экономико-математических моделей может быть различной и условной. Это зависит от того, на базе каких признаков строится модель. В основу классификации кладутся различные признаки. Так, по функциональному признаку модели подразделены на модели планирования, модели бухгалтерского учета, модели экономического анализа, модели информационных процессов.
По признаку размерности модели классифицируются на макромодели, локальные модели и микромодели. Макроэкономические модели строятся для изучения народного хозяйства республики в целом на базе укрупненных показателей. Цель таких моделей состоит в разработке более обоснованных перспективных планов народнохозяйственного развития на основе познания важнейших экономических пропорций и соотношений, темпов роста производства и уровней потребления, рациональной отраслевой структуры.
Макромодели в зависимости от принятых уровней детализации подразделяются на: односекторные, двухсекторные и многосекторные. В двухсекторной модели выделяется группа производства средств производства и группа производства предметов потребления. Однако двухсекторные модели в силу весовой агрегированности показателей не позволяют непосредственно решать задачи, которые возникают в процессе планирования.
Более полная информация о механизме взаимосвязей в народном хозяйстве представляется многосекторными моделями, в которых сфера материального производства представляется состоящей из десятков, а порой и сотен самостоятельных отраслей
В основе всех экономических макромоделей лежит уравнение баланса
X - F(Х) - W = Z,
где X - совокупный общественный продукт;
F(Х) - производственная функция (прямые затраты), показывающая долю совокупного общественного продукта, необходимую для его производства;
W - доля совокупного общественного продукта, идущая на потребление;
Z - доля совокупного общественного продукта, идущая на накопление.
Макромодели могут разрабатываться и для отдельных отраслей народного хозяйства, например, тракторостроения, машиностроения на ближайшую перспективу.
К локальным экономическим моделям можно отнести также модели, с помощью которых анализируются и прогнозируются некоторые показатели развития отрасли. Например, модель прогноза научно-технического прогресса, модель прогноза производительности труда и т. д.
Микромодели на предприятиях разрабатываются для углубленного анализа структуры производства. Они позволяют выявить резервы роста объемов производства продукции. При построении микромоделей широко используются методы математической статистики — корреляционный и регрессионный, индексный и выборочный методы.
Оптимизационные модели могут носить детерминированный и стохастический характер. В детерминированных моделях результат решения однозначно зависит от входных данных. В стохастических вероятностных моделях - определенный набор входных данных может дать, а может и не дать соответствующего результата. Стохастические модели описывают случайные процессы, в которых результат всегда остается неопределенным в отличие от детерминированных моделей, входная информация которых заранее предопределяет результат решения.
Наиболее разработаны и практически более применимы детерминированные модели, использующие аппарат математического программирования.
Поскольку экономико-математическая модель отражает объективные закономерности воспроизводства определенного объекта или отдельные стороны этого процесса с помощью различных математических средств, то любая модель характеризуется рядом признаков, часть которых относится к отражаемым свойствам моделируемого объекта (процесса), а часть связана с самим аппаратом моделирования.
В основу классификации положен следующий прием: выделены четыре признака объекта и три признака по средствам построения моделей.
Моделируемые объекты рассматриваются с позиций:
1) сущности моделируемых процессов воспроизводства;
2) временных характеристик процессов;
3) уровней управления процессами (объектами);
4) назначения моделей в управлении.
В основу классификации по средствам их построения положены:
1) средства моделирования и методы реализации моделей;
2) структура моделей и характер зависимости ее компонентов;
3) используемая информация.
Каждая из этих совокупностей классификационных процессов отражает математическую и информационную сторону моделей. Приведенная классификация моделей условна. Она проводится по вполне определенным общим признакам моделей.
Классификация моделей, их анализ являются предпосылкой для построения интегрированной системы моделей.
1.2 Принципы построения и структура интегрированной системы экономико-математических моделей
Динамичность развития общественного производства и повышения его эффективности требуют совершенствования методов управления. Одним из важнейших направлений современного состояния производства во всех отраслях народного хозяйства является разработка методологии интегрированной системы экономико-математических моделей.
Сущность интегрированной системы состоит в изучении объекта как сложной динамической системы, состоящей из множества функционирующих во взаимодействии элементов. При этом изменения, происходящие хотя бы с одним элементом, отражаются на эффективности в целом всей системы.
Интегрированная система экономико-математических моделей представляет совокупность логически, информационно и алгоритмически связанных моделей, отражающих экономические, организационные и технологические процессы воспроизводства в их объективно существующем единстве. Только во взаимосвязи всех моделей системы обеспечивается комплексное решение задач управления производством. В систему включаются различные модели, отражающие воспроизводство экономического объекта. Это модели по функционирующим показателям эффективности производства, таким, как производительность труда, себестоимость единицы продукции, валовая продукция, прибыль, рентабельность, объем капитальных вложений и другие показатели. К интегрированной системе можно отнести модели ценообразования, модели финансирования и кредитования, налогообложения.
Использование интегрированной системы моделей в управлении производством возможно только на основе широкого применения экономико-математических методов и ЭВМ.
Интегрированная система моделей строится с учетом общих методологических принципов. Это принципы развития, единства, относительной автономности, соответствия и адаптации.
Принцип развития требует постоянного совершенствования системы моделей, включения в ее состав новых моделей, использование которых становится необходимым и возможным по мере общего совершенствования методологии планирования и управления. Развитие системы моделей требует соответствующего развития информационного и математического обеспечения плановых и прогнозных расчетов.
Принцип единства означает представление всего комплекса экономико-математических моделей в единой структуре взаимосвязанных блоков. Существенным требованием является общность методологического подхода к построению однотипных моделей, используемых на разных уровнях управления производством. Важнейшим условием выступает единство математического обеспечения системы.
Принцип относительной автономности предусматривает возможность выделения из общей системы моделей относительно самостоятельных частей, которые можно разрабатывать и внедрять, не ожидая полного завершения работ по всей системе моделей. Этот принцип позволяет разрабатывать локальные системы плановых расчетов по конкретным показателям.
Принципы соответствия и адаптации в системе экономико-математических моделей означают соответствие системы моделей сложившимся уровням управления. Модели для каждого уровня отличаются степенью детализации отражаемых процессов. В зависимости от уровня управления выделяют следующие комплексы моделей:
1) регионального (республиканского, областного, районного);
2) предприятий и их подразделений.
Учитывая совершенствование организационной структуры управления и методологии планирования, изменения структуры плановых документов, необходимо, чтобы система моделей адаптировалась к изменяющимся условиям, что означает реализацию принципа соответствия.
Кроме рассмотренных общеметодологических принципов, выделяют ряд специфических принципов, имеющих важное значение для построения интегрированной системы моделей. Это такие принципы, как принцип ориентации на выходные плановые показатели, принцип необходимого разнообразия, принцип взаимного дополнения групп моделей, принцип увязки моделей.
Принцип ориентации на выходные плановые показатели означает, что система моделей и решение с ее помощью плановых задач должна обеспечить выход на утверждаемые и контролируемые плановые показатели. Это условие влияет на степень детализации моделей, на разрабатываемые алгоритмы и программы расчетов и в значительной мере на состав входной информации.
Принцип необходимого разнообразия состоит в том, что для адекватного отражения объективных процессов в состав системы моделей следует включать разнообразные модели, в том числе реализующие методы математической статистики и математического программирования, межотраслевого баланса, сетевые и имитационные модели. Выбор математического аппарата .для построения и реализации моделей должен определяться особенностью моделируемого процесса и возможностями программного и технического обеспечения расчетов.
Принцип взаимного дополнения групп моделей заключается в том, что для каждого из основных блоков системы моделей целесообразно выделять три взаимодополняющие группы моделей, имеющие специфическое направление. Модели первой группы предназначены для прогнозирования состояния ресурсов и ряда отправных показателей планирования. Модели этой подготовительной группы предназначены для обеспечения входной информацией расчета основных показателей плана. Вторая основная группа моделей включает модели для проведения основных оптимизационных и балансовых расчетов, для увязки плановых показателей производства, материально-технического обеспечения, финансирования. Модели этой группы обеспечивают выход на основные утверждаемые и контролируемые плановые показатели. И, наконец, модели третьей, заключительной, группы предназначены для дополнительных расчетов, например, для более детального представления ряда натуральных и стоимостных балансов, планов распределения ресурсов в объекте и других вспомогательных расчетов.
Принцип увязки моделей означает, что между моделями групп и блоками системы в целом должны устанавливаться три вида связей: логическая, информационная и алгоритмическая.
Логическая связь определяет общую последовательность реализации моделей в системе, логику взаимного согласования разнообразных моделей.
Информационная связь строится на базе того, что результативная информация этих моделей служит входной информацией для других. Информационная связь между моделями характеризуется горизонтальной и вертикальной связями. Горизонтальная - связывает модели для планирования в одном объекте. При этом поток информации от моделей долгосрочного планирования к моделям средне- и краткосрочного планирования называют ориентирующим потоком. Вертикальные связи между моделями служат отражением реальных связей в планировании производства между различными уровнями управления.
Алгоритмическая связь - совокупность алгоритмов и программ для преобразования входной и выходной информации по всей системе моделей.
Глава 2.Методы решения экономико-математических задач о смесях
2.1 Основные типы линейных экономико-математических моделей
Среди линейных моделей математического программирования особое место занимают четыре типа моделей:
1) модель общей задачи линейного программирования- применяют для решения задач на смеси, использования сырья, определение оптимального плана выпуска изделий и ряда других. В каждой из них отыскивается оптимум целевой функции
![]()
при линейных ограничениях
![]()
![]() ;
;
2) модель транспортной задачи линейного программирования- состоит в том, чтобы наивыгоднейшем образом прикрепить поставщиков однородного продукта ко многим потребителям этого продукта;
3) модель распределительной (лямбда) задачи линейного программирования - часто ее называют обобщенной транспортной задачей, которая заключается в использовании взаимозаменяемых ресурсов;
4) модель ассортиментной задачи линейного программирования- ее можно решать на основе системы ограничений общей или распределительной задачи линейного программирования. Особенность целевой функции состоит в том, что ставится задача максимизации количества комплектов изделий, т.е.
![]() С= X1/K1= X2/K2=…= Xn/Kn Max, где
С= X1/K1= X2/K2=…= Xn/Kn Max, где
C- количество комплектов;
Kj- количество j-х изделий, входящих в комплект (j=1,2,..,n)
Xj- количество производимых изделий j- го вида.
В общем виде задачи распределения характеризуются следующими условиями:
1. Существует ряд операций, которые должны быть выполнены.
2. Имеется достаточное количество ресурсов для выполнения всех операций.
3. Некоторые операции можно выполнять различными способами.
4. Некоторые способы выполнения операций лучше других.
5. Имеющегося в наличии количества ресурсов недостаточно для выполнения каждой операции наилучшим способом.
Рассмотрим более подробно задачи распределения, различающихся между собой видом математических моделей и объектами исследования: задачи о назначениях, задачи использования ресурсов (или задачи собственно распределения), задачи о смесях (о диете), задачи о раскрое, транспортные задачи. Так как я буду использовать при решении задачи задачу собственно распределения, то остановлюсь на ней более подробно().
Задача о смесях (о диете)
К задачам о диете относятся задачи, в которых требуется выбрать самый дешевый пищевой рацион, содержащий необходимое количество указанных заранее питательных веществ. Предполагается, что:
1. известен перечень биологически необходимых питательных веществ и их минимальная норма (например, суточная);
2. задан набор продуктов, из которых требуется составить пищевой рацион;
3. имеются нормы содержания различных питательных веществ в единице соответствующего продукта;
4. известна цена единицы каждого продукта, который может быть использован в пищевом рационе. Подобная проблема возникает при выборе рационального корма для скота.
Формализуем описанную ситуацию:
Будем считать, что в рацион должно входить m биологически необходимых питательных веществ (индекс i). Таким образом, i=1,2,..,m.
Известно, что i-го питательного вещества в рационе должно быть не меньше, чем biединиц. Предположим, что мы располагаем n различными продуктами, из которых составляется пищевой рацион (индекс j, j=1,2,…,n). Норму содержания i-го питательного вещества в j-ом продукте обозначим через aij. Нам известна таблица-матрица, состоящая из m×n чисел aij.
Таблица 2.1.1
| Пищевые продукты | |||||
| 1 | 2 | … | n | ||
| Питательные вещества | 1 | a11 | a12 | … | a1n |
| 2 | a21 | a22 | … | a21 | |
| ... | … | … | … | … | |
| … | … | … | … | … | |
| m | am1 | am2 | … | amn | |
Цены, которые установлены на продукты питания, обозначим cj за единицу j-го продукта. Количество j-го продукта, входящего в пищевой рацион, обозначим через xj.
В этих обозначениях выбор самого дешевого рациона, удовлетворяющего сформулированным выше требованиям, сводится к решению следующей математической задачи:
Найти вектор X = ( x1, x2, …, xn), удовлетворяющий системе ограничений:
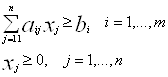
и доставляющий целевой функции ![]() минимальное значение.
минимальное значение.
Ограничение для каждого i означает, что в выбираемом рационе i-го питательного вещества должно содержать не менее, чем bi единиц. Второе ограничение формализует тот факт, что j-ый продукт может либо входить в рацион, и тогда xi>0, либо не входить, и тогда xi =0.
2.2 Методы решения задач о смесях
экономическая математическая задача интегрированная
От того, как будут распределяться ограниченные ресурсы, зависит конечный результат деятельности бизнеса, т. е., успешность решения подавляющего большинства экономических задач зависит от наилучшего способа использования ресурсов.
В результате чего и разработали методы решения данных задач, называемых оптимизационными методами задач распределения, основные из них: симплекс-метод, двойственный симплекс-метод, метод искусственного базиса, графический метод и решение задач средствами Excel через «Поиск решений». Так как я во втором разделе буду использовать при решении задачи распределения симплекс-метод, то рассмотрю его подробнее.
Симплекс-метод
Классическим методом решения рада линейного программирования стал симплекс-метод, получившим также в литературе название метода последовательного улучшения плана. Этот метод был разработан в 1947 г. американским математиком Джорджем Данцигом. Этот метод может быть использован для решения большого комплекса задач внутризаводского планирования: формирование специфицированной годовой производственной программы выпуска предприятия, плана загрузки различных групп оборудования, календарное распределение производственной программы выпуска и т.д.
Сточки зрения рациональности и наглядности вычислительного процесса выполнение алгоритма симплекс-метода удобно оформлять в виде последовательности таблиц. В различных источниках приводятся разные модификации симплекс таблиц, отличающихся друг от друга расположением отдельных элементов. Однако все они базируются на одних и тех же принципах. Основная идея симплекс-метода состоит в следующем:
1) принимается за базу одна из возможных программ - отправная (опорный план);
2) осуществляется ее пошаговое улучшение, пока не будет получен оптимум по заданной критериальной функции.
Т.о. проблема сводится к определению отправного варианта программы и нахождению способа улучшения последнего. При этом при формировании начального варианта программы создается как бы запас, возможность реализации в виде резервов тех ресурсов, которые регламентируются в сложившейся производственной ситуации. В процессе преобразований одни переменные вводятся в план, другие исключаются из него. С каждым шагом план приближается к оптимальному и в конечном счете приходит к нему, если в условиях задачи нет противоречия. За счет пошагового распределения ресурсов между планируемыми на выпуск изделиями (деталями) находится такое сочетание номенклатуры и количества этих изделий, которое является наилучшим с точки зрения достижения заданного критерия оптимальности и использования имеющихся ресурсов.
Решение задач симплекс-методом предусматривает выполнение следующих процедур:
1) формирование целевой функции;
2) определение ограничительных условий – функциональных ограничений, которые могут иметь вид неравенств;
3) преобразование ограничений из неравенств в систему равенств путем ввода вспомогательных, свободных переменных (последние имеют экономическое содержание и характеризуют резерв, неиспользованный остаток тех ресурсов, по которым введено ограничение);
4) построение исходной симплексной таблицы, в которой в формируемый план входят только свободные переменные;
5) ввод в исходный вариант плана реальных переменных и прежде всего тех, которые в наибольшей степени реализуют целевую функцию;
6) определение числового значения вводимой переменной – величины программы.
При этом каждый из показателей, характеризующих ограничительное условие, делится на соответствующий коэффициент при вводимом переменном – удельный расход данного ресурса. Тогда наименьшее частное определит максимально возможное в условиях принятых ограничений использование ресурсов при заданном критерии оптимальности. Полученный результат вводится в соответствующую строку формируемого плана симплексной таблицы. На этой строке матрицы весь ресурс исчерпан, она является «узким местом» и подлежит выводу. На ее место вводится другая строка, предварительно пересчитанная. Формируется новый вариант симплексной таблицы.
После каждой симплексной таблицы анализируется оптимальность полученного решения. Если все элементы последней строки (Z-строки) положительны и задача на максимум, то решение оптимально. Если все элементы Z-строки отрицательны и задача на минимум, то решение оптимально. Если план неоптимальный, производится его дальнейшее улучшение.
Алгоритм решения задачи симплекс-методом. Формирование целевой функции и системы ограниченных условий.
1. Перевод неравенств в систему равенств.
2. Построение исходной симплекс-таблицы
Таблица 2.2.1
| Базис | Ci+n | C1 | C2 | … | Cn | Cn+1 | Cn+2 | … | Cn+m | Bj |
x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+m | |||
xn+1 | Cn+1 | a11 | a12 | … | a1n | 1 | 0 | … | 0 | b1 |
xn+2 | Cn+2 | a21 | a22 | … | a2n | 0 | 1 | … | 0 | b2 |
| … | … | … |
