Эконометрическое моделирование временных рядов
Задача 1
За год на предприятии были выпущены семь партий продукции, для каждой из которых были определены издержки. Вычислить сумму издержек для следующего плана выпуска.
линейный экономический моделирование
Таблица 1.1.Данные о планируемом выпуске изделий
| ед.прод. тыс.шт. | затраты, руб. |
| 2,2 | ? |
| 3,9 | ? |
| 5,5 | ? |
Таблица 1.2.Данные о выпущенных партиях
| ед.прод.тыс.шт. | затраты, руб. |
| 1 | 30 |
| 2 | 70 |
| 4 | 150 |
| 3 | 100 |
| 5 | 170 |
| 6 | 215 |
| 8 | 290 |
Задача относится к разделу Парная регрессия, т.к. в ней даны один независимый параметр (единицы продукции, обозначим как х) и зависимый параметр (затраты, обозначим у).Прежде чем выбирать вид аппроксимирующей зависимости следует представить исходные данные графически.
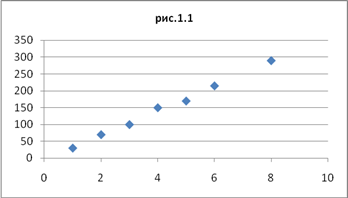
Предполагаем линейную зависимость между х и у
Y=a+bx
Для определения параметров a,b используем метод наименьших квадратов
∑( y –(a+bx))² → min
Функция минимальна, если равны нулю ё, частные производные по параметрам т.е.:
y’a = ∑ (2( y-abx)(-1))=0
y’b = ∑ (2 ( y-a-bx)(-x))=0
или
na+b∑x =∑y,
a ∑x +b ∑x² =∑xy (1)
Система уравнений (1) однозначно определяет параметры a и b – это система двух уравнений с двумя неизвестными. Все остальные величины можно определить из исходных данных :
n- количество исходных точек,
∑x ∑y - суммарные значения параметров х и у по всем точкам,
∑xy - суммарное значение произведения параметров,
∑x²- суммарное значение квадрата величины х.
Рассчитаем коэффициенты линейного уравнения парной регрессии:
Σx^2 = (x^2) - cp –(xcp)^2
b = (cp(y*x) – cp (y)*cp (x))/(σx^2) (2)
a = cp( y) - b*cp(x)
Где индекс cp обозначает среднее значение данной величины, т.е. суммарное значение данной величины надо разделить на n.
Составим таблицу в редакторе Excel.
Таблица 1.3
| n | x | y | xy | x^2 |
| 1 | 1 | 30 | 30 | 1 |
| 2 | 2 | 70 | 140 | 4 |
| 3 | 4 | 150 | 600 | 16 |
| 4 | 3 | 100 | 300 | 9 |
| 5 | 5 | 170 | 850 | 25 |
| 6 | 6 | 215 | 1290 | 36 |
| 7 | 8 | 290 | 2320 | 64 |
| итого | 29 | 1025 | 5530 | 155 |
| среднее | 4,14 | 146,43 | 790,00 | 22,14 |
| σ² | 4,98 |
Используя из табл. 1.3, получаем следующую систему уравнений:
7a+29b=1025
29a+155b=5530
Решаем систему уравнений методом последовательных исключений переменных или по формуле (2) и определяем коэффициенты
a= -6.127
b= 36.824
линейное уравнение запишем в виде
y=-6.127+36.824x (3)
Для варианта х=2,у=9 ,z =5 рассчитываем затраты
Таблица 1.4
| ед.прод. тыс.шт. | затраты, руб. |
| 2,2 | 74,89 |
| 3,9 | 137,49 |
| 5,5 | 196,41 |
Используя пакет прикладных программ (ППП) статистическая функция ЛИНЕЙНАЯ и графические результаты (добавить линию тренда) проверим полученные результаты.
Таблица 1.5
| 36,824 | -6,127 |
| 0,987 | 4,64432 |
| 0,9964 | 5,82708 |
| 1392 | 5 |
| 47266 | 169,775 |
Рис.1.2.
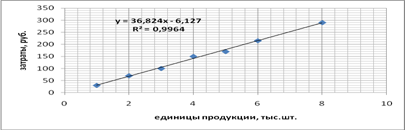
Кроме того, по найденному уравнению линейной регрессии (3) проведем расчет величин у, сравним их с заданными, т.е. рассчитаем отклонения и определим их суммарное отклонение, которое должно быть равно нулю. Результаты приведем в табл. 1.6.
Таблица 1.6
| n | x | y | xy | y² | x² | y расч | y-y расч |
| 1 | 1 | 30 | 30 | 900 | 1 | 30,7 | -0,7 |
| 2 | 2 | 70 | 140 | 4900 | 4 | 67,5 | 2,5 |
| 3 | 4 | 150 | 600 | 22500 | 16 | 141,2 | 8,8 |
| 4 | 3 | 100 | 300 | 10000 | 9 | 104,3 | -4,3 |
| 5 | 5 | 170 | 850 | 28900 | 25 | 178,0 | -8,0 |
| 6 | 6 | 215 | 1290 | 46225 | 36 | 214,8 | 0,2 |
| 7 | 8 | 290 | 2320 | 84100 | 64 | 288,5 | 1,5 |
| итого | 29 | 1025 | 5530 | 197525 | 155 | 0,0 |
Выводы:
1. Решена задача парной регрессии методом наименьших квадратов.
2. Получены коэффициенты в линейном уравнении y=-6.127+36.824x и рассчитан возможный домашний вариант.
3. Результаты проверены с помощью ППП и линии тренда.
Задача 2.
По семи территория Уральского района за 1995 г. Изе6стны значения двух признаков (табл.2.1)
Таблица 2.1
| район | расходы на покупку продовольственных товаров в общих расходах, % у | среднедневная заработная плата одного работающего, руб.,х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется определить параметры парной регрессии для следующих функции: линейной степенной показательной, равносторонней геперболы и параболы методом наименьших квадратов (МНК). Составить прогноз величины у для некоторого х например для х=1.1 (х) min. Дать графическую интерпретацию результатов, использовать ППП для решения статистических задач сделать выводы.
К исходным данным добавим ещё одну пару значений х,у, связанную с порядковым номером по журналу и количеством студентов в группе, по формулам:
x8=xmin +((xmax-xmin)/Nсум)*Ni
y8=ymin+((ymax-ymin)/Nсум)*Ni
где, Ni –порядковый номер по журналу, Nсум- количество студентов в группе, min, max – минимальная и максимальная величины х и у по таблице 2.1.
после этого составляем таблицу 2.2 и рассчитываем все параметры для решения системы уравнений:
na+b∑x =∑y (4)
a∑x+b∑(x^2) =∑(xy)
Рассчитываем коэффициенты линейного уравнения парной регрессии:
σx^2= (x^2)cp = (xcp)^2
b= (cp(y*x) –cp(y)*cp(x))/(σx^2) (5)
a= cp (y) –b*cp(x)
Таблица 2.2.Линейная регрессия y=a+bx
