Электродинамика
Магнитное поле.
В пространстве, окружающее токи и постоянные магниты, возникает силовое поле – магнитное.
Его наличие обнаруживается по сильному воздействию на внесённые в него проводники с током и постоянные магниты.
Рамка с током ориентируется в магнитном поле. Её можно использовать для количественного описания магнитного поля.
(Рисунок)
Вращающий момент сил:
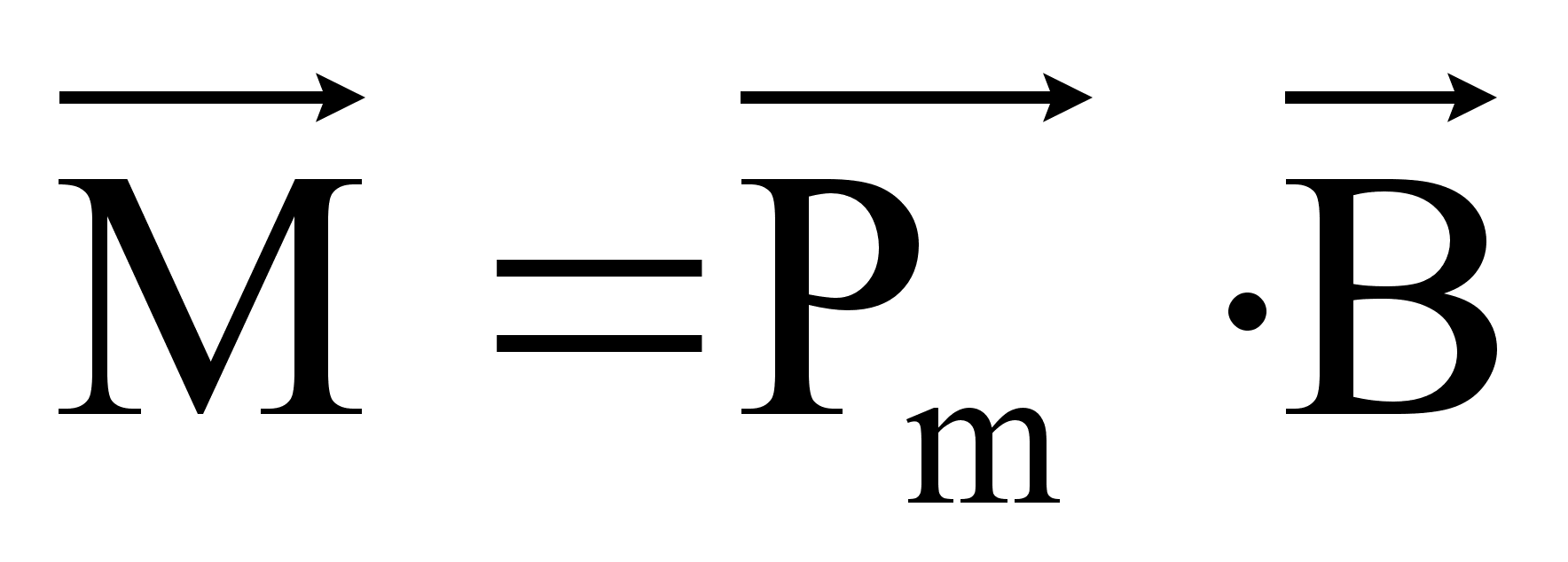 (50)
(50)
где 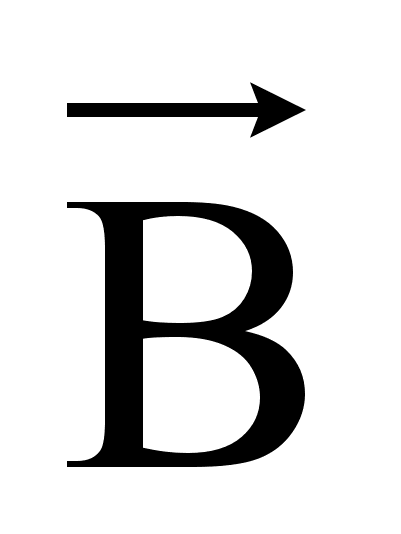 - вектор магнитной индукции,
- вектор магнитной индукции,
 - вектор магнитного момента.
- вектор магнитного момента.
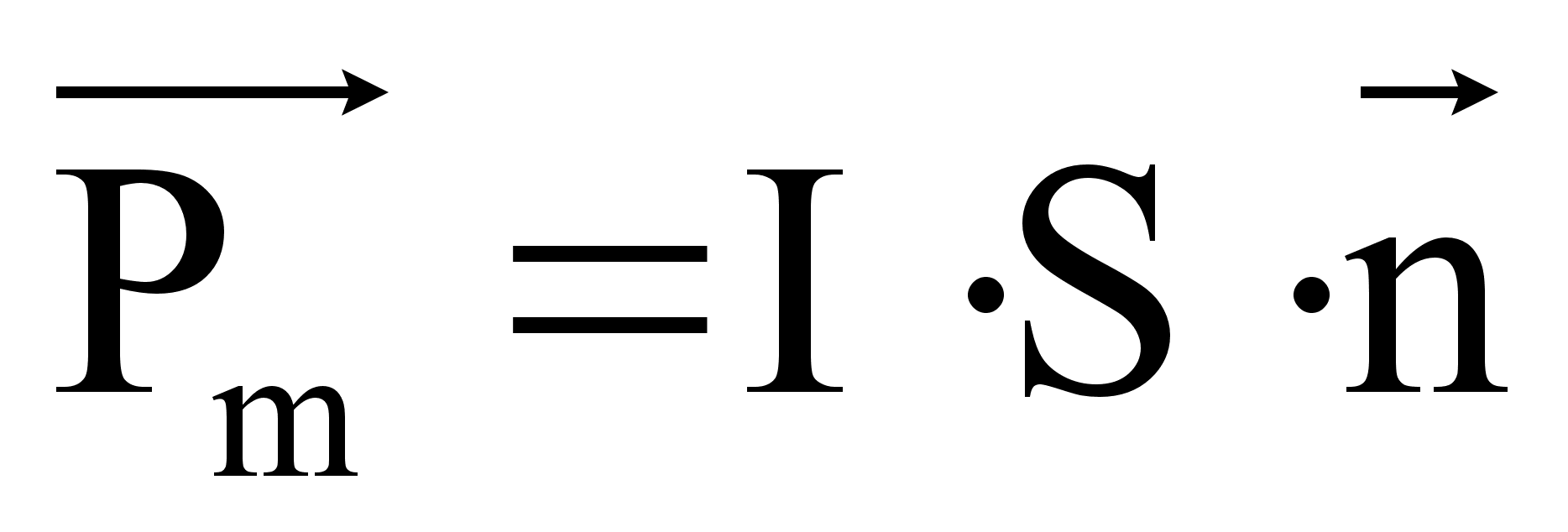 (51)
(51)
где 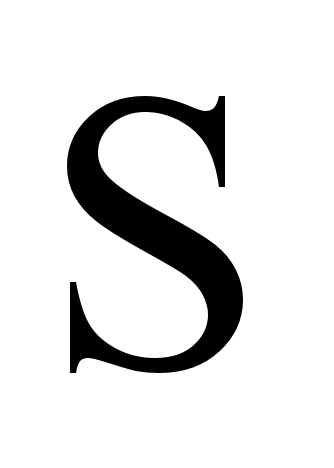 - площадь рамки
- площадь рамки
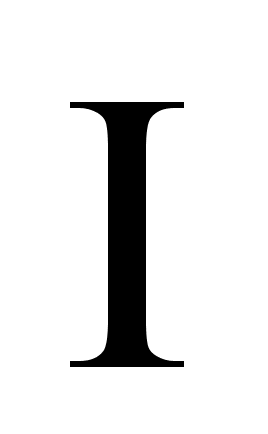 - сила тока
- сила тока
 - единичный вектор в направлении нормали рамки.
- единичный вектор в направлении нормали рамки.
Из выражений (50) и (51) следует, что вращающий момент М пропорционален силе тока 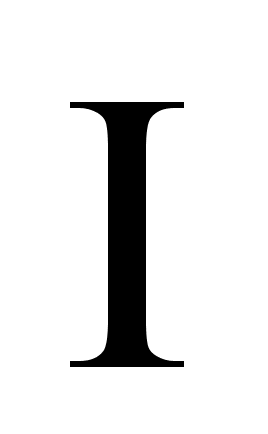 и площади рамки
и площади рамки 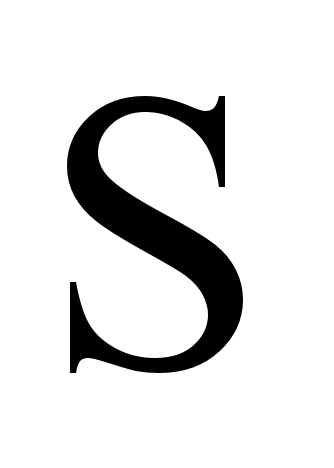 . Таким образом, для другой точки стационарного магнитного поля вектор магнитной индукции будет величиной неизменной.
. Таким образом, для другой точки стационарного магнитного поля вектор магнитной индукции будет величиной неизменной.
Движущиеся заряды (токи) изменяют свойства окружающей их среды, то есть создают магнитное поле.
Вектор магнитной индукции 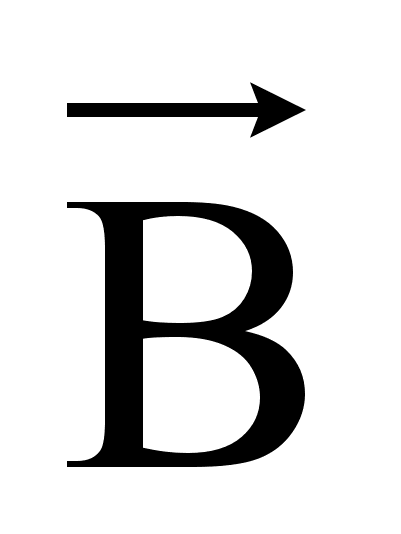 характеризует магнитное поле с учётом магнитных свойств среды.
характеризует магнитное поле с учётом магнитных свойств среды.
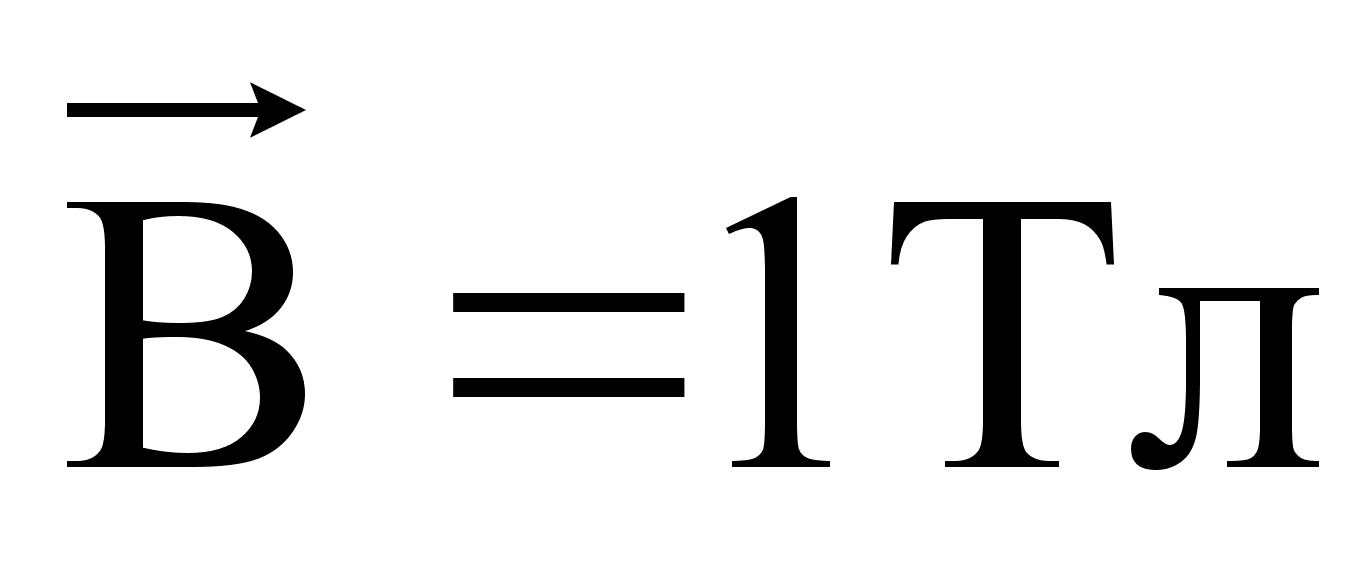
Вектор напряжённости магнитного поля  магнитное поле как функцию от электрического тока, создавшего это поле и от расстояния до тока от рассматриваемой точки поля, то есть без учёта магнитных свойств среды.
магнитное поле как функцию от электрического тока, создавшего это поле и от расстояния до тока от рассматриваемой точки поля, то есть без учёта магнитных свойств среды.
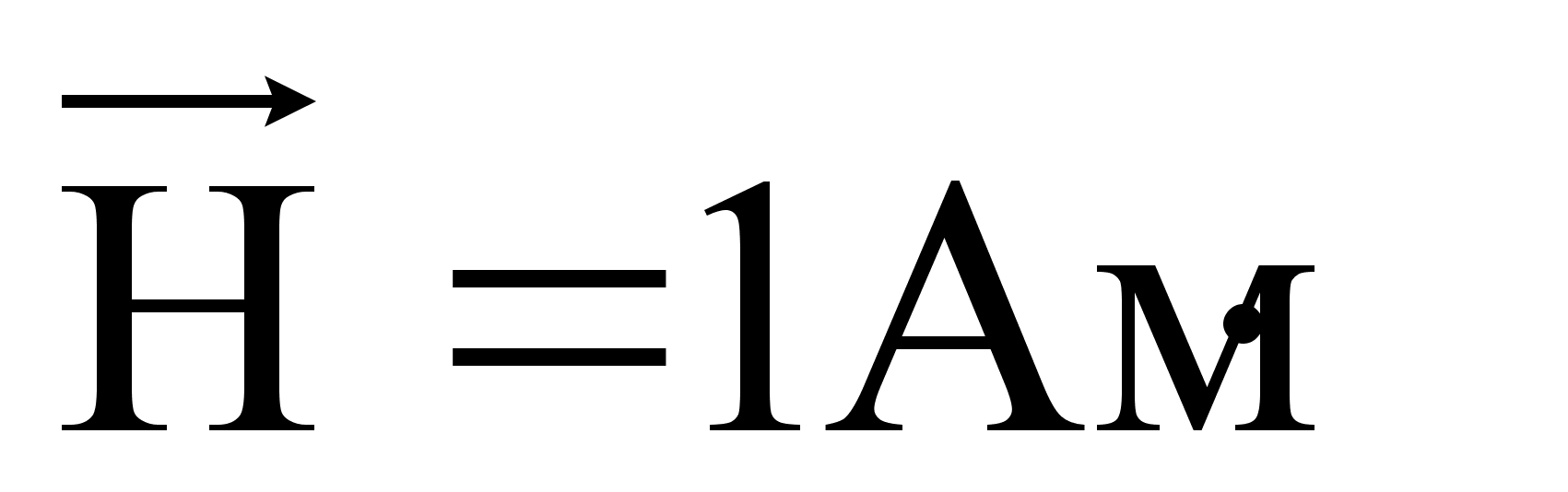
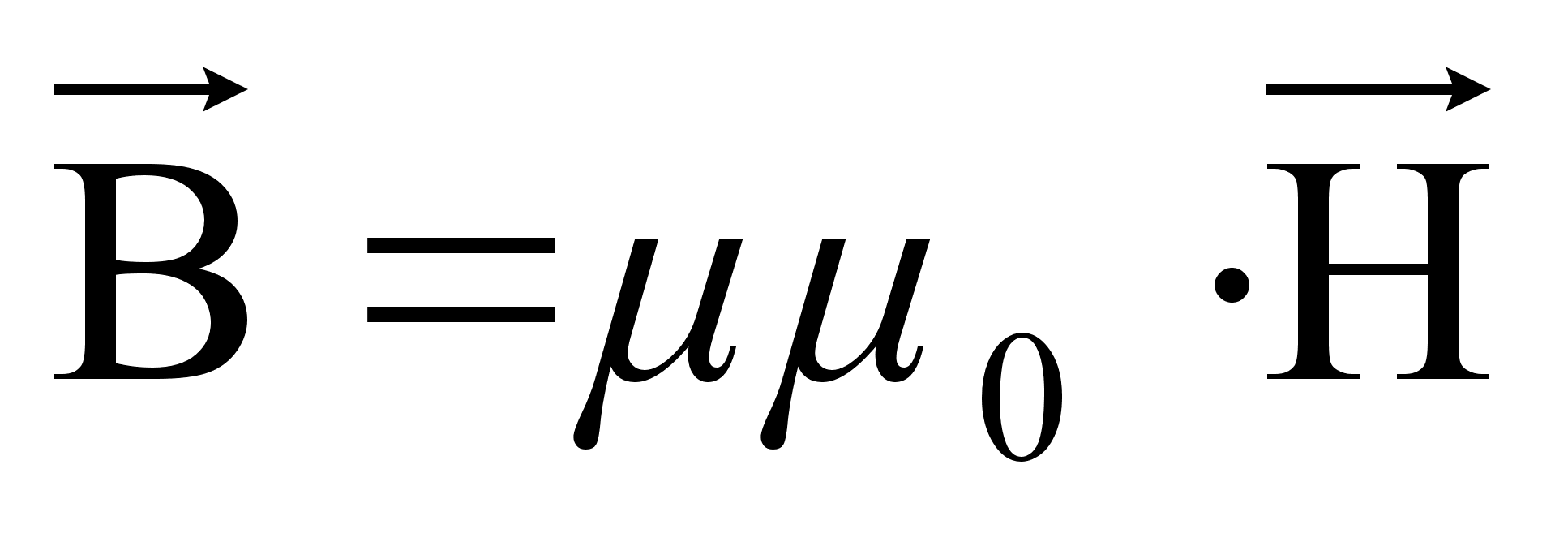 (52)
(52)
где 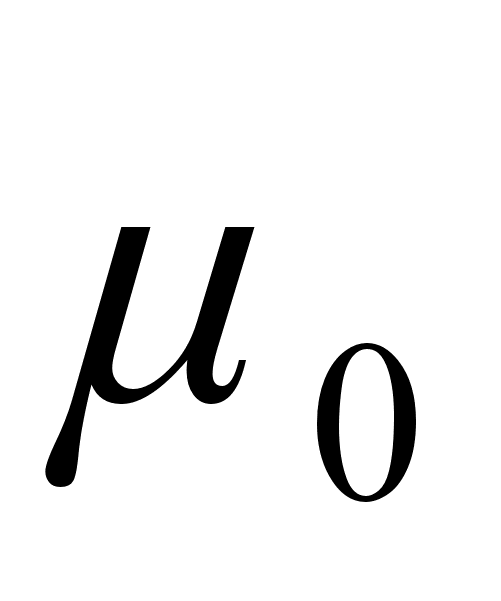 - магнитная постоянная (характеризует магнитные свойства вакуума
- магнитная постоянная (характеризует магнитные свойства вакуума
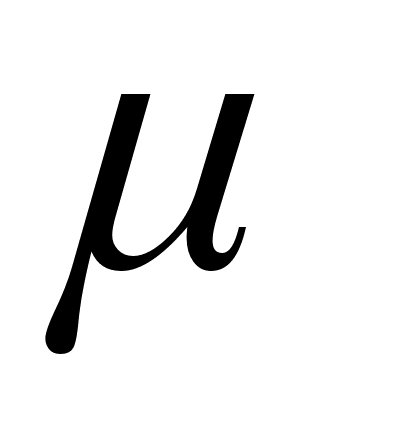 - магнитная проницаемость среды ( показывает во сколько раз усиливается магнитное поле в среде за счёт ориентации атомов и молекул во внешнем магнитном поле).
- магнитная проницаемость среды ( показывает во сколько раз усиливается магнитное поле в среде за счёт ориентации атомов и молекул во внешнем магнитном поле).
Так как магнитное поле является силовым, то его изображают линиями магнитной индукции 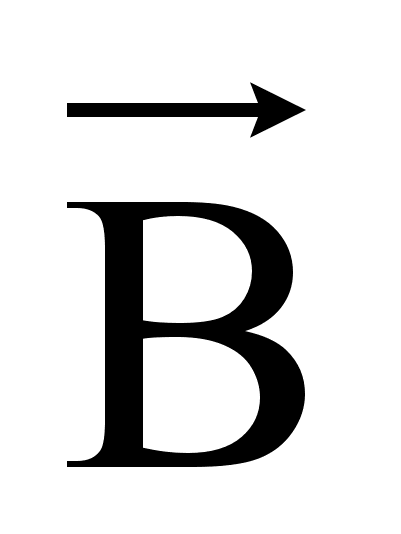 .
.
(Рисунок)
Линии магнитной индукции всегда замкнуты.
Поле, обладающее замкнутыми силовыми линиями, называют вихревым.
Поток вектора 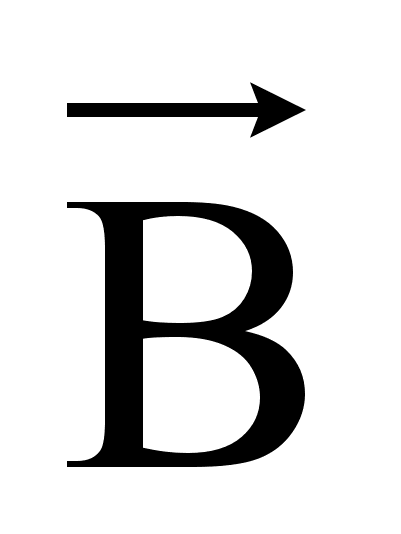 (магнитный поток) через площадку
(магнитный поток) через площадку 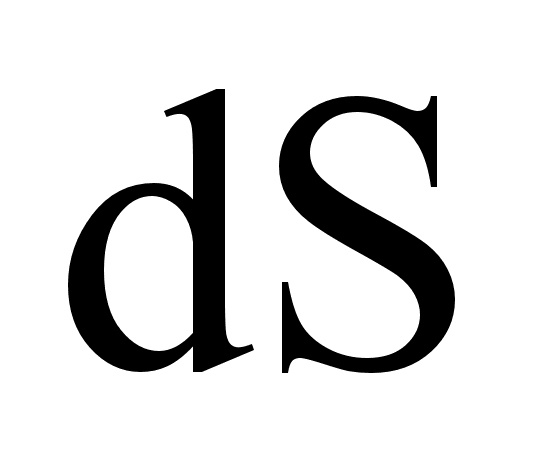 :
:
 (53)
(53)
или 
Из опыта следует принцип суперпозиции:
Магнитное поле, созданное несколькими токами или движущимися зарядами равно векторной сумме полей, создаваемых каждым током или движущимся зарядом в отдельности:
 (54)
(54)
Магнитноеполе в веществе.
Всякое вещество является магнетиком, то есть способно намагничиваться под действием магнитного поля. Это явление объясняется тем, что электроны, входящие в состав атомов (молекул) создают при своём движении круговые токи. Каждый такой ток создаёт вокруг себя магнитное поле (обладает магнитным моментом).
(Рисунок)
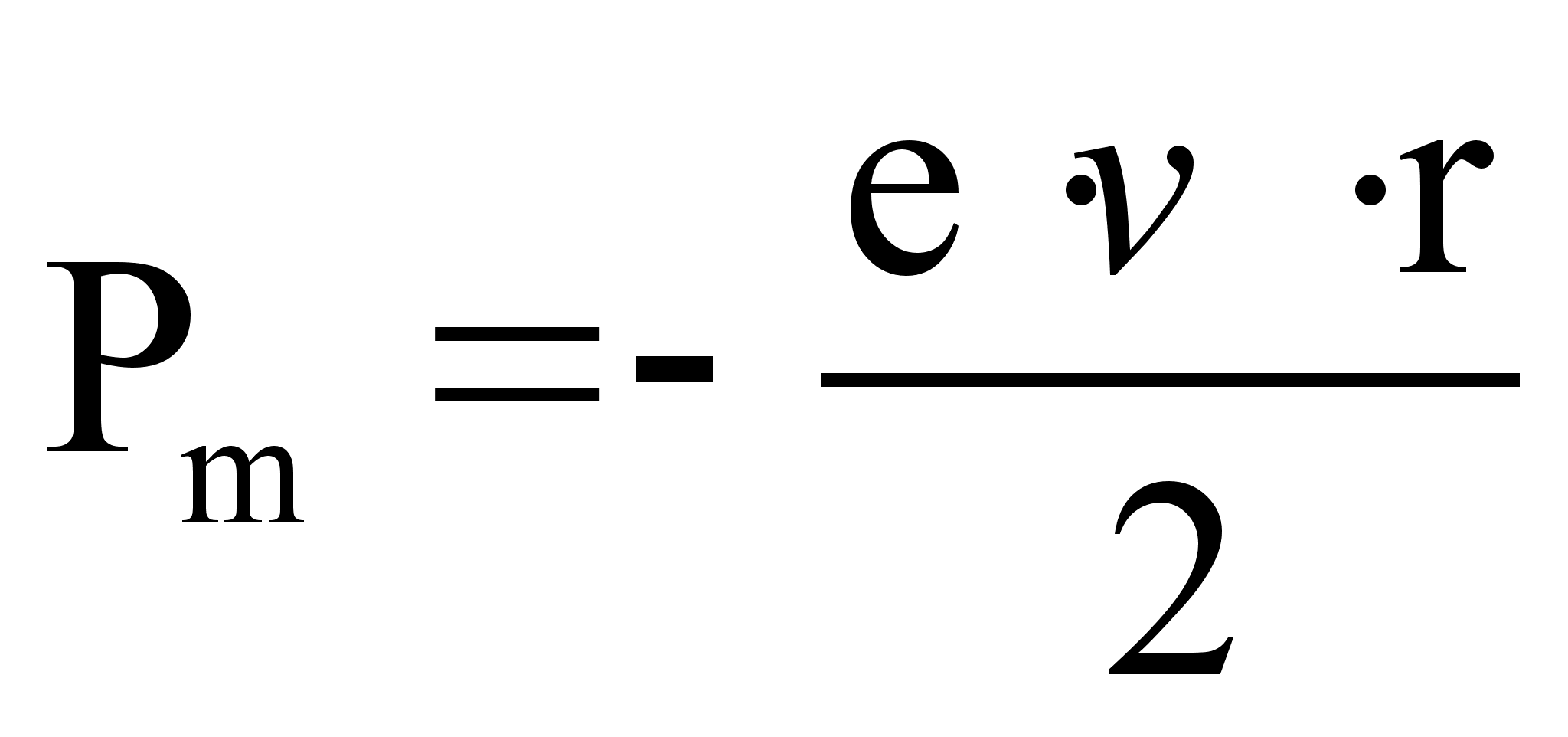 - модуль магнитного момента
- модуль магнитного момента
где е – заряд электрона
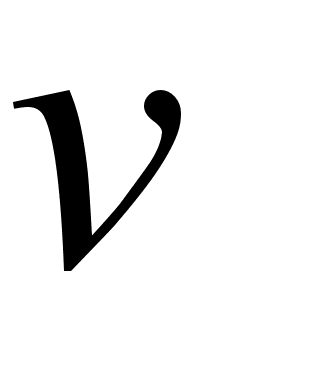 - скорость электрона
- скорость электрона
r – радиус орбиты
Без внешнего магнитного поля магнитные моменты в веществе ориентированы хаотично, вследствие теплового движения атомов и молекул. Во внешнем магнитном поле они ориентируются по полю, поэтому результирующее поле 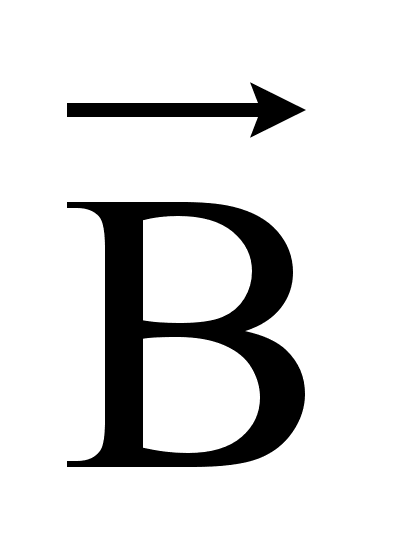 равно
равно

где 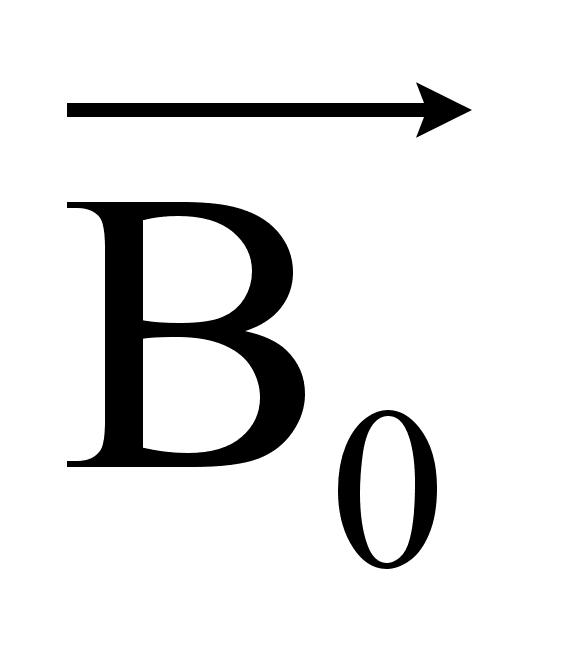 - внешнее поле
- внешнее поле
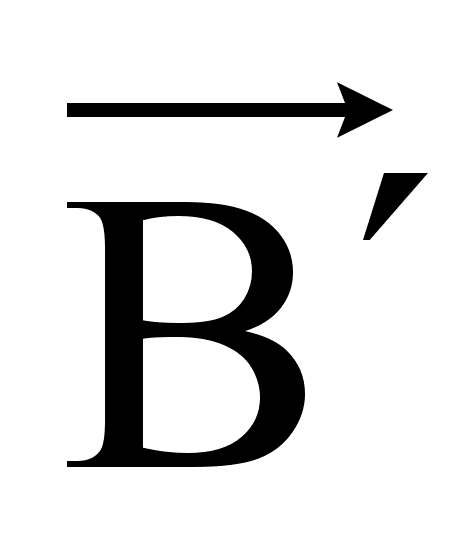 - поле, создаваемое намагниченным веществом
- поле, создаваемое намагниченным веществом
Характеристикой намагниченного магнетика является физическая величина, называемая намагниченностью - - представляет собой магнитный момент в единицу объёма.

Если магнитный момент атомов (молекул) относительно мал, то внешнее магнитное поле воздействует на электронную орбиту таким образом, что вектор магнитного момента прогрессирует относительно вектора магнитной индукции.
(Рисунок)
Это движение эквивалентно круговому току, который создаёт магнитное поле. Поле, создаваемое намагниченным веществом направлено противоположно внешнему полю и ослабевает его. Вещества, обладающие такими магнитными свойствами называются диамагнетиками.
Если магнитный момент относительно велик, то значительное число векторов 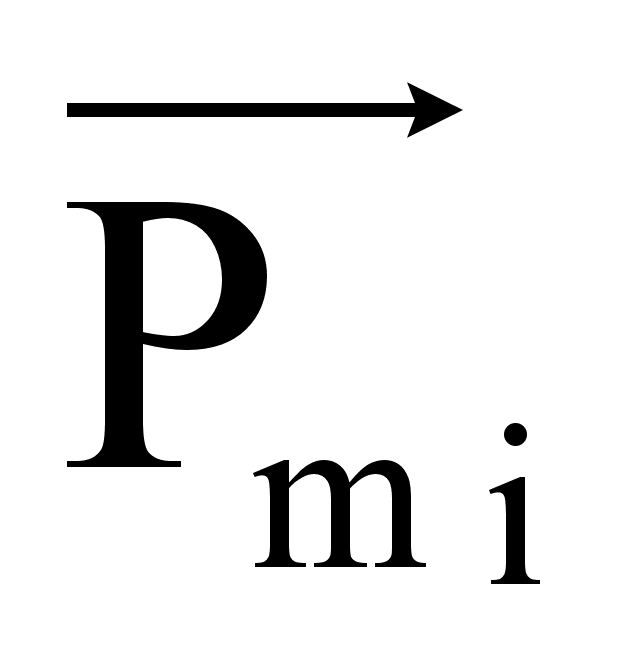 ориентируется во внешнем магнитном поле - это парамагнитный эффект.
ориентируется во внешнем магнитном поле - это парамагнитный эффект.
Диамагнитный эффект слабее парамагнитного, поэтому 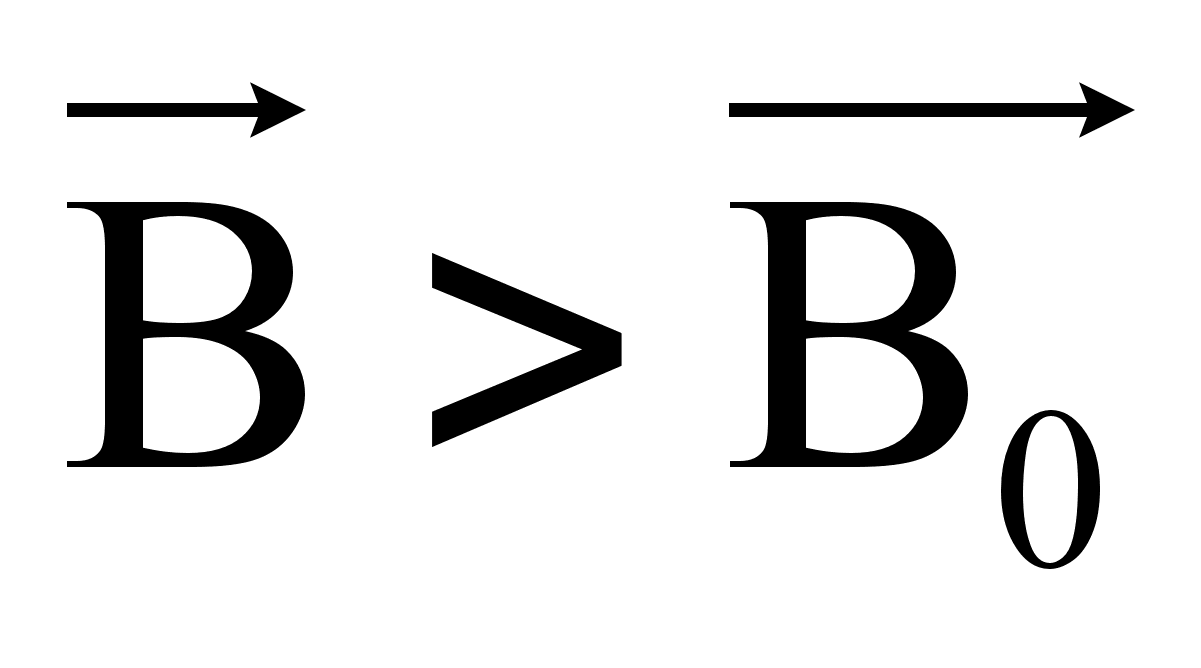 .
.
Ориентация всех магнитных моментов по внешнему магнитному полю не произойдет, так как этому мешает тепловое движение атомов (молекул). Вещества с такими свойствами – парамагнетики.
(Рисунок)
Для количественной оценки явления рассмотрим магнетик цилиндрической формы.
Вычислим индукцию магнитного поля, создаваемую молекулярным током:
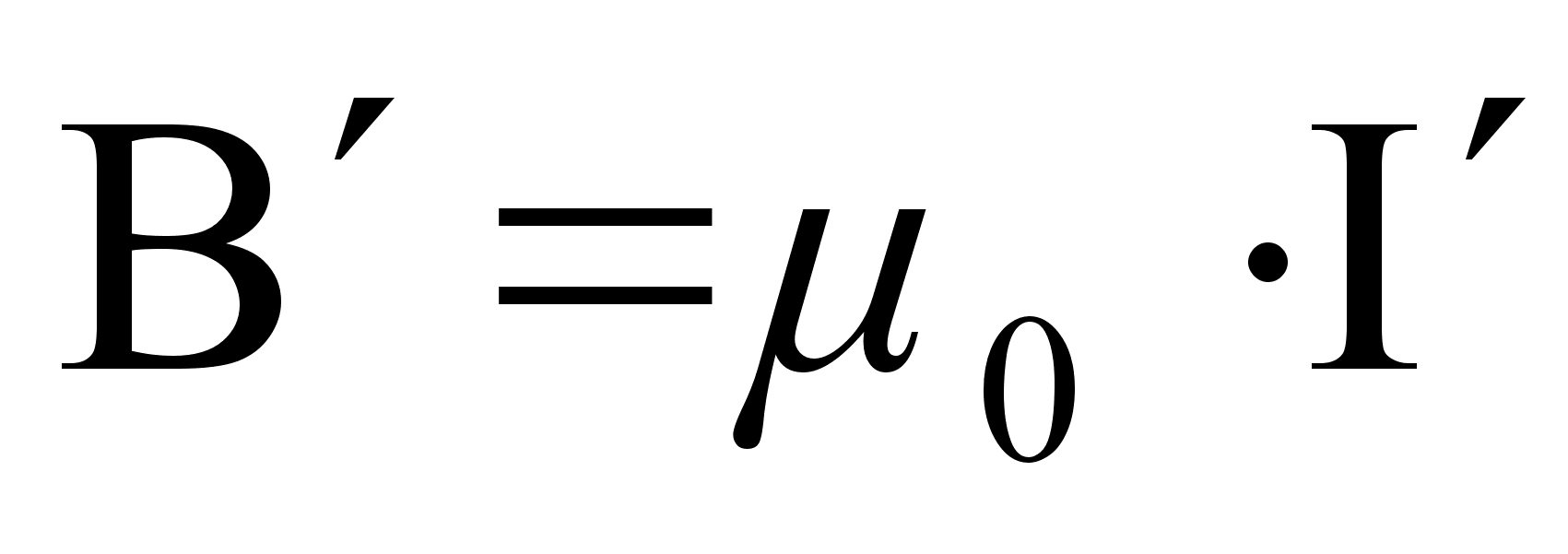
Магнитный момент этого тока:
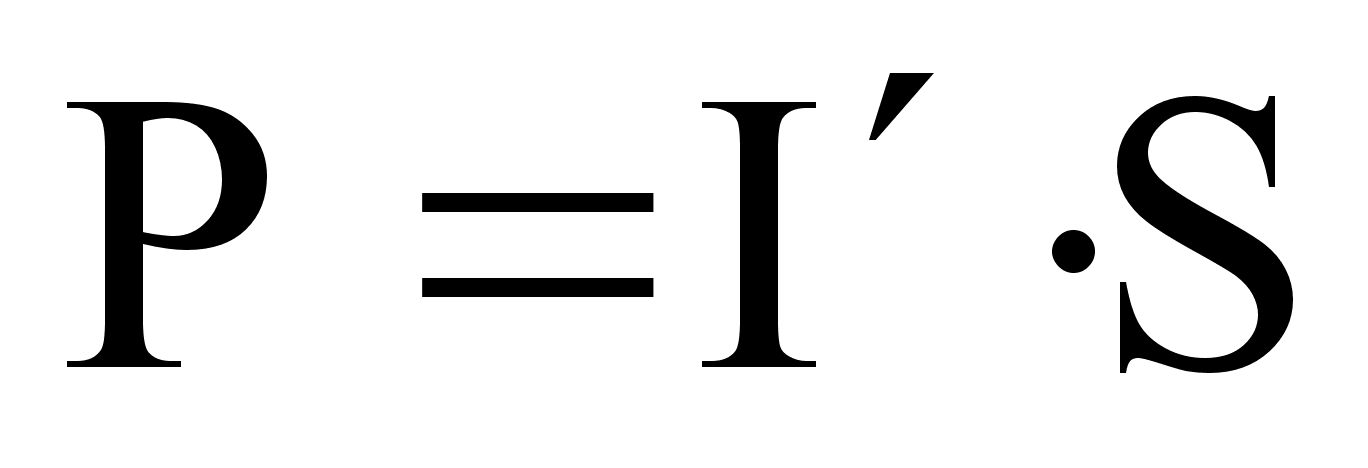
Так как длина равна 1, то, умножив на длину, получим:
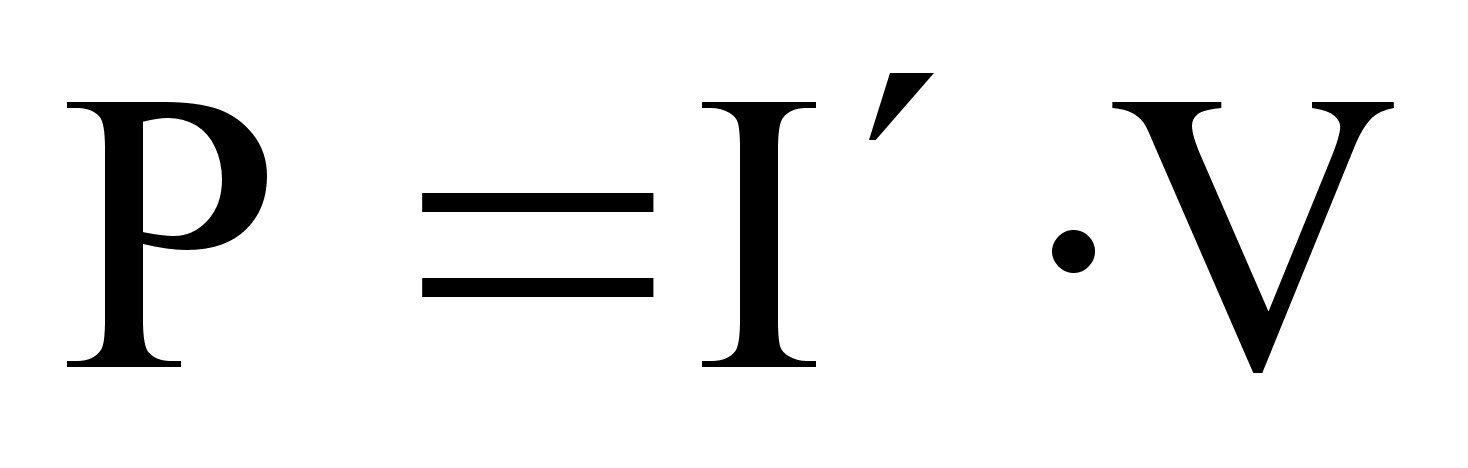 , откуда
, откуда 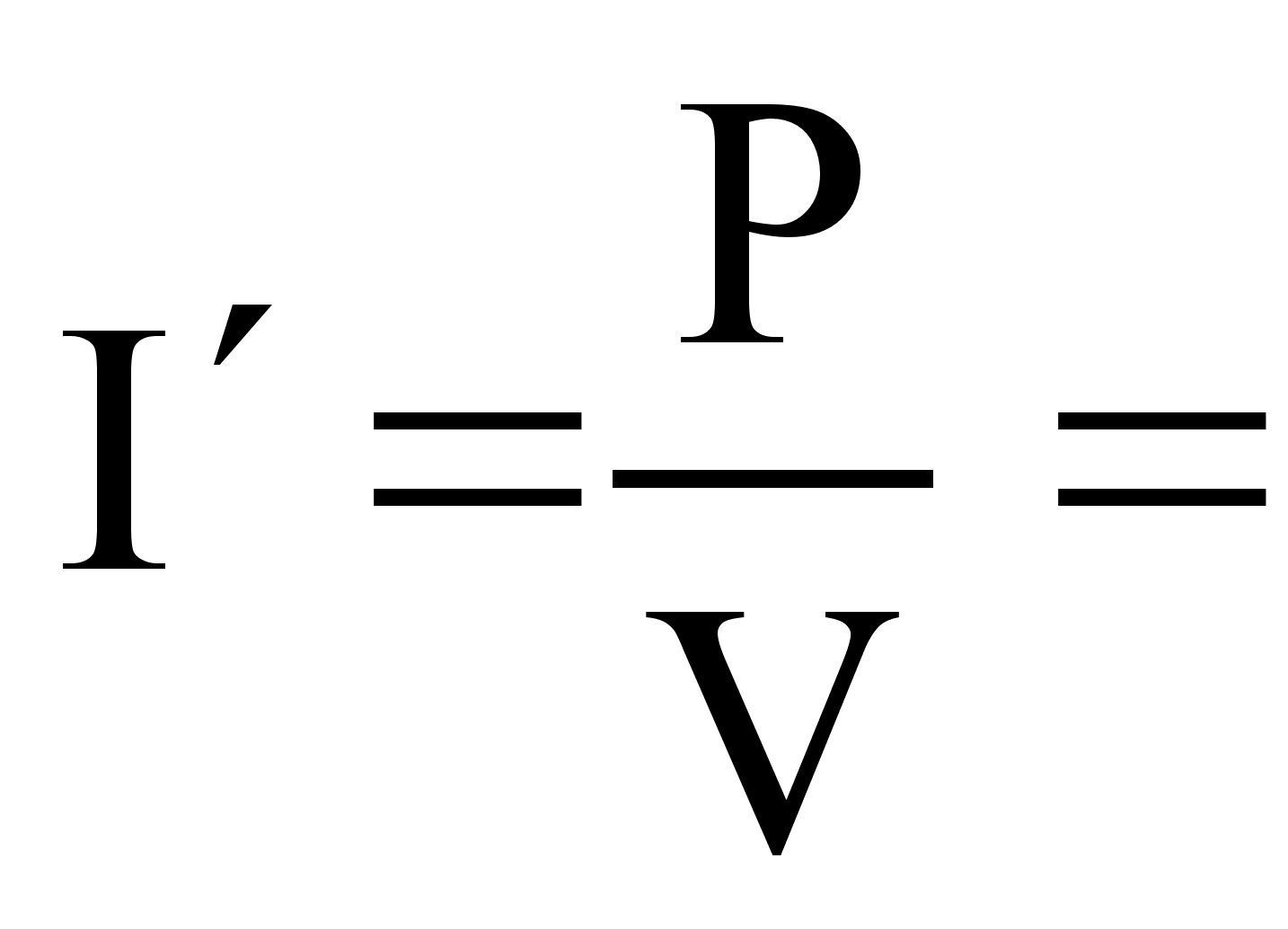
Подставив это значение в формулу для 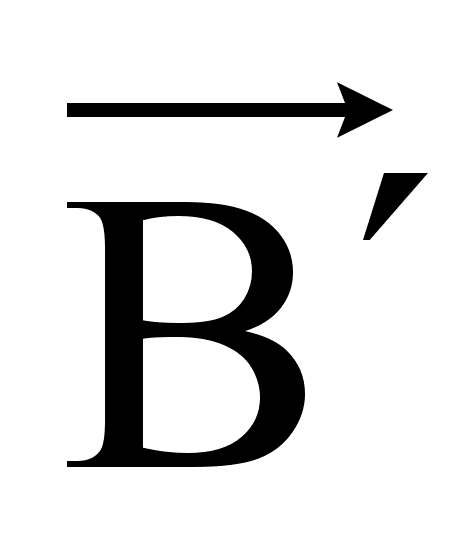 , получим:
, получим:
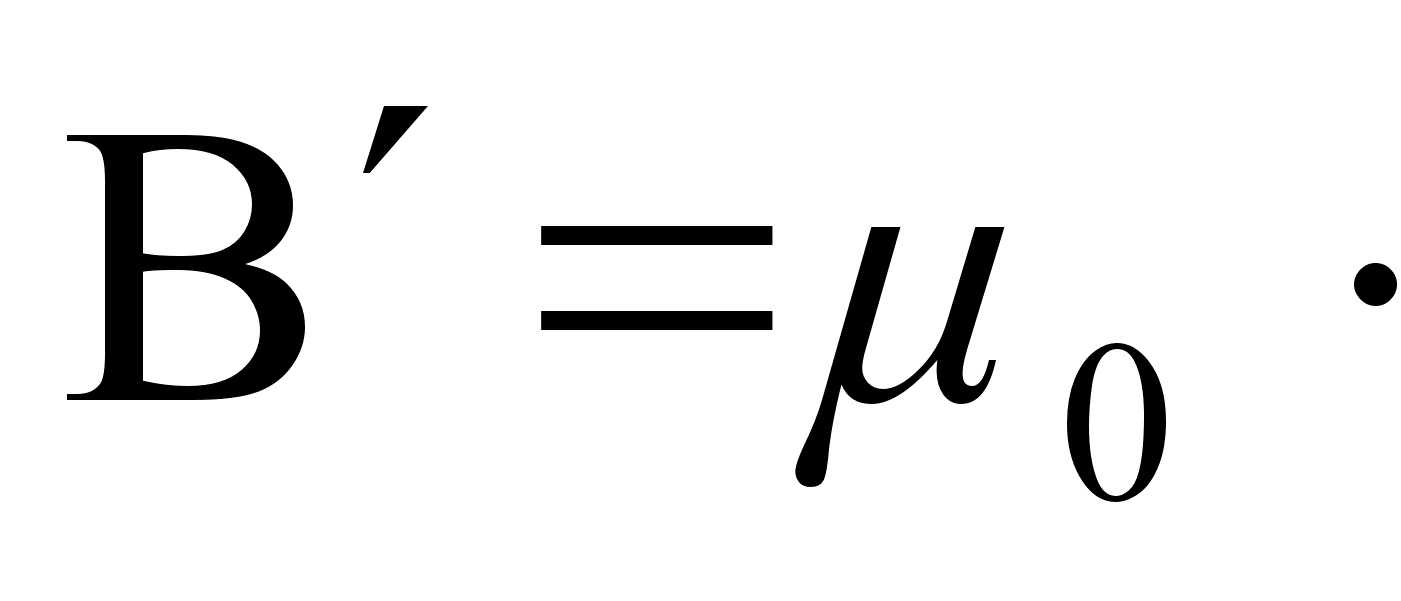
Подставим 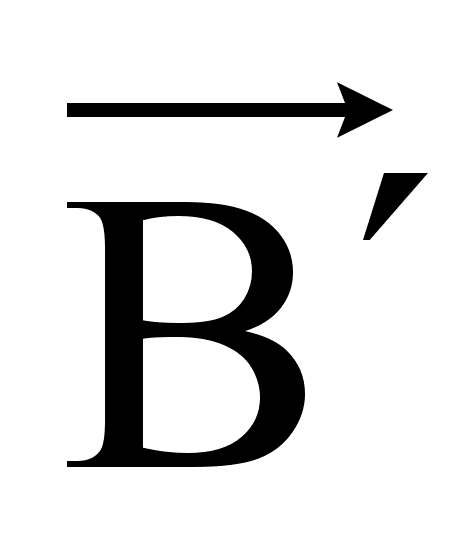 и
и 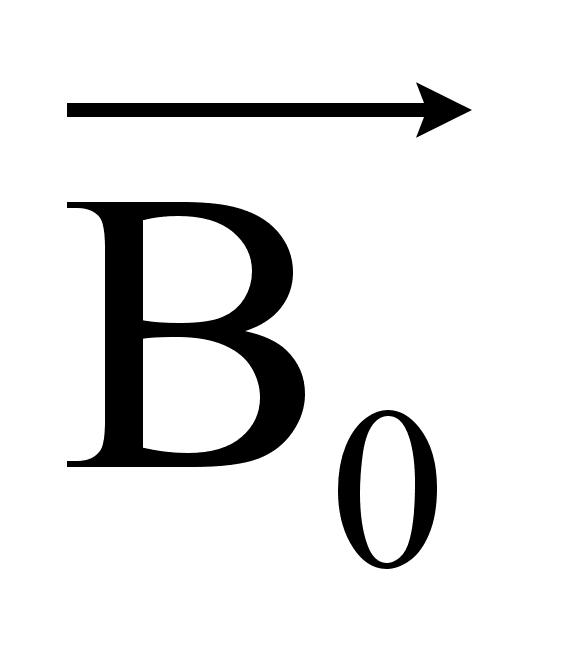 в предыдущее выражение:
в предыдущее выражение:
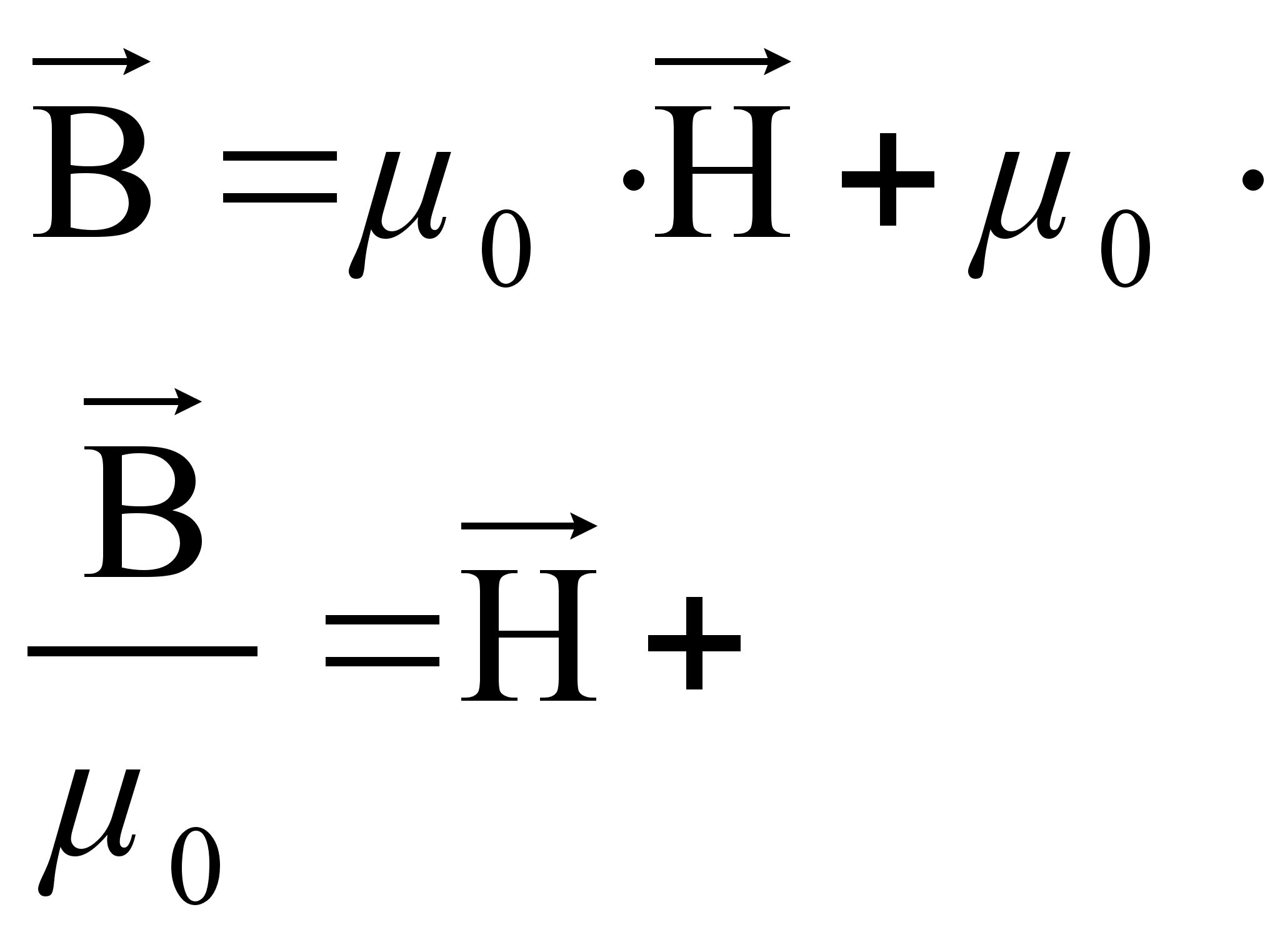
Из опыта известно, что в слабых полях намагниченность пропорциональна  , следовательно
, следовательно  , где - магнитная
, где - магнитная
Для диамагнетиков
Для парамагнетиков
Используя эту формулу, можно записать:
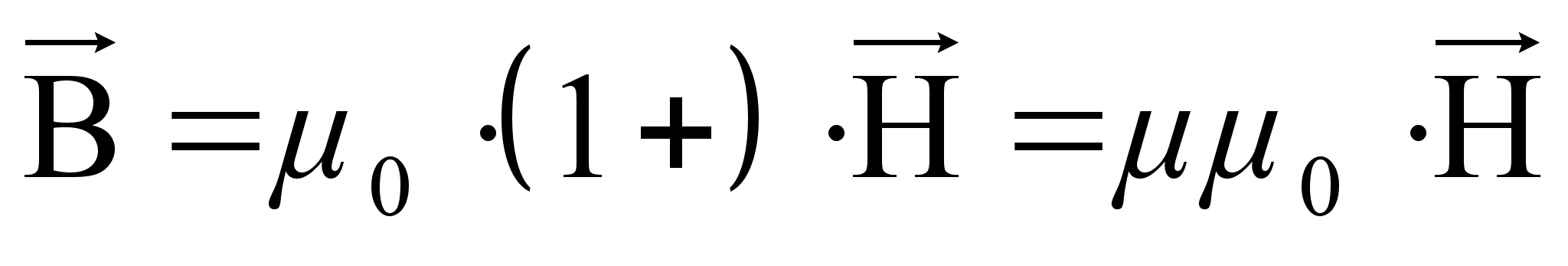
Для диамагнетиков магнитная проницаемость среды 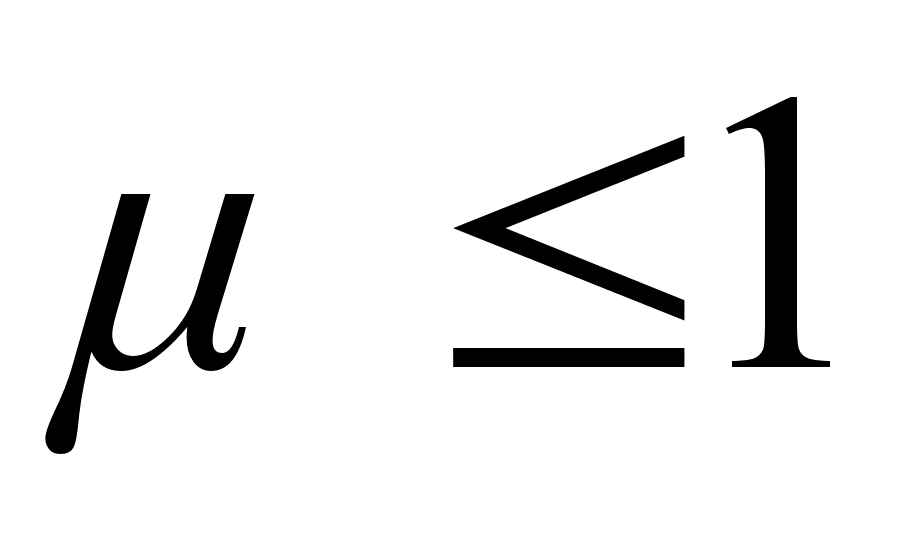
Для парамагнетиков - 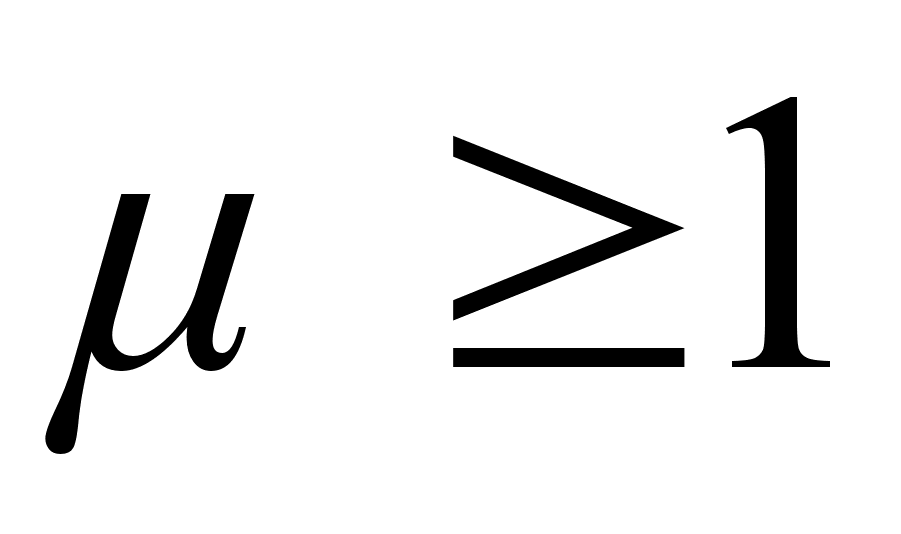 .
.
Существуют твёрдые тела, назыемые ферромагнетиками, у которых  . Объясняется это тем, что в ферромагнетиках существуют области спонтанного (самопроизвольного) намагничивания, даже слабого внешнего магнитного поля достаточно для их ориентирования по этому полю. Температура, при которой ферромагнетик теряет свои магнитные свойства и становится парамагнетиком называется точкой Кюри.
. Объясняется это тем, что в ферромагнетиках существуют области спонтанного (самопроизвольного) намагничивания, даже слабого внешнего магнитного поля достаточно для их ориентирования по этому полю. Температура, при которой ферромагнетик теряет свои магнитные свойства и становится парамагнетиком называется точкой Кюри.

Магнитное поле прямого тока
(проводник бесконечной длины).
(Рисунок)
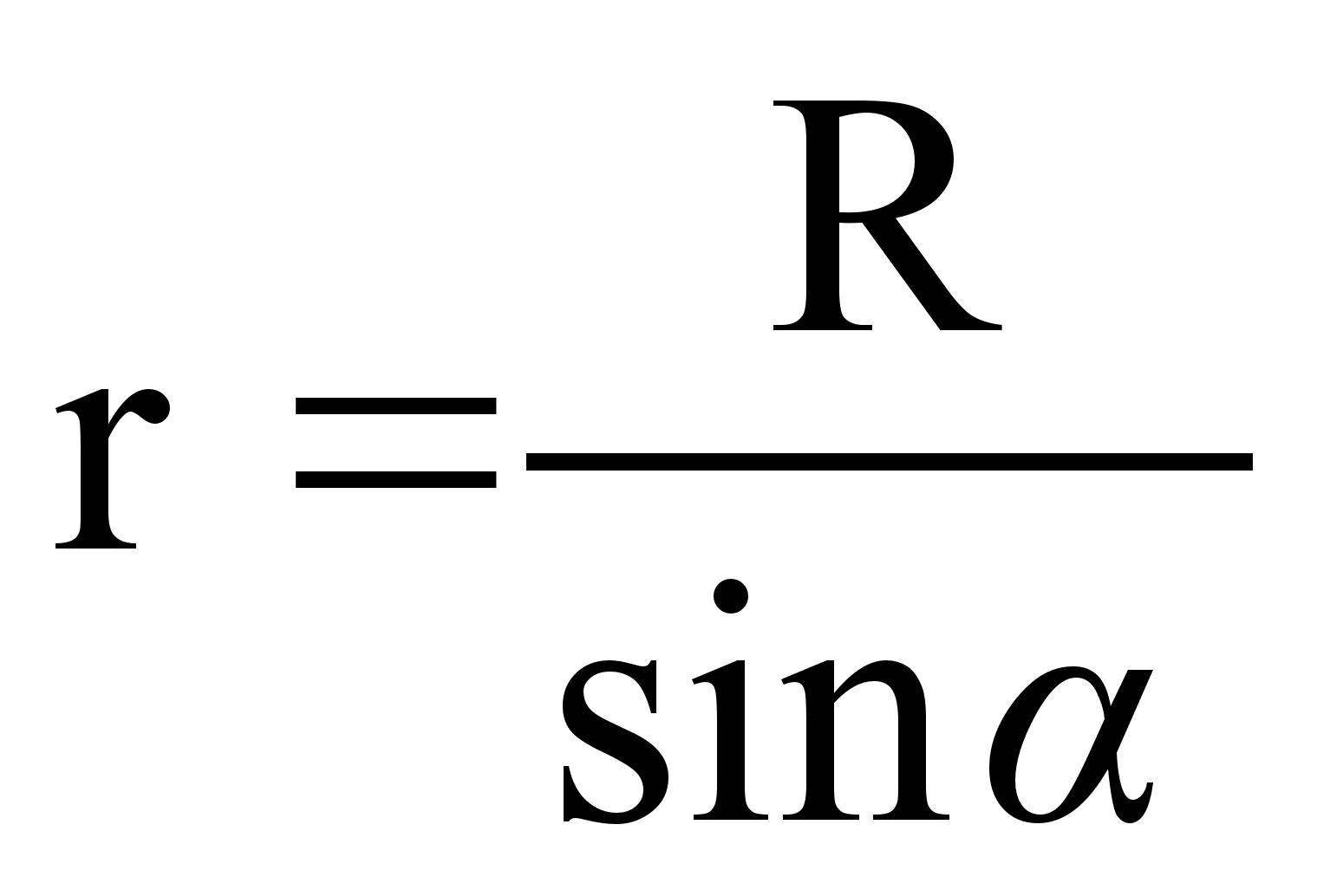 ;
; 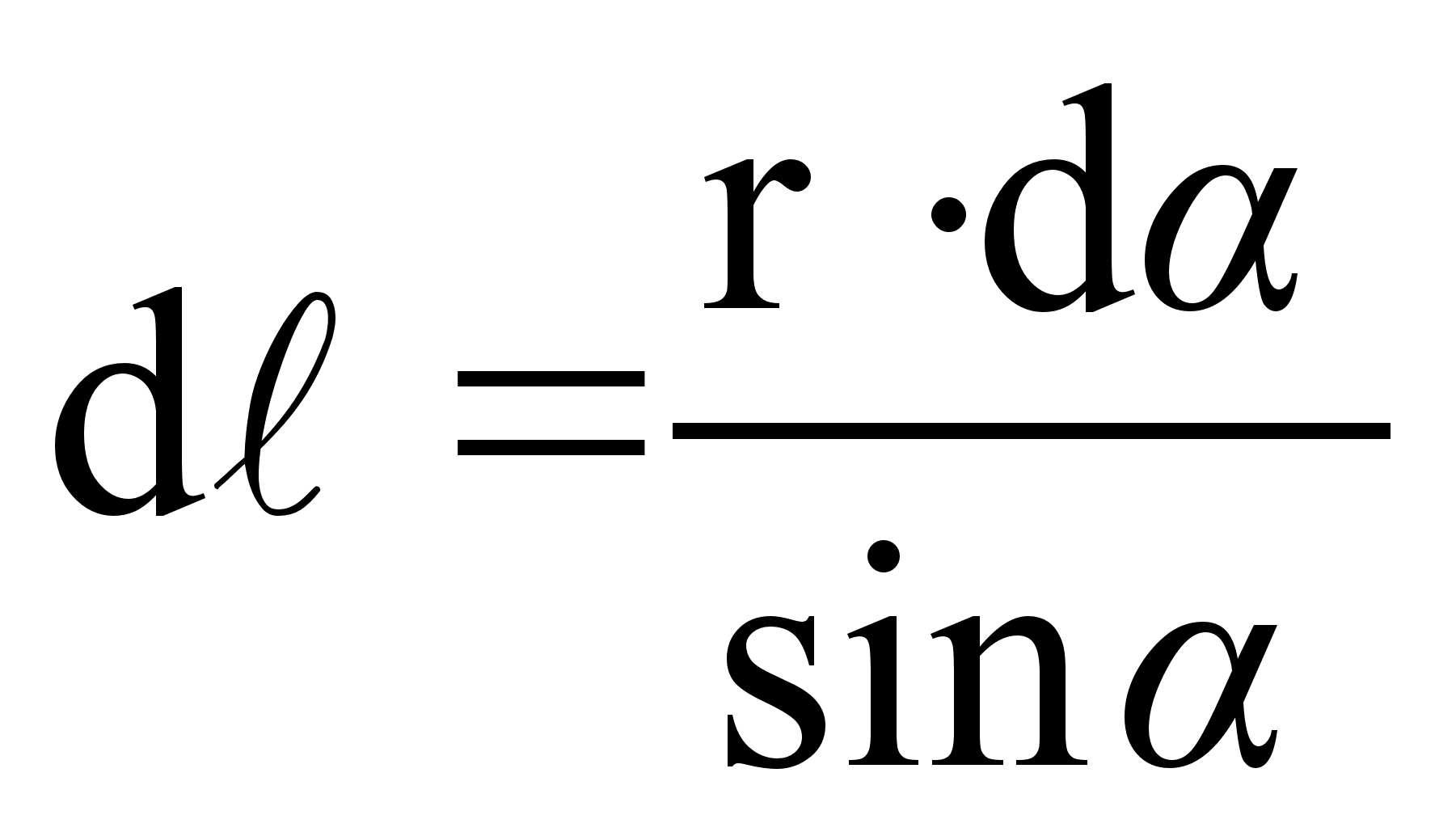 (59)
(59)
Подставим (59) в (57)
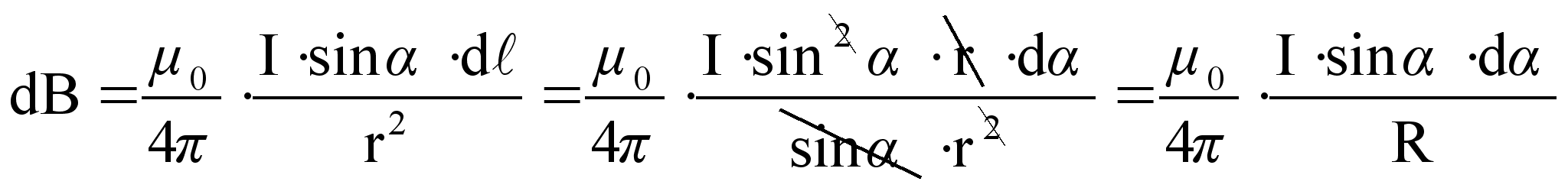
Используя (58), получим
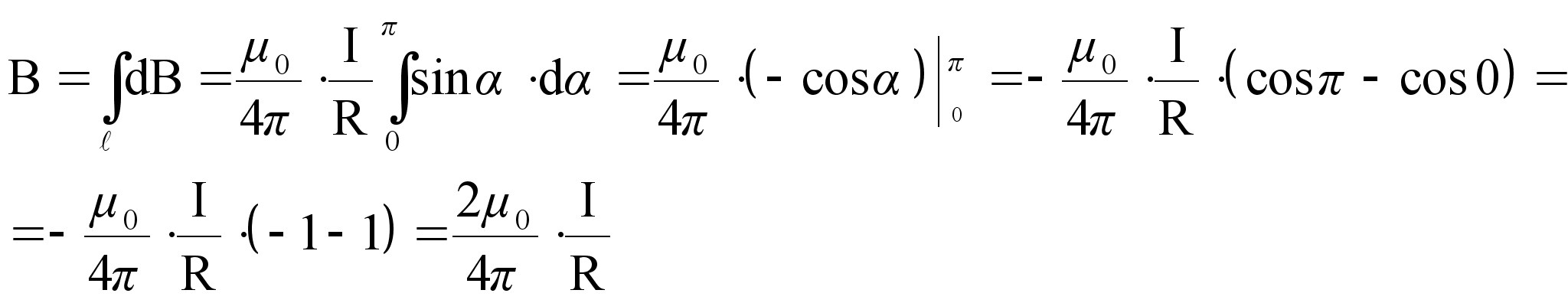
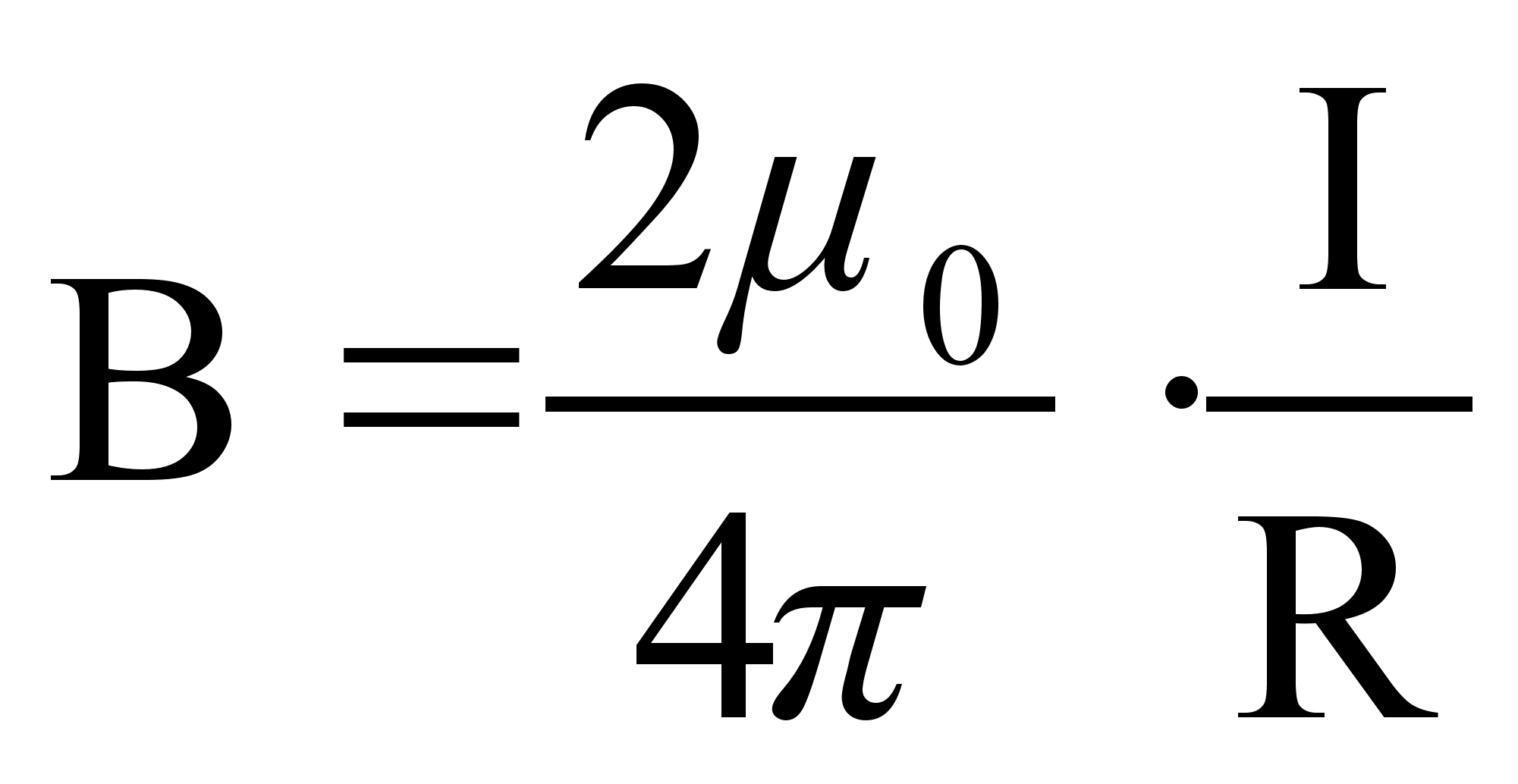 (60)
(60)
Магнитное поле в центре кругового тока.
(Рисунок)
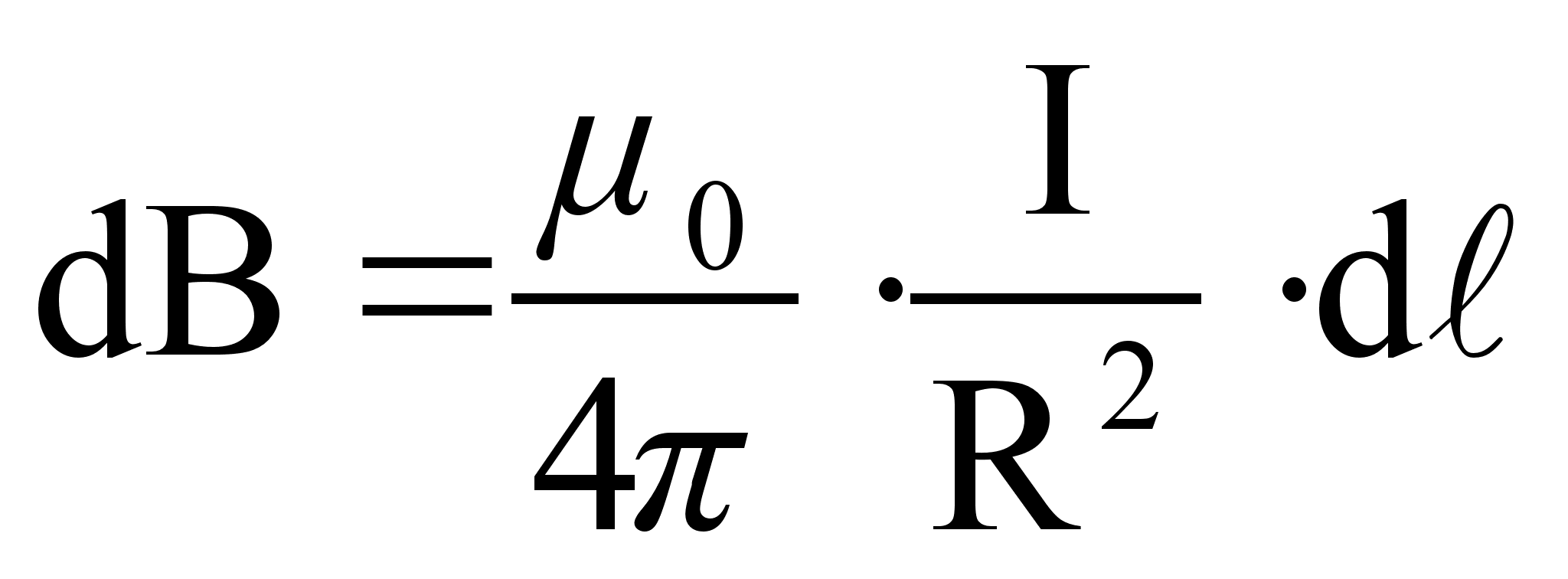
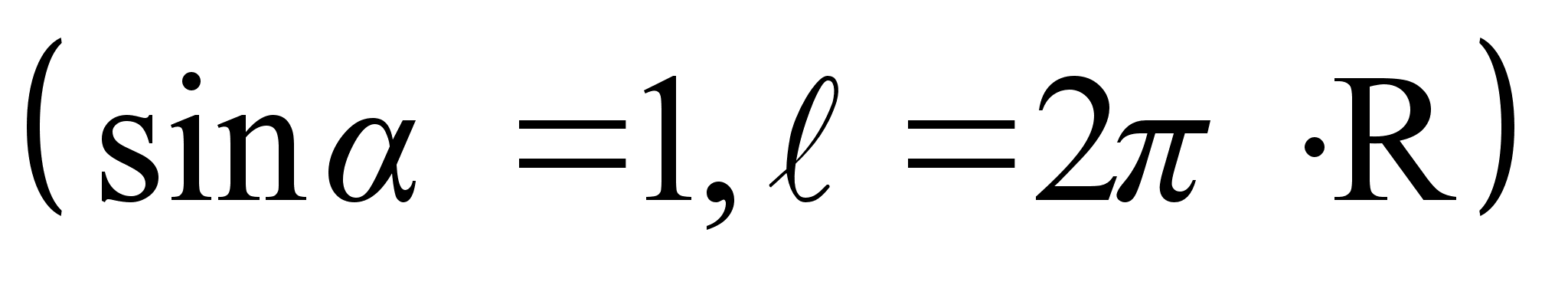
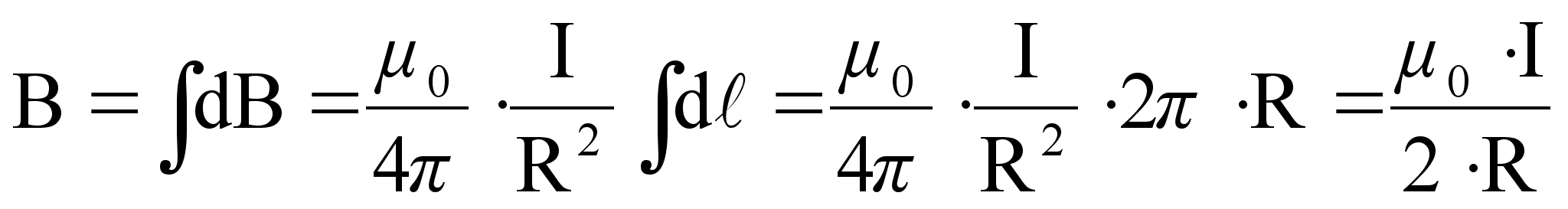
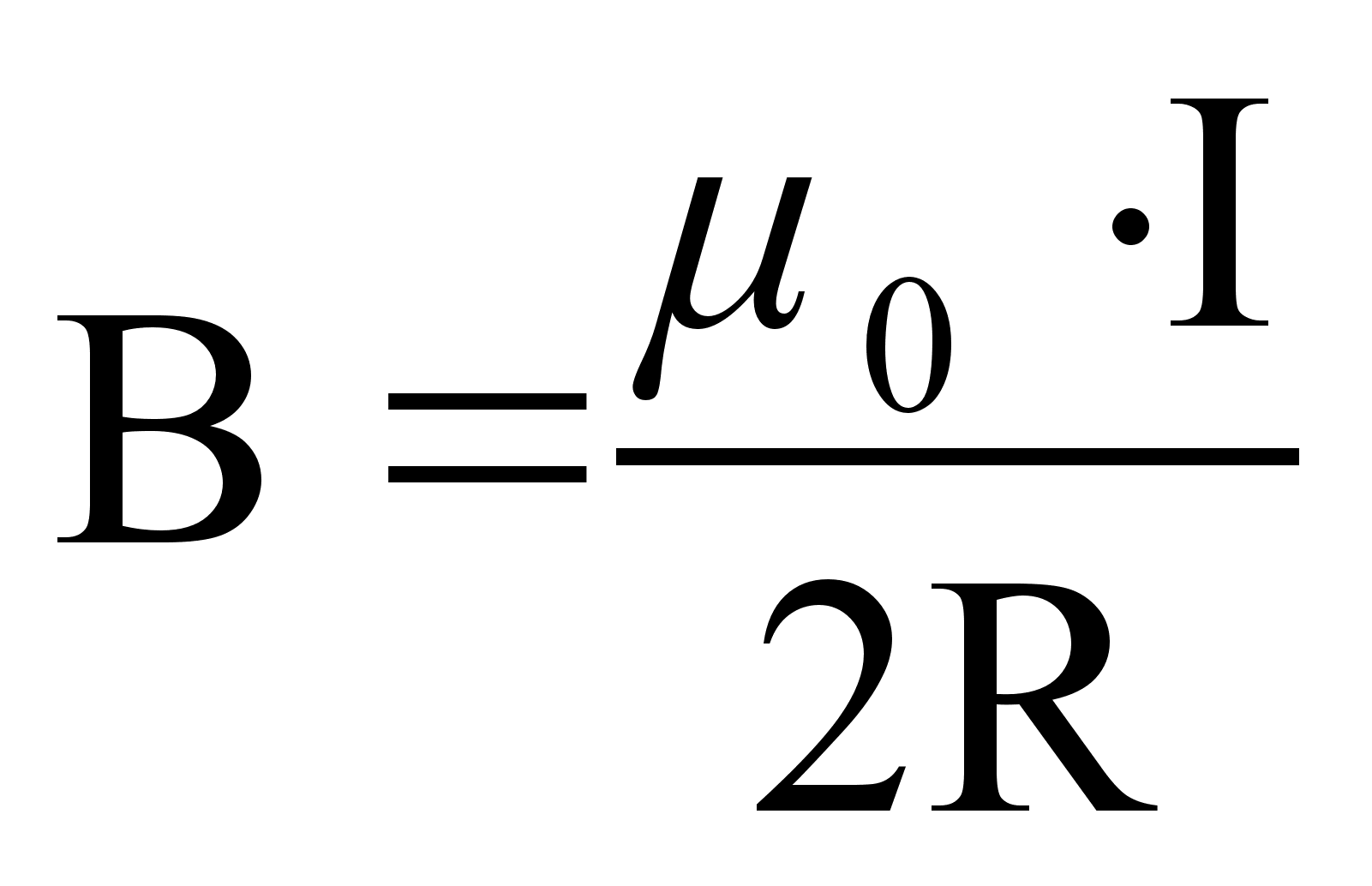 (61)
(61)
Закон Ампера.
Взаимодействие параллельных проводников.
Ампер установил, что сила , с которой магнитное поле действует на элемент проводника
, с которой магнитное поле действует на элемент проводника 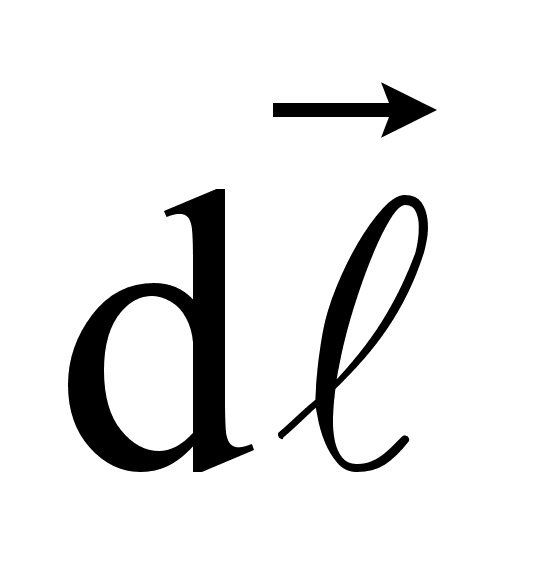 с током, находящимся в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника
с током, находящимся в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника  на вектор магнитной индукции
на вектор магнитной индукции 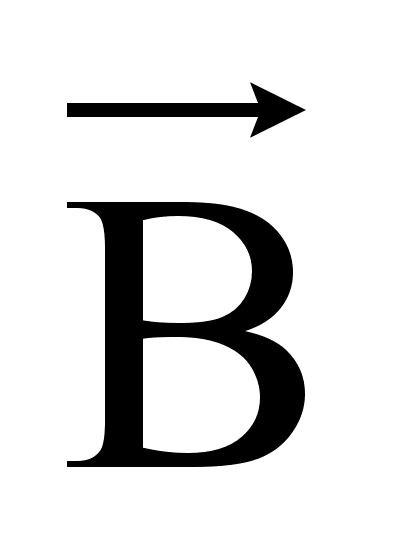 :
:
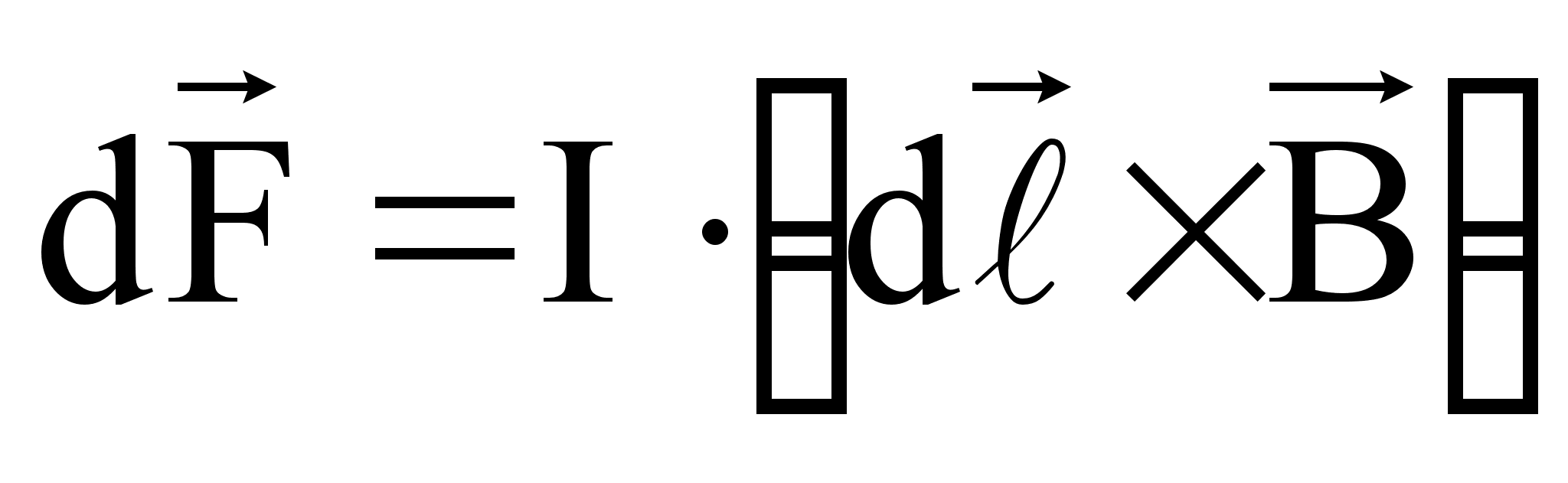 (62)
(62)
Направление силы находится по правилу левой руки:
Линии магнитной индукции входят в ладонь, четыре пальца направлены по току, отогнутый большой палец показывает направление силы Ампера.
Модуль силы Ампера определяется по формуле:
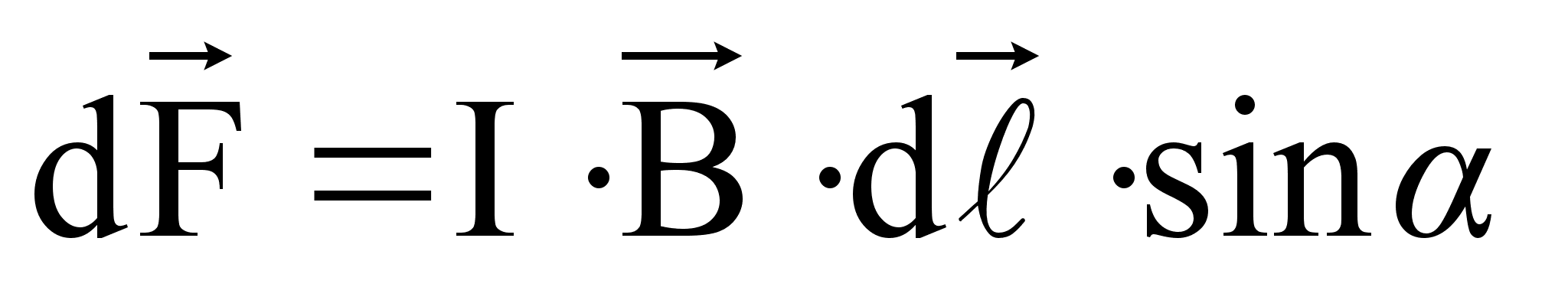
где 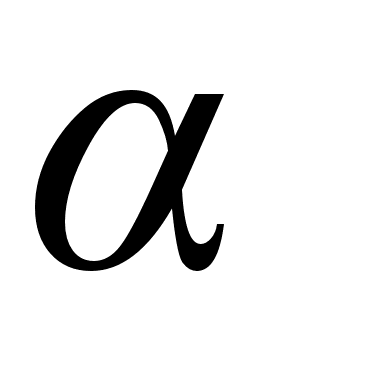 - угол между векторами
- угол между векторами 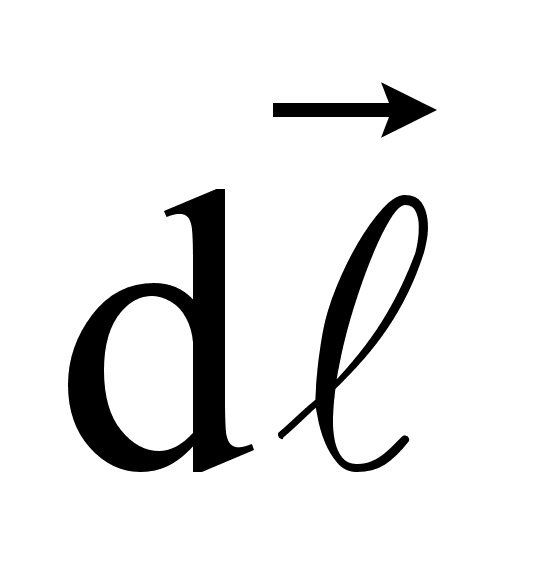 и
и 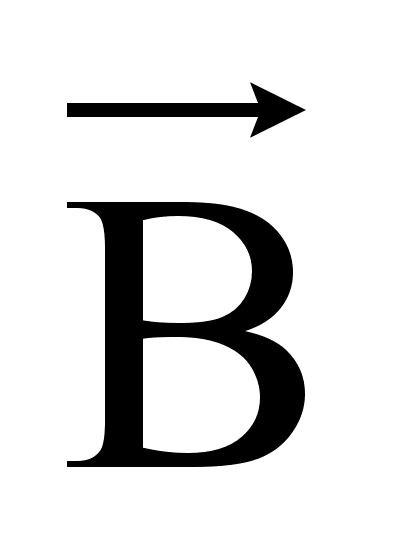 .
.
Применим закон Ампера для определения силы взаимодействия двух параллельных проводников.
???????????????7
????????????????
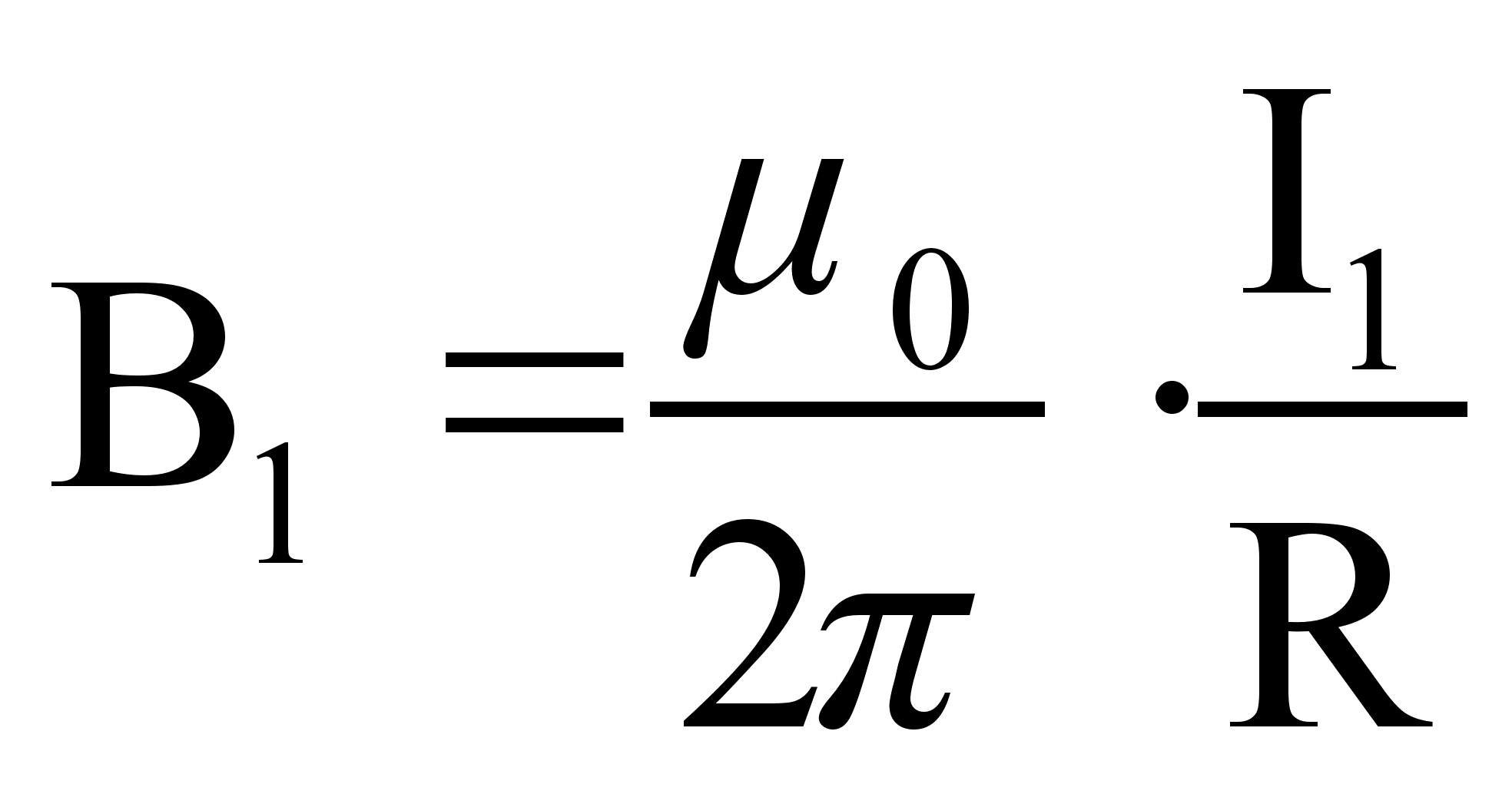 (64)
(64)
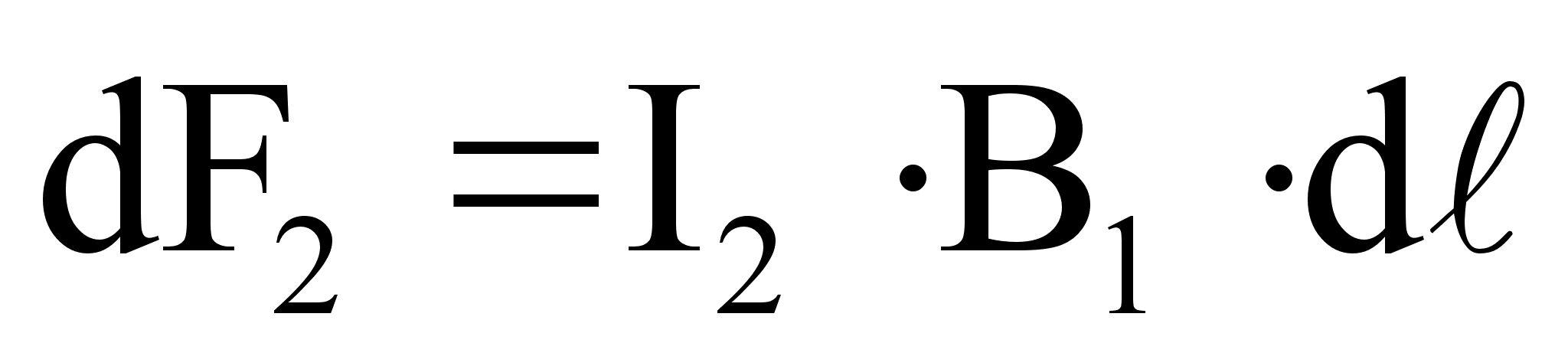 (65)
(65)
Подставляя (64) в (65), получим:
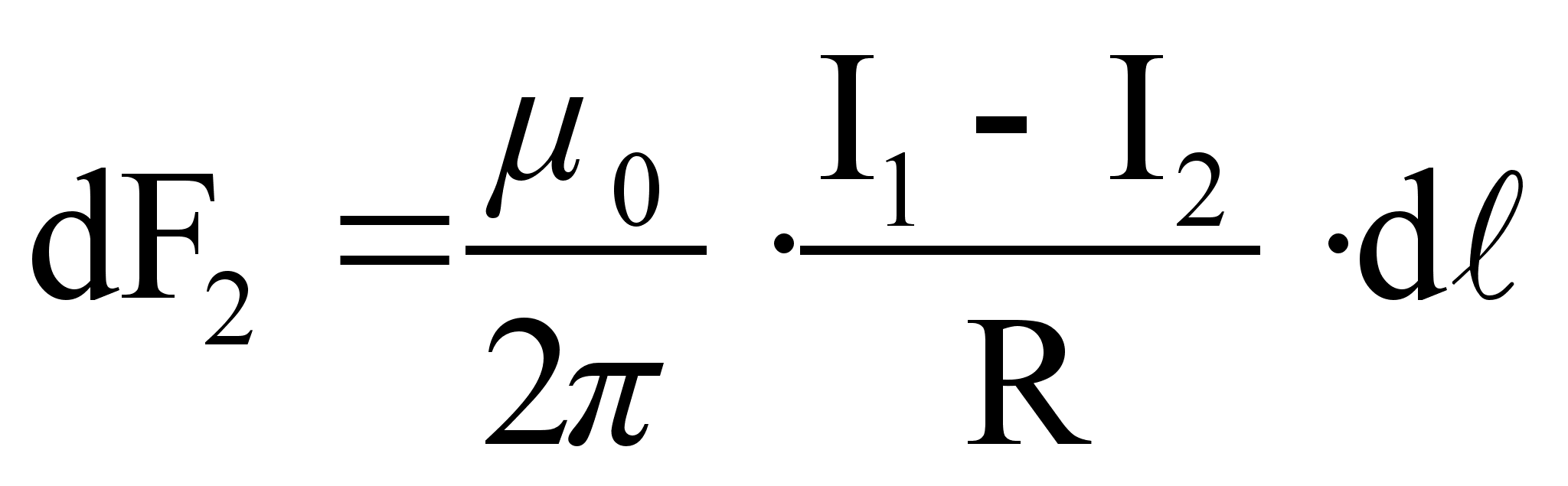 (66)
(66)
Рассуждая аналогично, получим
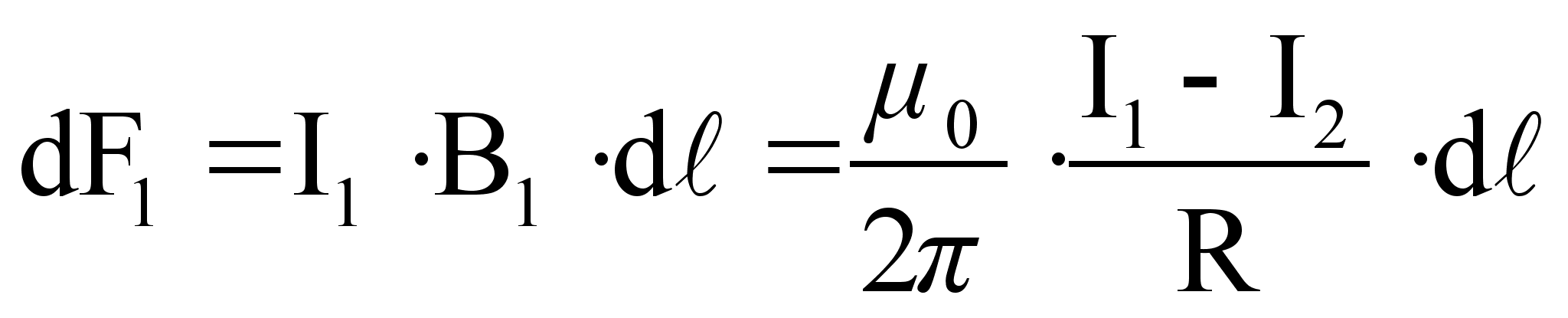 (67)
(67)
Сравнивая (66) и (67), видим, что

То есть два проводника притягиваются друг к другу с силой
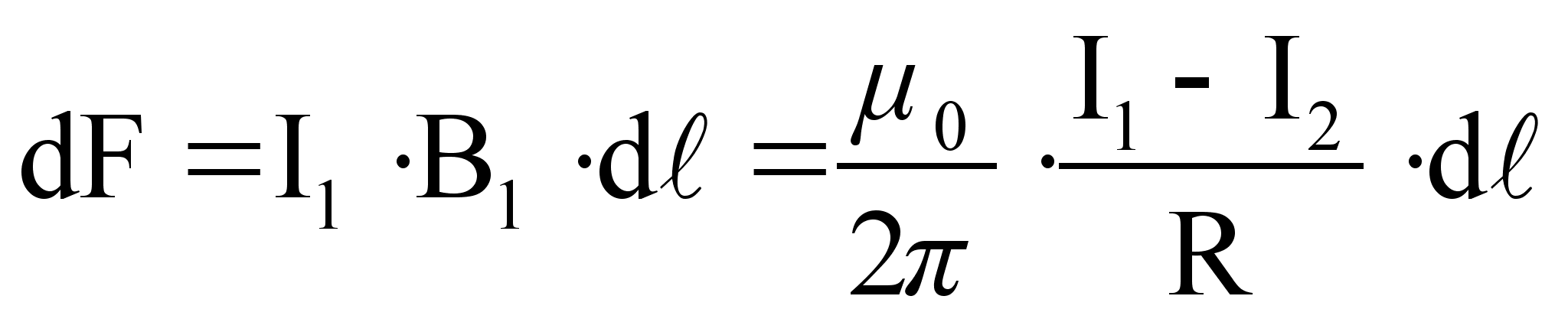 (68)
(68)
Если токи идут в противоположных направлениях, то проводники отталкиваются.
Относительность магнитных и электрических полей.
Когда ранее говорилось, что магнитная сила, действующая на заряд пропорциональна скорости, возникал вопрос: по отношению к какой системе отсчёта. Оказывается, что годится любая инерциальная система отсчёта.
Изучение электричества и магнетизма привело Эйнштейна к открытию принципа относительности.
Уравнения, выражающие законы природы, инвариантны по отношению к преобразующим координат и времени от одной системы отсчёта к другой.
Применим принцип относительности к магнетизму:
(Рисунки)
В системе К покоится проволока с током I. В системе 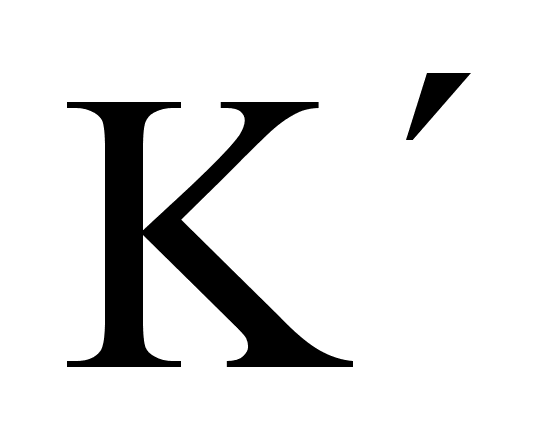 покоится заряд и движущаяся проволока с током
покоится заряд и движущаяся проволока с током 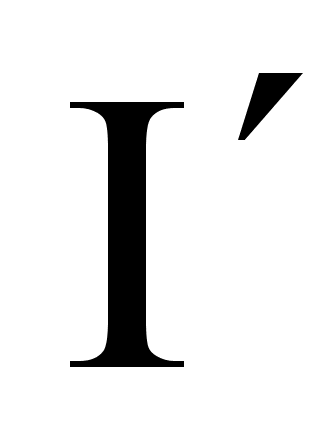 .
.
Рассмотрим первый случай: сумма зарядов в проволоке равна нулю, то есть проволока не заряжена и электрическое поле вне её отсутствует. Поэтому на частицу с зарядом –q действует сила:

Выражаем 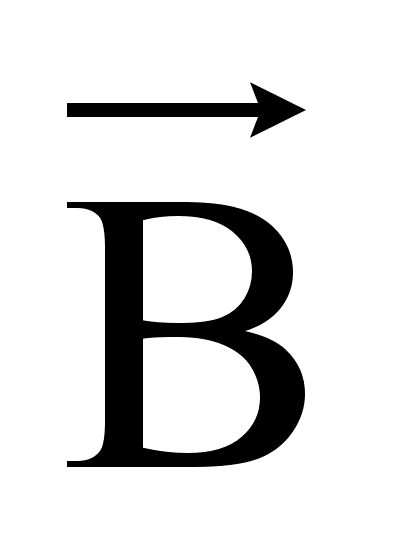 из закона Био-Савара-Лапласа:
из закона Био-Савара-Лапласа:
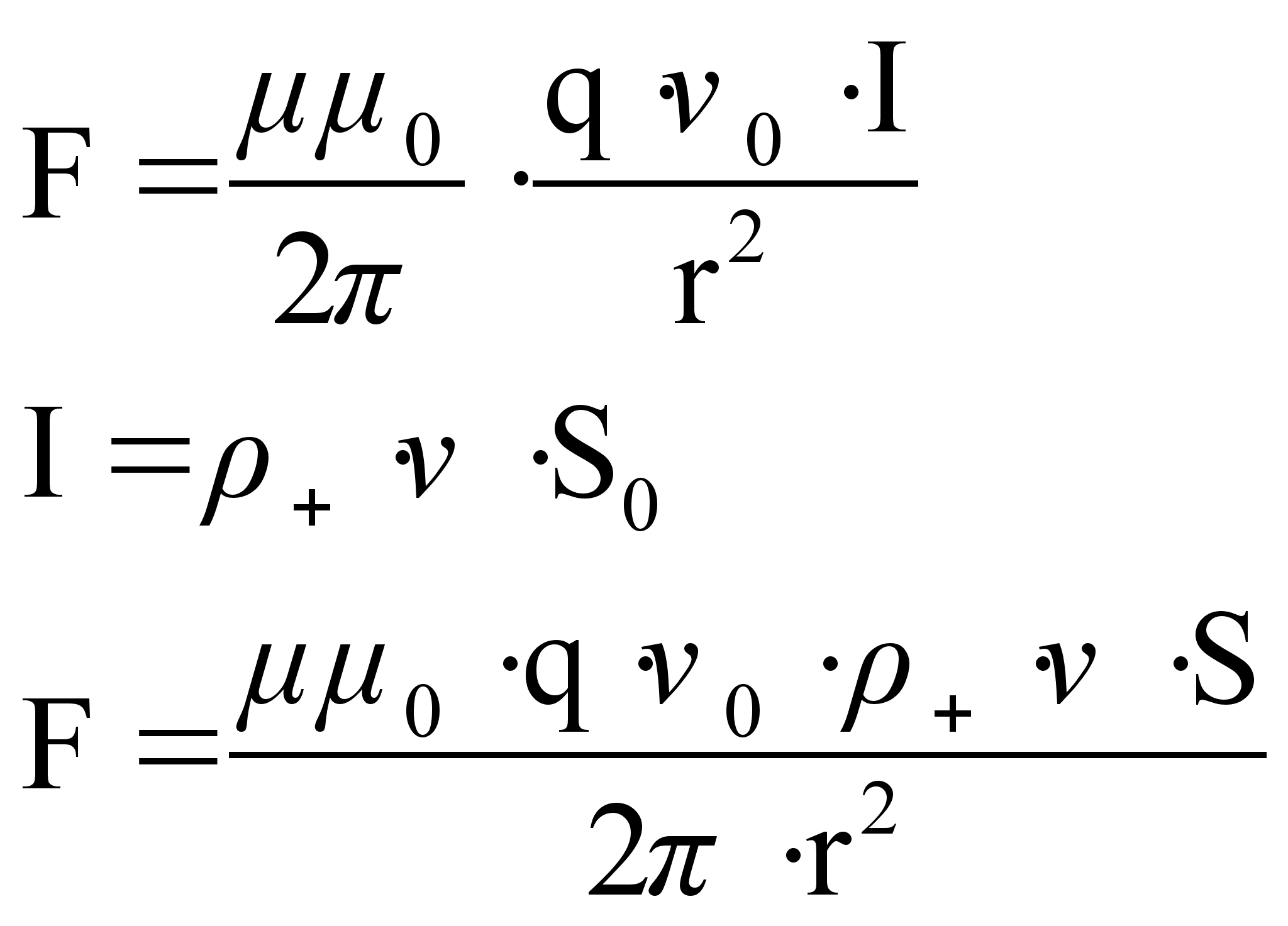
Рассмотрим частный случай, когда 
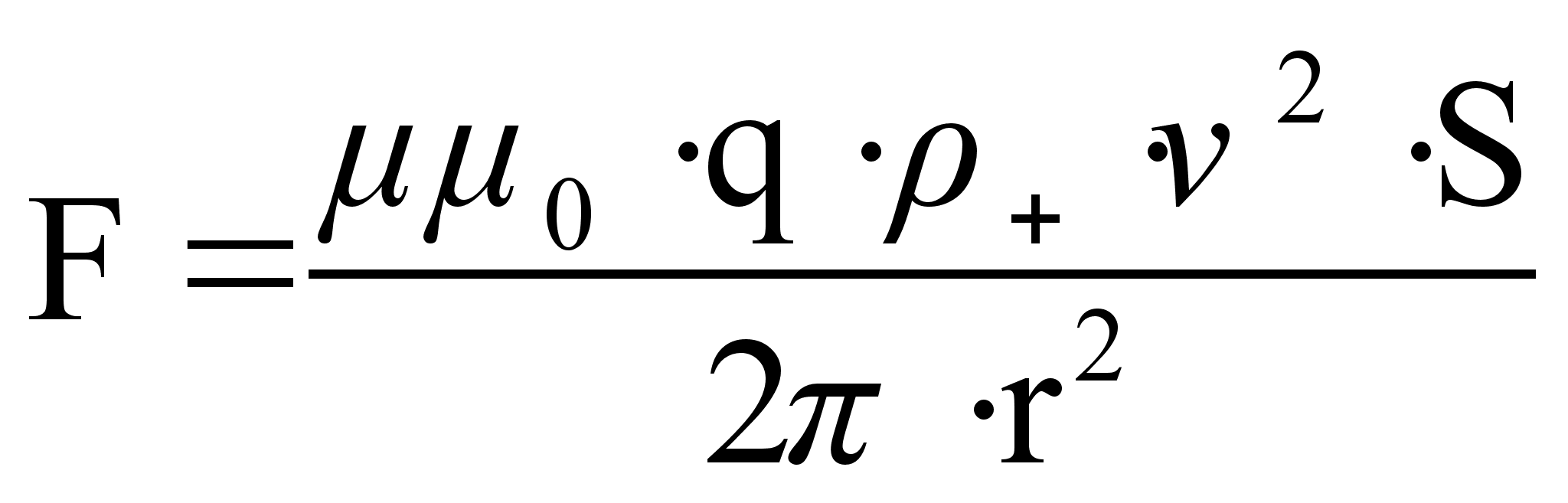 (76)
(76)
Второй случай: движущиеся положительные заряды (ионы кристаллической решётки, проволоки) создают магнитное поле, но так как ??????????????? в системе отсчёта 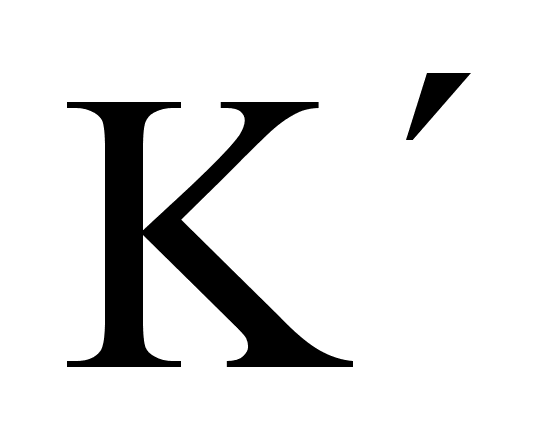 покоится ????????7
покоится ????????7
Если и возникает магнитная сила, то это сила со стороны электрического поля. Следовательно, движущаяся нейтральная проволока с током становится заряженной.
Вычислим плотность заряда в проволоке в системе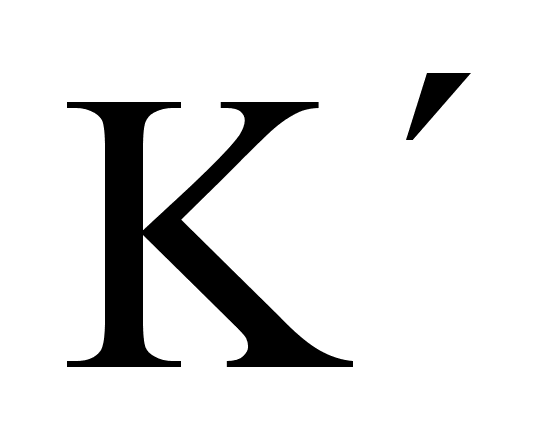 , пользуясь тем, что мы уже знаем о ней в системе К.
, пользуясь тем, что мы уже знаем о ней в системе К.
Казалось бы, плотность одинакова, но из специальной теории относительности известно, что при переходе от одной системы отсчёта к другой, длины меняются, следовательно, меняются и объёмы.
В проволоке с  и с
и с 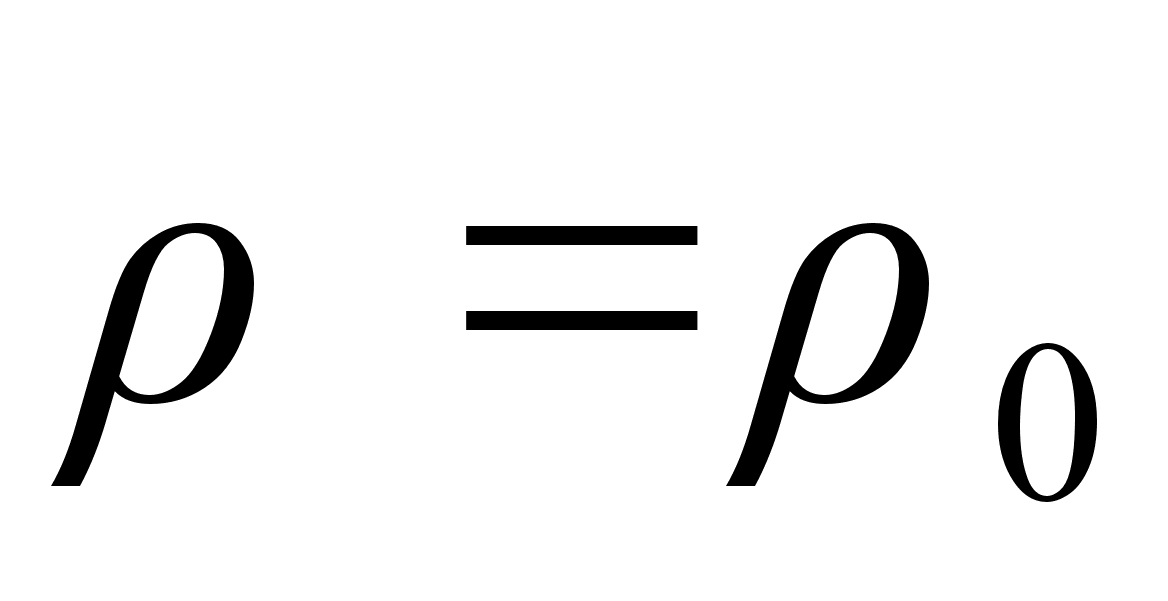 создаётся полный заряд
создаётся полный заряд
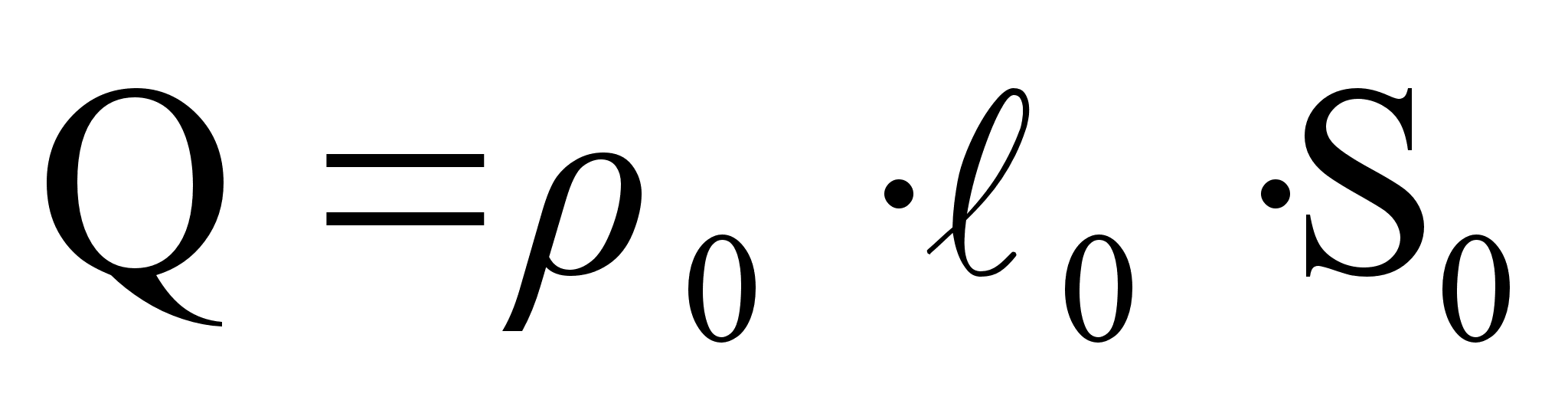
Если эти заряды будут двигаться со скоростью  , то они будут находиться в объёме меньшей длины:
, то они будут находиться в объёме меньшей длины:
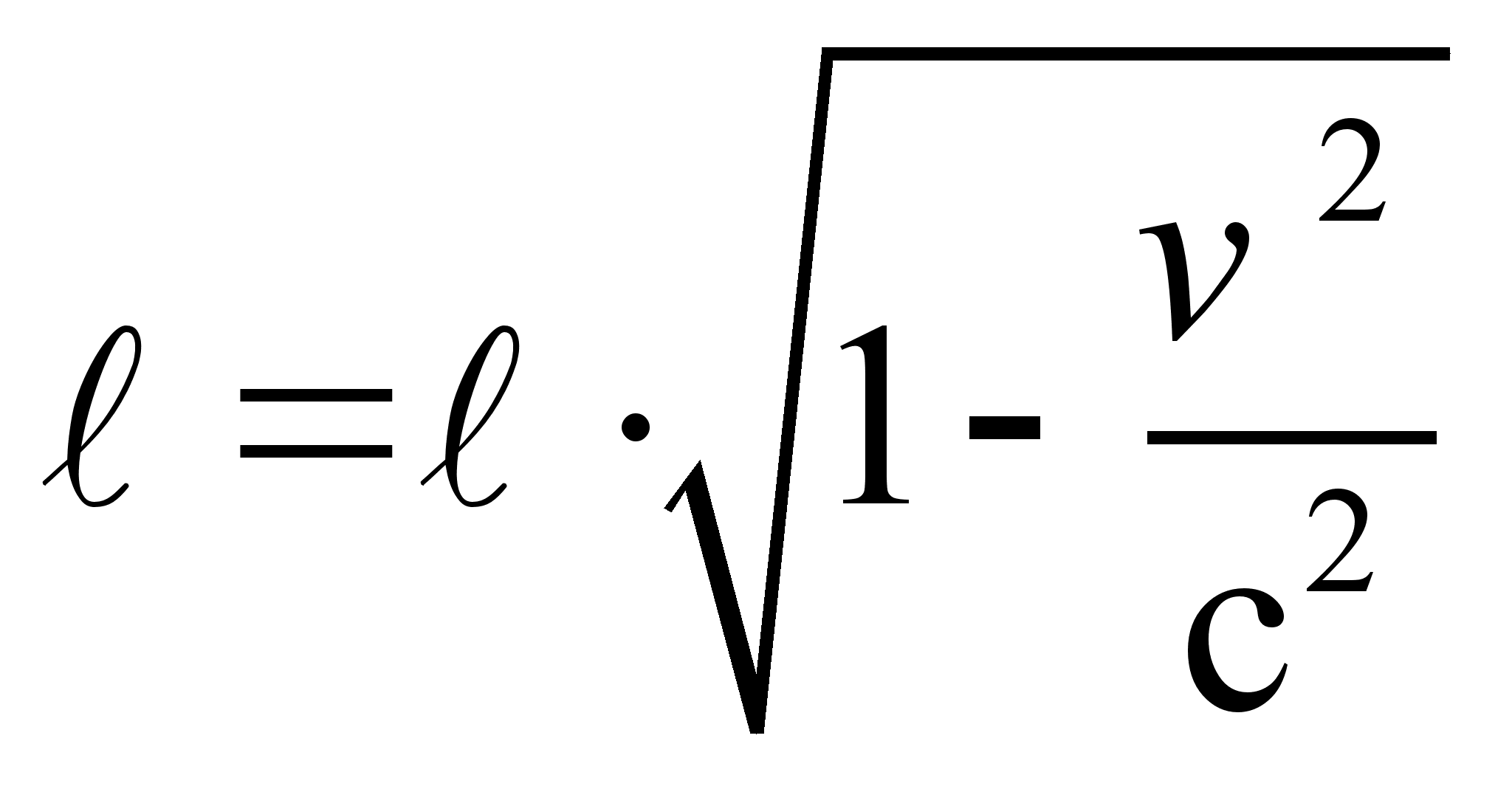
(Рисунок)
Полный заряд в системе 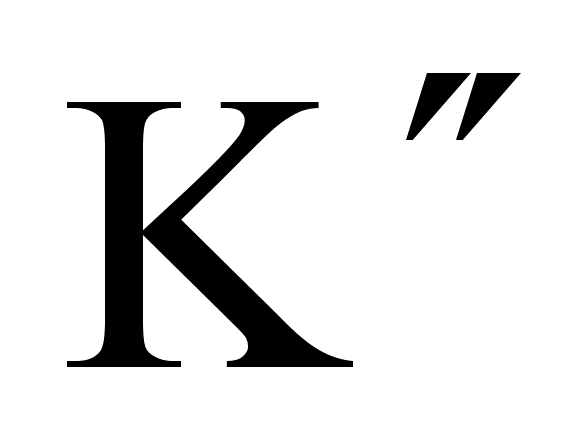 будет равен
будет равен
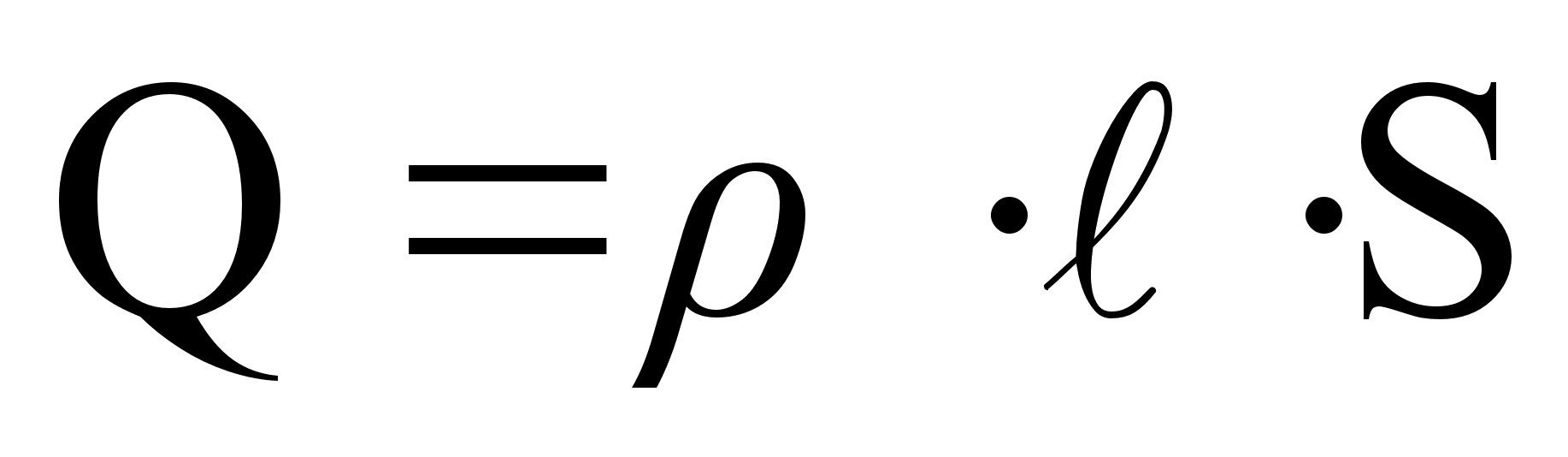 ,
,
где 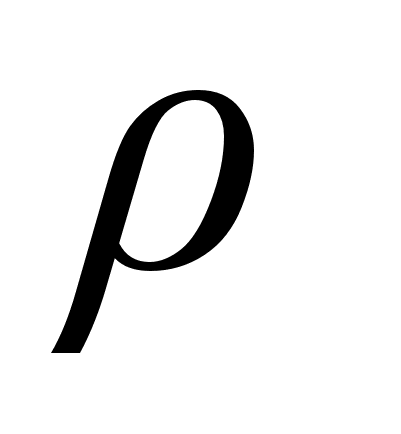 - плотность заряда в движущейся системе.
- плотность заряда в движущейся системе.
Из закона сохранения заряда:
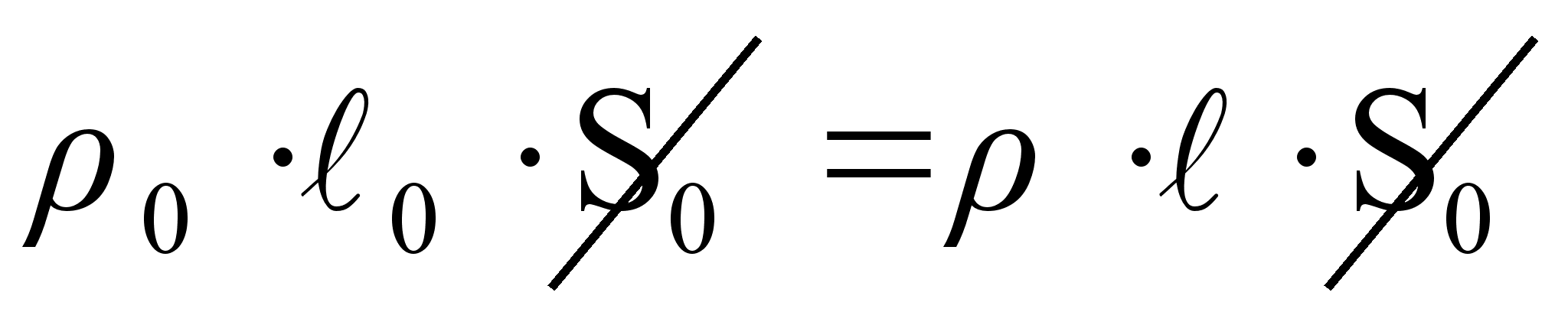
или  , откуда
, откуда 
То есть движущиеся совокупности зарядов сменяются тем же образом, как и релятивистская масса частицы.
Применим этот результат для плотности положительных зарядов
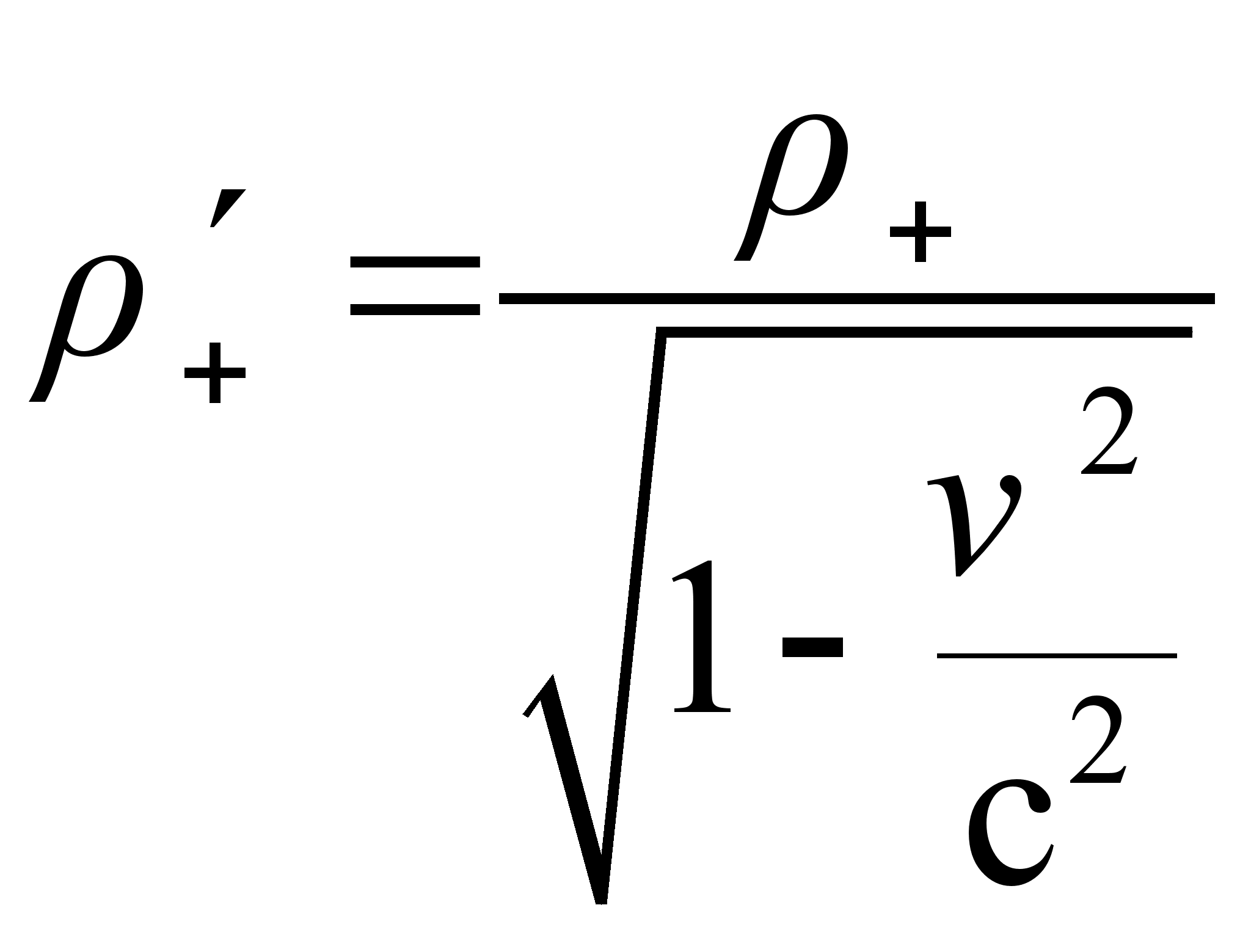
Отрицательные заряды в системе 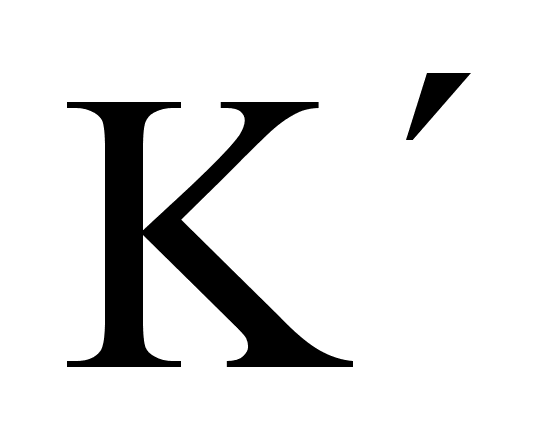 покоятся, поэтому их плотность остаётся
покоятся, поэтому их плотность остаётся 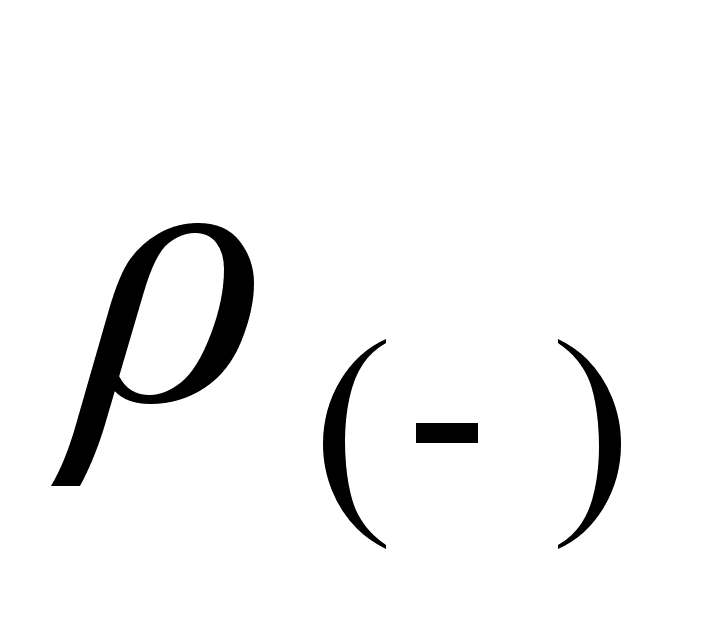 ; в системе К плотность отрицательных зарядов, движущихся со скоростью
; в системе К плотность отрицательных зарядов, движущихся со скоростью  будет равна:
будет равна:
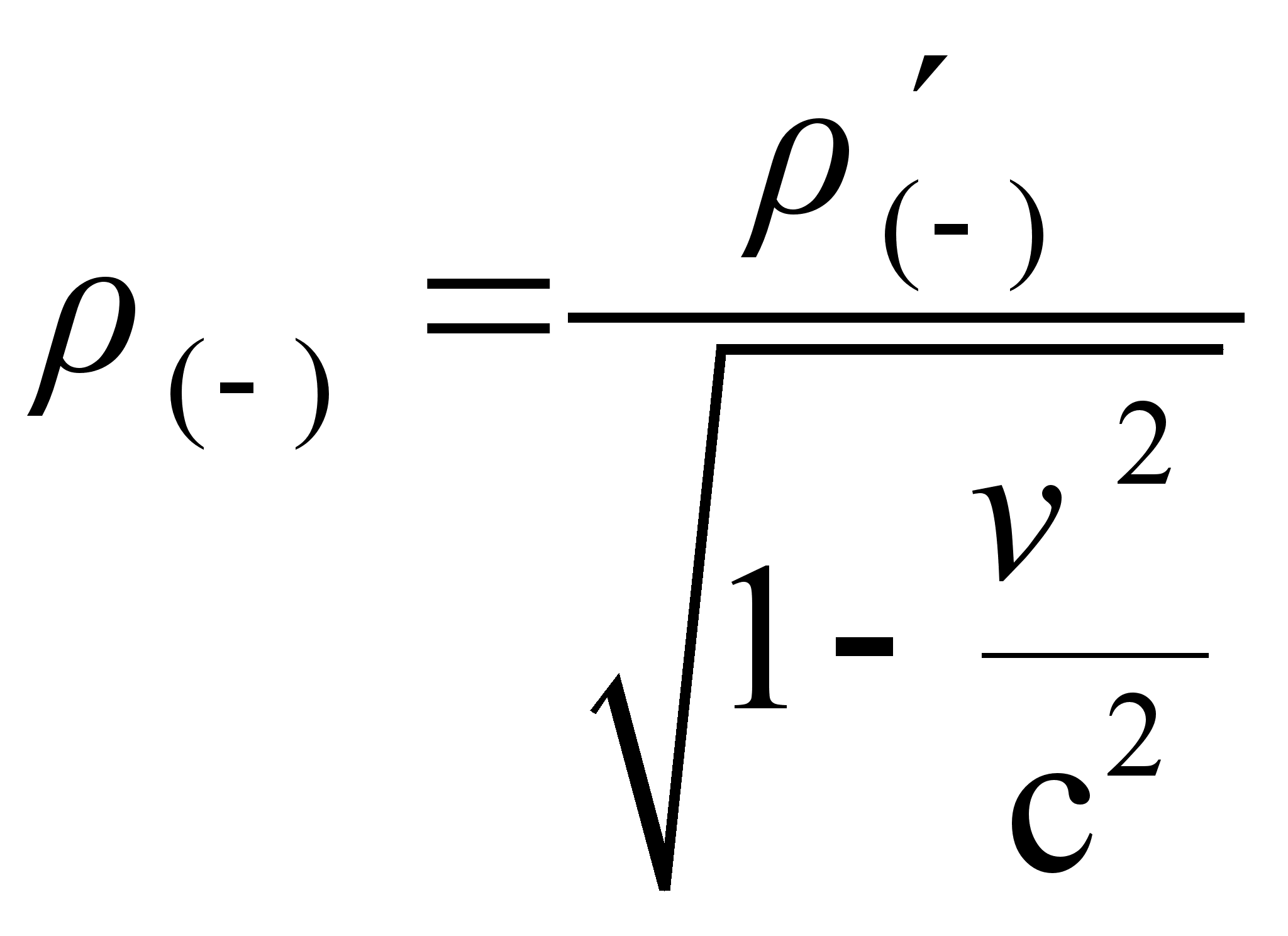 , откуда
, откуда 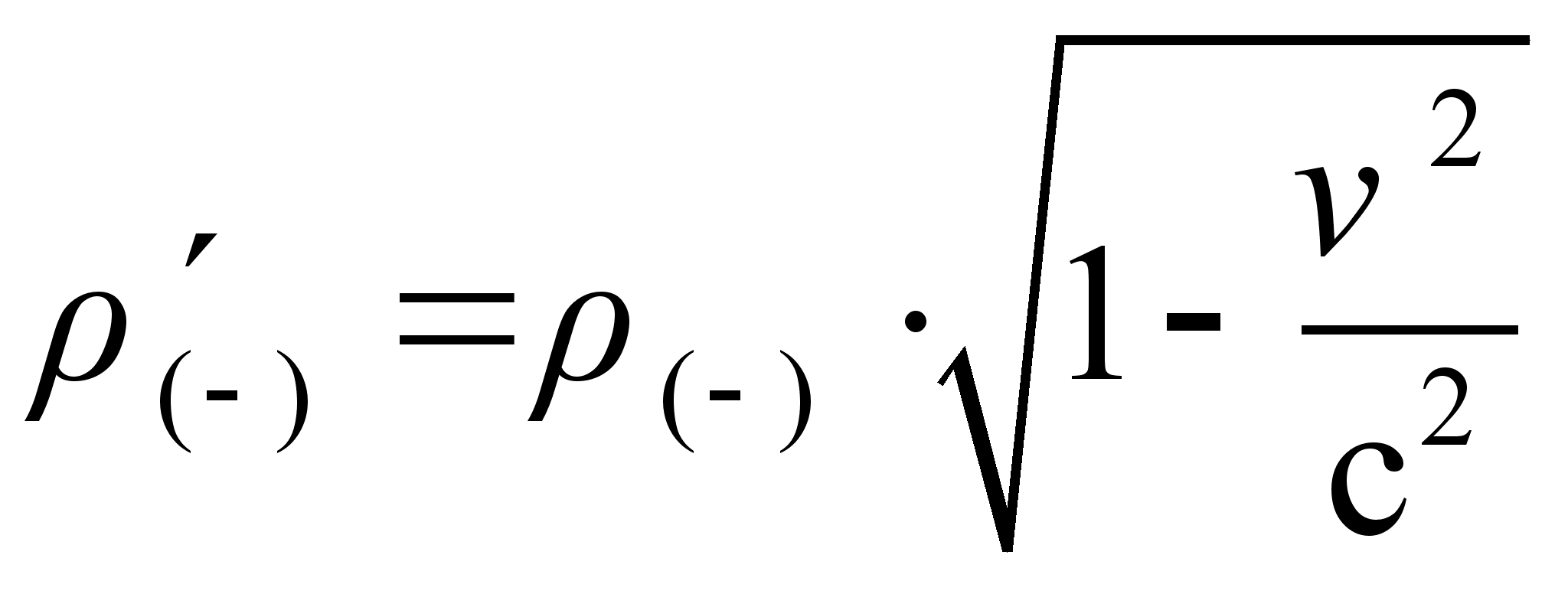
Результирующая плотность зарядов в проволоке в системе отсчёта 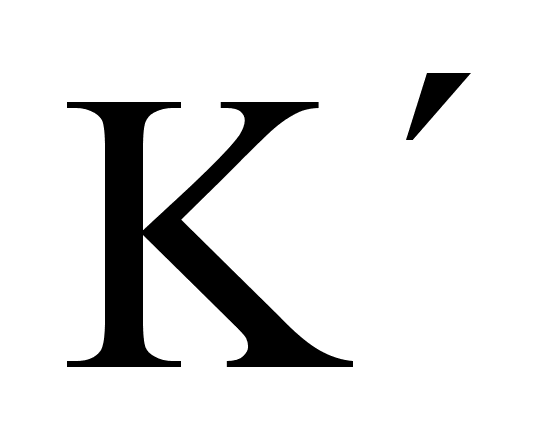 будет равна:
будет равна:
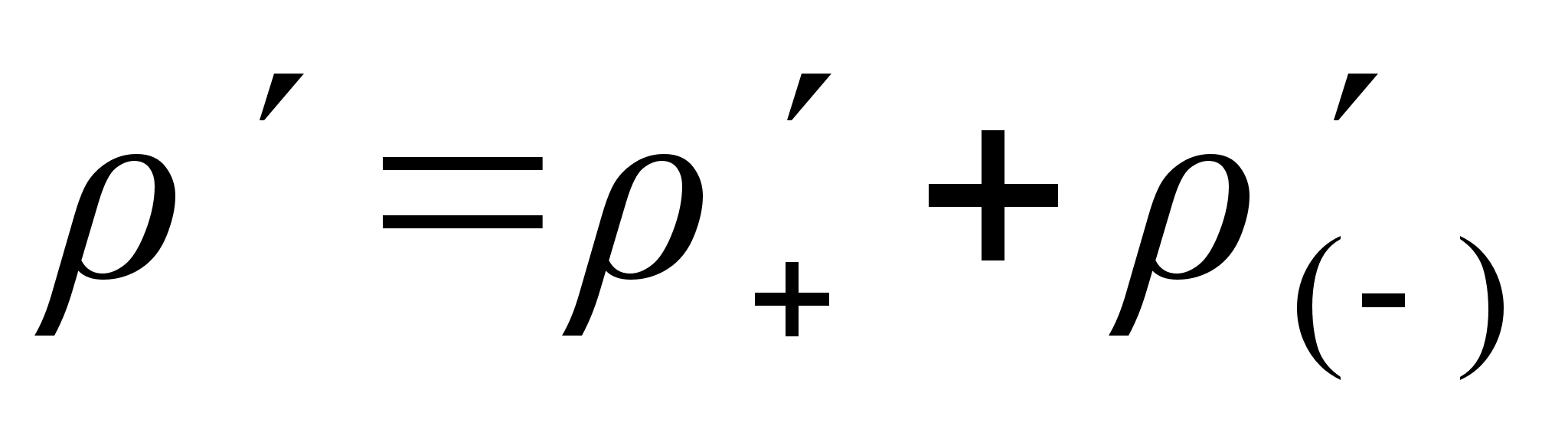
или 
Так как покоящийся проводник нейтрален, то 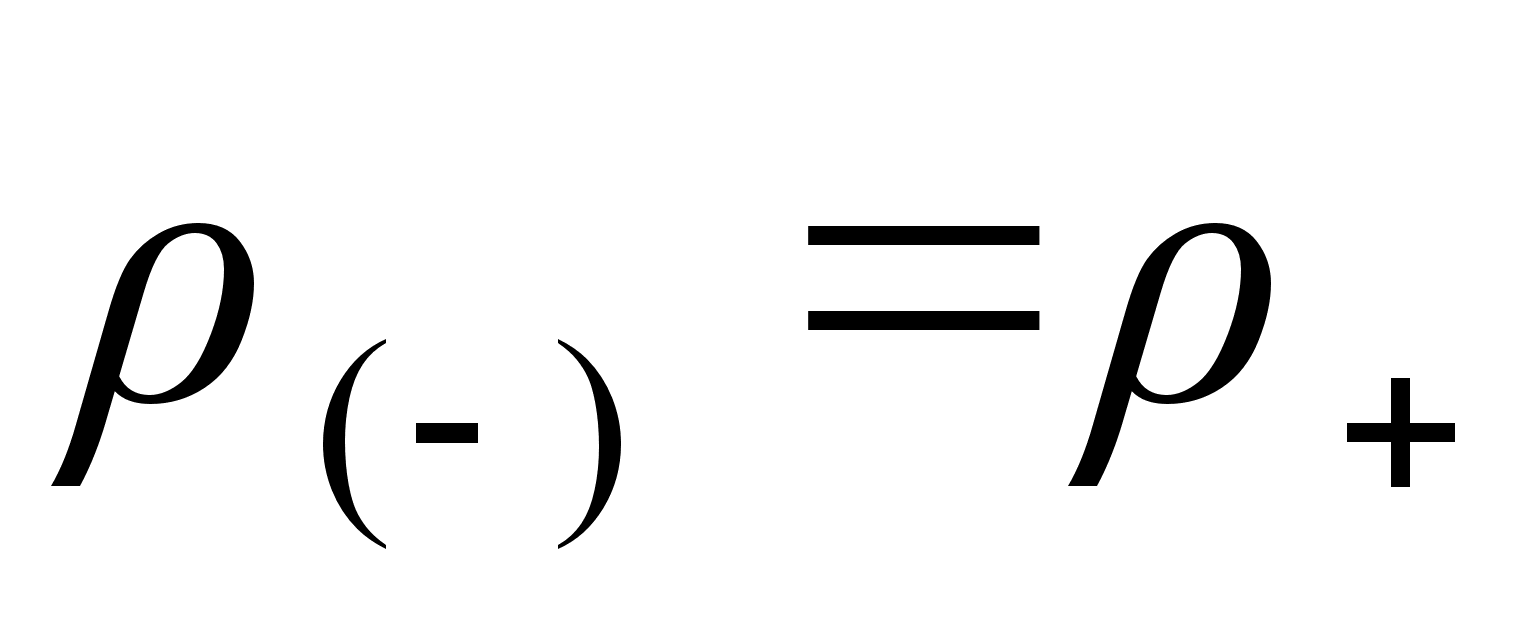 , значит
, значит
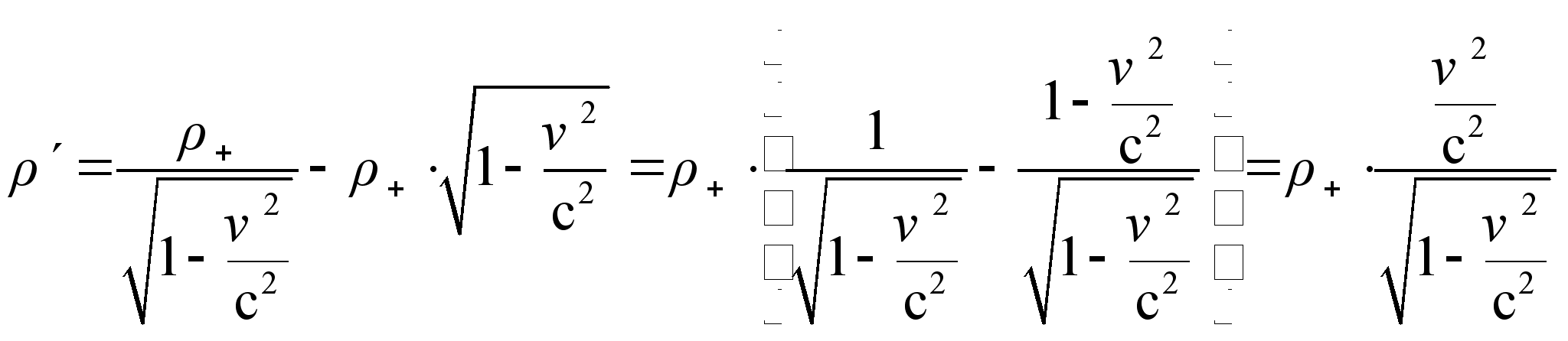
Движущаяся проволока с током будет заряжена и, следовательно, будет создавать электрическое поле:
(Рисунок)
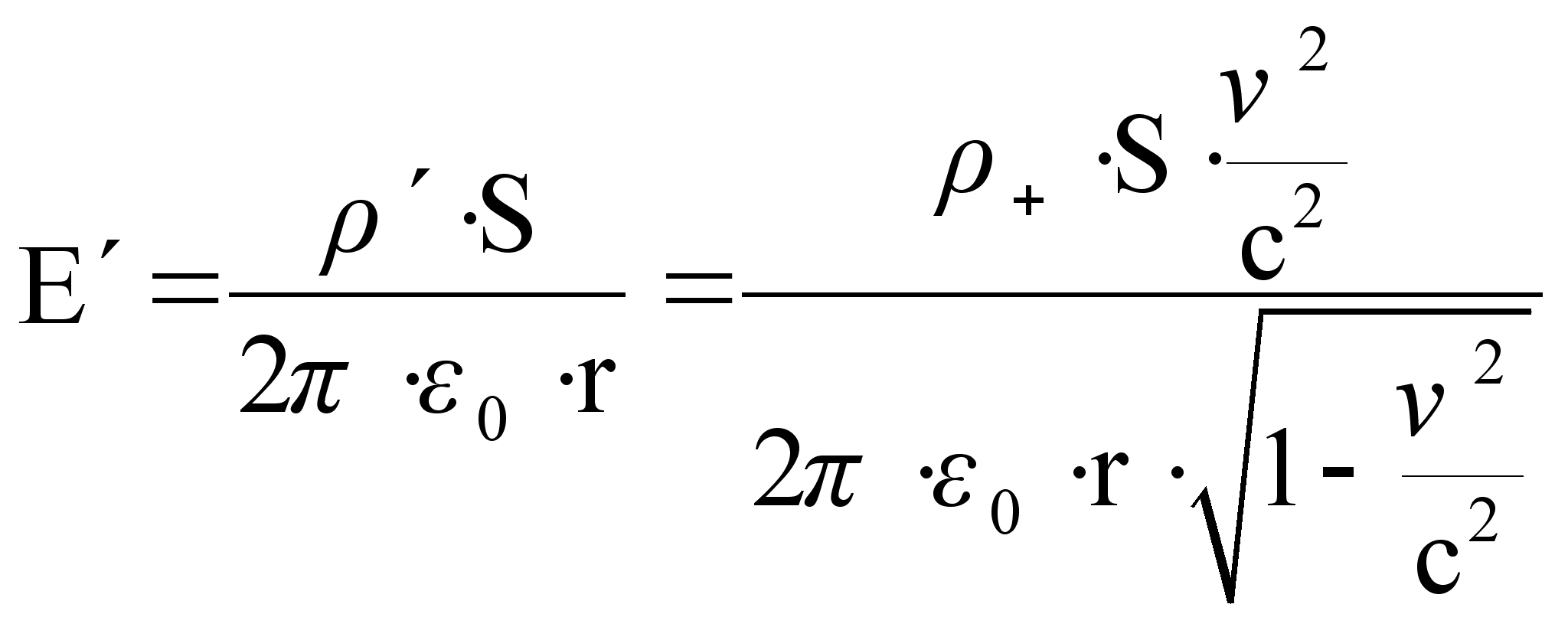
Направление сил в системах отсчёта К и 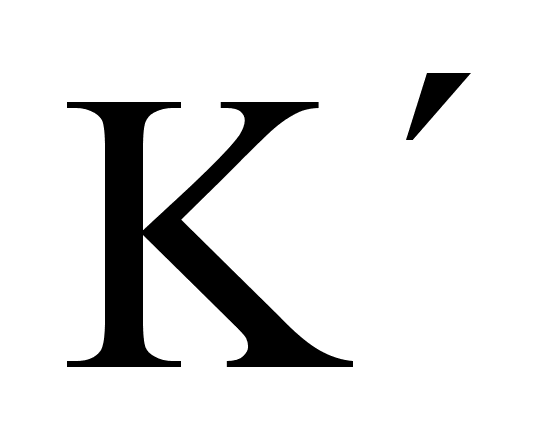 совпадает, величина силы в
совпадает, величина силы в 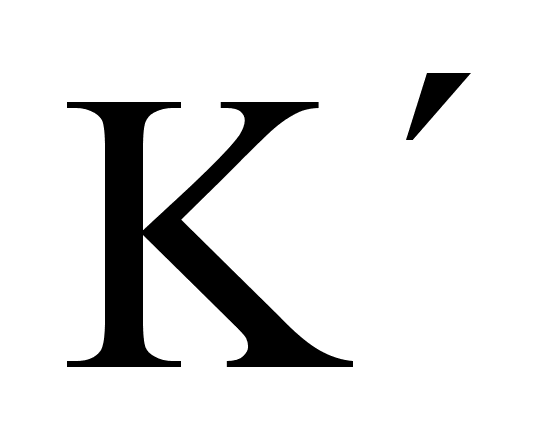 с учётом формулы (76):
с учётом формулы (76):
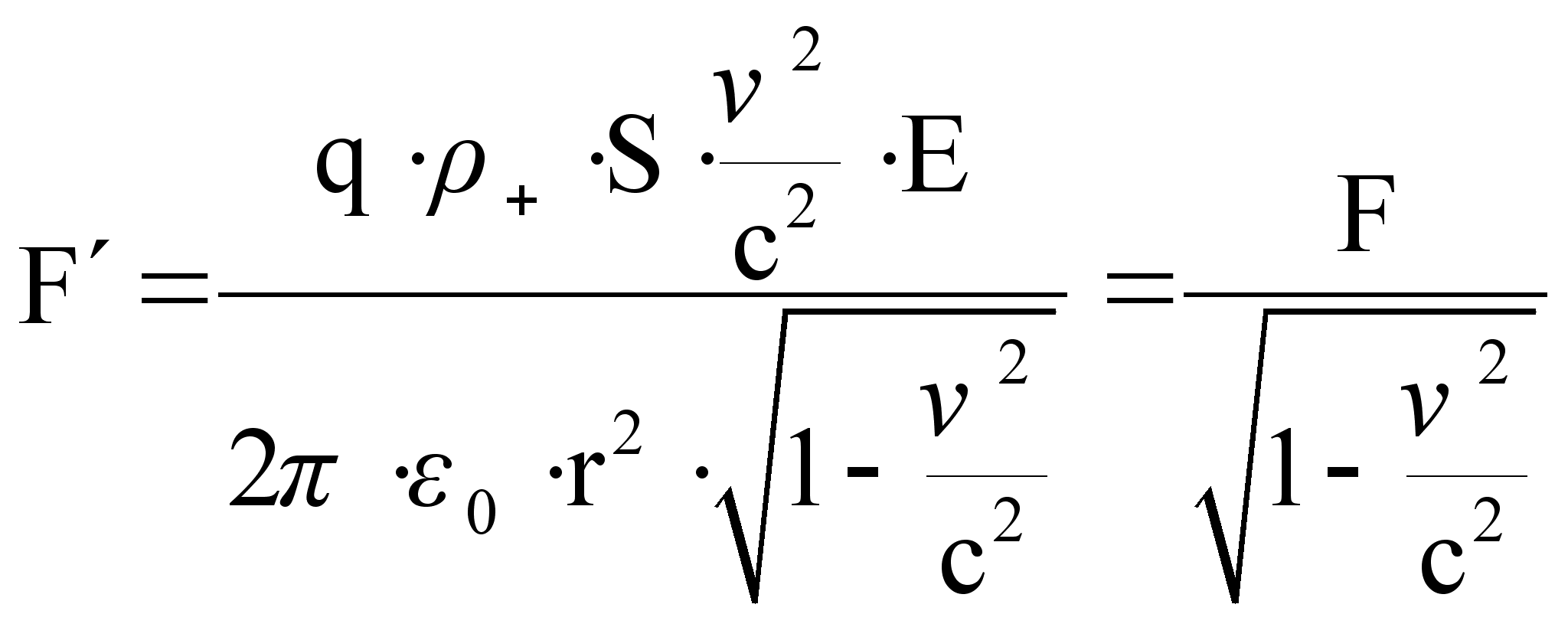 (77)
(77)
здесь учтено, что  .
.
Силы F и 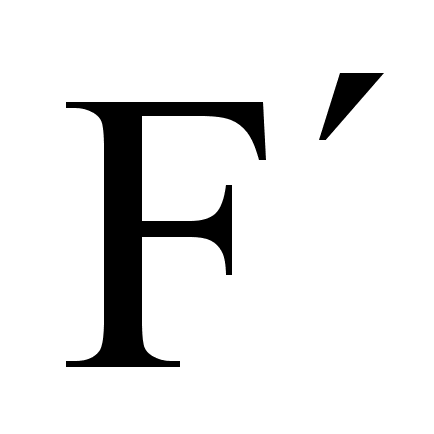 отличаются только множителем
отличаются только множителем 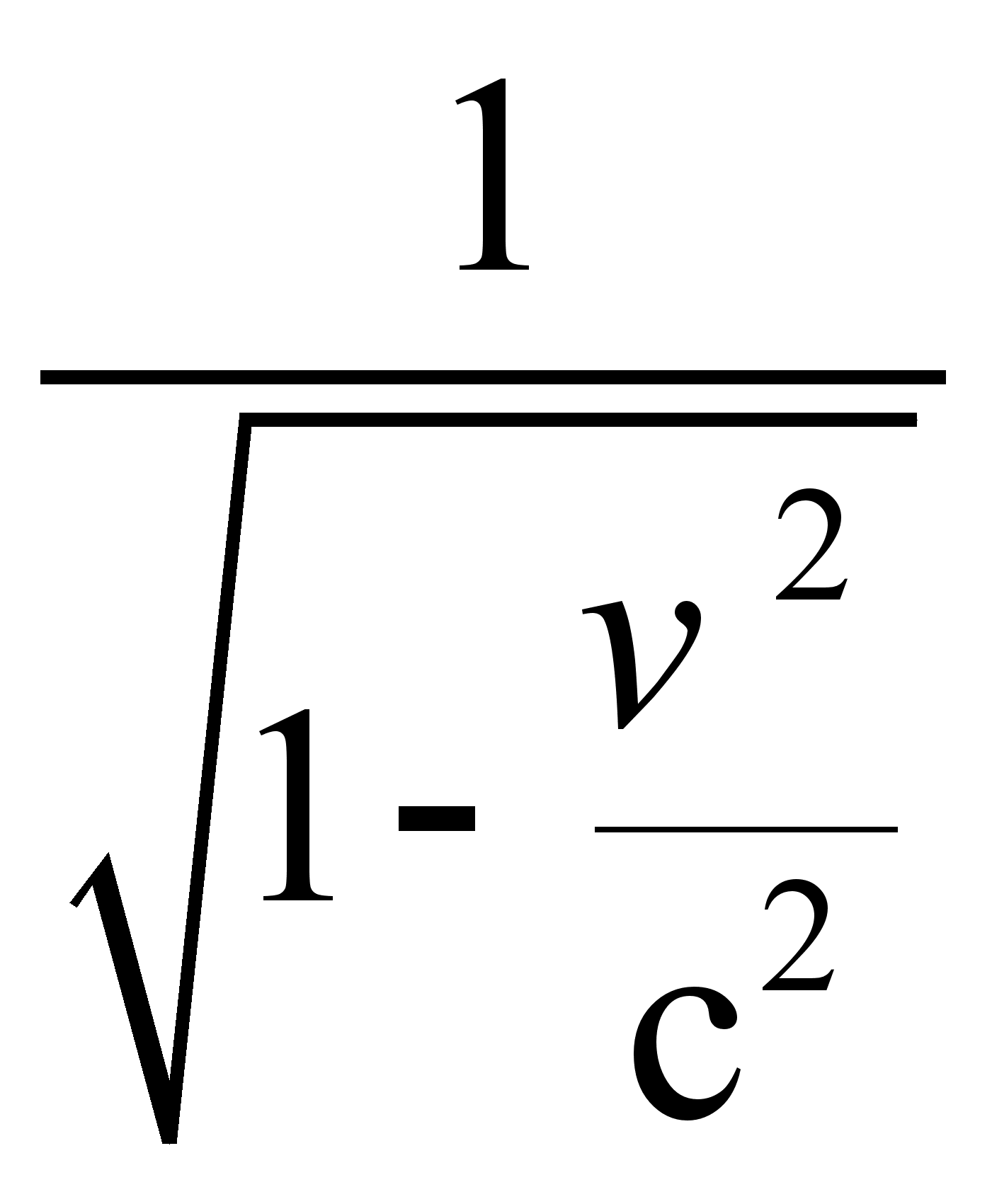 и для малых скоростей практически равны.
и для малых скоростей практически равны.
Учтём, что силы тоже преобразуются при переходе от одной системы отсчёта к другой. Импульс частицы в направлении перпендикулярно скорости движения не меняется.
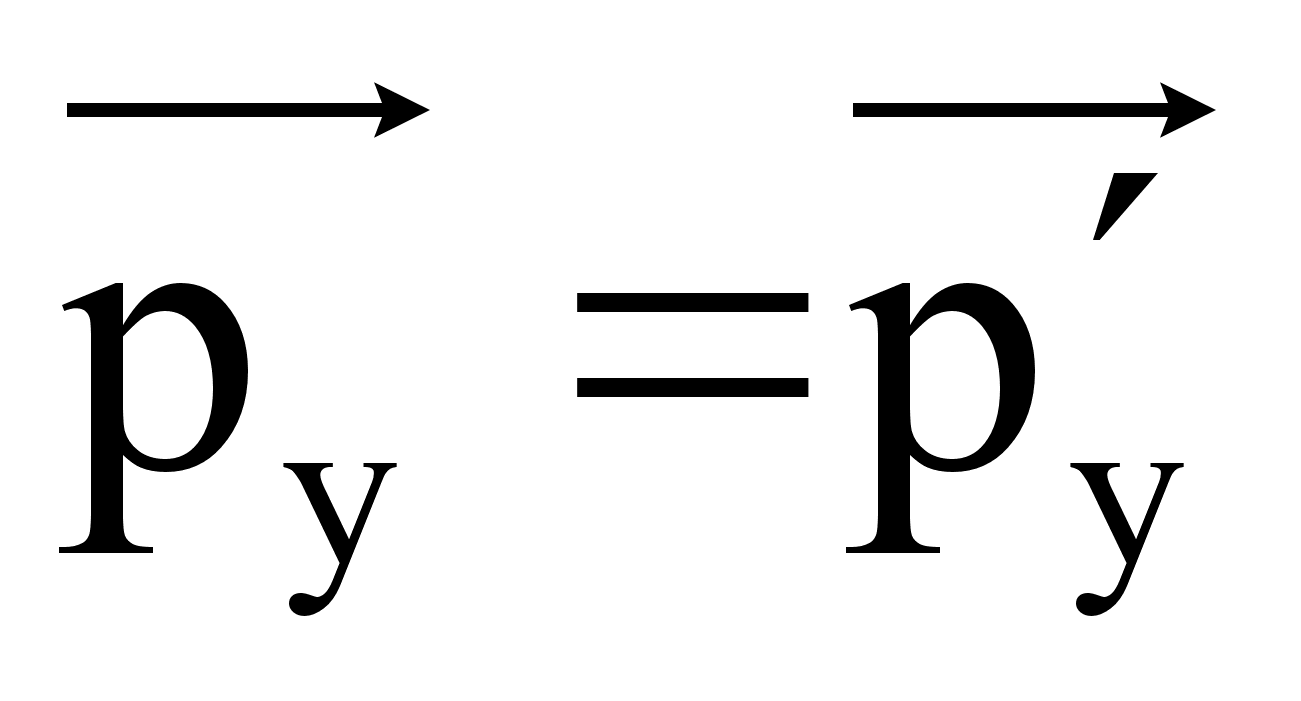
Рассматривая уравнение движения  , приходим к выводу, что за время
, приходим к выводу, что за время  частица приобретёт импульс
частица приобретёт импульс 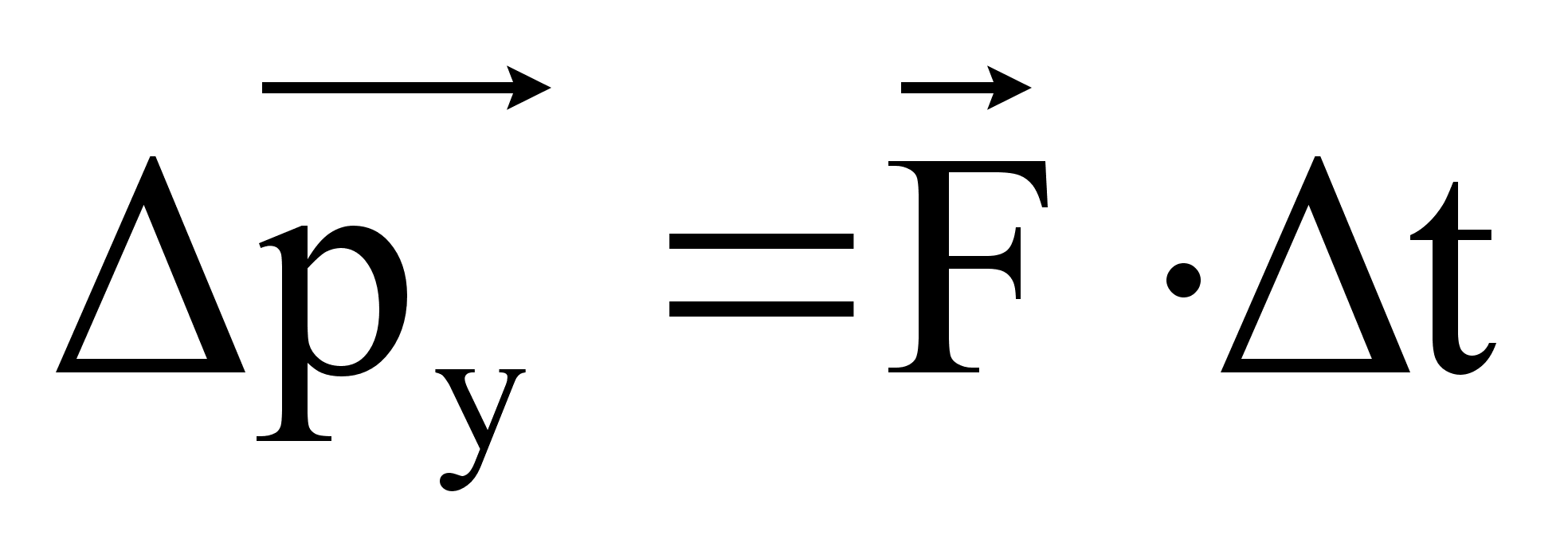 в системе К
в системе К
(Рисунок)
В системе 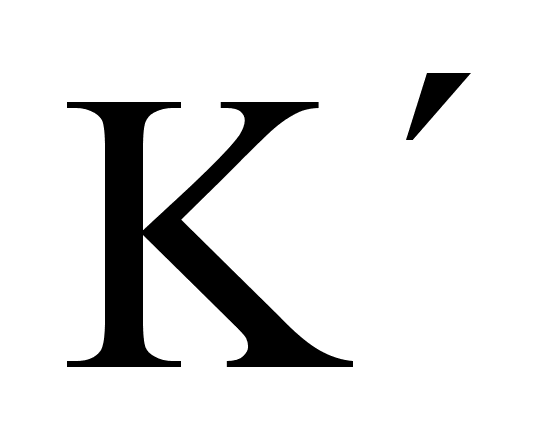 импульс будет равен
импульс будет равен 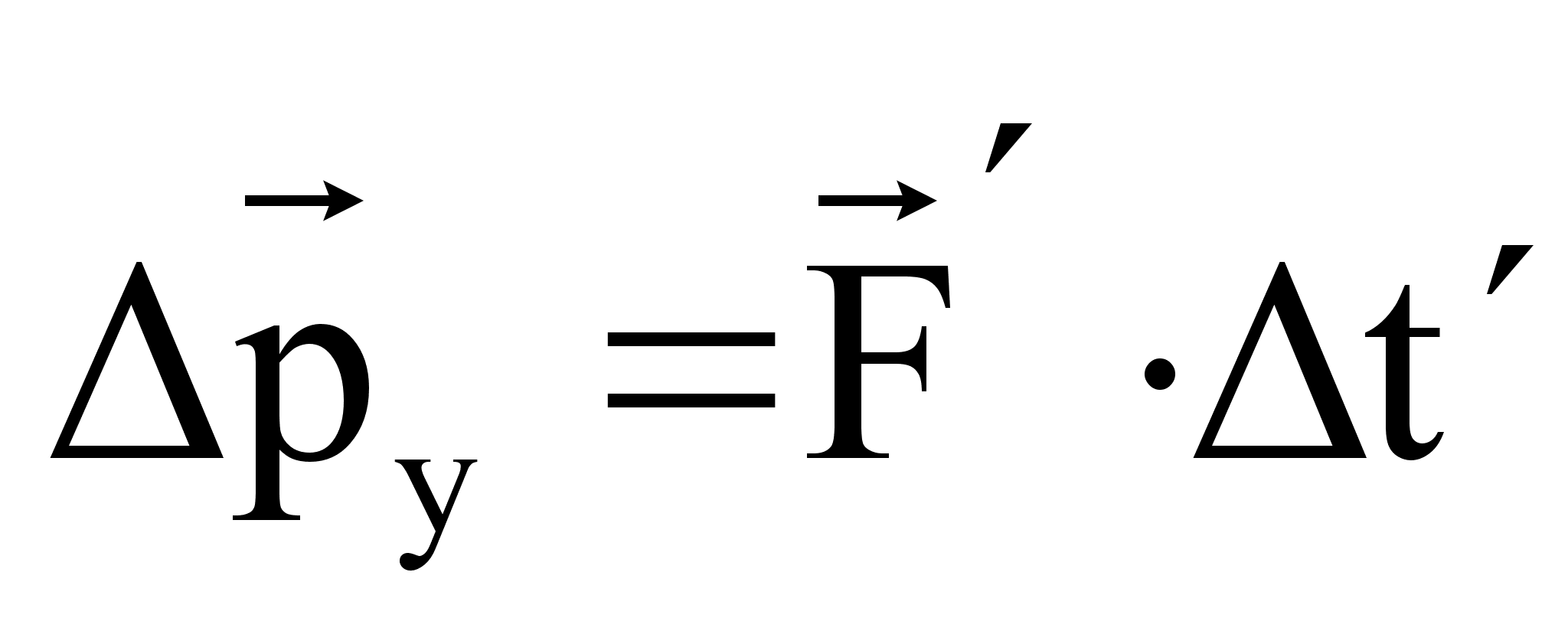 .
.
Так как система 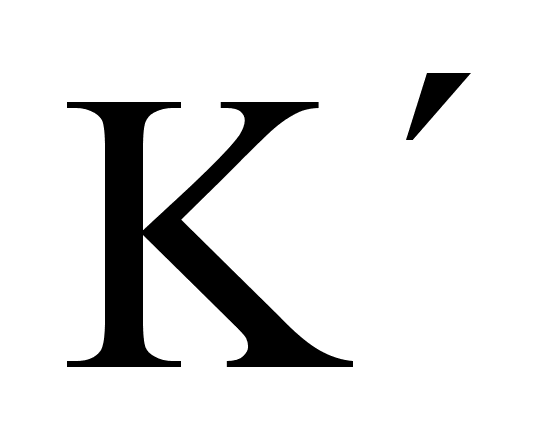 движется, то
движется, то 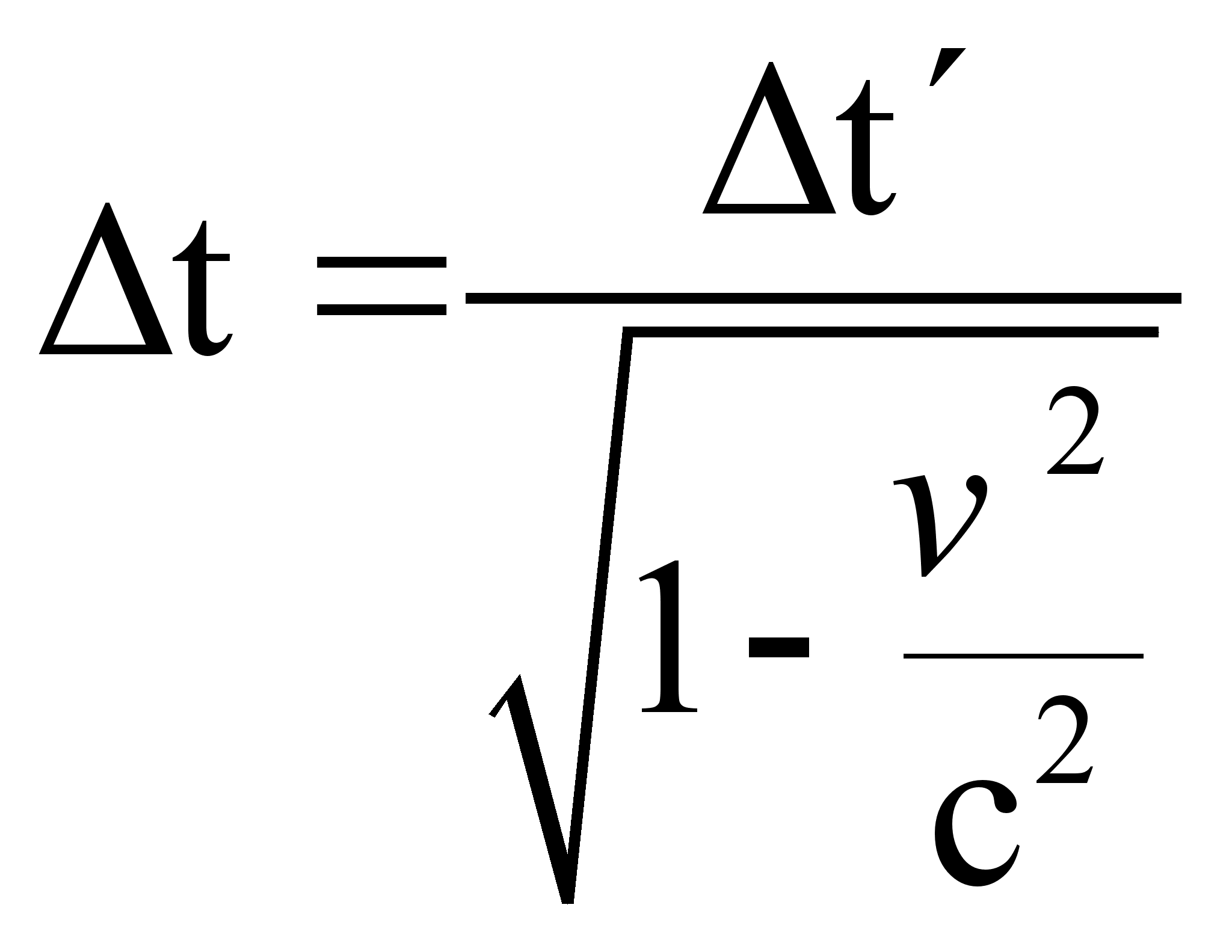 .
.
Учитывая выражение для F и 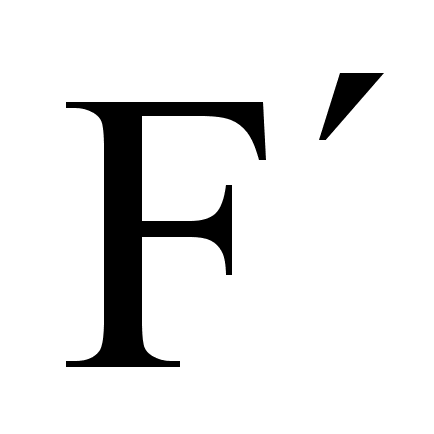 , и
, и 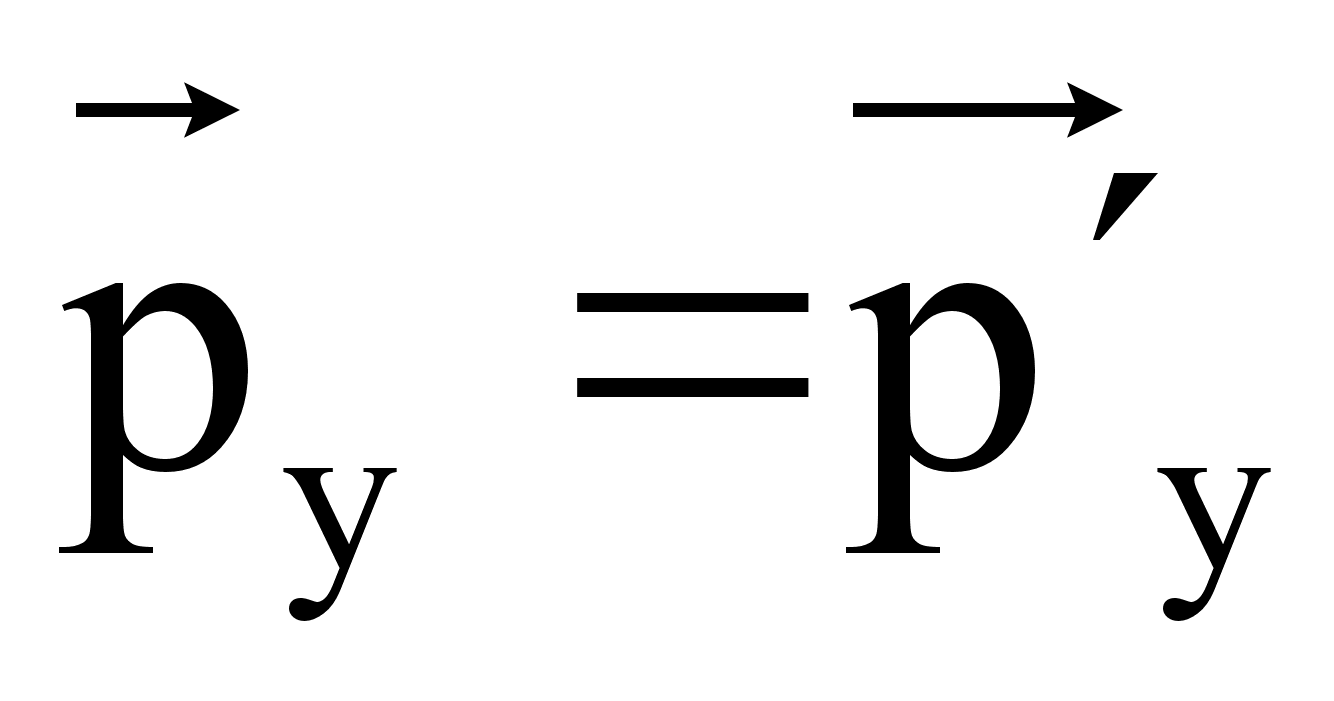 , получим
, получим
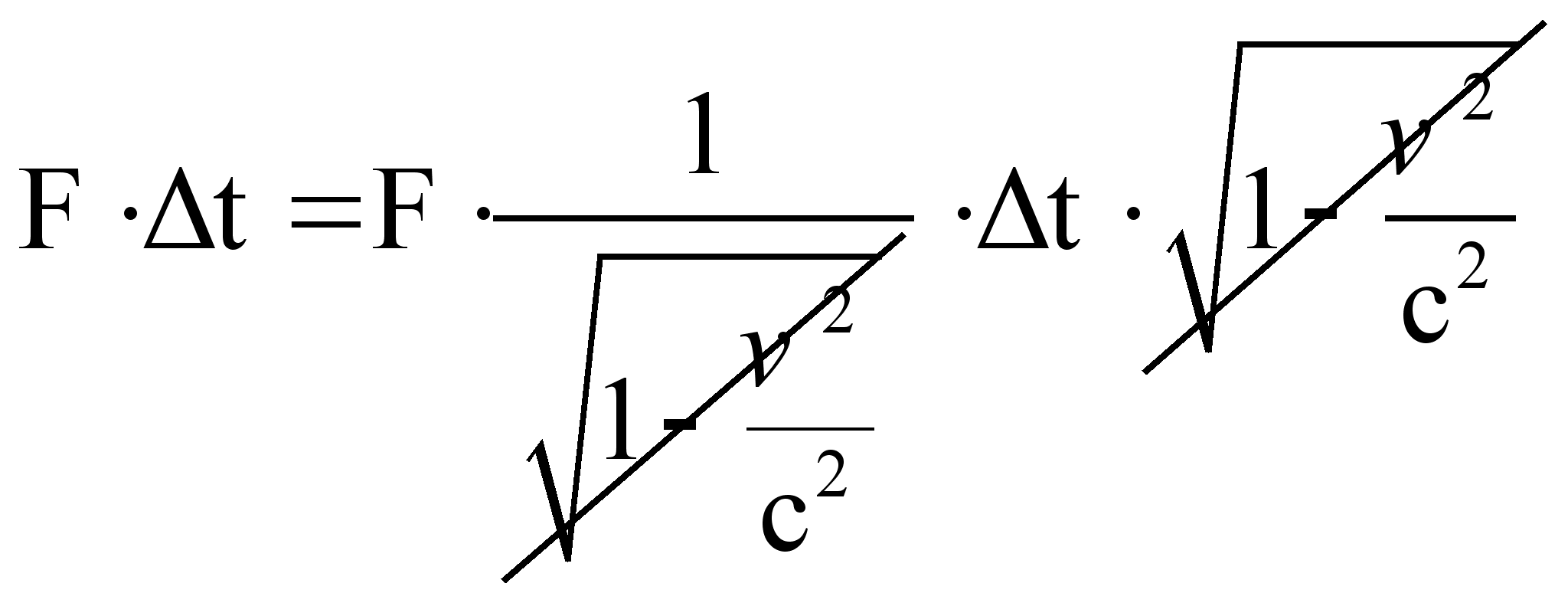
То есть один и тот же результат не зависимо от того, анализируем ли движение летящей заряженной частицы относительно проволоки с током или движение проволоки с током относительно неподвижно заряженной частицы.
В первом случае сила была чисто магнитная, во втором случае – чисто электрическая.
Если бы взяли другую систему координат, то нашли бы некоторую совокупность электрических и магнитных полей. Электрические и магнитные силы составляют части одного физического явления – электромагнитного взаимодействия частиц.
Разделение этого взаимодействия на электрические и магнитные части зависит от системы отсчёта, в которой мы описываем взаимодействие. Но полный электромагнитное описание инвариантно, полностью согласуется с принципом относительности Эйнштейна.
Поле движущегося заряда.
Пространство изотропно, поэтому, если заряд неподвижен, все направления оказываются равноправны. Поэтому создаваемая точечным зарядом электростатическое поле является сферически симметричным. В случае движения заряда с постоянной скоростью относительно инерциальной системы отсчёта, в пространстве появляется выделенное напряжение в направлении в направлении вектора 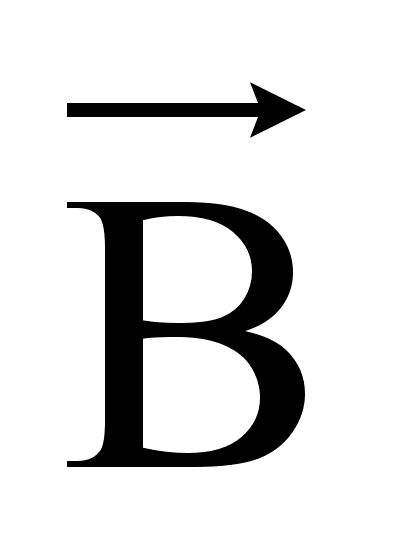 . Поэтому создаваемое движущимся зарядом магнитное поле обладает осевой симметрией относительно вектора скорости.
. Поэтому создаваемое движущимся зарядом магнитное поле обладает осевой симметрией относительно вектора скорости.
Рассмотрим магнитное поле, создаваемое точке магнитного поля точечным зарядом q, который движется со скоростью 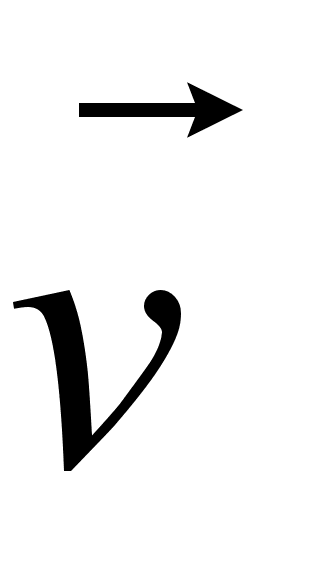 в вакууме.
в вакууме.
Если (с – скорость света в вакууме), то можно заключить:
(с – скорость света в вакууме), то можно заключить:

(Рисунок)
Учитывая, что из эксперимента следует  , получим:
, получим:
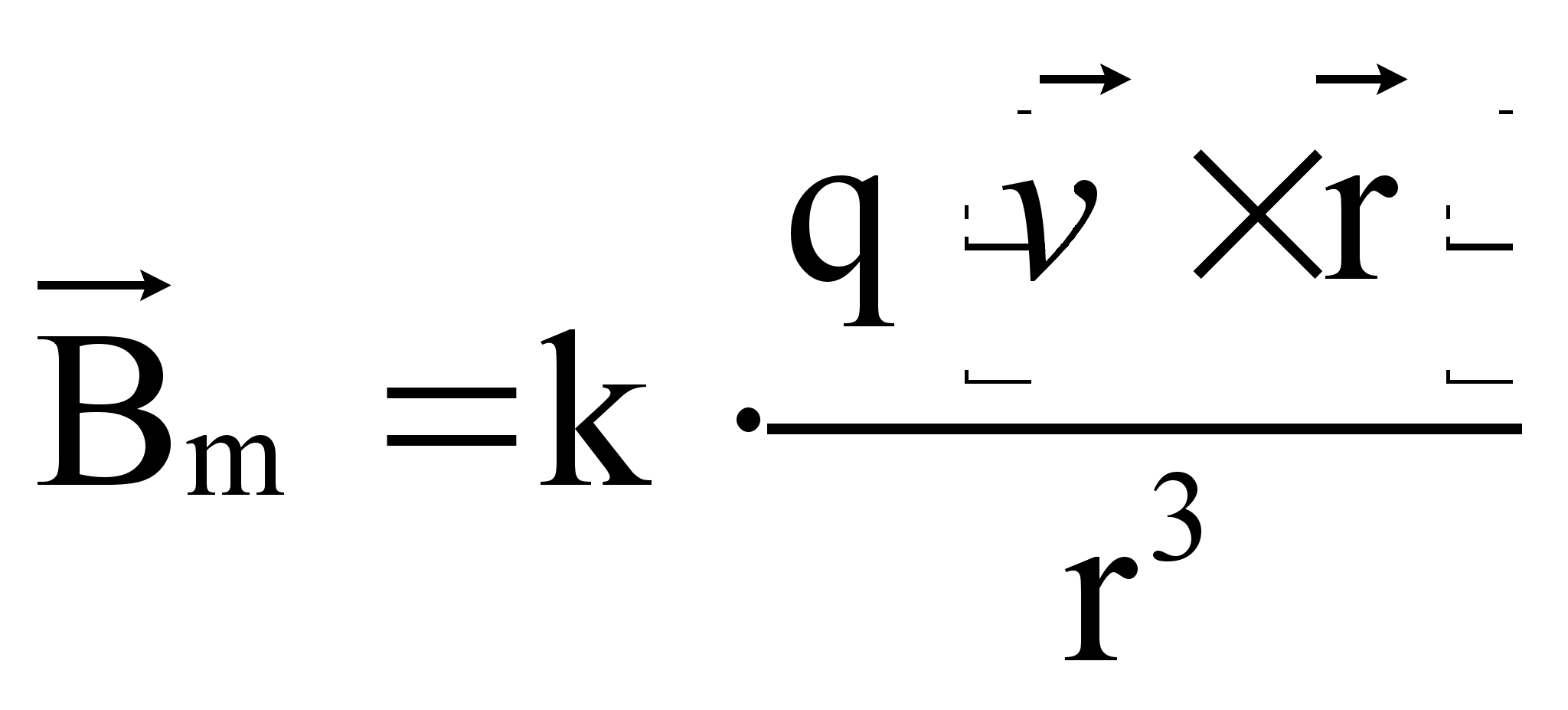 (55)
(55)
Постоянную k можно определить только из эксперимента. Как показали расчеты, при движении заряда q со скоростью 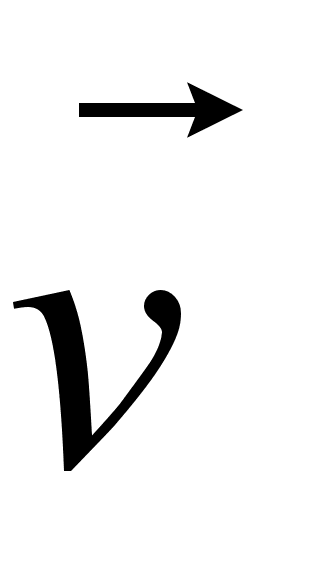 , близкой к скорости света, утрачивается сферическая симметрия электрического поля.
, близкой к скорости света, утрачивается сферическая симметрия электрического поля.
Поле сплющивается в направлении движения.
(Рисунок)
Закон Био-Савара-Лапласа.
Из опытных данных физики Био и Саваро, математик Лаплас получили формулу:
 (56)
(56)
где 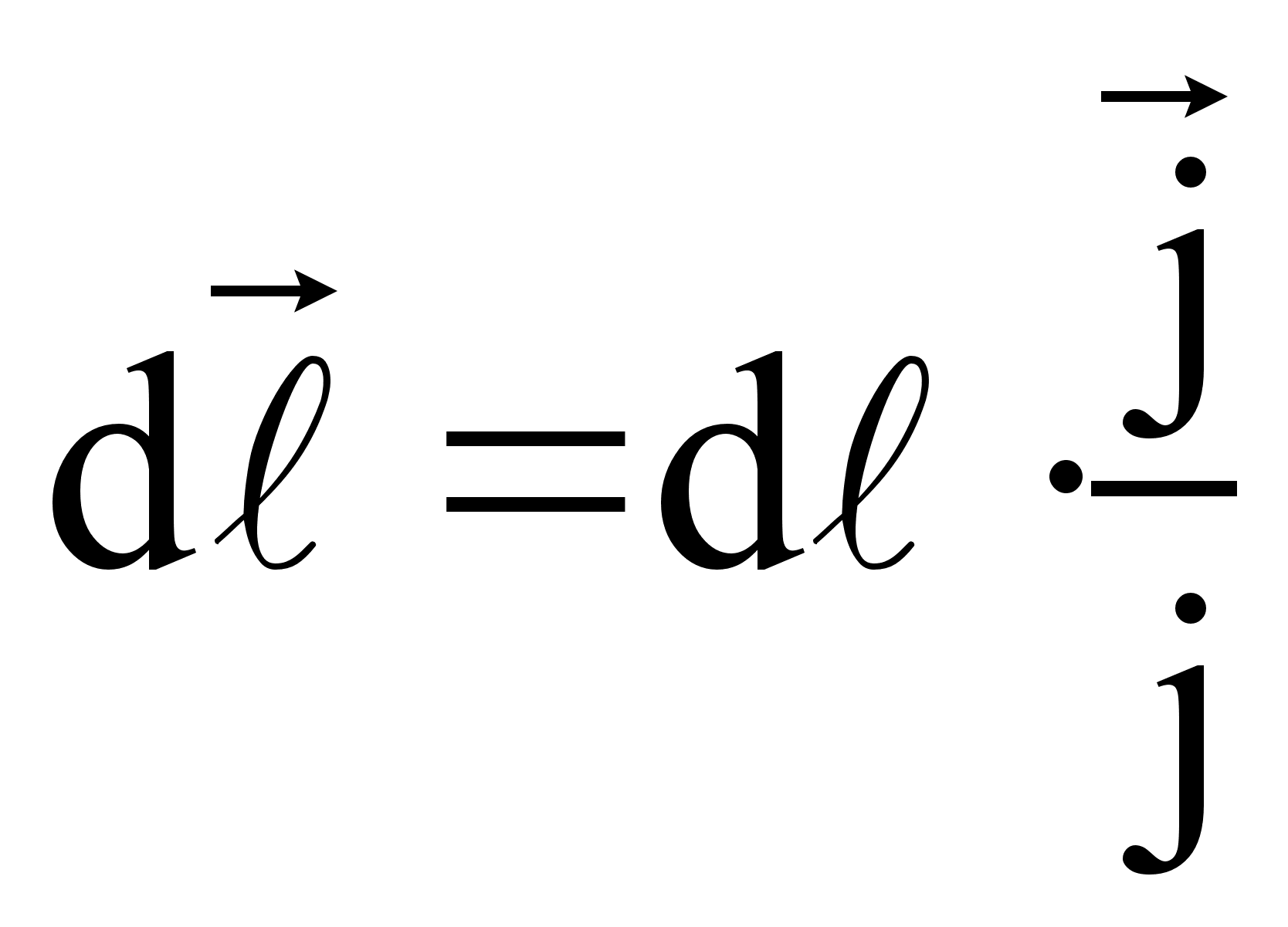 - элемент длины проводника
- элемент длины проводника
 - вектор, проведённый из элемента
- вектор, проведённый из элемента 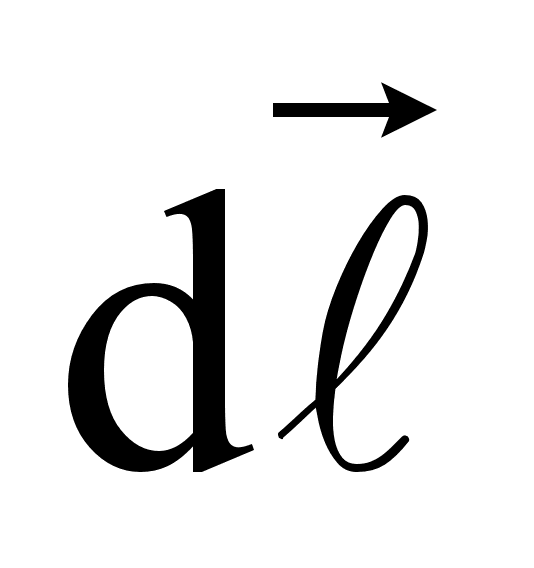 в рассматриваемой точке поля,
в рассматриваемой точке поля,
а 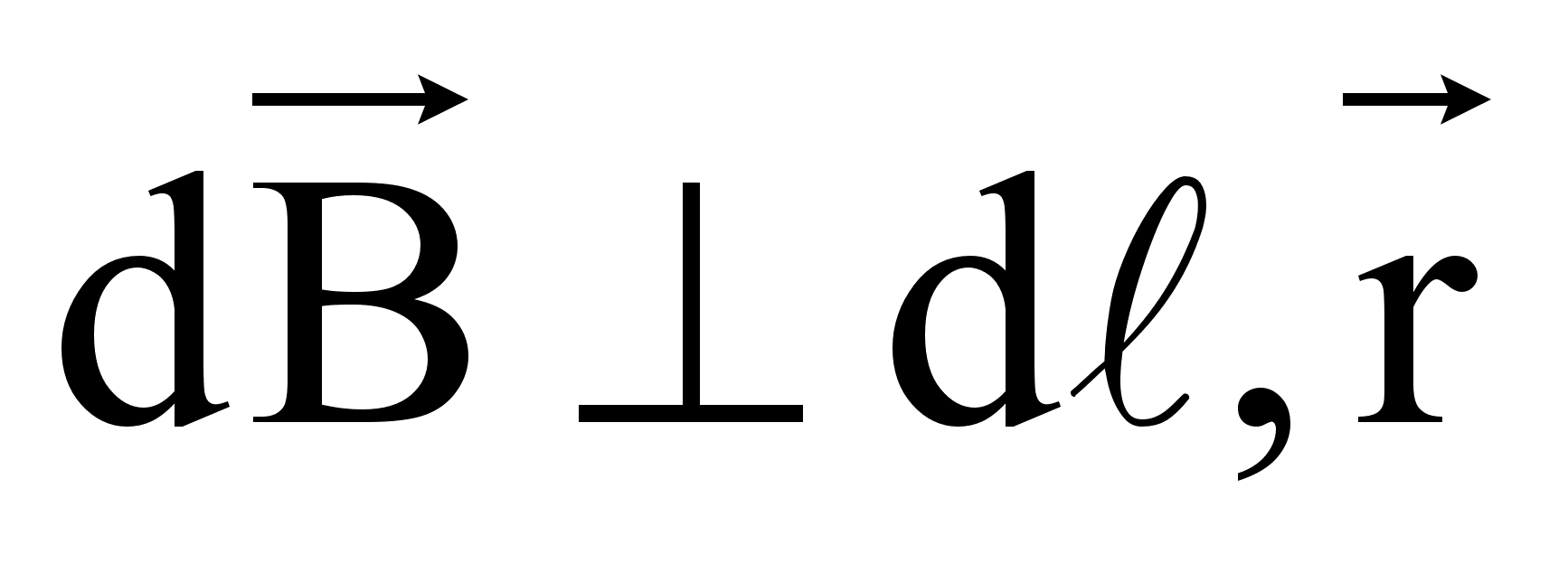
Направление вектора магнитной индукции находится по правилу правого винта.
(Рисунок)
Модуль вектора магнитной индукции определяется по формуле:
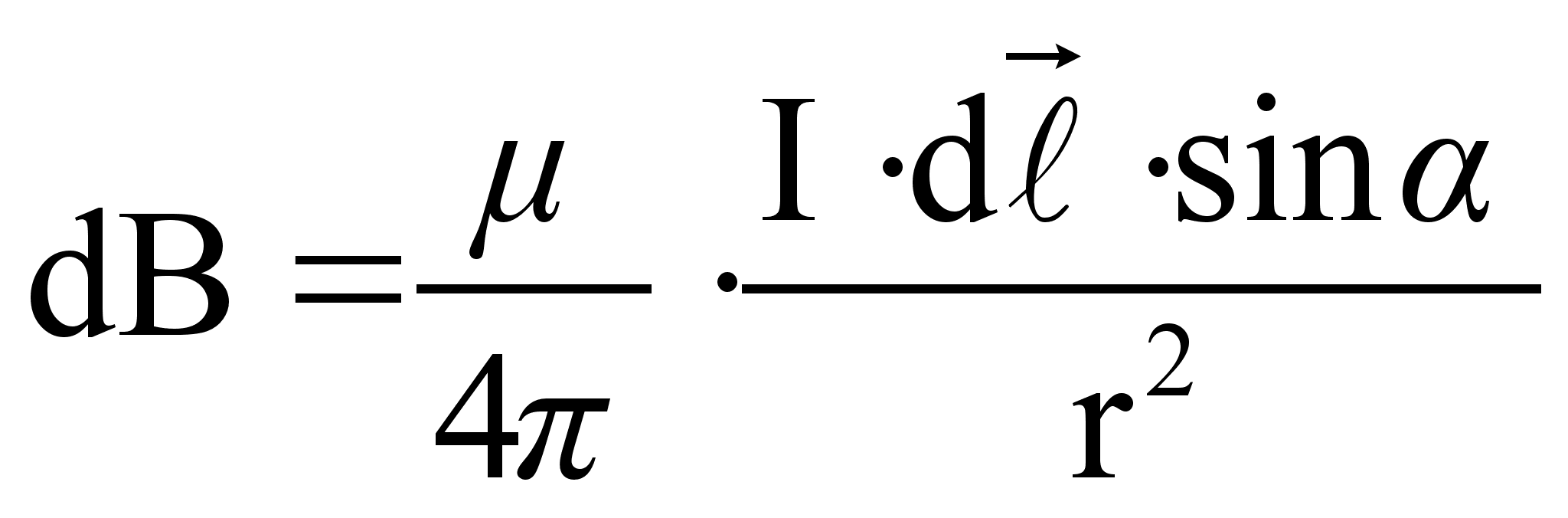 (57)
(57)
Из принципа суперпозиции следует, что вектор магнитной индукции в произвольной точке магнитного поля в проводнике с током 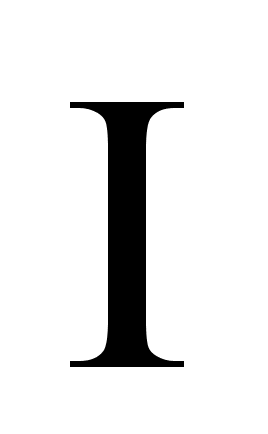 равен:
равен:
 (58)
(58)
где  - магнитная индукция поля, создаваемая элементом проводника длиной
- магнитная индукция поля, создаваемая элементом проводника длиной 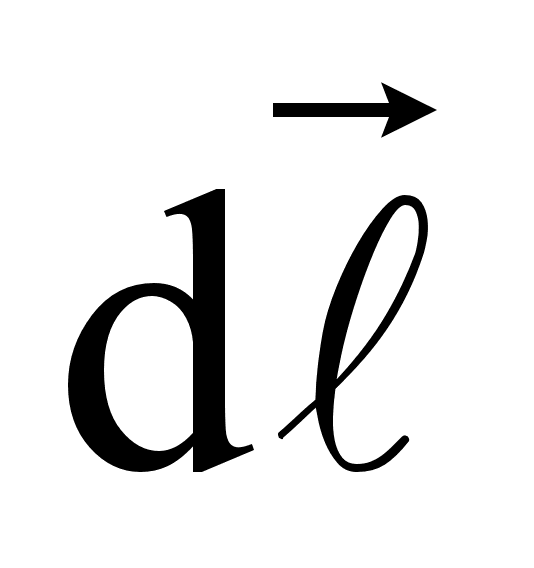 .
.
Сила Лоренца.
На движущийся в магнитном поле электрический заряд действует сила:
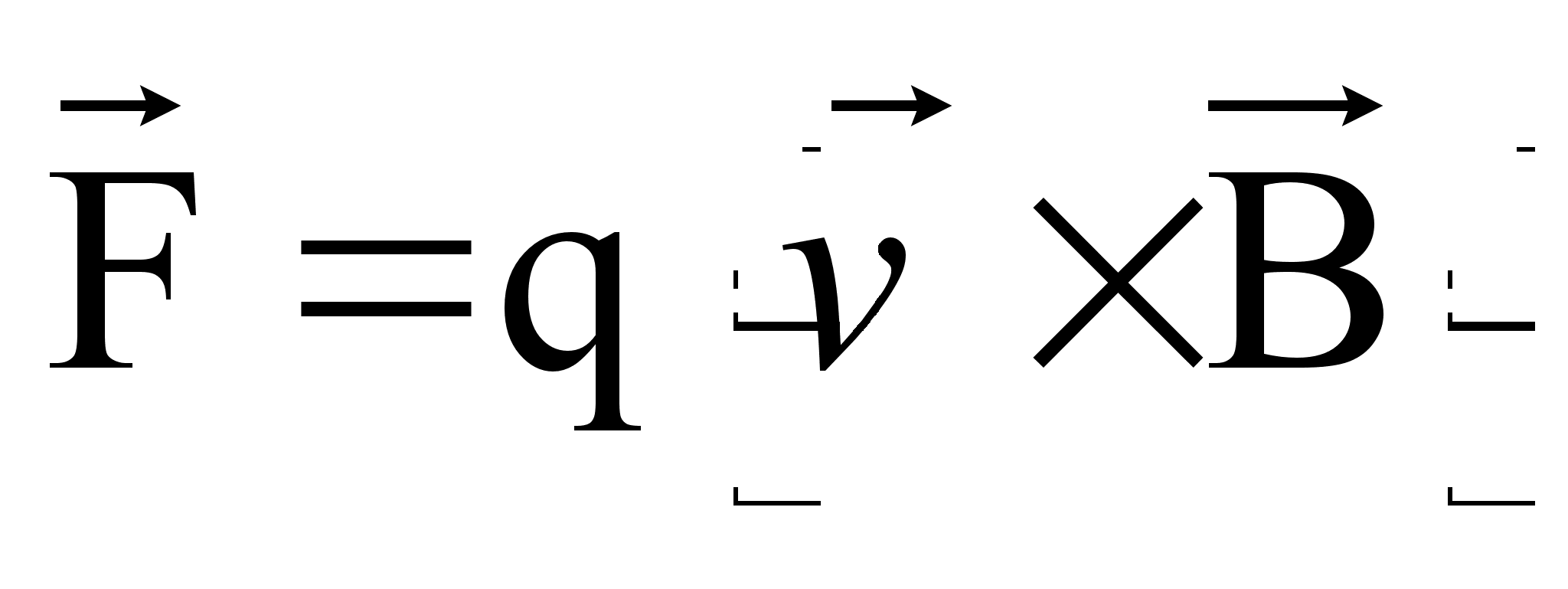 (69)
(69)
где q – величина заряда
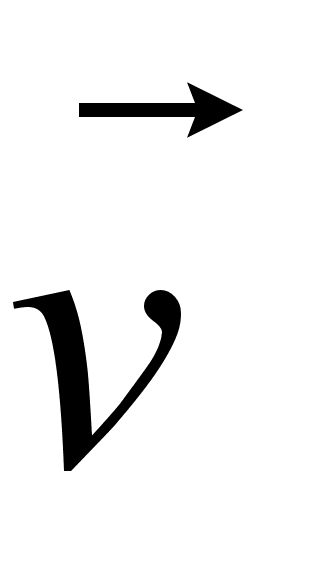 - вектор скорости заряда
- вектор скорости заряда
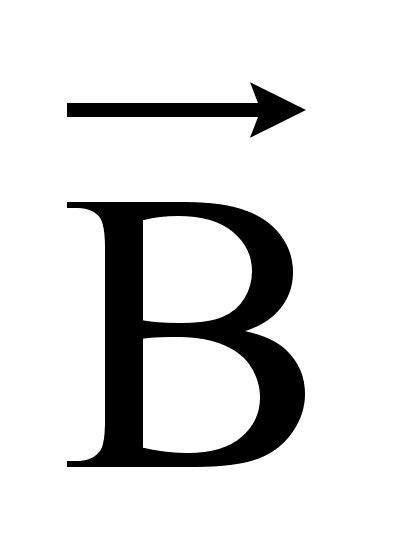 - вектор магнитной индукции поля.
- вектор магнитной индукции поля.
Направление силы Лоренца определяется по правилу левой руки.
(Рисунок)
Модуль силы Лоренца находим по формуле:
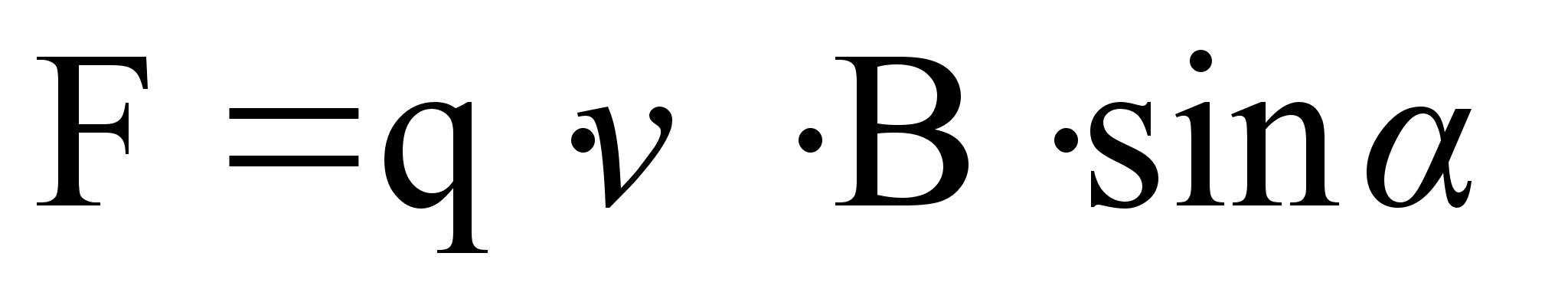
Так как 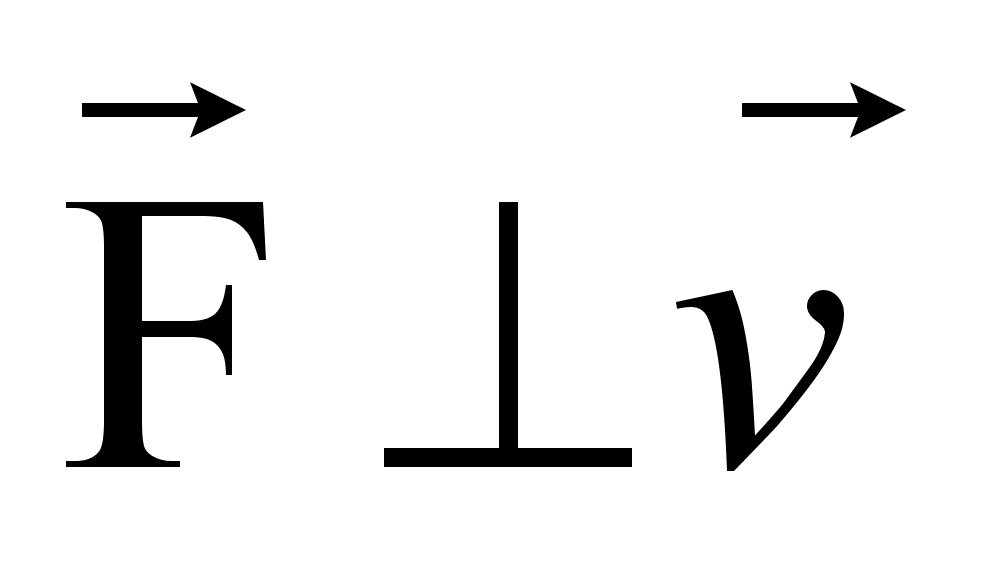 , то сила Лоренца работы не совершает, значит кинетическая энергия движущейся частицы не изменяется.
, то сила Лоренца работы не совершает, значит кинетическая энергия движущейся частицы не изменяется.
Если заряженная частица влетает в магнитное поле перпендикулярно линиям магнитной индукции, то она будет двигаться по окружности радиуса R/
 ,
, 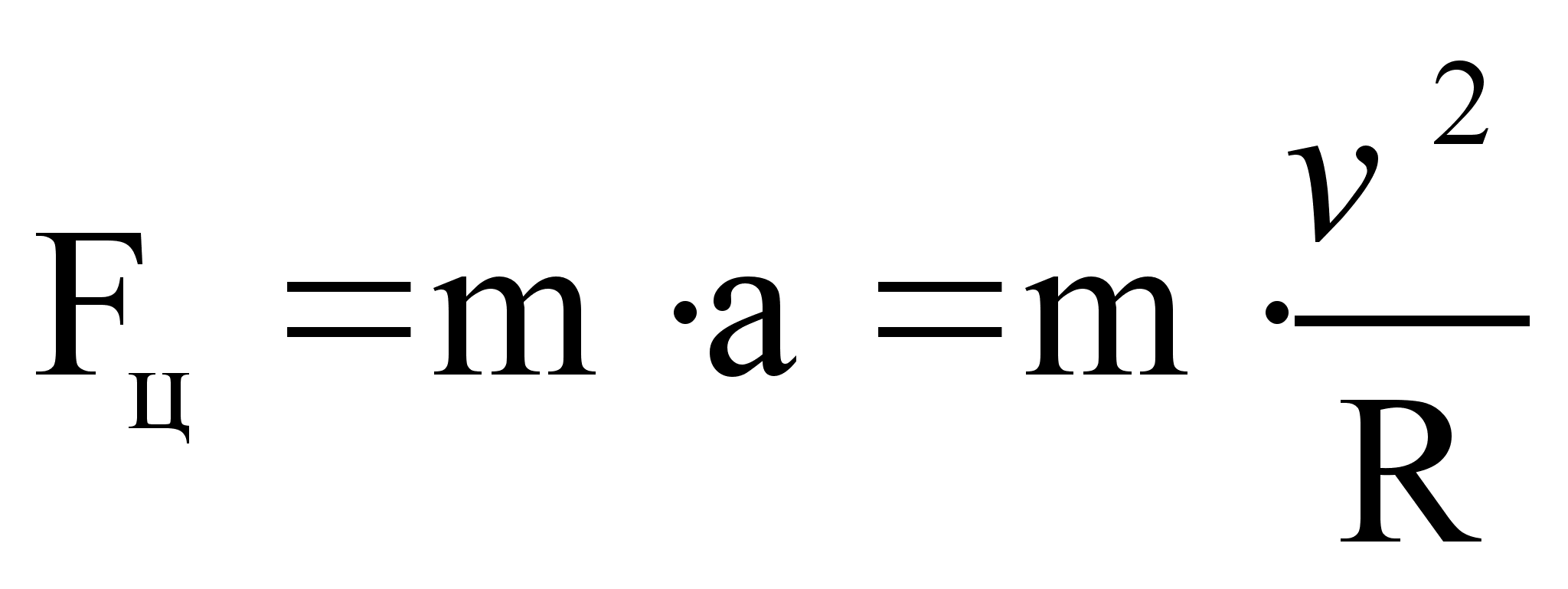 ,
, 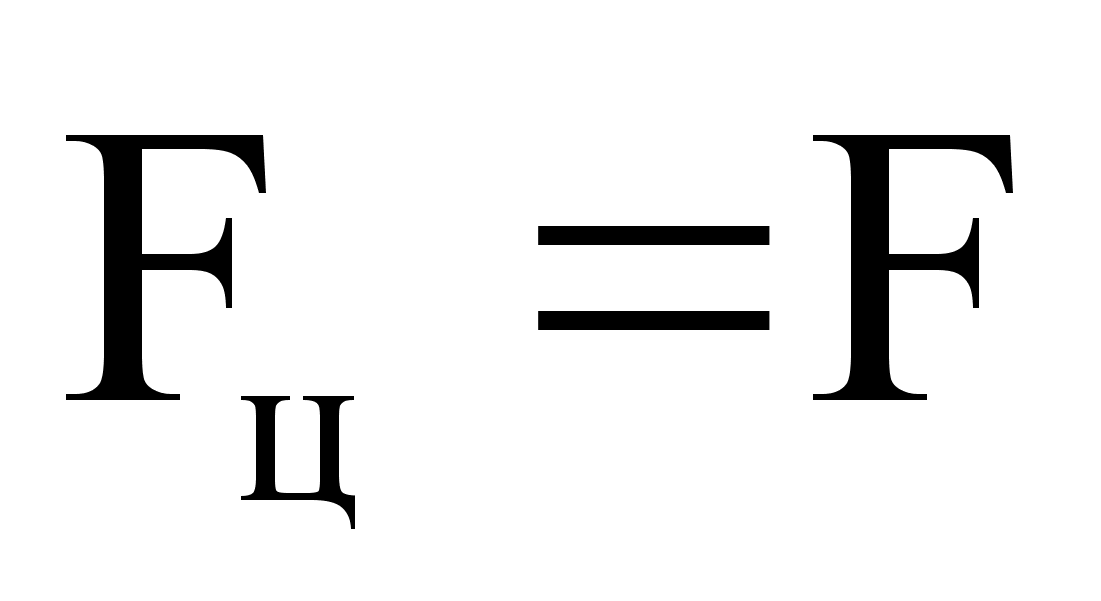 ,
,
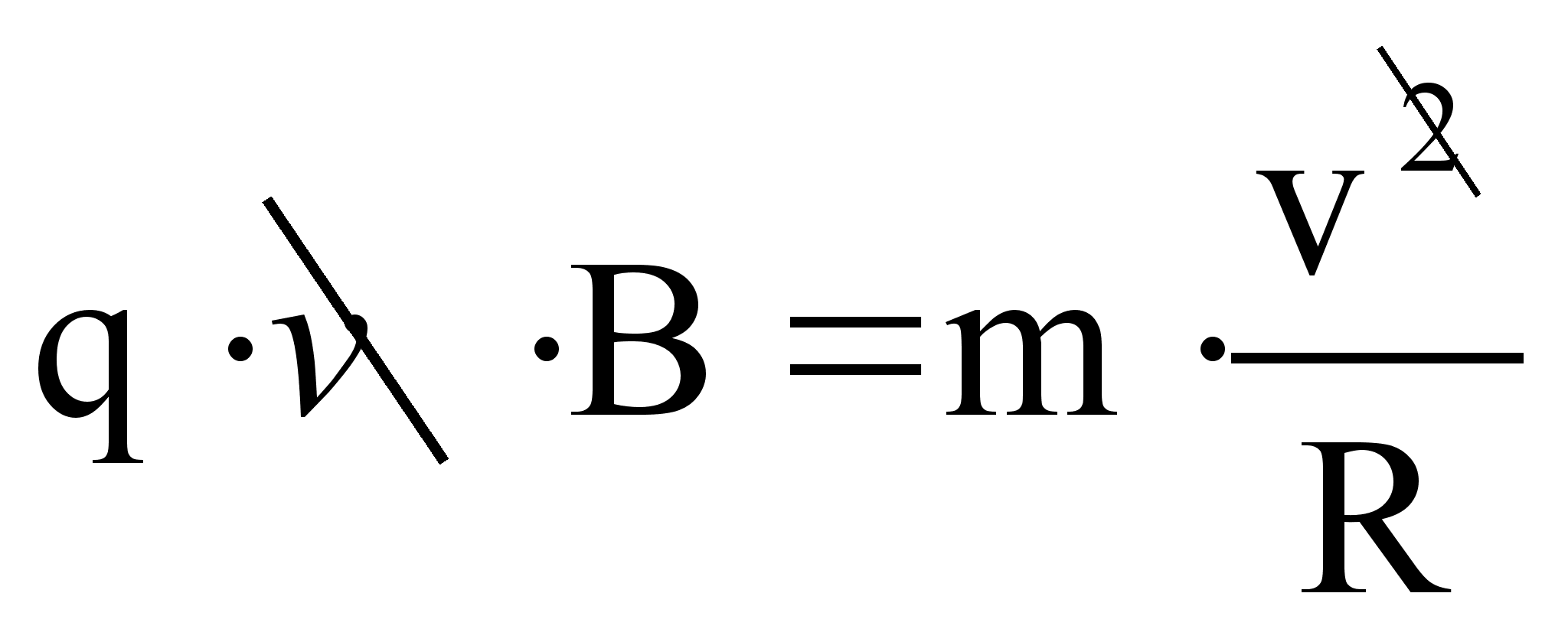
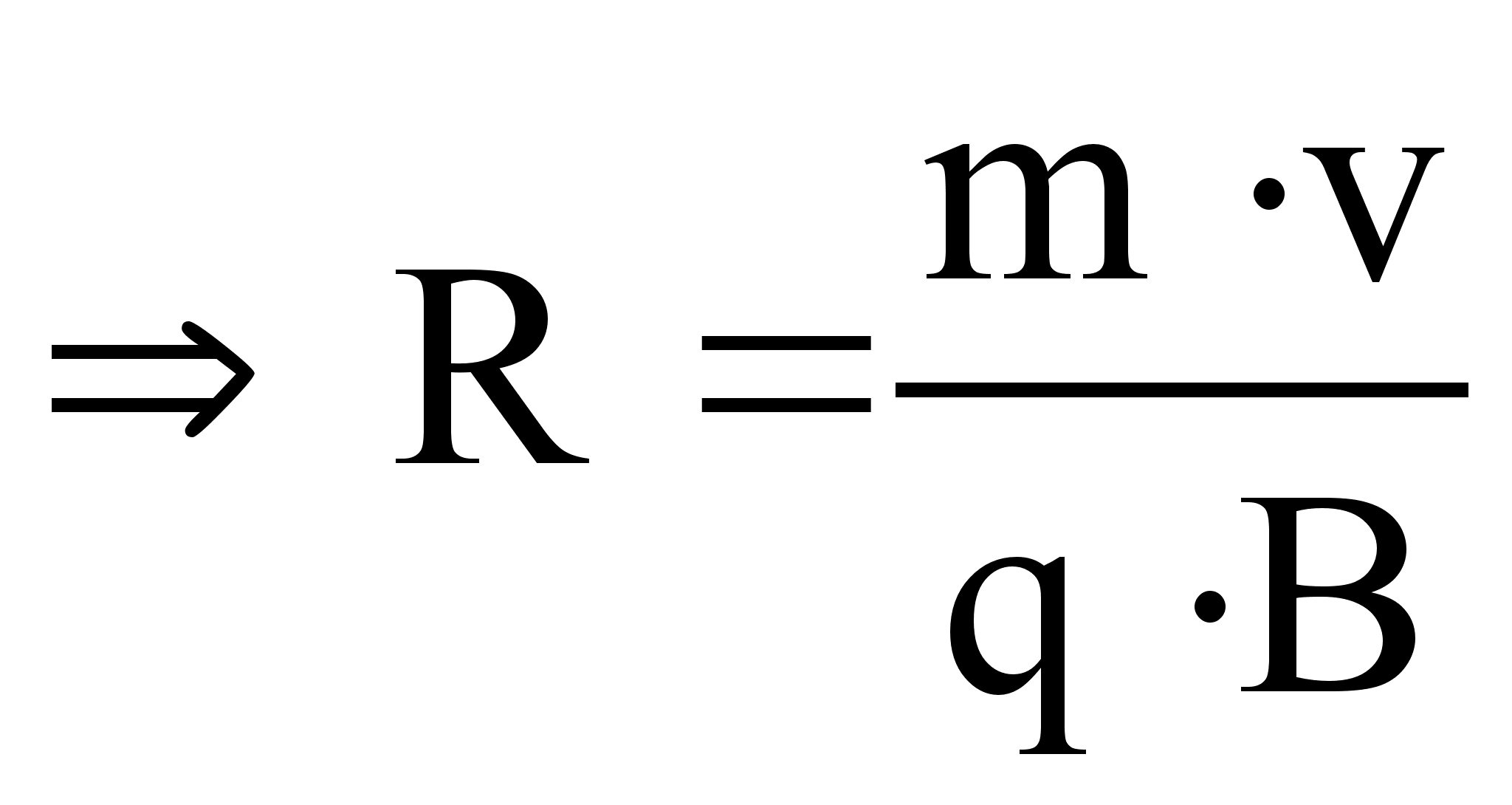
Если заряженная частица влетает под некоторым углом, меньшим 90 к линиям магнитной индукции, то её траекторией будет винтовая линия.
к линиям магнитной индукции, то её траекторией будет винтовая линия.
Если на движущийся электрический заряд действует магнитное поле и электростатическое поле, то
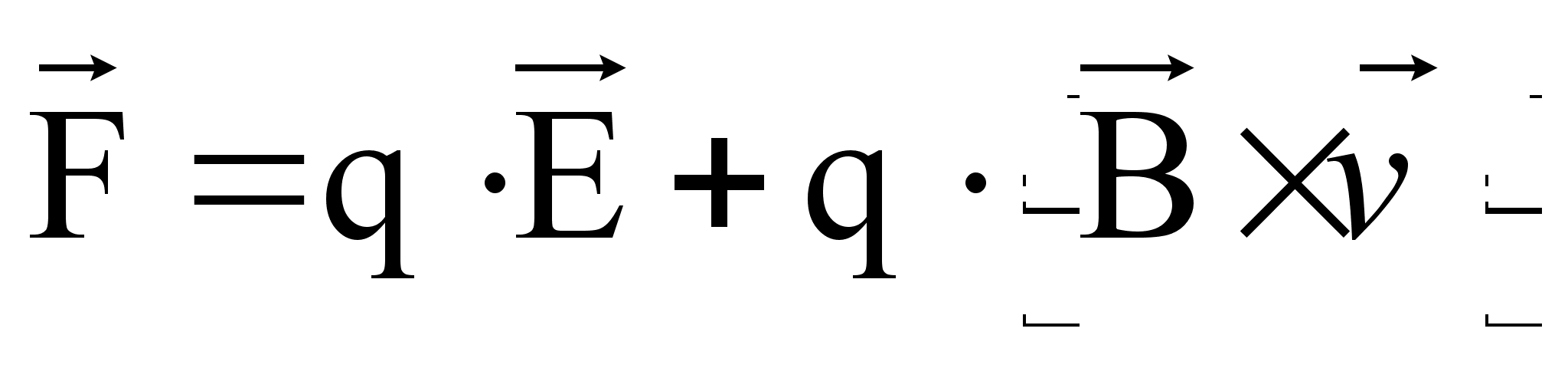 (71)
(71)
(Рисунок)
Дивергенция и ротор магнитного поля.
Отсутствие в природе магнитных зарядов свидетельствует о том, что линии магнитной индукции не имеют ни начала, ни конца. Поэтому поток вектора магнитной индукции 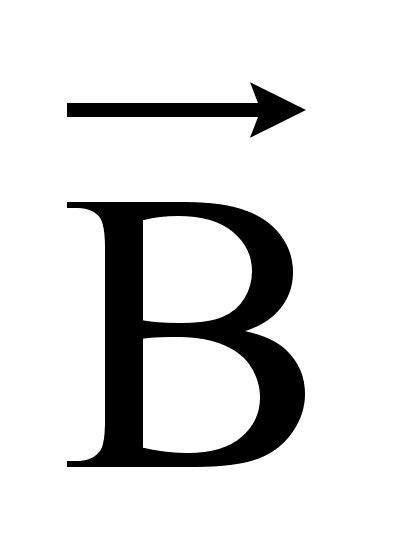 через замкнутую поверхность.
через замкнутую поверхность.
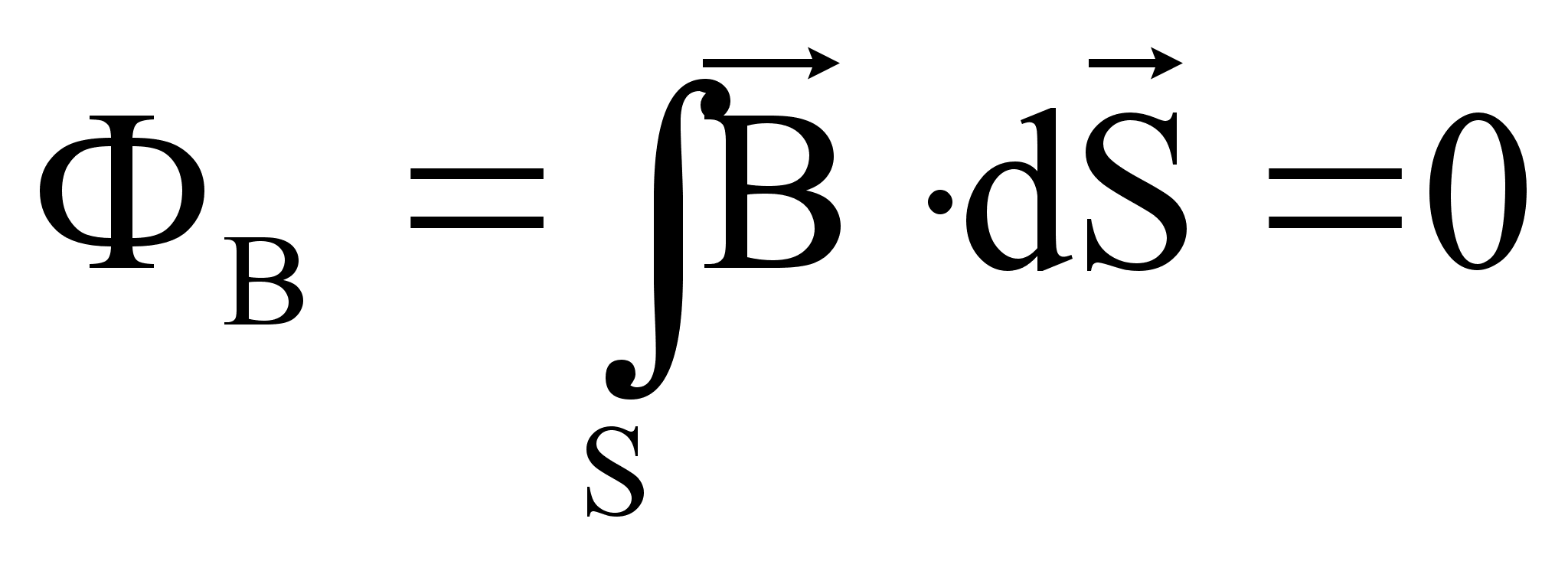
Заменим в соответствии с теоремой Гаусса интеграл, получим:
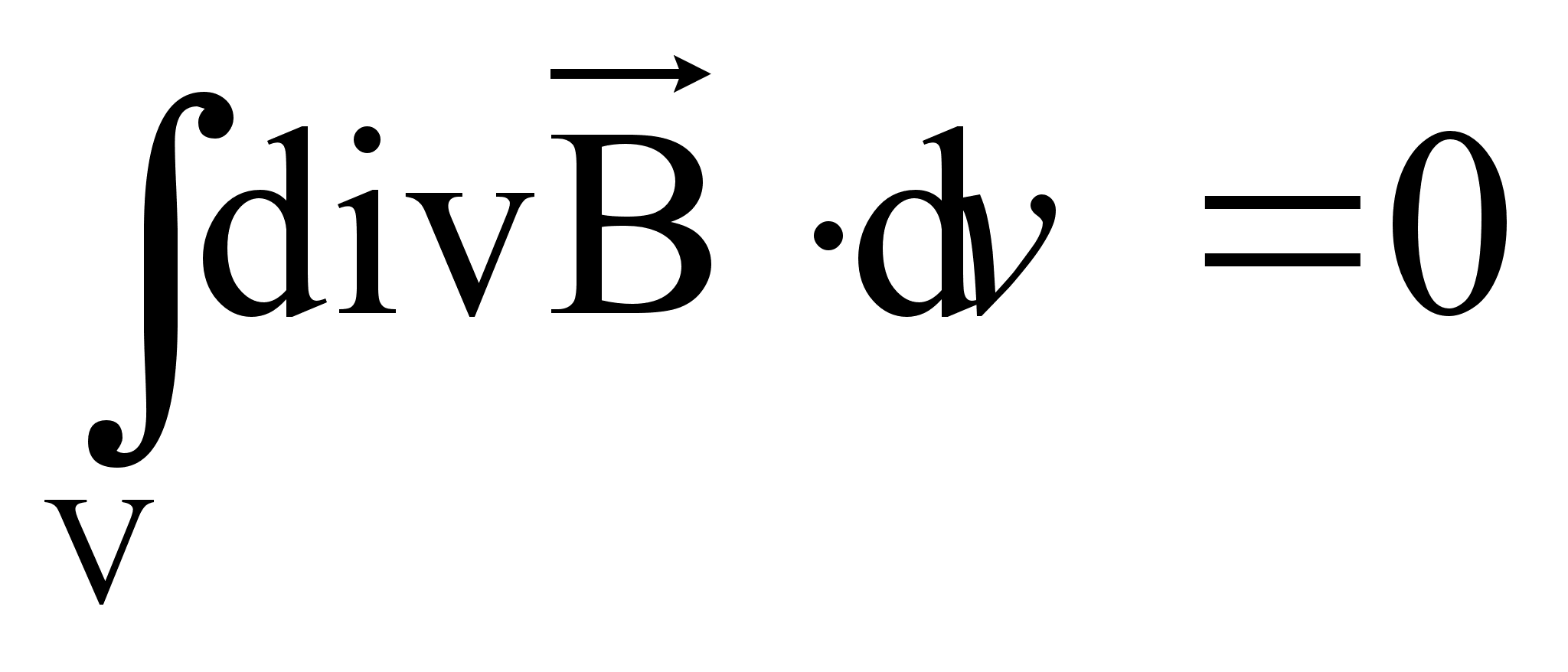
Это условие выполняется только в том случае, если в каждой точке поля подынтегральная функция равна нулю.
 (72)
(72)
Таким образом, дивергенция магнитного поля равна нулю.
Рассмотрим циркуляцию вектора магнитной индукции -  .
.
Вычислим этот интеграл для прямого тока:
(Рисунок)
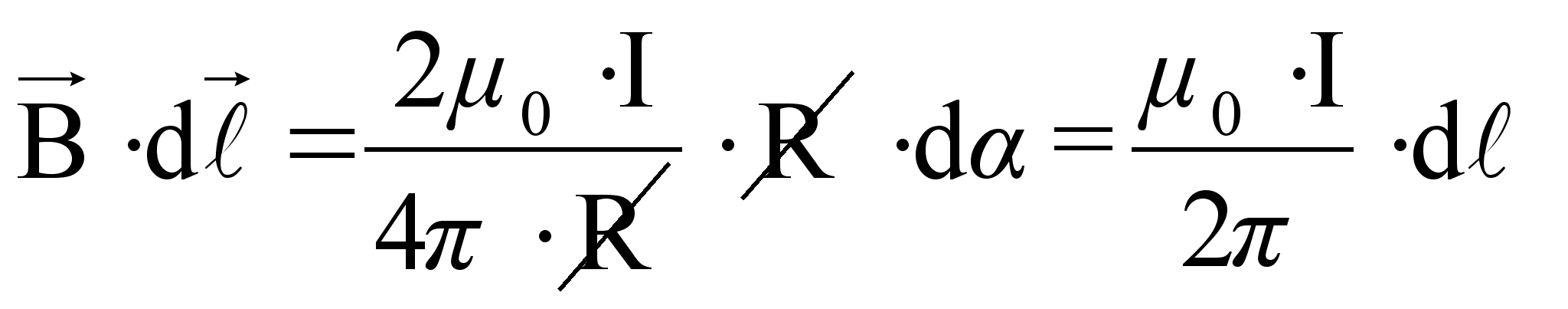
В левой части равенства – скалярное произведение.
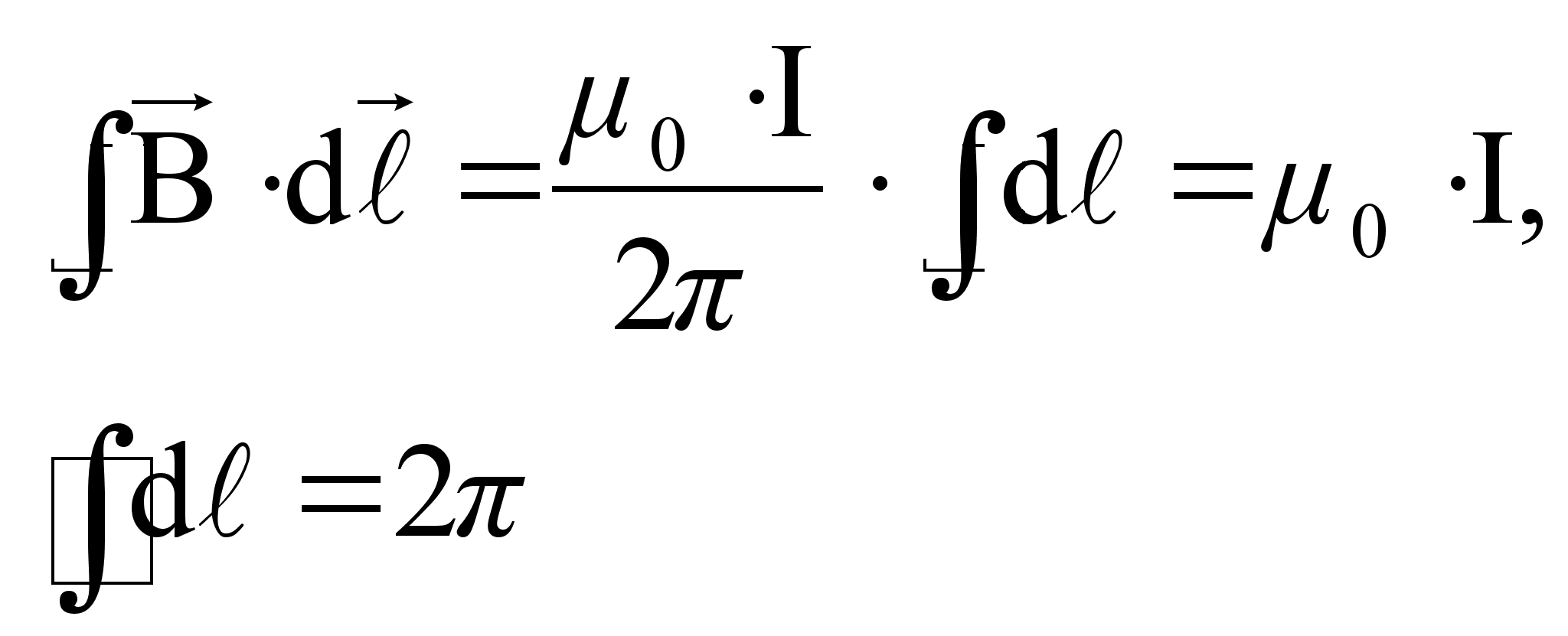 (73)
(73)
Если контур не охватывает проводник с током, то  .
.
(Рисунок)
Радиус сначала перемещается в направлении 1-2 (знак плюс), а затем обратно 2-1 (знак минус).
Таким образом, если контур не охватывает ток, то циркуляция равна нулю.
Формулу (73) можно обобщить на случай токов, текущих по проводам произвольной формы.
(Рисунок)
В силу принципа суперпозиции, можно заключить:
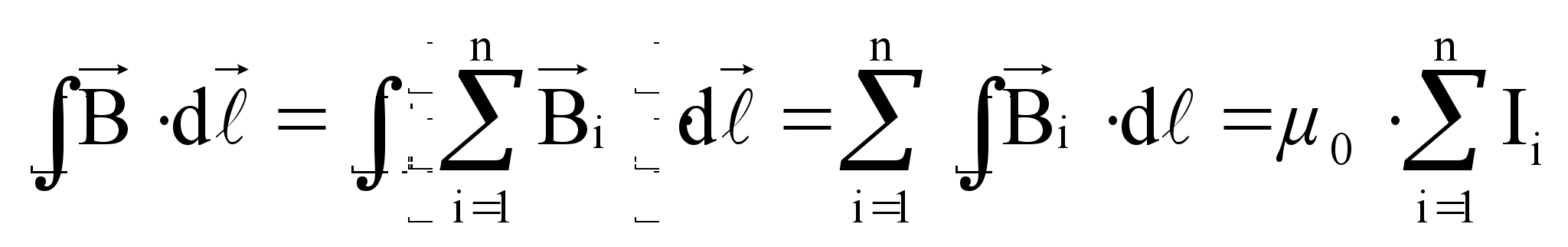
Если токи текут через всё пространство контура, то
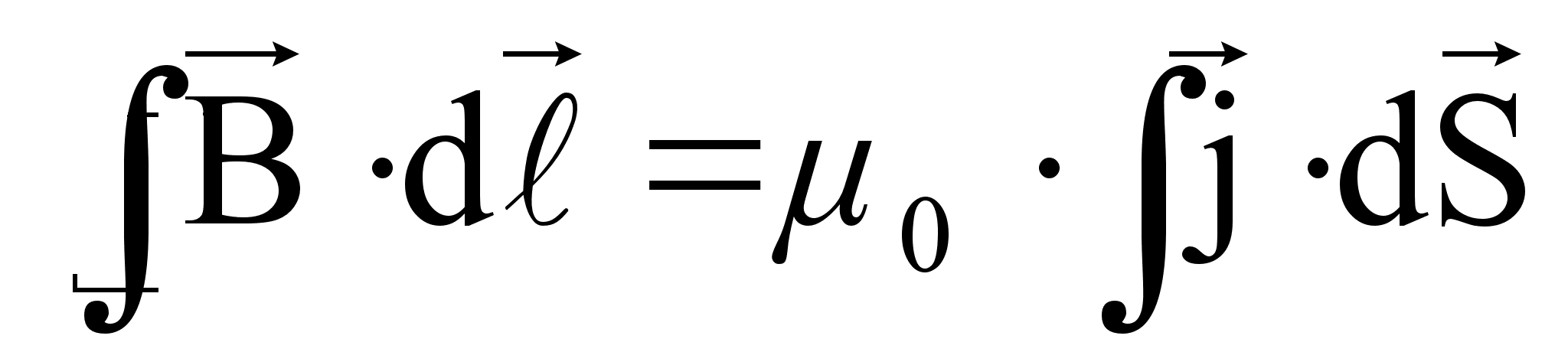 (74)
(74)
где  - плотность тока данной точки.
- плотность тока данной точки.
Сумма тока:
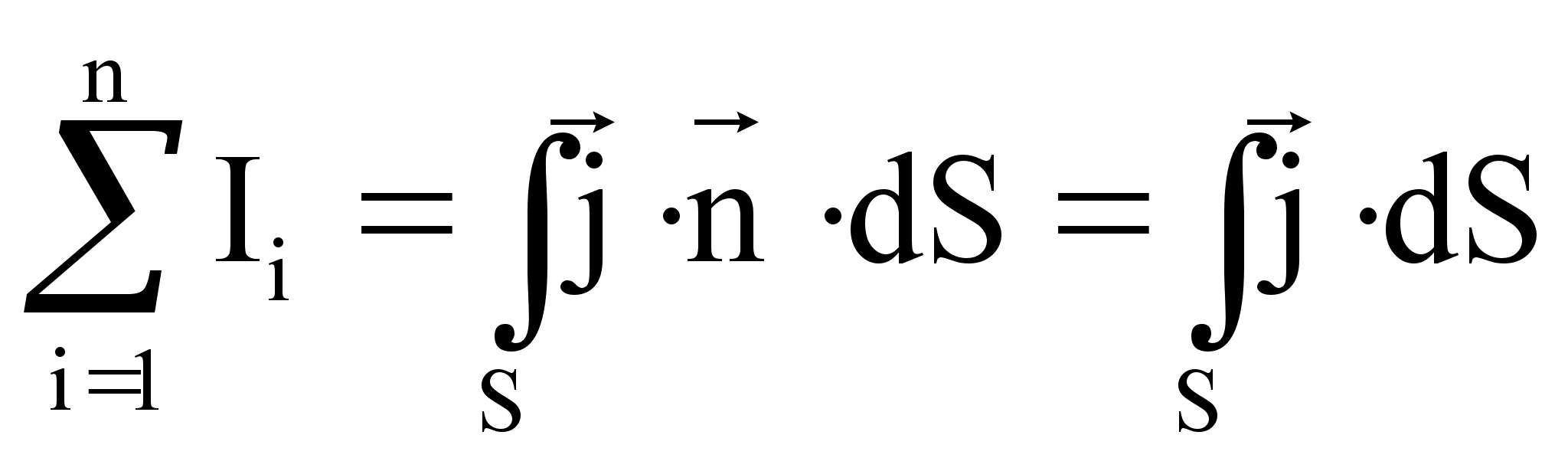
Преобразуем левую часть равенства (74) по теореме Стокса:
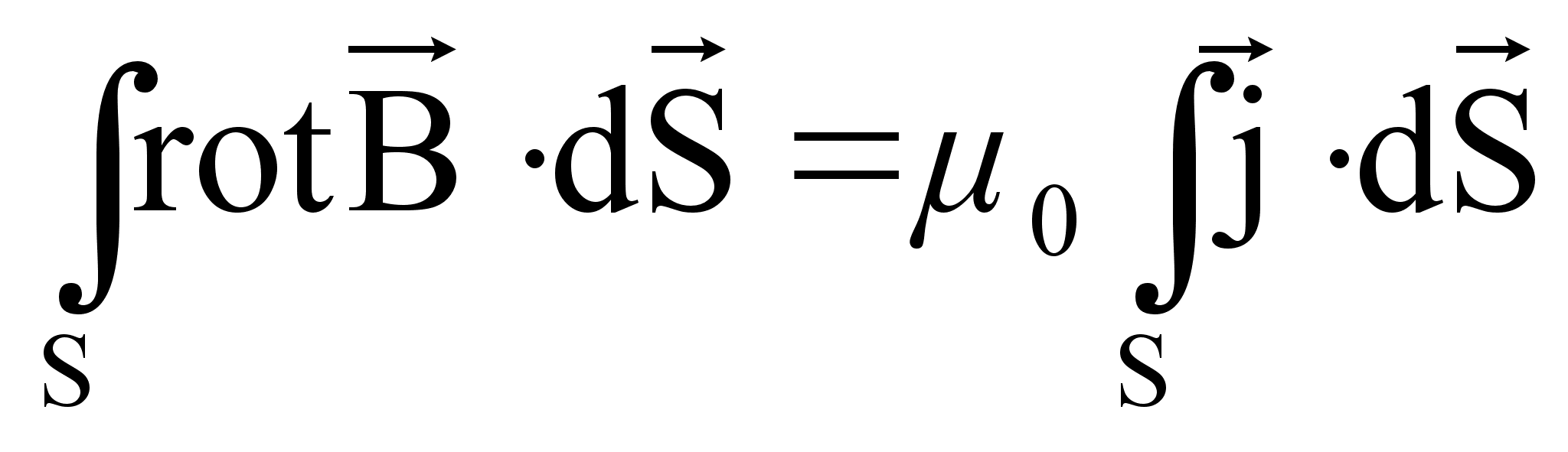
Интегралы равны, следовательно равны и подынтегральные выражения:
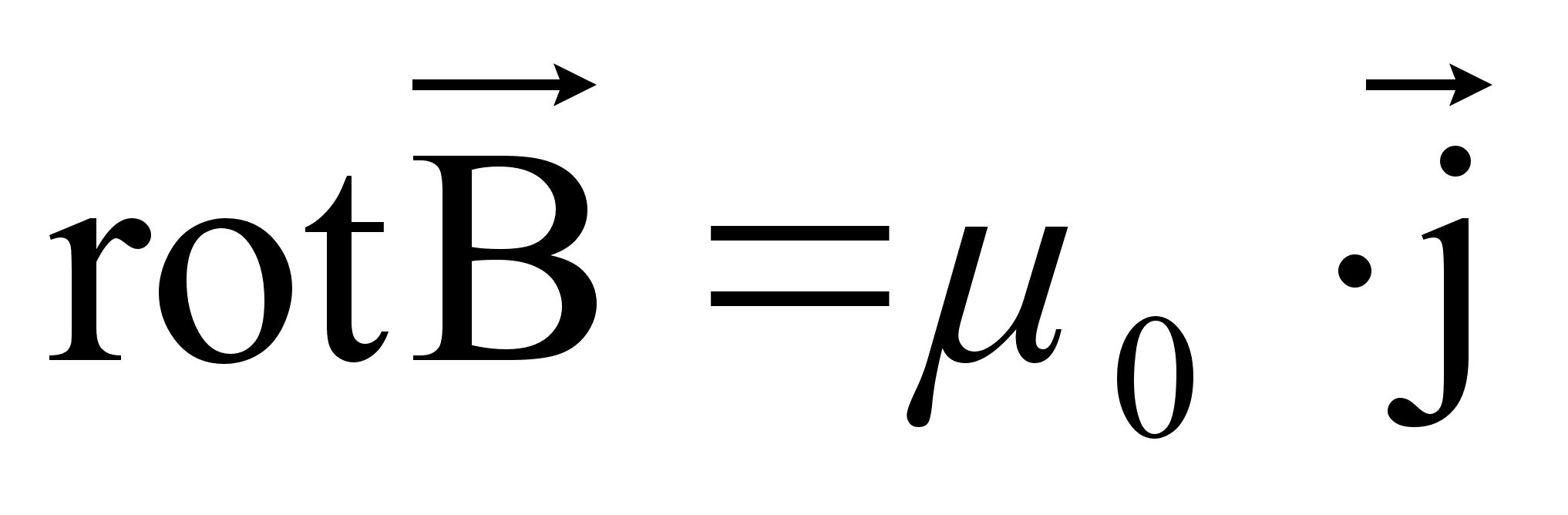 (75)
(75)
Таким образом, ротор вектора магнитной индукции пропорционален вектору плотности тока в данной точке.
Формула (75) справедлива для вакуума при отсутствии нестационарных электрический полей.
