Электромагнитные волны в волноводном тракте
Согласно теории де Бройля движущемуся электрону можно поставить в соответствие волновой процесс с длиной волны λ. Тогда для отбора стационарных круговых орбит в простейшей модели атома Бора необходимо выполнение следующего условия: длина окружности стационарной орбиты должна быть равна целому числу волн де Бройля. Иначе говоря, для устойчивых орбит должен иметь место резонанс бегущей волны, распространяющейся по замкнутому контуру. Этот вывод можно моделировать при помощи 3-см электромагнитных волн. Тот факт, что для бегущей волны, распространяющейся по замкнутому контуру, при соответствующем выборе длины контура действительно наблюдается явление резонанса, показано в работе (1) следующим образом (рис. 1).

Рисунок 1. Волноводное кольцо
Из отрезков 3-см волновода, разной формы собирается волноводное кольцо, в которое включены направленный ответвитель НО, 3-см измерительная линия ИЛ и диэлектрический фазовращатель φ. 3-см электромагнитные волны, модулированные по амплитуде низкой частотой (400 гц), поступают в кольцо от генератора Г, волноводный выход которого стыкован со входом направленного ответвителя. Диэлектрический фазовращатель позволяет менять электрическую длину контура. Детектор в зонде измерительной линии регистрирует амплитуду волны в данной точке контура. От зонда продетектированный сигнал через усилитель низкой частоты поступает на вход осциллографа ЭО-7.
Вначале фазовращатель стоит в нулевом положении. На экране осциллографа наблюдается сигнал небольшой амплитуды, так как при произвольной длине контура в нем не укладывается целое число волн и волны гасят друг друга. Вращая ручку фазовращателя, находят такое положение, что амплитуда сигнала проходит через максимальное значение. Это соответствует случаю, когда в кольце уложилось целое число волн. Можно убедиться, что в обоих случаях в контуре существует бегущая волна: при перемещении зонда вдоль линии изменения амплитуды сигнала незначительны. Они обусловлены неидеальной стыковкой деталей контура. Опыт показал, что при определенных условиях при бегущей волне имеет место резонанс.
Волноводное кольцо размыкается, удалив участок А В С, а открытые выходы волноводов замыкаются металлическими пластинками КК. В линии устанавливается стоячая волна. При перемещении зонда вдоль линии сигнал на экране осциллографа периодически меняется от нуля (узлы стоячей волны электрического поля) до максимума (пучности стоячей волны). Конечно, при показе этого опыта тщательно оговаривается различие природы волн де Бройля и электромагнитных и разъясняется, что задача опыта — лишь моделировать идеи де Бройля. (1). Однако эта оговорка ни в коей мере не отрицает полной аналогии между электрическими процессами, происходящими в электронной оболочке атома в стационарном либо квазистационарном состоянии, и поведением электромагнитной волны в замкнутой кольцевой системе при выполнении условия резонанса, так – как 1-й постулат Бора по форме полностью совпадает с условием резонанса электромагнитных волн в замкнутых системах. В настоящее время, несмотря на огромное количество работ, как теоретических, так и экспериментальных, в данном направлении, поведение волн во многом далеко от полноты своего описания. Это особенно ярко проявляется в случаях, когда длина волны является величиной, сравнимой с характерными размерами элементов систем. Таким процессом может быть рассеяние на спиральных элементах либо W - структурах, резонансные явления в волноводных и коаксиальных трактах.
Поведение электромагнитных полей в пространственно ограниченных системах зачастую представляет собой весьма сложный физический процесс, который не всегда даётся достаточно корректно описать при помощи математических выражений. Интерес к описанию этого процесса подтверждается тем, что в настоящее время в научной периодике имеется большое количество публикаций, посвященных описанию механизма самовозбуждения электромагнитной волны в замкнутых системах. Так, в работе (2) рассматривались вопросы о механизме появления комплексных волн в спектре экранированного волновода. С помощью теории преобразования типов волн объясняется механизм появления комплексных волн в спектре экранированного диэлектрического волновода. Для волновода круглой формы приведены результаты численных расчётов, подтверждающие правильность разработанной модели.
В работе (3) был предложен метод определения величины комплексной постоянной распространения поверхностной электромагнитной волны, не требующее знания электрофизических параметров исследуемого материала.
С точностью до членов размножения высшего порядка малости по степеням λ/L и Ω/ω, в работе (4) получены уравнения переноса энергии, импульса и момента импульса пакета электромагнитной волны, распространяющейся в слабопоглащающей однородной стационарной анизотропной и гиротропной среде с временной и пространственной дисперсией. Показано, что закон сохранения собственного момента импульса (спина) волны имеет место только для поперечных волн с круговой поляризацией. Определены выражения для плотности спина, его потока.
Сообщается (5) о новом подходе, позволяющем существенно эффективней и быстрее, а также с большей точностью решать задачи вычисления полей широкого класса диэлектрических волноводов. Этот подход при численной реализации обеспечивает хорошую устойчивость.
Метод интегрированного уравнения, полученный на основе применения тождества Грина, используется (6) для определения резонансных частот дисковых и кольцевых резонаторов, расположенные на однослойной диэлектрической подложке и заключенных в низкий цилиндрический резонатор- экран. Вследствие использования в качестве базисных функций собственных колебаний структуры существенно сокращено время расчетов. Приведены результаты определения резонансных частот дисковых резонаторов для колебаний типа Е010, ЕН110. В кольцевом резонаторе определены собственные частоты колебаний типа ЕН110, ЕН210, ЕН310.
Обсуждается вопрос о замене реальных граничных условий при решении задач отражения и прохождения электромагнитной волны через приближенными импедансными. (7)
Общая теория реактивной связи двух резонансных типов колебаний сформулирована (8) в терминах нормализованных эквивалентных сосредоточенных элементов. Выявлено влияние связи на добротность и уход резонансных частот.
Приведены результаты теоретических и экспериментальных исследований полосковых кольцевых резонаторов (9), перестраиваемые с помощью варакторных диодов. Кольца образованы щелевой линией передачи или компланарным волноводом. Получена (8) электронная перестройка резонансной частоты щелевого резонатора в полосе частот 3,03- 3,83 ГГц (23%) при вносимых потерях 4,5 ± 1,5 дБ, резонатор на копланарном волноводе перестраивается в полосе 2,83- 3,59 ГГц.
Рассматриваются (10) особенности прохождения плоской электромагнитной волны через бесконечную диэлектрическую среду, состоящую из плоскопараллельных пластин . Предполагается , что среда является периодической. Её периодические элементы состоят из конечного числа пластин с произвольными значениями диэлектрической проницаемости, волна падает под произвольным углом на пластины и имеет либо ТМ-, либо ТЕ- поляризацию. С использованием теоремы Флоке задача сводится к рассмотрению полей только в отдельном элементе периодичности среды. Метод демонстрируется на примере, когда элемент периодичности среды состоит только из двух пластин.
Предложена (11) схема возбуждения колебания кольцевого резонатора, использующая идею автоколебания и сохраняющая интегрирующий эффект. Автоколебания обеспечиваются внешней нелинейной запаздывающей обратной связью, связывающей колебания резонатора в некоторых точках с величиной напряжения на электродах в системе возбуждения колебаний. На основе известной нелинейной модели резонатора выявлены условия существования автоколебаний, исследована их устойчивость и получены асимптотические формулы. Показано отсутствие зависимости калибровочного коэффициента резонатора от коэффициента усиления в цепи внешней запаздывающей обратной связи.
Предложена (12) точная формула для расчёта числа типов волн, возбуждаемых в прямоугольном волноводе для произвольной полосы частот. Показано, что в пределе высоких частот полученная формула переходит в известное асимптотическое приближение. Проведено сравнение результатов расчёта числа типов волн по точной и асимптотической формулам.
Рассмотрено (13) применение конечно-разностных методов для расчёта диэлектрических волноведущих систем. Исследованы основные причины, препятствующие широкому использованию метода конечных разностей для расчёта открытых диэлектрических структур и волноводов с диэлектрическим наполнением. Указаны перспективные направления развития рассматриваемых методов.
В работе (14) излагается обзор современного состояния волноводной техники. Представлены частотные характеристики коэффициентов затухания в волноводах различных типов (круглых, прямоугольных, коаксиальных Н- образных). Дан также обзор конструкций устройств на волноводах с увеличенными размерами поперечного сечения: волноводных переходов, устройств для подавления волн высших типов .
В (15) даны результаты расчетов характеристик коэффициента затухания ряда типов волн в прямоугольных и круглых волноводах. Расчеты выполнены в приближении малых потерь. Результаты расчетов представлены в виде графиков зависимости нормированных коэффициентов затухания для 14 первых типов ТЕ и ТМ в прямоугольном волноводе и 15 в круглом от длины волны, нормированной к ширине прямоугольного волновода.
Изучены (16) общие закономерности формирования амплитудно-частотной характеристики симметричных волноводных или периодических резонаторов на основе выяснения их взаимосвязи с собственными частотами колебаний открытых структур. Исследовано влияние количества и местоположения собственных частот колебания одного или различных типов симметрии на частотные характеристики. Даны простые оценки зон наличия или отсутствия резонансов полного отражения и прохождения, добротности и величин смещения резонансов относительно реальных частей собственных частот.
При размерах систем сопоставимых с длиной волны излучения, распространяющихся в данной системе, проявляются квантовые эффекты, характерные для электромагнитных процессов происходящих в атомных и молекулярных системах для электромагнитных волн видимого диапазона, т.е. в оптике. В частности, поведение электрона в атоме водорода описывается на основе постулатов, т.е. утверждений, которые не могут быть доказаны, а воспринимаются как факт на основе экспериментальных результатов. Основным постулатом является утверждение о существовании стационарных орбит, на которых электрон не излучает, причем длина орбиты при этом равна длине волны электрона. Экспериментальную проверку данного постулата в оптике затруднительна, поскольку длина волны при этом весьма мала. Для радиотехнических систем, где длины волн имеют макроскопические размеры, постановка такого эксперимента вполне осуществима (16). Эксперимент по поведению бегущих электромагнитных волн в замкнутой системе, длина которой кратна длине волны, описан в литературе как демонстрационный, хотя изучение поведения бегущих волн в замкнутых системах представляет и чисто практический интерес.
В настоящей работе проведено экспериментальное исследование поведения бегущих электромагнитных волн в волноводном тракте. Целью настоящей работы являлось исследование частотной зависимости амплитуды бегущей электромагнитной волны в кольцевом волноводном тракте. Для этого необходимо было решить следующие задачи:
1) определить оптимальные условия возбуждения бегущей электромагнитной волны в кольцевом тракте;
2) исследовать процесс образования стоячей волны в кольцевом резонаторе и получить соответствующие частотные зависимости;
3) получить частотные зависимости для процесса интерференции бегущих волн в кольцевом резонаторе.
1. Общие сведения о волнах
1.1 Волновой процесс
Термины «волна», «волновой процесс», употребляемые в физике и технике, получили широкое распространение. Под распространением волны понимается постепенное вовлечение среды в некоторый физический процесс, приводящее к передаче энергии в пространстве.
Пусть в какой-то области пространства наблюдается физический процесс, который в точке ![]() можно охарактеризовать функцией
можно охарактеризовать функцией ![]() . В другой точке
. В другой точке ![]() измерения величины
измерения величины ![]() в это же время, быть может, покажут отсутствие процесса
в это же время, быть может, покажут отсутствие процесса![]() . Но через какое-то время он будет передан средой, и мы отметим, что
. Но через какое-то время он будет передан средой, и мы отметим, что ![]()
В простейшем случае будет обнаружено лишь запаздывание процесса во времени, т. е. ![]() , где
, где ![]() — время, требуемое для прохождения пути
— время, требуемое для прохождения пути ![]() со скоростью
со скоростью ![]() . Пусть в пространстве существует зависимость только от одной координаты
. Пусть в пространстве существует зависимость только от одной координаты ![]() . Характеризующая процесс функция
. Характеризующая процесс функция
![]() (1.1)
(1.1)
построена при ![]() и при
и при ![]() . Очевидно,
. Очевидно,![]()
![]() .
.
Говорят, что функция (1.1) описывает волну. Иногда волны этого рода называют «недеформируемыми»; имеется в виду, что временной закон во всех точках пространства — с точностью до сдвига ![]() — одинаков. Волна называется плоской и однородной. Дело в том, что, положив
— одинаков. Волна называется плоской и однородной. Дело в том, что, положив![]() , мы задаем плоскость, на которой мгновенное значение функции
, мы задаем плоскость, на которой мгновенное значение функции ![]() постоянно. Любую такую плоскость называют фронтом волны. В некоторый момент
постоянно. Любую такую плоскость называют фронтом волны. В некоторый момент ![]() фронт, для которого
фронт, для которого ![]() движется вдоль оси
движется вдоль оси ![]() со скоростью
со скоростью ![]() ,
,![]() . Плоскую однородную волну, распространяющуюся в противоположном направлении, следует описывать при помощи выражения (1.1) с изменением знака
. Плоскую однородную волну, распространяющуюся в противоположном направлении, следует описывать при помощи выражения (1.1) с изменением знака
![]() (1.1а)
(1.1а)
Обратимся к однородному волновому уравнению
![]() (1.2)
(1.2)
Если пользоваться декартовой системой координат ![]() и рассматривать только процессы, не зависящие от
и рассматривать только процессы, не зависящие от ![]() и
и ![]() , то волновое уравнение примет вид
, то волновое уравнение примет вид
![]() (1.3)
(1.3)
Путем непосредственной подстановки нетрудно убедиться, что функции, выражаемые формулами (1.1) и (1.1а), являются решениями одномерного волнового уравнения (1.3).
Общее решение уравнения (1.3) выражает формула
![]() (1.4)
(1.4)
где ![]() и
и ![]() — произвольные дважды дифференцируемые функции. Это наложение двух плоских однородных недеформируемых: волн, распространяющихся в противоположных направлениях.
— произвольные дважды дифференцируемые функции. Это наложение двух плоских однородных недеформируемых: волн, распространяющихся в противоположных направлениях.
1.2 Гармонические волны
Если в (1.1) взять такую функцию![]() , что
, что ![]() то в каждой точке пространства процесс будет иметь характер гармонических колебаний
то в каждой точке пространства процесс будет иметь характер гармонических колебаний
![]()
или
![]()
![]() (1.5)
(1.5)
Такого рода плоская однородная волна называется гармонической, а введенный параметр ![]() — волновым числом.
— волновым числом.
Как видно, полная фаза гармонических колебании в пространстве ![]() при заданном
при заданном ![]() убывает пропорционально
убывает пропорционально ![]() ; значения функции
; значения функции ![]() при этом периодически повторяются. Пространственный период называют длиной волны. Очевидно, для произвольного
при этом периодически повторяются. Пространственный период называют длиной волны. Очевидно, для произвольного ![]() должно быть
должно быть ![]()
![]() . Поэтому из (1.5) следует, что
. Поэтому из (1.5) следует, что ![]() , т. е.
, т. е.
![]() (1.6)
(1.6)
а также
![]() (1.7)
(1.7)
где ![]() —частота процесса.
—частота процесса.
Чтобы составить, более наглядное представление о гармонической волне, положим сначала ![]() и получим
и получим ![]() т.е. функцию, характеризующую распределение величины
т.е. функцию, характеризующую распределение величины ![]() вдоль оси
вдоль оси ![]() в начальный момент
в начальный момент ![]() . Эта косинусоида (кривая на рис. 1.2а) представляет собой как бы «мгновенный снимок» процесса. Выберем следующий фиксированный момент
. Эта косинусоида (кривая на рис. 1.2а) представляет собой как бы «мгновенный снимок» процесса. Выберем следующий фиксированный момент ![]() и для него запишем
и для него запишем
![]()
где ![]() то есть не что иное, как расстояние, пройденное волной за истекшее время
то есть не что иное, как расстояние, пройденное волной за истекшее время ![]() . «Мгновенный снимок», соответствующий моменту
. «Мгновенный снимок», соответствующий моменту ![]() , дает, таким образом, косинусоиду, смещенную по оси
, дает, таким образом, косинусоиду, смещенную по оси ![]() на расстояние
на расстояние ![]() (кривая 2 на рис. 1.2а). Итак, распространение гармонической волны — это движение косинусоидального распределения и вдоль прямой с постоянной скоростью.
(кривая 2 на рис. 1.2а). Итак, распространение гармонической волны — это движение косинусоидального распределения и вдоль прямой с постоянной скоростью.
Плоская однородная гармоническая волна выражается одним из частных решений одномерного волнового уравнения (1.3). Метод комплексных амплитуд приводит (1.3) к виду
![]()
![]() (1.8)
(1.8)
Это не что иное, как одномерная форма уравнения Гельмгольца. Его общее решение можно выразить следующей суммой:
![]() (1.9)
(1.9)
(![]() и
и ![]() —комплексные константы:
—комплексные константы: ![]() и
и ![]() ).
).
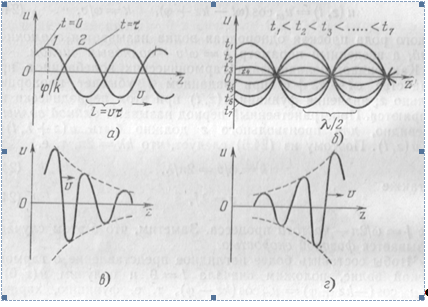
Рисунок 1.2
Умножая комплексную амплитуду ![]() на
на ![]() и отделяя вещественную часть, находим
и отделяя вещественную часть, находим
![]() (1.10)
(1.10)
Это наложение двух гармонических волн, распространяющихся в противоположных направлениях. Гармоническая волна, движущаяся вдоль оси ![]() , возникает как частное решение при
, возникает как частное решение при![]() .
.
В качестве другого частного решения рассмотрим наложение бегущих навстречу волн с одинаковыми амплитудами ![]() и начальными фазами
и начальными фазами ![]() . При этом из (1.10) получаем
. При этом из (1.10) получаем
![]() (1.11)
(1.11)
Такой процесс называется стоячей волной. Его отличительной особенностью является синфазность колебаний. Действительно, в каждой области постоянства знака множителя ![]() фаза зависит только от времени (это величина
фаза зависит только от времени (это величина ![]() или
или ![]() ). В зависимости от
). В зависимости от ![]() косинусоидального изменяется амплитуда гармонических колебаний
косинусоидального изменяется амплитуда гармонических колебаний ![]() . Ряд «мгновенных снимков» процесса для разных моментов времени дает картину, показанную на рис. 1.2б; косинусоидальное распределение и вдоль оси
. Ряд «мгновенных снимков» процесса для разных моментов времени дает картину, показанную на рис. 1.2б; косинусоидальное распределение и вдоль оси ![]() не движется (в отличие от бегущей волны), а испытывает «пульсации». При этом расстояния между соседними неподвижными нулями (узлами) равны
не движется (в отличие от бегущей волны), а испытывает «пульсации». При этом расстояния между соседними неподвижными нулями (узлами) равны ![]() ; таковы же и расстояния между соседними максимумами (пучностями).
; таковы же и расстояния между соседними максимумами (пучностями).
1.3 Поляризация и наложение волн
Для описания ориентации волны, распространяющейся в заданном направлении, существует понятие поляризации. Плоскостью поляризации называют плоскость, проходящую через направление распространения и параллельную вектору ![]() . Таким образом, всякое наложение двух волн с произвольными амплитудами и фазами есть также некоторая электромагнитная волна. Любая из плоскостей, проходящих через ось
. Таким образом, всякое наложение двух волн с произвольными амплитудами и фазами есть также некоторая электромагнитная волна. Любая из плоскостей, проходящих через ось ![]() , может в равной мере быть плоскостью поляризации.
, может в равной мере быть плоскостью поляризации.
Существенно, что при распространении волны плоскость ее поляризации может и не оставаться неподвижной, т. е. волна может изменять свою ориентацию относительно направления распространения. Действительно, рассмотрим электрические поля двух ортогонально поляризованных волн одного направления и составим их наложение
![]() (1.22)
(1.22)
Если фазы волн совпадают (![]() и
и ![]() ), то, как легко убедиться, наложение волн есть волна, поляризованная в неподвижной плоскости, составляющей угол
), то, как легко убедиться, наложение волн есть волна, поляризованная в неподвижной плоскости, составляющей угол ![]() с плоскостью поляризации первой волны. Это плоская, или линейная, поляризация.
с плоскостью поляризации первой волны. Это плоская, или линейная, поляризация.
Картина оказывается иной, если фазы налагающихся волн различны. Пусть, например, при одинаковых амплитудах (![]() ) фазовое различие составляет
) фазовое различие составляет ![]() . Полагая в (1.22)
. Полагая в (1.22) ![]() и
и ![]() , определим вектор
, определим вектор ![]() как
как ![]()
![]() (1.23)
(1.23)
Определяя угол ![]() , указывающий положение плоскости поляризации волны, имеем
, указывающий положение плоскости поляризации волны, имеем
![]() (1.24)
(1.24)
т. е. угол наклона вектора ![]() к оси
к оси ![]() не остается постоянным в пространстве и времени, а равен
не остается постоянным в пространстве и времени, а равен ![]() . Как видно, в каждой фиксированной плоскости
. Как видно, в каждой фиксированной плоскости ![]() вектор
вектор ![]() вращается с угловой скоростью
вращается с угловой скоростью ![]() , а в фиксированный момент времени
, а в фиксированный момент времени ![]() распределение поля вдоль оси таково, что конец вектора
распределение поля вдоль оси таково, что конец вектора ![]() «скользит по винтовой линии». Это волна круговой поляризации, точнее, левой круговой поляризации. Правая круговая поляризация соответствует случаю
«скользит по винтовой линии». Это волна круговой поляризации, точнее, левой круговой поляризации. Правая круговая поляризация соответствует случаю ![]() и
и ![]() (вращение в противоположном направлении).
(вращение в противоположном направлении).
Если налагаемые волны имеют произвольные амплитуды и фазы, то результирующий волновой процесс есть волна эллиптической поляризации. Вращаясь, вектор ![]() при этом изменяется по величине и описывает эллипс. Ориентация и эксцентриситет эллипса определяются соотношением комплексных чисел
при этом изменяется по величине и описывает эллипс. Ориентация и эксцентриситет эллипса определяются соотношением комплексных чисел ![]() и
и ![]() .
.
Наложение противоположно направленных волн одинаковых амплитуд вызывает процесс, называемый стоячей волной. Особенностью электромагнитной стоячей волны является характерное пространственное и фазовое смещение распределений ![]() и
и ![]() .
.
Рассмотрим, например, стоячую волну, поляризованную в плоскости ![]() , Положив
, Положив ![]() и
и ![]() находим
находим
 (1.25)
(1.25)
или, переходя от комплексных амплитуд к векторам поля в случае идеального диэлектрика (![]() ,
, ![]() ):
):
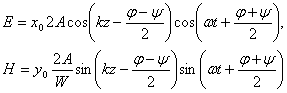 (1.26)
(1.26)
Узлы (или пучности) стоячих волн векторов ![]() и
и ![]() сдвинуты на четверть волны. Во времени же эти поля смещены на
сдвинуты на четверть волны. Во времени же эти поля смещены на ![]() по фазе. Такая стоячая волна в среднем не переносит энергии, как легко убедиться, вычисляя среднюю величину вектора Пойнтинга.
по фазе. Такая стоячая волна в среднем не переносит энергии, как легко убедиться, вычисляя среднюю величину вектора Пойнтинга.
2. Резонансы и направляемые волны в плоских системах
2.1 Плоский резонатор
Распределение поля, возникающее в идеальном диэлектрике при нормальном падении волны на идеально проводящую плоскость, стоячая волна обладает тем свойством, что в любой плоскости, расположенной на расстоянии ![]()
![]() от границы раздела сред, выполняется условие
от границы раздела сред, выполняется условие ![]() . Следовательно любую из таких плоскостей можно заменить границей с идеальным проводником, так что в «отсеченном» диэлектрическом слое сможет существовать прежнее поле.
. Следовательно любую из таких плоскостей можно заменить границей с идеальным проводником, так что в «отсеченном» диэлектрическом слое сможет существовать прежнее поле.
Рассмотрим теперь плоский диэлектрический слой между двумя идеально проводящими плоскостями, расположенными на некотором фиксированном расстоянии ![]() . Из предыдущего следует, что необходимым условием существования поля в данной системе является кратность величины
. Из предыдущего следует, что необходимым условием существования поля в данной системе является кратность величины ![]() половине длины волны в диэлектрике. Запишем это в двух формах:
половине длины волны в диэлектрике. Запишем это в двух формах:
![]() ,
, ![]()
![]() (2.1)
(2.1)
Как видно равенство (2.1) порождает бесконечную последовательность «разрешенных» длин волн ![]() и соответствующих волновых чисел
и соответствующих волновых чисел ![]() , при которых в слое могут существовать свободные поля вполне определенной структуры. Из (2.1) нетрудно найти круговые частоты
, при которых в слое могут существовать свободные поля вполне определенной структуры. Из (2.1) нетрудно найти круговые частоты ![]() соответствующие волновым числам
соответствующие волновым числам ![]() :
:
![]()
![]() (2.2)
(2.2)
Говорят, что электродинамической системе свойственны собственные колебания, а величины ![]() называются ее собственными круговыми частотами.
называются ее собственными круговыми частотами.
Полагая ![]() и
и ![]() в (2.2) комплексными и используя представления
в (2.2) комплексными и используя представления ![]() ,
, ![]() , убеждаемся, что собственные частоты существуют и оказываются комплексными:
, убеждаемся, что собственные частоты существуют и оказываются комплексными:
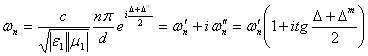 (2.3)
(2.3)
Рассмотренная система есть простейший электромагнитный резонатор. При внешнем возбуждении с частотой ![]() в экранированном слое будут происходить так называемые вынужденные колебания поля, амплитуда которых каждый раз резко возрастает при
в экранированном слое будут происходить так называемые вынужденные колебания поля, амплитуда которых каждый раз резко возрастает при ![]()
![]() . Это и есть резонансы поля в слое.
. Это и есть резонансы поля в слое.
2.2 Резонансные системы на основе отрезков однородной линии
В коротковолновой части метрового диапазона волн, а также в длинноволновой части дециметрового диапазона (примерно до частоты 1000 МГц) для создания PC ламповых генераторов применяют индуктивные короткозамкнутые отрезки двухпроводных симметричных линий. Проводники линий возбуждаются в противофазе, структура электромагнитного поля в линии соответствует Т-волне. Так как такие PC симметричны электрически, их удобно использовать в двухтактных генераторах. Концы проводников, образующих двухпроводную линию, соединяют между собой неподвижной жесткой перемычкой, через которую к анодам ламп подключают источник анодного напряжения
В однотактных генераторах можно использовать однопроводные линии — проводник над заземленной плоскостью а также симметричные или несимметричные полосковые линии.
В генераторах на лампах с кольцевыми или дисковыми выводами электродов наиболее целесообразно использовать отрезки коаксиальных линий. Для уменьшения их длины в ряде случаев применяют центральный проводник линии в виде спирали.
Рассмотрим порядок расчета PC, выполненных на основе отрезков короткозамкнутых однородных линий. Исходными данными являются: длина волны λ, или диапазон длин волн λmax и λmin; значение сосредоточенной емкости С0, включенной в начале линии; конструкция, габариты генераторного прибора; форма и размеры выводов его электродов (эти данные вместе с длиной волны определяют выбор типа линии) (22).
Диаметр проводников двухпроводной линии выбирают равным или близким к диаметру соответствующего вывода электрода. Диаметры проводников коаксиальной линии определяются диаметрами кольцевых выводов металлокерамических ламп.
1. Выбирают волновое сопротивление линии и рассчитывают ее геометрические размеры в поперечном сечении по соотношениям (23). Выбор волнового сопротивления в известной степени определяет добротность PC и ее электрическую прочность.
Максимальная собственная добротность коаксиальной линии имеет место при отношении диаметров проводников D/d = 3,6, что соответствует волновому сопротивлению Z0 = 77 Ом, причем при изменении D/d от 2,5 до 5 собственная добротность линии меняется мало.
При постоянном погонном сопротивлении линии R1 потери в проводнике падают при уменьшении амплитуды СВЧ- тока, протекающего через него. С этой точки зрения следует увеличивать волновое сопротивление линии. Но так как по конструктивным соображениям диаметр наружного проводника коаксиальной линии или расстояние между проводниками двухпроводной линии не должны быть чрезмерно большими, то волновое сопротивление увеличивают за счет уменьшения диаметра внутреннего проводника коаксиальной линии или диаметров проводников двухпроводной. Однако при этом растет R1 и увеличиваются потери в линии. Рекомендуется поэтому выбирать волновое сопротивление коаксиальных линий в пределах 30—70 Ом, а двухпроводных 200—400 Ом.
2. По заданным значениям емкости С0 и диапазона длин волн λmin — λmax при условии, что перестройка PC выполняется перемещением короткозамыкателя, определяют минимальную и максимальную длину линии с использованием найденного значения Z0. Как правило, предусматривают работу системы на основном виде колебаний, т. е. с n = 0.
3. По формулам (22) рассчитывают погонные параметры R1,C1, L1, которые определяют значения элементов схемы замещения линии, приведенной на рис. 2.3. Погонная проводимость линии G1 при ее заполнении воздухом пренебрежимо мала. Длина каждой ячейки l1 равна принятой единице длины, например 1 см.

Рисунок 2.1 Схема замещения линии
4. Определяют эквивалентное резонансное сопротивление ненагруженной PC (на холостом ходу). При этом R0э, Rxx рассматривают как образованное параллельным соединением двух эквивалентных сопротивлений: собственно линии Rэл и генератора Rэг. Таким образом R0э,Rхх = Rэг Rэл/ (Rэг+ Rэл).
Эквивалентное сопротивление генератора определяется потерями внутри генераторного прибора: в диэлектриках, электродах (за счет их поверхностного сопротивления) и т. д. Полный учет этих потерь чрезвычайно сложен, однако в первом приближении можно считать, что Rэг ≈(1,0÷1,5)Rэл. Потери в генераторном приборе с ростом частоты возрастают, наименьшее значение Rэг соответствует коротковолновой части дециметрового диапазона волн, наибольшее — длинноволновой.
Эквивалентное сопротивление линии Rэл, в свою очередь рассматривают (22) как параллельное соединение двух сопротивлений R’эл и R”эл, соответствующих потерям в проводниках линии и в переходном сопротивлении между проводниками и короткозамыкающим элементом.
5. Характеристическое сопротивление эквивалентного контура ρэ = 1/(ω0Сэ) определяется емкостью эквивалентного контура Сэ = С0 + Сэл, где Сэл — эквивалентная емкость отрезка линии — может быть найдена из условия равенства электрической энергии, запасаемой в этой емкости за период СВЧ- колебаний, и энергии, запасаемой в распределенной емкости отрезка линии длиной l:
На основном виде колебаний Сэ может быть рассчитана по соотношению
Сэ = Со (2.4)
(2.4)
2.3 Резонансные системы с отрезками линий, содержащими неоднородности
В ряде случаев по конструктивным соображениям, а также, например, для улучшения фильтрующих свойств, расширения диапазона перестройки PC в качестве составной части PC используют ступенчато-неоднородные отрезки линий. Коаксиальная линия может состоять из нескольких отрезков, имеющих разные диаметры внутренних и внешних проводников, т. е. обладающих разными значениями волновых сопротивлений; могут быть изменены размеры двухпроводной или полосковой линии и т. д. Эти неоднородности приводят к возбуждению высших типов волн, локализованных вблизи неоднородности. Поля таких волн имеют в основном реактивный характер, поэтому поглощением мощности, связанным с их возбуждением, в первом приближении можно пренебречь. Неоднородность может быть учтена включением в эквивалентную схему линии некоторой реактивной проводимости. Скачкообразные изменения размеров проводников линии учитывают включением сосредоточенной емкости.
Резонансное условие для сложной PC, состоящей из параллельно включенных участков линий, записывается для выбранного сечения в виде равенства нулю суммы реактивных проводимостей, определяемых пересчетом к этому сечению проводимостей отдельных участков: Yвх1 + Yн + Yвх2 = 0,- где Yн = jCн /(5,31λ) -проводимость емкости, отражающей в эквивалентной схеме неоднородность линии; Yвх2=-j/(Z02tg(2πl2λ)) — входая проводимость короткозамкнутого отрезка линии длиной l1; Yвх1 =-j/Xвх1; Xвх1 — входное реактивное сопротивление участка линии длиной l1, нагруженного на конце сосредоточенной емкостью С0.
Полосы пропускания PC располагаются в окрестности каждого значения резонансной частоты. Ширина полос пропускания определяется нагруженной добротностью эквивалентного контура на соответствующем виде колебаний.
Для выполнения требований по фильтрации высших гармоник, всегда присутствующих в спектре СВЧ- тока генератора, необходимо, чтобы резонансные частоты ω0, ω1, ω2, ... не были бы кратными.
Если аналогичным образом найти резонансные частоты PC с короткозамкнутым отрезком однородной линии (см. рис.2.2), то окажется, что PC, образованные из отрезков однородной линии, обладают низкими фильтрующими свойствами для нечетных гармоник.
Когда трудно получить одновременно большое значение R0э.хх при перестройке PC в широком диапазоне частот, линейный закон перестройки, хорошие фильтрующие свойства и т. д., в PC включают отрезки плавно-неоднородных линий. В них волновое сопротивление вдоль линий изменяется по определенному закону, для чего в двухпроводных линиях обычно изменяют расстояние между проводниками линии; в коаксиальных — диаметры проводников (чаще всего наружного); в полосковых — ширину полоскового проводника.
К плавно-неоднородным линиям относят и радиальную линию, у которой с увеличением радиуса растет погонная емкость, а погонная индуктивность и волновое сопротивление уменьшаются. Для таких линий
Z0 (r) = 60h/r = Z0r0/r, (2.5)
где Z0 — волновое сопротивление в начале линии, на начальном радиусе r0; Z0 (r) — волновое сопротивление на некотором текущем радиусе r. Радиальные линии обычно возбуждают электрическим полем в емкостном зазоре d, диаметр которого 2r0.

Рисунок 2.2 Радиальная линия (а) и распределение в ней амплитуд напряжения и тока (б)
Условие резонанса (для начала радиальной линии, r=r0)
jC0Z0/(5,31l) + Y(r0,R) (2.6)
Первый член выражения (2.6) является нормированной по Z0 проводимостью емкостного зазора, второй член — нормированной входной проводимостью радиальной линии, короткозамкнутой на радиусе r = R. Расчет такой PC производится по уравнению (2.6), при этом обычно задают значения С0, λ, r0, h. Если емкость С0
