* Алгебры и их применение
Пусть Н – гильбертово пространство, L(Н) – множество непрерывных линейных операторов в Н. Рассмотрим подмножество А в L(Н), сохраняющееся при сложении, умножении, умножении на скаляры и сопряжении. Тогда А – операторная *-алгебра. Если дана абстрактная *-алгебра А, то одна из основных задач теории линейных представлений (*-гомоморфизмов А в L(Н)) – перечислить все ее неприводимые представления (с точностью до эквивалентности).
Теория унитарных представлений РіСЂСѓРїРї РІРѕСЃС…РѕРґРёС‚ Рє XIX веку Рё связана СЃ именами Р“.Фробениуса, Р.РЁСѓСЂР°, Р’.Бернсайда, Р¤.Р. Молина Рё РґСЂ. Р’ СЃРІСЏР·Рё СЃ предложениями Рє квантовой физике теория унитарных представлений топологических РіСЂСѓРїРї, РіСЂСѓРїРї Ли, РЎ*-алгебр была разработана Р.Рњ.Гельфандом, Рњ.Рђ. Наймарком, Р.Сигалом, Р–.Диксмье, Рђ.Рђ. Кирилловым Рё РґСЂ. РІ 60-70-С… годах XX века. Р’ дальнейшем интенсивно развивается теория представлений *-алгебр, заданных образующими Рё соотношениями.
Дипломная работа посвящена развитию теории представлений (конечномерных и бесконечномерных) *-алгебр, порожденных двумя проекторами.
Глава I в краткой форме содержит необходимые для дальнейшего сведения из теории представлений и функционального анализа. В §1 дано определение *-алгебры и приведены простейшие свойства этих алгебр. В §2 излагаются основные свойства представлений, вводятся следующие понятия: неприводимость, эквивалентность, прямая сумма, интегрирование и дезинтегрирование представлений. В §3 определяются тензорные произведения пространств, тензорные произведения операторов и др. (см. (2), (3), (4), (8), (9))
В Главе II изучаются представления *-алгебры P2
P2 = РЎ < p1, p2 | p12 = p1* = p1, p22 = p2* = p2 >,
порожденной двумя самосопряженными идемпотентами, то есть проекторами (см., например, (12)). Найдены все неприводимые *-представления *-алгебры P2, с точностью до эквивалентности., доказаны соответствующие спектральные теоремы.
Р’ В§1 рассматриваются только конечномерные *-представления π РІ унитарном пространстве Рќ. Описаны РІСЃРµ неприводимые Рё неэквивалентные *-представления *-алгебры P2 . Неприводимые *-представления P2 одномерны Рё двумерны:
4 одномерных: π0,0(p1) = 0, π0,0(p2) = 0; π0,1(p1) = 0, π0,1(p2) = 1;
π1,0(p1) = 1, π1,0(p2) = 0; π1,1(p1) = 1, π1,1(p2) = 1.
Рдвумерные: ![]() ,
, 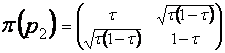 τ
τ ![]() (0, 1).
(0, 1).
Доказана спектральная теорема Рѕ разложении пространства Рќ РІ ортогональную СЃСѓРјРјСѓ инвариантных относительно π подпространств Рќ, Р° также получено разложение π РЅР° неприводимые *-представления. Результаты В§1 относятся Рє математическому фольклору.
В §2 получены основные результаты работы. Для пары проекторов в сепарабельном гильбертовом пространстве Н приведено описание всех неприводимых представлений, доказана спектральная теорема.
В Главе III спектральная теорема для пары проекторов Р1, Р2, применяется к изучению сумм Р1+Р2, аР1+bР2 (0 < a < b). Получены необходимое и достаточное условие на самосопряженный оператор А для того чтобы А = Р1+Р2 или А = аР1+bР2, 0 < a < b, (этот частный случай задачи Г.Вейля (1912 г.) о спектре суммы пары самосопряженных операторов).
Глава I. Основные понятия и определения
§ 1. ![]() - алгебры
- алгебры
Определение ![]() - алгебры.
- алгебры.
Определение 1.1. Совокупность А элементов x, y, … называется алгеб- рой, если:
А есть линейное пространство;
в А введена операция умножения (вообще некоммутативного), удовлет- воряющая следующим условиям:
α (x y) = (α x) y,
x (α y) = α (x y),
(x y) z = x (y z),
(x + y) = xz +xy,
x (y + z) = xy + xz для любых x, y, z ![]() Рђ Рё любых чисел α.
Рђ Рё любых чисел α.
Два элемента x, y алгебры А называются перестановочными, если xy = yx. Алгебра А называется коммутативной, если все ее элементы попарно пере- становочны.
Определение 1.2. Пусть Рђ – алгебра над полем РЎ комплексных чисел. Рнволюцией РІ Рђ называется такое отображение x → x* алгебры Рђ РІ Рђ, что
(x*)* = x;
(x + y)* = x* + y*;
(α x)* = ![]() x*;
x*;
(x y)* = y*x* для любых x, y ![]() С.
РЎ.
Алгебра над РЎ, снабженная инволюцией, называется инволютивной алгеброй или *- алгеброй. Рлемент С…* называют сопряженным Рє С…. Подмножество Рђ, сохраняющееся РїСЂРё инволюции, называется само- сопряженным.
РР· свойства (i) следует, что инволюция РІ Рђ необходимо является биекцией Рђ РЅР° Рђ.
1.2. Примеры
РќР° Рђ = РЎ отображение z →![]() (комплексное число, сопряженное Рє z) есть инволюция, превращающая РЎ РІ коммутативную *- алгебру.
(комплексное число, сопряженное к z) есть инволюция, превращающая С в коммутативную *- алгебру.
Пусть Рў – локально компактное пространство, Рђ = РЎ(Рў) – алгебра непре- рывных комплексных функций РЅР° Рў, стремящихся Рє нулю РЅР° бесконечности (то есть для любого ε > 0 множество {t![]() T: |f (t)|
T: |f (t)| ![]() ε} компактно, f (t)
ε} компактно, f (t) ![]() Рђ. Снабжая Рђ отображением f→
Рђ. Снабжая Рђ отображением f→![]() получаем коммутативную *- алгебру. Если Рў сводится Рє РѕРґРЅРѕР№ точке, то возвращаемся Рє примеру 1).
получаем коммутативную *- алгебру. Если Т сводится к одной точке, то возвращаемся к примеру 1).
Пусть Н – гильбертово пространство. А = L(H) – алгебра ограниченных линейных операторов в Н. Зададим инволюцию как переход к сопряженному оператору. Тогда А - *- алгебра.
Обозначим через Рљ(Рќ) совокупность всех компактных операторов РІ гильбертовом пространстве Рќ; операции сложения, умножения РЅР° число Рё умножения определим как соответствующие действия СЃ операторами. РўРѕРіРґР° Рљ(Рќ) будет *- алгеброй, если ввести инволюцию Рђ→Рђ* (Рђ![]() Рљ(Рќ)). Алгебра Рљ(Рќ) РІ случае бесконечного Рќ есть алгебра без единицы. Действительно, если единичный оператор I принадлежит Рљ(Рќ), то РѕРЅ переводит открытый единичный шар S
К(Н)). Алгебра К(Н) в случае бесконечного Н есть алгебра без единицы. Действительно, если единичный оператор I принадлежит К(Н), то он переводит открытый единичный шар S![]() H в себя. Значит I не может быть компактным оператором.
H в себя. Значит I не может быть компактным оператором.
Обозначим через W совокупность всех абсолютно сходящихся рядов ![]() .
.
Алгебра W есть *- алгебра, если положить ![]() . (
. (![]() )
)
1.3. Алгебры с единицей
Определение 1.3. Алгебра А называется алгеброй с единицей, если А содержит элемент е, удовлетворяющий условию
ех = хе = х для всех х![]() А (1.1.)
Рђ (1.1.)
Рлемент Рµ называют единицей алгебры Рђ.
Теорема 1.1. Алгебра А не может иметь больше одной единицы.
Доказательство. Действительно, если Рµ΄ - также единица РІ Рђ, то
Рµ΄С… = С…Рµ΄ = С…, для всех С…![]() Рђ (1.2.)
Рђ (1.2.)
Полагая РІ (1.1.) С… = Рµ΄, Р° РІ (1.2.) С… = Рµ, получим:
ее΄ = Рµ΄Рµ = Рµ΄ Рё Рµ΄Рµ = ее΄ =Рµ, следовательно Рµ΄ = Рµ.
Теорема 1.2. Р’СЃСЏРєСѓСЋ алгебру Рђ без единицы можно рассматривать как подалгебру некоторой алгебры Рђ΄ СЃ единицей.
 Доказательство. Рскомая алгебра должна содержать РІСЃРµ СЃСѓРјРјС‹ С…΄=αРµ + С…, С…
Доказательство. Рскомая алгебра должна содержать РІСЃРµ СЃСѓРјРјС‹ С…΄=αРµ + С…, С…![]() Рђ; СЃ РґСЂСѓРіРѕР№ стороны, совокупность всех таких СЃСѓРјРј образует алгебру Рђ΄, РІ которой основные операции определяются формулами:
Рђ; СЃ РґСЂСѓРіРѕР№ стороны, совокупность всех таких СЃСѓРјРј образует алгебру Рђ΄, РІ которой основные операции определяются формулами:
β(αРµ + С…) = βαРµ + βС…, (α1Рµ + С…1) + (α2Рµ + С…2) = (α1 + α2)Рµ + (С…1 + С…2),
(α1 Рµ + С…1)(α2 Рµ+ С…2 )=α1 α2 Рµ +α1 С…2 +α2 С…1 + С…1 С…2 (1.3.)
Каждый элемент С…΄ РёР· Рђ΄ представляется единственным образом РІ РІРёРґРµ
С…΄ = αРµ + С…, С…![]() Рђ, так как РїРѕ условию Рђ РЅРµ содержит единицы. Поэтому Рђ΄ можно реализовать как совокупность всех формальных СЃСѓРјРј С…΄ = αРµ + С…, С…
Рђ, так как РїРѕ условию Рђ РЅРµ содержит единицы. Поэтому Рђ΄ можно реализовать как совокупность всех формальных СЃСѓРјРј С…΄ = αРµ + С…, С…![]() Рђ, РІ которой основные операции определяются формулами (1.3.); сама алгебра Рђ получится РїСЂРё α = 0.
Рђ, РІ которой основные операции определяются формулами (1.3.); сама алгебра Рђ получится РїСЂРё α = 0.
 Алгебру Рђ΄ можно также реализовать как совокупность всех пар (α, С…), С…
Алгебру Рђ΄ можно также реализовать как совокупность всех пар (α, С…), С…![]() Рђ, РІ которой основные операции определяются РїРѕ формулам:
А, в которой основные операции определяются по формулам:
β (α, С…) = (βα, βС…), (α1, С…1) + (α2, С…2) = (α1 + α2, С…1 + С…2),
(α1, С…1)(α2, С…2) = (α1α2, α1С…2 + α2 С…1 + С…1С…2), (1.4.)
аналогично тому, как определяются комплексные числа. Саму алгебру А можно тогда рассматривать как совокупность всех пар (0, х), х![]() А и не делать различия между х и (0, х). Полагая е = (0, х), мы получим:
А и не делать различия между х и (0, х). Полагая е = (0, х), мы получим:
(α, С…) = α(1, 0) + (0, С…) = αРµ + С…,
так что вторая реализация алгебры Рђ΄ равносильна первой.
Переход РѕС‚ Рђ Рє Рђ΄ называется присоединением единицы.
Определение 1.4. Рлемент y называется левым обратным элемента С…, если xy = e. Рлемент z называется правым обратным элемента С…, если xz = e.
Если элемент х имеет и левый, и правый обратные, то все левые и правые обратные элемента х совпадают. Действительно, умножая обе части равенства yx = e справа на z, получим
z = (yx)z = y(xz) = ye,
В этом случае говорят, что существует обратный х-1 элемента х.
1.4. Простейшие свойства ![]() - алгебр
- алгебр
Определение 1.5. Рлемент С… *-алгебры Рђ называется эрмитовым или самосопряженным, если С…* = С…, нормальным, если С…С…* = С…*С…. Рдемпотентный эрмитов элемент называется проектором. Рлемент алгебры называется идемпотентным, если РІСЃРµ его (натуральные) степени совпадают.
Каждый эрмитов элемент нормален. Множество эрмитовых элементов есть вещественное векторное подпространство А. Если х и y эрмитовы, то (xy)*= y*x* = yx; следовательно, xy эрмитов, если x и y перестановочны. Для каждого х![]() А элементы хх* и х*х эрмитовы. Но, вообще говоря, эрмитов элемент не всегда представим в этом виде, как показывает пример 1 из пункта 1.2. Действительно, для любого z
А элементы хх* и х*х эрмитовы. Но, вообще говоря, эрмитов элемент не всегда представим в этом виде, как показывает пример 1 из пункта 1.2. Действительно, для любого z![]() C
C ![]() , но если z действительно отрицательное число, то его нельзя представить в виде
, но если z действительно отрицательное число, то его нельзя представить в виде ![]() .
.
Теорема 1.3. Всякий элемент х *-алгебры А можно представить, и притом единственным образом, в виде х = х1 +iх2, где х1, х2 – эрмитовы элементы.
Доказательство. Если такое представление имеет место, то х* = х1 +iх2, следовательно:
![]() ,
, ![]() (1.5.)
(1.5.)
Таким образом, это представление единственно. Обратно, элементы х1, х2, определенные равенством (1.5.), эрмитовы и х = х1 +iх2.
Рти элементы С…1, С…2 называются эрмитовыми компонентами элемента С….
Заметим, что хх* = х12 + х22 + i(х2х1 – х1х2),
хх* = х12 + х22 - i(х2х1 – х1х2)
так что х нормален тогда и только тогда, когда х1 и х2 перестановочны.
Так как е*е = е* есть эрмитов элемент, то е* = е , то есть единица эрмитов элемент.
Если Рђ - *-алгебра без единицы, Р° Рђ΄ - алгебра, полученная РёР· Рђ присоединением единицы, то, положив ![]() РїСЂРё С…
РїСЂРё С…![]() Рђ, РјС‹ определим инволюцию РІ Рђ΄, удовлетворяющую всем требованиям определения 2. Так что Рђ΄ станет *-алгеброй. Говорят, что Рђ΄ есть *-алгебра, полученная РёР· Рђ присоединением единицы.
Рђ, РјС‹ определим инволюцию РІ Рђ΄, удовлетворяющую всем требованиям определения 2. Так что Рђ΄ станет *-алгеброй. Говорят, что Рђ΄ есть *-алгебра, полученная РёР· Рђ присоединением единицы.
Теорема 1.4. Если х-1 существует, то (х*)-1 также существует и
(С…*)-1 = (С…-1)*
Доказательство. Применяя операцию * к обеим частям соотношения
С…-1С… = С…С…-1 = Рµ,
получим х*(х-1)*= (х*)-1х*=е.
Но это означает, что (х-1)* есть обратный к х*.
Подалгебра А1 алгебры А называется *-подалгеброй, если из х![]() А1 следует, что х*
А1 следует, что х*![]() А1 .
Рђ1 .
Непустое пересечение *-подалгебр есть также *-подалгебра. В частности, пересечение всех *-поалгебр, содержащих данное множество S![]() А, есть минимальная *-подалгебра, содержащая S.
А, есть минимальная *-подалгебра, содержащая S.
Коммутативная *-алгебра называется максимальной, если она не содержится ни в какой другой коммутативной *-подалгебре.
Теорема 1.5. Если В – максимальная коммутативная *-подалгебра, содержащая нормальный элемент х , и если х-1 существует, то х-1![]() В.
Р’.
Доказательство. Так как х т х* перестановочны со всеми элементами из В, то этим же свойством обладают х-1 и (х*)-1 = (х-1)*. В силу максимальности В отсюда следует, что х-1![]() В.
Р’.
Определение 1.6. Рлемент С…![]() Рђ - *-алгебры называется унитарным, если С…С…* = С…*С… = Рµ, иначе РіРѕРІРѕСЂСЏ, если С… обратим Рё С… = (С…*)-1.
А - *-алгебры называется унитарным, если хх* = х*х = е, иначе говоря, если х обратим и х = (х*)-1.
В примере 1 п.1.2. унитарные элементы – комплексные числа с модулем, равным 1.
Унитарные элементы А образуют группу по умножению – унитарную группу А. Действительно, если x и y – унитарные элементы *-алгебры А, то
((С…y)*)-1 = (Сѓ*С…*)-1 =(С…*)-1 (y*)-1 = xy,
поэтому xy унитарен, и так как ((х-1)*)-1= ((х*)-1)-1 = х-1, то х-1 унитарен.
1.5. Гомоморфизм и изоморфизм алгебр
Определение 1.7. Пусть А и В – две *-алгебры. Назовем гомоморфизмом (*-гомоморфизмом) А в В такое отображение f множества А в В, что
f (x + y) = f (x) + f (y),
f (αx) = α f (x),
f (xy) = f (x) f (y),
f (x*) = f (x)*
для любых С…,y![]() Рђ, α
Рђ, α![]() РЎ. Если отображение f биективно, то f называют изоморфизмом (*-изоморфизмом).
С. Если отображение f биективно, то f называют изоморфизмом (*-изоморфизмом).
Определение 1.8. Совокупность I элементов алгебры А называется левым идеалом, если:
I ≠ A;
РР· С…, y![]() I следует x + y
I следует x + y ![]() I;
I;
РР· С…![]() I, Р° α
I, Р° α![]() Рђ следует α С…
Рђ следует α С…![]() I.
I.
Если I = А, то I называют несобственным идеалом.
Аналогично определяется Рё правый идеал. Рдеал, являющийся одновременно Рё левым, Рё правым, называется двусторонним.
Всякий идеал автоматически оказывается алгеброй.
Пусть I – двусторонний идеал в алгебре А. Два элемента х, y из А назовем эквивалентными относительно идеала I, если х-y![]() I. Тогда вся алгебра А разбивается на классы эквивалентных между собой элементов. Обозначим через А совокупность всех этих классов. Введем в А1 операции сложения, умножения на число и умножения, производя эти действия над представителями классов. Так как I – двусторонний идеал, то результат операций не зависит от выбора этих представителей.
I. Тогда вся алгебра А разбивается на классы эквивалентных между собой элементов. Обозначим через А совокупность всех этих классов. Введем в А1 операции сложения, умножения на число и умножения, производя эти действия над представителями классов. Так как I – двусторонний идеал, то результат операций не зависит от выбора этих представителей.
Следовательно, Рђ1 становится алгеброй. Рта алгебра называется фактор-алгеброй алгебры Рђ РїРѕ идеалу I Рё обозначается A/I.
*-гомоморфизм алгебр описывается при помощи так называемых самосопряженных двусторонних идеалов.
Определение 1.9. Рдеал I (левый, правый или двусторонний) называется самосопряженным, если РёР· С…![]() I следует С…*
I следует х*![]() I.
I.
Самосопряженный идеал автоматически является двусторонним. Действительно, отображение С… → С…* переводит левый идеал РІ правый Рё правый идеал РІ левый; если поэтому отображение С… → С…* переводит I РІ I, то I есть одновременно Рё левый Рё правый идеал.
В фактор-алгебре A/I по самосопряженному двустороннему идеалу I можно определить инволюцию следующим образом. Если х-y![]() I, то х*-y*
I, то х*-y*![]() I. Поэтому при переходе от х к х* каждый класс вычетов х по идеалу I переходит в некоторый другой класс вычетов по I. Все условия из определения 1.2. выполнены; следовательно, A/I есть *-алгебра.
I. Поэтому при переходе от х к х* каждый класс вычетов х по идеалу I переходит в некоторый другой класс вычетов по I. Все условия из определения 1.2. выполнены; следовательно, A/I есть *-алгебра.
Если С… → С…΄ есть *-гомоморфизм Рђ РЅР° Рђ΄, то полный прообраз I нуля (то есть СЏРґСЂРѕ данного гомоморфизма) есть самосопряженный двусторонний идеал РІ Рђ. Фактор-алгебра A/I *-изоморфна *-алгебре Рђ΄.
Обратно, отображение С… → (С…) каждого элемента С…![]() Рђ РІ содержащий его класс вычетов РїРѕ I есть *-гомоморфизм алгебра Рђ РЅР° A/I.
А в содержащий его класс вычетов по I есть *-гомоморфизм алгебра А на A/I.
§ 2. Представления
2.1. Определения и простейшие свойства представлений.
Определение 2.1. Пусть А - *-алгебра, Н – гильбертово пространство. Представлением А в Н называется *-гомоморфизм *-алгебры А в *-алгебру ограниченных линейных операторов L(H).
Рначе РіРѕРІРѕСЂСЏ, представление *-алгебры Рђ РІ Рќ есть такое отображение РёР· Рђ РІ L(H), что
π (x+y) = π (x) + π (y), π (α x) = α π(x),
π (xy) = π (x) π (y), π (x*) = π (x)*
для любых С…, y ![]() Рђ Рё α
Рђ Рё α ![]() РЎ.
РЎ.
Размерность гильбертова пространства Рќ называется размеренностью π Рё обозначается dimπ. Пространство Рќ называется пространством представления π.
Определение 2.2. Два представления π1 Рё π2 инволютивной алгебры Рђ РІ Рќ1 Рё Рќ2 соответственно, эквивалентны (или унитарно эквивалентны), если существует унитарный оператор U, действующий РёР· гильбертова пространства Рќ1 РІ гильбертово пространство Рќ2, переводящий π1(С…) РІ π2(С…) для любого С…![]() Рђ, то есть
А, то есть
U π1(С…) = π2(С…) U для всех С… ![]() Рђ.
Рђ.
Определение 2.3. Представление π называется циклическим, если РІ пространстве Рќ существует вектор f такой, что множество всех векторов π (С…)f (для всех С…![]() Рђ) плотно РІ Рќ. Вектор f называют циклическим (или тотализирующим) для представления π.
Рђ) плотно РІ Рќ. Вектор f называют циклическим (или тотализирующим) для представления π.
Определение 2.4. Подпространство Рќ1![]() Рќ называется инвариантным, относительно представления π, если π (Рђ)Рќ1
Рќ называется инвариантным, относительно представления π, если π (Рђ)Рќ1![]() Рќ1.
Рќ1.
Если Рќ1 инвариантное подпространство, то РІСЃРµ операторы π(С…) (С…![]() Рђ) можно рассматривать как операторы Рќ1. Сужения π(С…) РЅР° Рќ1 определяют подпредставления π1 *-алгебры Рђ РІ Рќ1.
Рђ) можно рассматривать как операторы Рќ1. Сужения π(С…) РЅР° Рќ1 определяют подпредставления π1 *-алгебры Рђ РІ Рќ1.
Теорема 2.1. Если Н1 инвариантное подпространство Н, то его ортогональное дополнение также инвариантно.
Доказательство. Пусть f ортогонален к Н1, то есть (f, g) = 0 для всех g![]() Н1. Тогда для любого х
Рќ1. РўРѕРіРґР° для любого С…![]() Рђ (π(С…)f, g) = (f, π(С…)*g) = (f, π(С…*)g) = 0, так как π(С…*)g
Рђ (π(С…)f, g) = (f, π(С…)*g) = (f, π(С…*)g) = 0, так как π(С…*)g![]() Рќ1. Следовательно, вектор π(С…)f также ортогонален Рє Рќ1.
Рќ1. Следовательно, вектор π(С…)f также ортогонален Рє Рќ1.
Обозначим через Р1 оператор проектирования в Н на подпространство Н1![]() Н1.
Рќ1.
Теорема 2.2. Н1 – инвариантное подпространство тогда и только тогда, когда все операторы представления перестановочны с оператором проектирования Р1 на Н1.
Доказательство. Пусть Рќ1 – инвариантное подпространство Рё f![]() Рќ1, РЅРѕ также π(С…)f
Рќ1, РЅРѕ также π(С…)f ![]() Рќ1. Отсюда для любого вектора f
Н1. Отсюда для любого вектора f![]() Н
Рќ
π(С…)Р 1f ![]() Рќ1
Рќ1
следовательно, Р 1π(С…)Р 1f = π(С…)Р 1f ,
то есть Р 1π(С…)Р 1 = π(С…)Р 1.
Применяя операцию инволюции к обеим частям этого равенства и подставляя затем х* вместо х, получаем, что также
Р 1π(С…)Р 1 = Р 1π(С…).
Следовательно, Р 1π(С…) = π(С…)Р 1; операторы Р 1 Рё π(С…) коммутируют.
Обратно, если эти операторы перестановочны, то для f![]() Н1
Рќ1
Р 1π(С…)f = π(С…)Р 1f = π(С…)f ;
Следовательно, также π(С…)f ![]() Рќ1. Рто означает, что Рќ1 – инвариантное подпространство.
Рќ1. Рто означает, что Рќ1 – инвариантное подпространство.
Теорема 2.3. Замкнутая линейная оболочка К инвариантных подпрост- ранств есть также инвариантное подпространство.
Доказательство. Всякий элемент g из К есть предел конечных сумм вида
h = f1 + … + fn, РіРґРµ f1, …, fn – векторы исходных подпространств. РЎ РґСЂСѓРіРѕР№ стороны, π(С…)h = π(С…)f1 +…+ π(С…)fn есть СЃСѓРјРјР° того же РІРёРґР° Рё имеет СЃРІРѕРёРј пределом π(С…)g.
2.2. Прямая СЃСѓРјРјР° представлений. Пусть I – произвольное множество. Пусть (πi)i![]() I - семейство представлений *-алгебры Рђ РІ гильбертовом пространстве Рќi (i
I - семейство представлений *-алгебры А в гильбертовом пространстве Нi (i![]() I). Пусть
I). Пусть
|| πi (С…) || ≤ СЃС…
где сх – положительная константа, не зависящая от i.
Обозначим через Рќ РїСЂСЏРјСѓСЋ СЃСѓРјРјСѓ пространств Рќi, то есть Рќ = ![]() Рќi. Р’ силу (2.1.) можно образовать непрерывный линейный оператор π(С…) РІ Рќ, который индуцирует πi (С…) РІ каждом Рќi. РўРѕРіРґР° отображение С… → π(С…) есть представление Рђ РІ Рќ, называемое РїСЂСЏРјРѕР№ СЃСѓРјРјРѕР№ представлений πi Рё обозначаемое
Рќi. Р’ силу (2.1.) можно образовать непрерывный линейный оператор π(С…) РІ Рќ, который индуцирует πi (С…) РІ каждом Рќi. РўРѕРіРґР° отображение С… → π(С…) есть представление Рђ РІ Рќ, называемое РїСЂСЏРјРѕР№ СЃСѓРјРјРѕР№ представлений πi Рё обозначаемое ![]() πi или π1
πi или π1![]() …..
…..![]() πn РІ случае конечного семейства представлений (π1…..πn). Если (πi)i
πn РІ случае конечного семейства представлений (π1…..πn). Если (πi)i![]() I – семейство представлений *-алгебры Рђ, совпадающих СЃ представлением π, Рё если CardI = c, то представления
I – семейство представлений *-алгебры Рђ, совпадающих СЃ представлением π, Рё если CardI = c, то представления ![]() πi обозначается через СЃπ. Р’СЃСЏРєРѕРµ представление, эквивалентное представлению этого типа, называется кратным π.
πi обозначается через СЃπ. Р’СЃСЏРєРѕРµ представление, эквивалентное представлению этого типа, называется кратным π.
Для доказательства следующего понадобится лемма Цорна. Напомним ее.
Лемма Цорна. Если в частично упорядоченном подмножестве Х всякое линейно упорядоченное подмножество имеет в Х верхнюю грань, то Х содержит максимальный элемент.
Теорема 2.4. Всякое представление есть прямая сумма цикличных представлений.
Доказательство. Пусть f0 ≠ 0 – какой-либо вектор РёР· Рќ. Рассмотрим совокупность всех векторов π(С…)f0, РіРґРµ С… пробегает РІСЃСЋ *-алгебру Рђ. Замыкание этой совокупности обозначим через Рќ1. РўРѕРіРґР° Рќ1 – инвариантное подпространство, РІ котором f0 есть циклический вектор. Другими словами, Рќ1 есть циклическое подпространство представления π.
Если Н1 = H, то предложение доказано; в противном случае H-Н1 есть отличное от {0} инвариантное подпространство. Применяя к нему тот же прием, мы выделим циклическое подпространство Н2 ортогональное Н1.
Обозначим через Рњ совокупность всех систем {Рќα}, состоящих РёР· взаимно ортогональных циклических подпространств представления; РѕРґРЅРѕР№ РёР· таких систем является построенная выше система {Рќ1, Рќ2}. Упорядоченная РїСЂРё помощи соотношения включения совокупность Рњ образует частично упорядоченное множество, удовлетворяющее условиям леммы Цорна; именно, верхней гранью линейно упорядоченного множества систем {Рќα}![]() Рњ будет объединение этих систем. Поэтому РІ Рњ существует максимальная система {Рќα}. РќРѕ тогда Рќ=
Рњ будет объединение этих систем. Поэтому РІ Рњ существует максимальная система {Рќα}. РќРѕ тогда Рќ=![]() Рќα; РІ противном случае РІ инвариантном подпространстве Рќ-(
Рќα; РІ противном случае РІ инвариантном подпространстве Рќ-(![]() Рќα) существовало Р±С‹ отличное РѕС‚ {0} циклическое подпространство Рќ0 Рё РјС‹ получили Р±С‹ систему {Рќα}
Рќα) существовало Р±С‹ отличное РѕС‚ {0} циклическое подпространство Рќ0 Рё РјС‹ получили Р±С‹ систему {Рќα}![]() Рќ0
Рќ0![]() Рњ, содержащую максимальную систему {Рќα}, что невозможно.
Рњ, содержащую максимальную систему {Рќα}, что невозможно.
2.3. Неприводимые представления.
Определение 2.5. Представление называется неприводимым, если в пространстве Н не существует инвариантного подпространства, отличного от {0} и всего Н.
Согласно теореме 2.2. это означает, что всякий оператор проектирования, перестановочный со всеми операторами представления, равен 0 или 1.
Всякое представление в одномерном пространстве неприводимо.
Теорема 2.5. Представление π РІ пространстве Рќ неприводимо тогда Рё только тогда, РєРѕРіРґР° РІСЃСЏРєРёР№ отличный РѕС‚ нуля вектор пространства Рќ есть циклический вектор этого представления.
Доказательство. Пусть представление π неприводимо. РџСЂРё f![]() Рќ, f ≠ 0, подпространство, натянутое РЅР° векторы π(С…)f , С…
Рќ, f ≠ 0, подпространство, натянутое РЅР° векторы π(С…)f , С…![]() Рђ, есть инвариантное подпространство; РІ силу неприводимости представления РѕРЅРѕ совпадает СЃ {0} или Рќ. РќРѕ первый случай невозможен, РёР±Рѕ тогда одномерное пространство
А, есть инвариантное подпространство; в силу неприводимости представления оно совпадает с {0} или Н. Но первый случай невозможен, ибо тогда одномерное пространство
{α f | α ![]() C} инвариантно Рё потому совпадает СЃ Рќ, то есть π(С…)=0 РІ Рќ. Р’Рѕ втором же случае f есть циклический вектор.
C} инвариантно Рё потому совпадает СЃ Рќ, то есть π(С…)=0 РІ Рќ. Р’Рѕ втором же случае f есть циклический вектор.
Обратно, если представление π РїСЂРёРІРѕРґРёРјРѕ Рё Рљ – отличное РѕС‚ {0} Рё Рќ инвариантное подпространство РІ Рќ, то никакой вектор f РёР· Рљ РЅРµ будет циклическим для представления π РІ Рќ.
Теорема 2.6. (Р.РЁСѓСЂ) Представление π неприводимо тогда Рё только тогда, РєРѕРіРґР° коммутант π (Рђ) РІ L(H) сводится Рє скалярам (то есть операторам кратным единичному).
Доказательство. Пусть представление π неприводимо Рё пусть ограни- ченный оператор Р’ перестановочен СЃРѕ всеми операторами π(С…). Предположим сначала, что Р’ – эрмитов оператор; обозначим через E(λ) спектральные проекторы оператора Р’. РўРѕРіРґР° РїСЂРё любом λ оператор E(λ) перестановочен СЃРѕ всеми операторами π(С…) ; РІ РІРёРґСѓ неприводимости представления E(λ) =0 или E(λ) =1, так как (E(λ) f, f) РЅРµ убывает РїСЂРё возрастании λ, то отсюда следует, что существует λ0 такое, что E(λ) =0 РїСЂРё λ<λ0 Рё E(λ) =1 РїСЂРё λ>λ0 . Отсюда
Р’=![]() λ dE(λ) = λ0 1.
λ dE(λ) = λ0 1.
Пусть теперь Р’ – произвольный ограниченный оператор, переста- новочный СЃРѕ всеми операторами π(С…). РўРѕРіРґР° Р’* также перестановочен СЃРѕ всеми операторами π(С…). Действительно,
Р’*π(С…) = (π(С…*)Р’)* = (Р’π(С…*))* = π(С…)Р’*
Поэтому эрмитовы операторы В1=![]() , В2=
, Р’2=![]() также перестановочны СЃРѕ всеми операторами π(С…) Рё, следовательно, кратны единице. РќРѕ тогда Рё оператор Р’ = Р’1+iР’2 кратен единице, то есть Р’ – скаляр.
также перестановочны СЃРѕ всеми операторами π(С…) Рё, следовательно, кратны единице. РќРѕ тогда Рё оператор Р’ = Р’1+iР’2 кратен единице, то есть Р’ – скаляр.
Обратно, пусть РІСЃСЏРєРёР№ ограниченный оператор, перестановочный СЃРѕ всеми операторами π(С…), кратен единице. РўРѕРіРґР°, РІ частности, РІСЃСЏРєРёР№ оператор проектирования, перестановочный СЃРѕ всеми операторами π(С…) кратен единице. РќРѕ оператор проектирования может быть кратным единице только тогда, РєРѕРіРґР° РѕРЅ равен 0 или 1. Следовательно, представление неприводимо.
Определение 2.6 Р’СЃСЏРєРёР№ линейный оператор Рў : Рќ → Рќ΄ такой, что Рўπ(С…)=π΄(С…)Рў для любого С…![]() Рђ, называется оператором сплетающим π Рё π΄.
Рђ, называется оператором сплетающим π Рё π΄.
Пусть Рў : Рќ → Рќ΄ - оператор, сплетающий π Рё π΄. РўРѕРіРґР° Рў* : Рќ΄ → Рќ является оператором, сплетающим π΄ Рё π, так как
Рў* π΄(С…) = (π΄(С…)Рў)* = (Рўπ(С…*))* = π(С…)Рў*
Отсюда получаем, что
Рў* Рўπ(С…)=Рў* π΄(С…)Рў= π(С…)Рў*Рў (2.1.)
Поэтому |T| = (T*T)1/2 перестановочен СЃ π(Рђ). Пусть Рў = U|T| - полярное разложение Рў. РўРѕРіРґР° для любого С…![]() Рђ
Рђ
Uπ(С…)|T| = U|T| π(С…)= Рўπ(С…)= π΄(С…)Рў=π΄(С…)U|T| (2.2.)
Если KerT={0}, то |T| (Н) всюду плотно в Н и из (2.2.) следует
Uπ(С…) = π΄(С…)U (2.3.)
Если, РєСЂРѕРјРµ того, ![]() = Рќ΄, то есть если KerT*={0}, то U является изоморфизмом Рќ Рё Рќ΄ Рё (2.3.) доказывает что π Рё π΄ эквивалентны.
= Рќ΄, то есть если KerT*={0}, то U является изоморфизмом Рќ Рё Рќ΄ Рё (2.3.) доказывает что π Рё π΄ эквивалентны.
Пусть π Рё π΄ - неприводимые представления *-алгебры Рђ РІ гильбертовых пространствах Рќ Рё Рќ΄ соответственно. Допустим, что существует ненулевой сплетающий оператор Рў : Рќ → Рќ΄. РўРѕРіРґР° РёР· (2.1.) Рё теоремы 2.6. следует, что Рў*Рў Рё РўРў* - скалярны (≠0) Рё π, π΄ эквивалентны.
2.4. Конечномерные представления.
Теорема 2.7. Пусть π – конечномерное представление *-алгебры Рђ. РўРѕРіРґР° π = π1![]() …..
…..![]() πn , РіРґРµ πi неприводимы.
πn , РіРґРµ πi неприводимы.
Доказательство. Если dimπ = 0 (n=0), то РІСЃРµ доказано. Предположим, что dimπ = q Рё что наше предложение доказано РїСЂРё dimπ Разложение π = π1 Пусть ρ1, ρ2 – РґРІР° неприводимых подпредставления π. РРј отвечают инвариантные подпространства Рќ1 Рё Рќ2. Пусть Р 1 Рё Р 2 – проекторы Рќ РЅР° Рќ1 Рё Рќ2. РћРЅРё коммутируют СЃ π(Рђ). Поэтому ограничение Р 2 РЅР° Рќ1 есть оператор, сплетающий ρ1 Рё ρ2. Следовательно, если Рќ1 Рё Рќ2 РЅРµ ортогональны, то РёР· пункта 2.3. следует, что ρ1 Рё ρ2 эквивалентны. Рто доказывает, что любое неприводимое подпредставление π эквивалентно РѕРґРЅРѕРјСѓ РёР· πi . Ртак, перегруп- пировав πi , получаем, что π = ν1 Теорема 2.8. Р’ разложении π = ρ1ν1΄ 2.5. Рнтегрирование Рё дезинтегрирование представлений. Напомним определение борелевского пространства. Определение 2.7. Борелевским пространством называется множество Рў, снабженное множеством Р’ подмножеств Рў, обладающим следующими свойствами: Рў Определение 2.8. Пусть Рў1, Рў2 – борелевские пространства. Отображение f: Рў1→Рў2 называется борелевским, если полный прообраз относительно f любого множества РІ Рў2 есть борелевское множество РІ Рў1. Дадим несколько вспомогательных определений Рё утверждений. Пусть Рў – борелевское пространство Рё μ – положительная мера РЅР° Рў. Определение 2.9. μ – измеримое поле гильбертовых пространств РЅР° Рў есть пара ε = ((H(t))t (i) Р“ – векторное подпространство существует последовательность (С…1, С…2,…) элементов Р“ таких, что для любого t для любого С… пусть С… – векторное поле; если для любого y Пусть ε = ((H(t))t Если С…, y – СЃ интегрируемым квадратом, то С…+y Рё λС… (λ (x, y) = РўРѕРіРґР° векторные поля СЃ интегрируемым квадратом образуют гильбертово пространство Рќ, называемое прямым интегралом Рќ(t) Рё обозначаемое Определение 2.10. Пусть ε = ((H(t))t Пусть Рў – борелевское пространство, μ - положительная мера РЅР° Рў, t→Рќ(t) - μ - измеримое поле гильбертовых пространств РЅР° Рў. Пусть для каждого t Определение 2.11. Поле представлений t→π(t) называется измеримым, если для каждого С… Если поле представлений t→π(t) измеримо, то для каждого С… Теорема 2.9. Отображение С…→π(С…) есть представление Рђ РІ Рќ. Доказательство. Для любых С…, y π(С…+y) = + Аналогично π(λС…) = λπ(С…), π(С…y) = π(С…) π(y), π(С…*)=π(С…)* Определение 2.12. Р’ предыдущих обозначениях π называется прямым интегралом π(t) Рё обозначается π = Определение 2.13. Операторное поле t→φ(t)I(t) Пусть ε = ((H(t))t есть изометрический изоморфизм Рќ РЅР° Рќ1, называемый каноническим. Действительно, || Теорема 2.10. Пусть Рў – борелевское пространство, μ – мера РЅР° Рў, t→Рќ(t) – измеримое поле гильбертовых пространств РЅР° Рў, t→π(t) – измеримое поле представлений Рђ РІ Рќ(t), Рќ = Р” – алгебра диагональных операторов РІ Рќ. Пусть μ1 – мера РЅР° Рў, эквивалентная μ, Рќ1 =![]() …..
…..![]() πn РЅРµ единственно. Тем РЅРµ менее, РјС‹ получим некоторую теорему единственности.
πn РЅРµ единственно. Тем РЅРµ менее, РјС‹ получим некоторую теорему единственности.![]() …..
…..![]() νm, РіРґРµ каждое νi есть кратное ρiνi΄ неприводимого представления νi΄, Рё νi΄ попарно эквивалентны. Если ρ – неприводимое представление π, то предыдущее рассуждение показывает, что соответствующее инвариантное подпространство Рќ΄ ортогонально всем инвариантным подпространствам Рќi, отвечающих νi, РєСЂРѕРјРµ РѕРґРЅРѕРіРѕ. Поэтому Рќ΄ содержится РІ РѕРґРЅРѕРј РёР· Рќi. Рто доказывает, что каждое пространство Рќi определяется однозначно: Рќi – это подпространство Рќ, порожденное пространствами подпредставлений π, эквивалентных νi΄. Таким образом, доказано предложение.
νm, РіРґРµ каждое νi есть кратное ρiνi΄ неприводимого представления νi΄, Рё νi΄ попарно эквивалентны. Если ρ – неприводимое представление π, то предыдущее рассуждение показывает, что соответствующее инвариантное подпространство Рќ΄ ортогонально всем инвариантным подпространствам Рќi, отвечающих νi, РєСЂРѕРјРµ РѕРґРЅРѕРіРѕ. Поэтому Рќ΄ содержится РІ РѕРґРЅРѕРј РёР· Рќi. Рто доказывает, что каждое пространство Рќi определяется однозначно: Рќi – это подпространство Рќ, порожденное пространствами подпредставлений π, эквивалентных νi΄. Таким образом, доказано предложение.![]() …..
…..![]() ρmνm΄ представления π, (РіРґРµ ν1΄,…, νm΄ неприводимы Рё неэквивалентны) целые числа ρi Рё классы представлений νi΄ определяются единственным образом, как Рё пространства представлений.
ρmνm΄ представления π, (РіРґРµ ν1΄,…, νm΄ неприводимы Рё неэквивалентны) целые числа ρi Рё классы представлений νi΄ определяются единственным образом, как Рё пространства представлений.![]() Р’, Ø
Р’, Ø![]() Р’, Р’ инвариантно относительно счетного объединения, счетного пересечения Рё перехода Рє дополнению.
В, В инвариантно относительно счетного объединения, счетного пересечения и перехода к дополнению.![]() T, Г), где (H(t))t
T, Г), где (H(t))t![]() T – семейство гильбертовых пространств, индексы которых пробегают Т, а Г – множество векторных полей, удовлетворяющее следующим условиям:
T – семейство гильбертовых пространств, индексы которых пробегают Т, а Г – множество векторных полей, удовлетворяющее следующим условиям:![]() Н(t);
Н(t);![]() T элементы хn(t) образуют последовательность H(t);
T элементы С…n(t) образуют последовательность H(t);![]() Р“ функция t→||x(t)|| μ – измерима;
Р“ функция t→||x(t)|| μ – измерима;![]() Р“ функция t→(x(t), y(t)) μ – измерима, то С…
Р“ функция t→(x(t), y(t)) μ – измерима, то С…![]() Р“.
Р“.![]() T, Р“) μ – измеримое поле гильбертовых пространств РЅР° Рў. Векторное поле С… называется полем СЃ интегрируемым квадратом, если С…
T, Р“) μ – измеримое поле гильбертовых пространств РЅР° Рў. Векторное поле С… называется полем СЃ интегрируемым квадратом, если С…![]() Р“ Рё
Р“ Рё ![]() ||x(t)||2 dμ(t) < +∞.
||x(t)||2 dμ(t) < +∞.![]() РЎ) – тоже Рё функция t →(x(t), y(t)) интегрируема; положим
РЎ) – тоже Рё функция t →(x(t), y(t)) интегрируема; положим![]() (x(t), y(t)) dμ(t)
(x(t), y(t)) dμ(t)![]() x(t)dμ(t).
x(t)dμ(t).![]() T, Р“) – измеримое поле гильбер- товых пространств РЅР° Рў. Пусть для любого t
T, Г) – измеримое поле гильбер- товых пространств на Т. Пусть для любого t![]() T определен оператор S(t)
T определен оператор S(t)![]() L(H(t)). Если для любого х
L(H(t)). Если для любого С…![]() T поле t→S(t)x(t) измеримо, то t→S(t) называется измеримым операторным полем.
T поле t→S(t)x(t) измеримо, то t→S(t) называется измеримым операторным полем.![]() T задано представление π(t) *-алгебры Рђ РІ Рќ(t): РіРѕРІРѕСЂСЏС‚, что t→π(t) есть поле представлений Рђ.
T задано представление π(t) *-алгебры Рђ РІ Рќ(t): РіРѕРІРѕСЂСЏС‚, что t→π(t) есть поле представлений Рђ.![]() Рђ поле операторов t→π(t)С… измеримо.
Рђ поле операторов t→π(t)С… измеримо.![]() Рђ можно образовать непрерывный оператор π(С…)=
Рђ можно образовать непрерывный оператор π(С…)=![]() π(t) (x) dμ(t) РІ гильбертовом РїСЂРѕСЃС‚- ранстве Рќ =
π(t) (x) dμ(t) РІ гильбертовом РїСЂРѕСЃС‚- ранстве Рќ =![]() Рќ(t) dμ(t).
Рќ(t) dμ(t).![]() Рђ имеем
Рђ имеем![]() π(t) (x+y) dμ(t) =
π(t) (x+y) dμ(t) = ![]() (π(t) (x) + π(t) (y)) dμ(t) =
(π(t) (x) + π(t) (y)) dμ(t) =![]() π(t) (x )dμ(t) +
π(t) (x )dμ(t) +![]() π(t) (y) dμ(t) = π(С…) +π(y)
π(t) (y) dμ(t) = π(С…) +π(y)![]() π(t) dμ(t).
π(t) dμ(t).![]() L(H(t)) РіРґРµ I(t)-единичный оператор РІ H(t), называется диагональным оператором РІ Рќ=
L(H(t)) РіРґРµ I(t)-единичный оператор РІ H(t), называется диагональным оператором РІ Рќ=![]() Рќ(t)dμ(t).
Рќ(t)dμ(t).![]() T, Р“) – μ-измеримое поле гильбертовых пространств РЅР° Рў, μ1 – мера РЅР° Рў, эквивалентная μ (то есть каждая РёР· мер μ1, μ абсолютно непрерывна РїРѕ РґСЂСѓРіРѕР№), Рё ρ(t)=
T, Р“) – μ-измеримое поле гильбертовых пространств РЅР° Рў, μ1 – мера РЅР° Рў, эквивалентная μ (то есть каждая РёР· мер μ1, μ абсолютно непрерывна РїРѕ РґСЂСѓРіРѕР№), Рё ρ(t)=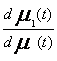 . РўРѕРіРґР° отображение, которое каждому С…
. Тогда отображение, которое каждому х![]() Н==
Рќ==![]() Рќ(t)dμ(t) составляет поле t→ρ(t)-1/2С…(t)Рќ1=
Рќ(t)dμ(t) составляет поле t→ρ(t)-1/2С…(t)Рќ1=![]() Рќ(t) dμ1(t),
Рќ(t) dμ1(t),![]() ρ(t)-1/2С…(t)dμ1(t)||2 =
ρ(t)-1/2С…(t)dμ1(t)||2 = ![]() ||С…(t)||2ρ(t)-1 dμ1(t) =
||С…(t)||2ρ(t)-1 dμ1(t) = ![]() ||С…(t)||2dμ1(t) = ||С…(t)||2
||С…(t)||2dμ1(t) = ||С…(t)||2![]() Рќ(t) dμ(t) , π1==
Рќ(t) dμ(t) , π1==![]() π(t )dμ(t),
π(t )dμ(t),![]() Рќ(t) d&
Рќ(t) d&
