Анализ рядов данных. Вычисление линии тренда для случаев однофакторной и многофакторной зависимостей.

Microsoft Excel: краткая информация о программе

Microsoft Excel (также иногда называется Microsoft Office Excel) -программа для работы с электронными таблицами, созданная корпорацией Microsoft. Она предоставляет возможности экономико-статистических расчетов, графические инструменты. Microsoft Excel входит в состав Microsoft Office и на сегодняшний день Excel является одним из наиболее популярных приложений в мире.

Области применения электронных таблиц:

· бухгалтерский и банковский учет;

· планирование распределение ресурсов;

· проектно-сметные работы;

· инженерно-технические расчеты;

· обработка больших массивов информации;

· исследование динамических процессов.

Основные возможности электронных таблиц:

· анализ и моделирование на основе выполнения вычислений и обработки данных;

· оформление таблиц, отчетов;

· форматирование содержащихся в таблице данных;

· построение диаграмм требуемого вида;

· создание и ведение баз данных с возможностью выбора записей по заданному критерию и сортировки по любому параметру;

· перенесение (вставка) в таблицу информации из документов, созданных в других приложениях, работающих в среде Windows;

· печать итогового документа целиком или частично.

Преимущества использования ЭТ при решении задач:

- Решение задач с помощью электронных таблиц освобождает от составления алгоритма и отладки программы. Нужно только определенным образом записать в таблицу исходные данные и математические соотношения, входящие в модель.

- При использовании однотипных формул нет необходимости вводить их многократно, можно скопировать формулу в нужную ячейку. При этом произойдет автоматический пересчет относительных адресов, встречающихся в формуле. Если же необходимо, чтобы при копировании формулы ссылка на какую-то ячейку не изменилась, то существует возможность задания абсолютного (неизменяемого) адреса ячейки.

 

Практическое занятие № 1

Анализ рядов данных. Вычисление линии тренда для случаев однофакторной и многофакторной зависимостей.

 

Постановка задачи: необходимо проанализировать представленные ряды данных и найти статистические зависимости между ними.

Исходные данные:

Месяц	Фрахтовая ставка, $/сут	Спрос, млн.т дедвейта	Предложение, млн. т дедвейта

 

А. Найти уравнение однофакторной зависимости изменения фрахтовой ставки во времени путем построения линии тренда.

1. Для анализа, из представленных данных возьмем столбцы «Месяц» и «Фрахтовая ставка». Построить график, представив данные в виде точечной диаграммы. При этом, по оси х располагается месяц, по оси у – фрахтовая ставка (рис.1).

 

2. Добавить на график линию тренда (рис. 2-4):

- правой кнопкой выделить точки графика и в появившемся меню выбрать «Добавить линию тренда» (тип линии тренда выбрать линейный);

- в том же меню, в последней закладке, выделить позиции «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации».

- появившуюся на графике линию тренда можно редактировать, вызвав правой кнопкой меню.

 

 

 

! Тип линии тренда подбирается, в зависимости от анализируемых данных, по показателю достоверности аппроксимации R². Чем ближе R² к единице, тем лучше линия тренда описывает данные.

3. Добавить в таблицу дополнительный столбец «Фрахтовая ставка теоретическая 1». Используя формулу линейного тренда, представленную на графике (y=70,536х+1855), рассчитать теоретические значения фрахтовой ставки.

 

Б. Найти уравнение многофакторной зависимости фрахтовой ставки от спроса и предложения на тоннаж путем выполнения регрессионного анализа.

1. В меню «Сервис» выбрать «Анализ данных». В появившемся меню выбрать инструмент анализа «Регрессия».

2. В открывшемся меню в активные строки входных интервалов ввести: входной интервал у – всю совокупность фактических значений фрахтовой ставки; входной интервал х – всю совокупность показателей, от которых ищется зависимость (а именно – спрос и предложение) (рис. 6).

 

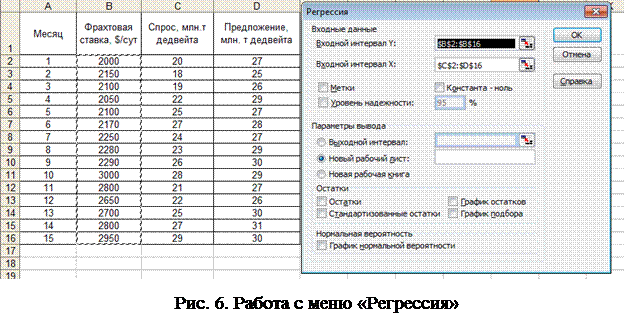3. Результат регрессионного анализа представлен на рис. 7. Для уравнения регрессии используются коэффициенты из нижней таблицы.

 

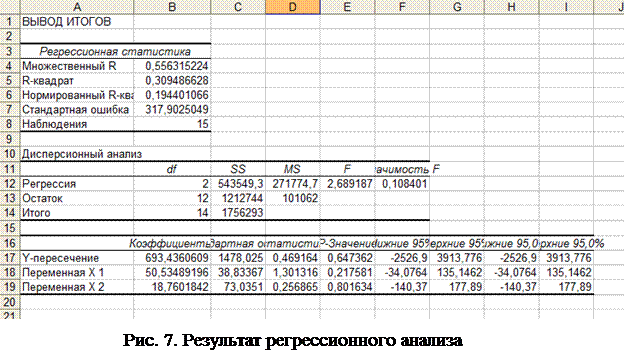
Уравнение регрессии для данного примера:

, (1)

где

Y-пересечение	693,43606=	b
Переменная X 1	50,53489=	a1
Переменная X 2	18,76018=	a2

 

Таким образом,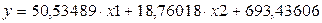

 

4. Формируем в таблице еще один столбец «Фрахтовая ставка теоретическая 2». В столбце, используя полученное уравнение регрессии, рассчитываем значения фрахтовой ставки.

 

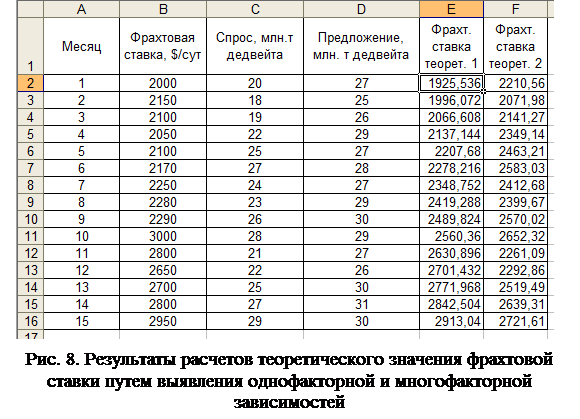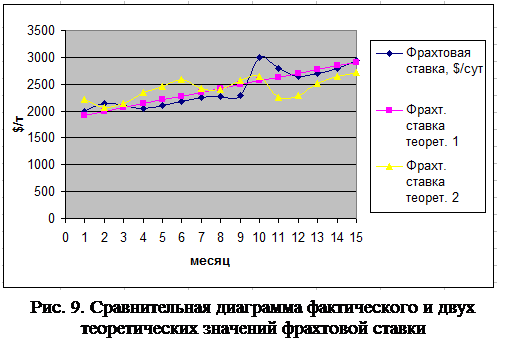
Результат расчетов изображаем графически (рис. 9).