ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
ИССЛЕДОВАНИЕ ДИНАМИКИ ПОСТУПАТЕЛЬНО-
Выполнил: Гладких Н.А.
Факультет : ЭА
Группа № 3401
Преподаватель: Морозов В.В
| Оценка лабораторно-практического занятия | ||||||||||
| Выполнение ИДЗ | Вопросы | Подготовка к лабораторной работе | Отчет по лабораторной работе | Коллоквиум | Комплексная оценка | |||||
“Выполнено” “____” ___________Подпись преподавателя __________
Лабораторная работа №6
ИССЛЕДОВАНИЕ ДИНАМИКИ
ПОСТУПАТЕЛЬНО-ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Цель работы: изучение законов поступательно-вращательного движения твердого тела, сохранения энергии, определение момента инерции маятника.
Приборы и принадлежности: маятник Максвелла, секундомер, масштабная линейка, штангенциркуль.
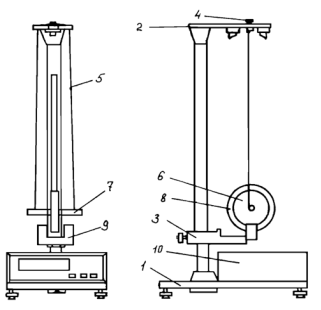 Маятник Максвелла (рис. 6.1) представляет собой диск 6, закрепленный на стержне 7, подвешенном на бифилярном подвесе 5 к верхнему кронштейну 2. На диск крепится кольцо 8. Верхний кронштейн 2, установленный на вертикальной стойке 1, имеет электромагнит и устройство 4 для регулировки длины бифилярного подвеса. Маятник с кольцом
Маятник Максвелла (рис. 6.1) представляет собой диск 6, закрепленный на стержне 7, подвешенном на бифилярном подвесе 5 к верхнему кронштейну 2. На диск крепится кольцо 8. Верхний кронштейн 2, установленный на вертикальной стойке 1, имеет электромагнит и устройство 4 для регулировки длины бифилярного подвеса. Маятник с кольцом
фиксируется в верхнем исходном положении с помощью электромагнита.
На вертикальной стойке 1 нанесена миллиметровая шкала, по которой определяется ход маятника. На нижнем кронштейне 3 находится фотоэлектрический датчик 9. Кронштейн обеспечивает возможность
перемещения фотодатчика вдоль вертикальной стойки и его фиксирования в любом положении в пределах шкалы 0…420 мм. Фотодатчик предназначен для выдачи электрических сигналов на секундомер 10 в момент пересечения светового луча оси фотодатчика диском маятника.
Результаты обработки эксперимента
| Таблица №1 | |||||||
| i | 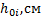
|  ,c ,c
| 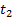 , c , c
| 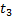 , c , c
| 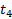 , c , c
|  , c , c
| tср, с |
| 3,944 | 4,046 | 3,891 | 3,977 | 3,933 | 3,958 | ||
| 3,505 | 3,595 | 3,531 | 3,541 | 3,547 | 3,544 | ||
| 3,374 | 3,195 | 3,324 | 3,202 | 3,194 | 3,258 | ||
| 2,832 | 2,772 | 2,835 | 2,790 | 2,824 | 2,810 |
Нахождение коэффициента «k» зависимости y=kx , где y=h, x=t2 и его погрешности ∆k.
Для оценки погрешности 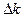 вычислим значение
вычислим значение  для всех значений
для всех значений 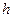 и
и  по формуле:
по формуле:
| Таблица №2 | ||
| h, м | t2, c | k |
| 0,36 | 15,7 | 0,0230 |
| 0,30 | 12,5 | 0,0240 |
| 0,25 | 10,6 | 0,0236 |
| 0,19 | 7,9 | 0,0240 |
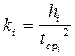 , i=1...5.
, i=1...5.
Пусть X=k, тогда
| Таблица №2 | |||||||
| № | max | min | xcр | ||||
| x | 0,0230 | 0,0240 | 0,0236 | 0,0240 | 0,0240 | 0,0236 | 0,02365 |
| (x-xср)2 | 0,00000042 | 0,00000012 | 0,000000025 | 0,00000012 |
| Таблица №3 | ||
| Формула | ||

| 0,02365 | 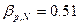
|
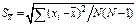
| 0,00018 | 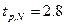
|
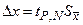
| 0,0005 | qh=0,00005 |
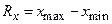
| 0,0004 | qt=0,0005 |
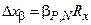
| 0,0002 | |
qx= 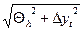
| 0,0005 | |
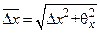
| 0,0007 |
| Таблица №4 | |
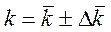
| 0,02365 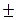 0,0007 0,0007
|
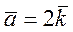
| 0,0473 |

| 0,0014 |
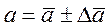
| 0,0473 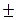 0,0014 0,0014
|
Вычисление 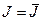
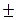
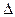
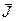 ( экспериментального значения момента инерции диска):
( экспериментального значения момента инерции диска):
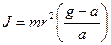 -> ln
-> ln 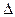
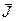 =ln m+2*ln r*ln(
=ln m+2*ln r*ln( 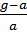 )
)
ba= 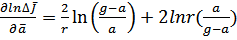 =2204,75
=2204,75
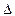
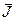 =
= 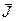
 =0,000043
=0,000043
| Таблица №5 | |
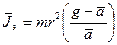
| 0,00094 |
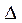 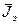
| 0,000043 |

| 0,00094 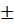 0,000043 0,000043
|
Вычисление 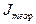 (теоретического значения момента инерции):
(теоретического значения момента инерции):
| Таблица №6 | |
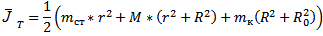
| 0,0007 |
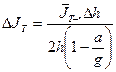
| 0,000013 |
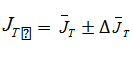
| 0,0007 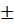 0,000013 0,000013
|
Нахождение теплоты:
 -0,052
-0,052
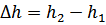 =0,028+0,052=0,08
=0,028+0,052=0,08
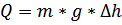 =0,341*10*0,08=0,3 Дж
=0,341*10*0,08=0,3 Дж
Вывод: Экспериментально значение момента инерции 0,00094 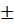 0,000043
0,000043
получилось больше теоретического 0,0007 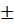 0,000013 вследствие того, что в расчётах не учитывалось сила трения. Но
0,000013 вследствие того, что в расчётах не учитывалось сила трения. Но  - величина, которая показывает на сколько завышена экспериментальные значения момента инерции и заодно доказывает верность расчётов.
- величина, которая показывает на сколько завышена экспериментальные значения момента инерции и заодно доказывает верность расчётов.