Построение номограммы тахеометра - автомата

Сначала проводят дугу окружности радиусом Rс центром в точке F (рис.7.10); пусть для конкретностиR =55 мм. Эта дуга является основной кривой, точка "нуль" которой наводится на нуль или нарис. 7.10.отсчетVрейки. Затем рассчитывают расстояния p_S иp_h для разных углов наклона при заданных значениях C=100, K=10 (K=20)иf_об= 251 мм; например:

ν = 0^o p_S = 2.51 мм ,

ν = 30^o p_S = 2.27 мми т.д.

Рис.7.10

Откладывают от радиусаFOуглы, для которых вычислены расстояния p_S и p_h; на стороне каждого угла откладывают эти расстояния от основной кривой и полученные точки соединяют плавными линиями - получаются линии номограммы. Для горизонтальных проложений строят две линии:C = 100 и C = 200, для превышений строят три линии:K = 10, K = 20 и K = 100для положительных и отрицательных углов наклона.

Номограмму строят либо на призме, либо на боковой поверхности либма вертикального круга; в поле зрения трубы изображение номограммы передается с помощью оптических деталей.

Из-за ошибок построения номограммы значения коэффициентов CиKмогут отличаться от проектных. Фактические значения коэффициентов определяют, измеряя многократно известное расстояниеS₀ и известное превышение h₀ :

C = S₀/l_S , K = h₀/l_h .

Относительная ошибка измерения расстояния номограммным тахеометром - 1/500, ошибка измерения превышений - 1 см на 100 м приK = 10и 2 см приK = 20.

Тахеометр-автомат часто применяют вместе со столиком Карти. В этом случае абрис составляют в процессе съемки на лавсановой пленке. Журнал съемки при этом не ведется, так как пикеты наносят на абрис в масштабе плана и сразу подписывают их отметки. При использовании столика Карти исключаются белые пятна - незаснятые участки местности в пределах станции.

В настоящее время для тахеометрической съемки применяются также электронные тахеометры, представляющие собой комбинацию точного теодолита и точного светодальномера.

 

Географическая система координат

Положение точки на любой поверхности или в пространстве определяется совокупностью конкретных величин, называемых координатами.Координаты могут выражаться как в линейной, так и в угловой мере; они определяют положение координатных линий относительно принятых за начало осей координат. Для определения положения точек на земной поверхности могут применяться различные системы координат: географическая, прямоугольная, полярная и др. Наиболее употребительной является система географических координат.
Малая ось эллипсоида пересекает поверхность последнего в двух точках, которые называются северными и южным полюсами. Плоскости, проходящие через ось вращения Земли, называются плоскостями земных меридианов, которые в сечении с поверхностью Земли образуют большие круги, называемые меридианами. Плоскость, перпендикулярная земной оси и проходящая через центр эллипсоида, называетсяплоскостью экватора. Большой круг, образующийся от пересечения этой плоскости с поверхностью эллипсоида, называется земным экватором. Плоскости, параллельные плоскости земного экватора в сечении с поверхностью Земли, образуют малые круги, называемыеземными параллелями.

Координатными осями системы географических координат приняты: экватор и один из меридианов, принимаемый за начальный; координатными линиями являются земные параллели и меридианы, а величинами, определяющими положение точек, т. е. координатами, географическая широта и географическая долгота.
Географической широтой точки на поверхности Земли называется угол между нормалью к поверхности эллипсоида в этой точке и плоскостью экватора. Географическая широта в кораблевождении обозначается греческой буквой φ (фи). Счет широт ведется от экватора к полюсам от 0 до 90°. Широты северного полушария считаются положительными и при аналитических расчетах они принимаются со знаком плюс. Северные широты обозначаются буквой N. Широты точек южного полушария, обозначаемые буквой S, считаются отрицательными и им приписывается знак минус.
Географическая широта определяет положение параллели, на которой находится определяемая точка.
Географической долготой точки называется двугранный угол, образованный плоскостью начального меридиана и плоскостью меридиана, проходящего через эту точку. Двугранный угол измеряется сферическим углом при полюсе между начальным меридианом и меридианом определяемой точки или численно равной ему дугой экватора, заключенной между названными меридианами.
За начальный меридиан в принципе может приниматься любой земной меридиан. По международному соглашению 1884 г. большинством стран мира, в том числе и Советским Союзом, за начальный принят меридиан, проходящий через Гринвичскую обсерваторию, расположенную около Лондона.
Счет географических долгот ведется к востоку и западу от Гринвичского меридиана от 0 до 180°. Географическая долгота в кораблевождении обозначается греческой буквой λ (ламбда). Долготы точек, находящихся в восточном полушарии, принято считать положительными (знак плюс), западные долготы считаются отрицательными (знак минус). При определении долготы той или иной точки земной поверхности обязательно указывают на ее наименование: восточной — Оst или, как сейчас принято, Е, западной — W. В зависимости от метода вычисления- географических координат различают координаты геодезические и астрономические.
В геометрическом определении геодезических координат, которые получаются в результате геодезических измерений (триангуляции, полигонометрии), никакой разницы с общей формулировкой географических координат нет. Места точек, фиксируемых геодезической широтой и геодезической долготой, относятся также к математически правильной фигуре—эллипсоиду вращения.
При определении места астрономическими способами наблюдатель имеет дело с линией отвеса, совпадающей с направлением силы тяжести, а не с нормалью к поверхности эллипсоида. Поэтому в астрономической системе координат широта определится как угол между плоскостью экватора и направлением отвеса в данной точке. Долгота места, определенного астрономическим способом, представляет собой двугранный угол между плоскостью начального меридиана (меридиана Гринвича) и плоскостью астрономического меридиана данной точки. Примененный термин—астрономический меридиан — надо понимать как след от сечения земной поверхности плоскостью, проходящей через отвесную линию в данной точке и параллельной оси мира. Из определения астрономических координат видно, что они в отличие от геодезических координат фиксируют положение точек относительно поверхности действительной фигуры Земли—геоида.

Нормаль к поверхности земного эллипсоида в общем случае не проходит через центр Земли. Вместе с тем при решении астрономических задач, а также ряда специальных задач математической картографии появляется необходимость определять положение точек земной поверхности относительно центра Земли. В этом случае долгота произвольной точки К определится также, как и в географической системе координат, а, широта получится как угол между плоскостью экватора и прямой, соединяющей данную точку с центром эллипсоида. Такая широта называется геоцентрической широтой и обозначается φ'. На рисунке видно, что геоцентрическая широта в общем случае меньше географической широты на величину редукции rшироты, которая может быть подсчитана по формуле
r'' = φ - φ' = α sin 2 φ / arc 1'' (3 формула)
Для точек, расположенных на экваторе и на полюсе, редукция широты равна нулю. Наибольшего значения (11,5') редукция достигает в широте 45°.
В случаях, когда форма Земли принимается за шар, положение точек на Земле—шаре определяется так же, как и на поверхности эллипсоида, их географическими координатами, т. е. широтой и долготой. Но нормаль на Земле—шаре совпадает с его радиусом.
Поэтому географической широтой φ некоторой точки М на земном шаре будет угол при центре сферы между плоскостью экватора и радиусом, проходящим через определяемую точку. Из сопоставления определений широты видно, что геоцентрическая широта является лишь частным случаем широты сферической.

Основные геометрические условия, которые должны быть соблюдены в теодолите, вытекают из принципиальной схемы измерения горизонтального угла и заключаются в следующем:

1) вертикальная ось инструмента должна быть отвесна;

2) плоскость лимба должна быть горизонтальна;

3) визирная плоскость должна быть вертикальна.

Проверка правильности работы инструмента и соблюдения его геометриче­ских условий называетсяповерками инструмента.

Для соблюдения этих условий выполняются следующие поверки теодо­лита:

1. Ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна к основной оси инструмента.

Устанавливают ось цилиндрического уровня параллельно двум подъемным винтам инструмента. Вращая винты в противоположные стороны, пузырек уровня устанавливают на середину (рис. 8.12, а). Поворачивают алидаду гори­зонтального круга на 180° (см. рис. 8.12, б). При отклонении пузырька уровня от се­редины более, чем на 1 деление, положение оси уровня исправляют исправи­тельными винтами уровня (см. рис. 8.9, винты 15; рис. 8.10, винты 11) на половину дуги отклонения.

I положение а) II положение б)

 

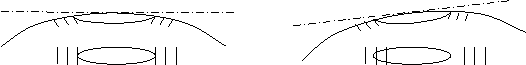
Рис. 8.12. К поверке уровня

2. Визирная ось трубы должна быть перпендикулярна к горизонтальной оси вращения трубы.

Угол отклонения визирной оси трубы от перпендикуляра к горизонтальной оси ее вращения называетсяколлимационной ошибкой трубы С.

Для проверки данного условия выбирают удаленную, находящуюся на го­ризонте ясно видимую точку М, визируют на нее при положении КЛ и делают отсчет по лимбу, например, КЛ = 125°12¢.

Затем переводят трубу через зенит, визируют на точку М при положении КП и снова берут отсчет по лимбу, например, КП = 305°16¢ (рис. 8.13, а).

Вычисляют двойную коллимационную ошибку по формуле

2С = КЛ - КП ± 180°, (8.1)

2С = 125°12¢ - 305°16¢ + 180° = -4¢ > ± 2¢ (допуск), а затем и С - коллимационную ошибку С = -2¢ > ± 1¢ (допуск).

Для исключения влияния коллимационной ошибки устанавливают на лимбе отсчет, вычисляемый по формулам

КЛиспр = КЛ - С (8.2)

или КПиспр = КП + С. (8.3)

КЛиспр = 125°12¢ - (-2¢) = 125°14¢,

КПиспр = 305°16¢ + (-2¢) = 305°14¢.

Центр сетки нитей при этом сойдет с точки М. Действуя боковыми испра­вительными винтами сетки, передвигают ее до совмещения центра сетки нитей с изображением точки М (см. рис. 8.13, б).

а) б)

 

Рис. 8.13. К поверке коллимационной ошибки

3. Горизонтальная ось вращения трубы должна быть перпендикулярна к вер­тикальной оси инструмента.

Установив теодолит в 30-40 м от стены какого-либо здания (рис. 8.14) и приведя лимб в горизонтальное положение, центр сетки нитей наводят на неко­торую высоко расположенную точку А стены. При закрепленной алидаде (при КЛ) наклоняют трубу до примерно горизонтального положения ее визирной оси и отмечают карандашом на стене точку а1 – проекцию центра сетки нитей. Переводят трубу через зенит, открепляют алидаду и при втором положении трубы (КП) снова наводят центр сетки нитей на точку А. Наклоняют трубу и отмечают карандашом на стене точку а2 – проекцию центра сетки нитей. При совпадении точек а1 и а2 условие выполняется. В противном случае (допуск - две проекции не должны выходить за пределы биссектора нитей сетки) ось вращения трубы неперпендикулярна к основной оси инструмента. Эта погреш­ность вызывается неравенством подставок, на которых располагается труба. В современных конструкциях инструментов подставки трубы не имеют исправи­тельных винтов, поэтому погрешность может быть устранена только в мастер­ской.

 

 

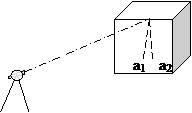
Рис. 8.14. К поверке равенства подставок

4. Одна из нитей сетки должна быть горизонтальна, другая вертикальна.

Наводят центр нитей сетки на какую-нибудь точку или отвес (рис. 8.15) и медленно поворачивают алидаду вертикального круга вокруг ее оси вращения, наблюдая за положением точки. Если при перемещении трубы изображение точки (отвеса) не будет сходить с вертикальной нити, то условие выполнено. В противном случае поворотом сетки нитей, при ее откреплении, производится исправление положения сетки.

 

 

Рис. 8.15. К поверке нитей сетки

5. Поверка места нуля вертикального круга.

Место нуля вертикального круга (МО) – отсчет по вертикальному кругу, когда визирная ось трубы горизонтальна, а пузырек уровня при алидаде нахо­дится на середине.

Зрительную трубу при КЛ наводят на некоторую точку М (рис. 8.16) и по­сле приведения пузырька уровня при алидаде горизонтального круга на сере­дину берут отсчет по вертикальному кругу, например, КЛ = 5°12¢. Аналогичные действия выполняют при КП, берут отсчет по вертикальному кругу, например, КП = 174°36¢.

Вычисляют место нуля по формуле

(8.4)

При значении места нуля более допуска, микрометренным винтом трубы (см. рис. 8.9, 13 или рис. 8.10,16) устанавливают на вертикальном круге отсчеты

КЛиспр = КЛ - МО (8.5)

или КПиспр = КП - МО. (8.6)

КЛиспр = 5°12¢ - (-6¢) = 5°18¢,

КПиспр = 174°36¢ - (-6¢) = 174°42¢.

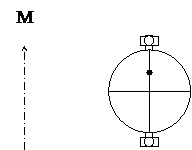Наблюдаемая точка М сместится по вертикали. Вертикальными исправительными винтами сетки перемещают изображение точки М до совмещения ее с центром сетки (рис. 8.16).

Геодезическая съемка. План, карта, профиль

Чтобы спроектировать линию местности на горизонтальную плоскость, нужно определить её горизонтальное проложение (проекцию линии на горизонтальную плоскость) и уменьшить его до определенного масштаба. Для проектирования на горизонтальную плоскость какого-либо многоугольника (рис. 26) измеряют расстояния между его вершинами и горизонтальные проекции его углов.

Совокупность линейных и угловых измерений на земной поверхности называется геодезической съемкой. По результатам геодезической съемки составляют план или карту.

Рис. 26. Проектирование участка земной поверхности на горизонтальную плоскость

План – чертеж, на котором в уменьшенном и подобном виде изображается горизонтальная проекция небольшого участка местности.

Карта – уменьшенное и искаженное, вследствие влияния кривизны Земли, изображение горизонтальной проекции значительной части или всей земной поверхности, построенное по определенным математическим законам.

Таким образом, и план, и карта – это уменьшенные изображения земной поверхности на плоскости. Различие между ними состоит в том, что при составлении карты проектирование производят с искажениями поверхности за счет влияния кривизны Земли, на плане изображение получают практически без искажений.

В зависимости от назначения планы и карты могут быть контурные и топографические. На контурных планах и картах условными знаками изображают ситуацию, т.е. только контуры (очертания) горизонтальных проекций местных предметов (дорог, строений, пашен, лугов, лесов и т.п.).

На топографических картах и планах кроме ситуации изображают ещё рельеф местности.

Для проектирования железных, шоссейных дорог, каналов, трасс, водопроводов и других сооружений необходимо иметь вертикальный разрез или профиль местности.

Профилем местности называется чертеж, на котором изображается в уменьшенном виде сечение вертикальной плоскостью поверхности Земли по заданному направлению.

Как правило, разрез местности (рис. 27, а) представляет собой кривую линию ABC...G. На профиле (рис. 27, б) она строится в виде ломаной линии abc...g. Уровенную поверхность изображают прямой линией. Для большей наглядности вертикальные отрезки (высоты, превышения) делают крупнее, чем горизонтальные (расстояния между точками).

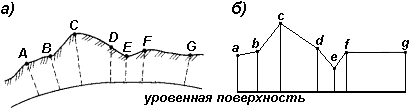
Рис. 27. Вертикальный разрез (а) и профиль (б) местности

Теодолиты – устройства, которые предназначены для измерения вертикальных и горизонтальных углов на месности. Теодолиты, в зависимости от точности, могут применяться в триангуляции, полигонометрии, в геодезических сетях сгущения. Также теодолиты нашли применение в прикладной геодезии, при проведении изыскательских работ. К тому же, теодолиты используют в промышленности при монтаже элементов конструкций машин, а также механизмов, строительстве промышленных сооружений и для выполнения иных задач.