Аналитический метод решения задач с параметрами.
Решить уравнение с параметрами означает следующее:
а) исследовать, при каких значениях параметров уравнение имеет корни и сколько их при различных значениях параметров;
б) найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.
 Пример.Решить уравнение:
Пример.Решить уравнение:
 .
.
Решение. Данное уравнение имеет один параметр  . Если
. Если 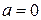 , то уравнение
, то уравнение 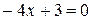 имеет один корень
имеет один корень  . При
. При 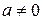 уравнение является квадратным и, исследуя дискриминант
уравнение является квадратным и, исследуя дискриминант  , получаем, что уравнение не имеет действительных корней, когда
, получаем, что уравнение не имеет действительных корней, когда  , т.е.
, т.е. 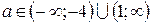 . При
. При  получаем, что для
получаем, что для  и
и  уравнение имеет одно решение, а при
уравнение имеет одно решение, а при  - два решения.
- два решения.
Поэтому ответ записывается так:
При 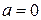
|  
|
При 
| 
|
При 
| 
|
При 
| 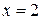
|
При 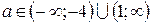
| Действительных корней нет. |
 Пример.При каких значениях параметра
Пример.При каких значениях параметра  уравнение:
уравнение:
 имеет ровно три корня.
имеет ровно три корня.
Решение. Перенесем все члены уравнения в левую часть и разложим на множители. Получим уравнение:
 или
или  .
.
Последнее уравнение равносильно совокупности двух уравнений:

Получим ровно три корня:
 и
и  ,
,
но при условии, что подкоренное выражение положительно:  . Решив это неравенство, получаем, что при
. Решив это неравенство, получаем, что при  уравнение имеет ровно три корня.
уравнение имеет ровно три корня.
 Пример.Для каждого значения параметра
Пример.Для каждого значения параметра  определить число решений уравнения:
определить число решений уравнения: 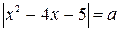 и найти их.
и найти их.
Решение. Заметим, что при  уравнение решения не имеет.
уравнение решения не имеет.
Если 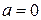 , то уравнение
, то уравнение 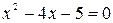 имеет два корня
имеет два корня  и
и  .
.
Рассмотрим случай 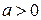 . Данное уравнение равносильно совокупности уравнений:
. Данное уравнение равносильно совокупности уравнений:

Решая их, получим 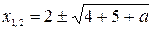 и
и  . Если дискриминанты
. Если дискриминанты  и
и  этих уравнений равны нулю, т.е. при
этих уравнений равны нулю, т.е. при  , каждое уравнение имеет по одному корню
, каждое уравнение имеет по одному корню 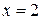 .
.
Если дискриминанты положительны:




Окончательно получим, что при  уравнение имеет четыре корня.
уравнение имеет четыре корня.