III. Алгебраические уравнения и системы уравнений
Пусть функции  и
и  определены на некотором множестве
определены на некотором множестве  . Поставим задачу: найти множество
. Поставим задачу: найти множество  , на котором эти функции принимают равные значения, другими словами, найти все значения
, на котором эти функции принимают равные значения, другими словами, найти все значения  , для которых выполняется равенство:
, для которых выполняется равенство:  =
=  .
.
При такой постановке это равенство называется уравнением с неизвестным  .
.
Уравнение называется алгебраическим, если в нем над неизвестным выполняются только алгебраические операции – сложение, вычитание, умножение, деление, возведение в степень и извлечение корня с натуральным показателем.
Множество  называется множеством (областью) допустимых значений неизвестного для данного уравнения.
называется множеством (областью) допустимых значений неизвестного для данного уравнения.
Множество  называется множеством решений, а всякое его решение
называется множеством решений, а всякое его решение  - корнем данного уравнения
- корнем данного уравнения
Решить уравнение, – значит, найти множество всех его решений или доказать, что их нет.
Уравнения, имеющие одни и те же корни, называются равносильными.
Основная теорема алгебры: всякое целое алгебраическое уравнение степени  в области комплексных чисел имеет
в области комплексных чисел имеет  корней.
корней.
Основные правила преобразования уравнения в равносильное ему:
· Какое-нибудь слагаемое можно перенести из одной части уравнения в другую с противоположным знаком;
· Обе части уравнения можно умножить или разделить на одно и тоже отличное от нуля число;
· Если уравнение имеет вид  , то деление обеих его частей на
, то деление обеих его частей на  , как правило, недопустимо, поскольку может привести к потере корней; в этом случае могут быть потеряны корни уравнения
, как правило, недопустимо, поскольку может привести к потере корней; в этом случае могут быть потеряны корни уравнения  =0, если они существуют;
=0, если они существуют;
· Уравнение вида  можно заменить равносильной системой
можно заменить равносильной системой  или решить уравнение
или решить уравнение  =0, а затем отбросить те из найденных корней, которые обращают в нуль знаменатель
=0, а затем отбросить те из найденных корней, которые обращают в нуль знаменатель  ;
;
· Уравнение считается решенным неверно как в случае, когда ответ содержит посторонние корни, так и в случае, когда в процессе решения был потерян хотя бы один корень.
Теорема о неэквивалентности уравнений: Если функции  и
и  имеют общую область определения, то уравнения
имеют общую область определения, то уравнения  =
=  и
и  2=
2=  2 не обязательно являются эквивалентными в этой области.
2 не обязательно являются эквивалентными в этой области.
Теорема об эквивалентности уравнений: Если функции  и
и  имеют общую область определения
имеют общую область определения  и для каждого значения переменной из области
и для каждого значения переменной из области  эти функции принимают неотрицательные значения, то уравнения
эти функции принимают неотрицательные значения, то уравнения  =
=  и
и  2=
2=  2 являются эквивалентными области
2 являются эквивалентными области  .
.
Некоторые типы уравнений и их корни
Линейное уравнение 
| |
 , ,  - любое число - любое число
| Уравнение имеет единственный корень, определяемый формулой 
|

| Уравнение имеет бесконечное множество корней, – любое число служит его корнем |
 , , 
| Уравнение корней не имеет, – ни одно число не может обратить его в справедливое равенство |
Квадратное уравнение 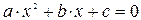 , дискриминант , дискриминант 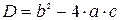
| ||

| 
| 
|

| 
| Среди действительных чисел корней нет |
Приведенное квадратное уравнение 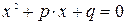 , дискриминант , дискриминант 
| ||

| 
| 
|

| 
| Среди действительных чисел корней нет |
Любой квадратный трехчлен можно представить в виде  , где
, где 
 , (выделен полный квадрат
, (выделен полный квадрат  ).
).
Для приведенного квадратного уравнения 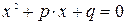 и при
и при  (т.е., если существуют корни), справедлива теорема Виета:
(т.е., если существуют корни), справедлива теорема Виета:

Квадратный трехчлен при условии  можно разложить на линейные множители
можно разложить на линейные множители  , где
, где  - корни. Если
- корни. Если  , то
, то  и его называют полным квадратом.
и его называют полным квадратом.
Биквадратным уравнением с одной неизвестной величиной  называется уравнение вида:
называется уравнение вида:  . Для ее решения от неизвестной величины
. Для ее решения от неизвестной величины  надо перейти к новой неизвестной величине
надо перейти к новой неизвестной величине  с помощью равенства:
с помощью равенства:  . Такого рода переход от одной неизвестной величины к другой называется методом замены неизвестных или подстановкой. Таким образом, исходное биквадратное уравнение сведется к квадратному уравнению относительно
. Такого рода переход от одной неизвестной величины к другой называется методом замены неизвестных или подстановкой. Таким образом, исходное биквадратное уравнение сведется к квадратному уравнению относительно  :
:  .
.
Иногда при решении уравнений высокой степени с целью упрощения полезно ввести новое неизвестное, и метод замены неизвестных наиболее эффективен.
 (1)
замена (1)
замена  получим: получим:
 (2) (2)
| ||||
| Корни уравнения (2) | 
| 
| ||
| Корни уравнения (1) | 
| 
| 
| 
|
| Ограничения | 
| 
| ||
В некоторых случаях может быть эффективным метод разложения левой части уравнения:  =0 на множители:
=0 на множители:

|

| 
|
Иррациональным называются уравнения, содержащие неизвестную величину под знаком радикала. Чтобы решить иррациональное уравнение, чаще всего приходится возводить его в степень, при этом нет никакой гарантии, что такого рода действия преобразуют данное уравнение в уравнение ему равносильное. Найдя корни этого уравнения, мы обязаны проверить, не являются ли они посторонними.
Два уравнения вида:

для которых ищется общее решение, образуют систему уравнений первой степени с двумя неизвестными.
Аналогично для любой системы алгебраических уравнений:

Две системы уравнений называют эквивалентными, если всякое решение одной системы является решением другой и, обратно, или если обе системы не имеют решений.
Существует три основных способа решения систем алгебраических уравнений: графический, метод подстановки и метод сложения.
 Пояснения к разделу: Алгебраические уравнения и системы уравнений.
Пояснения к разделу: Алгебраические уравнения и системы уравнений.
Процесс решения уравнения состоит в последовательной замене данного уравнения другим, более простым уравнением. Возникает вопрос о законности такой замены. Всегда ли получается уравнение с тем же множеством решений?
При решении уравнений необходимо следить за изменением множества допустимых значений неизвестного. В случае расширения его следует проверять, не является ли найденное решение посторонним для данного уравнения. В случае сужения необходимо убедиться, не являются ли выпавшие значения неизвестных решениями данного уравнения. Задача нахождения потерянных решений не всегда легко выполнима, поэтому желательно избегать тождественных преобразований, ведущих к сужению множества допустимых значений неизвестных уравнения.
Покажем, как решается биквадратное уравнение.
Пример. Решить уравнение:  .
.
Решение. От переменной  перейдем к новой неизвестной величине
перейдем к новой неизвестной величине  с помощью равенства:
с помощью равенства:  .
.
Таким образом, исходное биквадратное уравнение сведется к квадратному уравнению относительно  :
:  . Находим, что:
. Находим, что:
 ;
;
 ,
,
откуда находим, что:  и
и  .
.
Следовательно, имеем:

| 
| |

| 
| Корней нет |
Ответ:  ; ;  . .
| ||
Встречаются дробно-рациональные уравнения, которые сами не являются биквадратными, а только сводятся к ним. Таково, например, уравнение:
 .
.
Решение. Сложим дроби, расположенные в левой части уравнения:
 .
.
Приравняем к нулю числитель полученной дроби:
 .
.
Преобразовав и упростив левую часть, получим биквадратное уравнение:
 .
.
Решим ее обычным способом, найдем:
 ;
; 
 и
и  .
.
Следовательно, имеем:

| 
| ||

| 
| 
| 
|
Ни одно из этих чисел не обращает в нуль знаменатели дробей в исходном уравнении. Значит, эти числа и представляют собой искомые корни. Итак, данное уравнение имеет следующие четыре корня:
 ,
,  ,
,  ,
,  .
.
Рассмотрим несколько способов решения систем алгебраических уравнений. Пусть надо решить систему уравнений:

I способ (графический). Построим в одной координатной плоскости графики функций  и
и  (рис.3). Эти графики пересекаются в четырех точках. Абсциссы и ординаты точек пересечения являются корнями данной системы уравнений. Из рис.3 видно, что значения корней следующие:
(рис.3). Эти графики пересекаются в четырех точках. Абсциссы и ординаты точек пересечения являются корнями данной системы уравнений. Из рис.3 видно, что значения корней следующие:  .
.

| 
|
II способ (аналитический). Умножим второе уравнение на 2 и сначала сложим с первым, а затем вычтем из первого. Получим:
 или
или 
Задача сводится к системе линейных уравнений с двумя неизвестными:
 то есть
то есть 
Применяя к полученным системам метод сложения (т.е. сперва сложим эти уравнения, а далее вычтем из первых – вторые), получим:


 т.е. тот же ответ.
т.е. тот же ответ.
Рассмотрим еще один пример решения системы уравнений графическим и аналитическим способами.
Пусть надо решить систему уравнений:

I способ (графический). Построим в одной координатной плоскости графики функций  и
и  (рис.4). Эти графики также пересекаются в четырех точках
(рис.4). Эти графики также пересекаются в четырех точках  .
.
II способ (аналитический). Если применить метод подстановки, т.е. подставить в первое уравнение значение переменной  , выраженное через
, выраженное через  , после некоторых упрощений получим биквадратное уравнение:
, после некоторых упрощений получим биквадратное уравнение:
 ,
,
или в каноническом виде:  .
.
Корни последнего уравнения нетрудно найти:  .
.
Откуда, путем обратной подстановки в выражение  значений
значений  , находим:
, находим:  .
.
Итак, мы получили тот же ответ:  .
.
Остановимся теперь на основных способах решения простейших иррациональных алгебраических уравнений в области действительных чисел. Они основаны на возможности замены таких уравнений эквивалентными рациональными уравнениями «исключением радикалов».
| Методы решения иррациональных уравнений | |||||
| Уравнения, решаемые с помощью «арифметических» рассуждений | 
| 
| |||
| При каждом допустимом значении переменной сумма двух неотрицательных чисел не может быть отрицательна. | Решением уравнения является каждое значение  , для которого одновременно: , для которого одновременно:

| ||||
| Уравнение не имеет решений | Откуда  =1 =1
| ||||
| Уравнения, решаемые установлением множества допустимых значений | 
| 
| |||
ОДЗ переменной:    = =  . .
| ОДЗ переменной:    =3. =3.
| ||||
| Уравнение не имеет решений | Откуда устанавливаем проверкой, что  =3 =3
| ||||
| Способ уединения радикала | 
| ||||
ОДЗ переменной

| 
| ||||
| Уединение радикала | 
| ||||
| Возведение в квадрат | 
| ||||
| После упрощений | 
| ||||
| Еще раз возводим в квадрат | 
| ||||
| После упрощений | 
| ||||
| В итоге получим |  ОДЗ ОДЗ
|  ОДЗ ОДЗ
| |||
| Способ введения вспомогательных переменных | 
| ||||
| Вводим вспомогательные переменные | 
| ||||
Эквивалентная система уравнений, причем 
| 
| ||||
| Выразим из первого и вычтем второе из третьего | 

| ||||
| После подстановки | 
| ||||
| После упрощений |  или или

| ||||
| В итоге получим |  ОДЗ ОДЗ
| 
| |||