по выполнению лабораторной работы № 6

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Юго-Западный государственный университет»

 

Кафедра Телекоммуникаций

 

 

УТВЕРЖДАЮ   Первый проректор – проректор по учебной работе   ___________Е.А. Кудряшов   «_____»_____________2012 г.

 

 

Исследование частотного модулятора

Методические указания

по выполнению лабораторной работы № 6

по курсу «Теория электрической связи»

 

 

 

Курск 2012

УДК 621.391 (075)

 

Составители: С.Г. Лукьянюк

 

 

Рецензент

 

Кандидат технических наук, доцент С.Н. Михайлов

Исследование частотного модулятора [Текст]: методические указания по выполнению лабораторной работы № 6 по курсу «Теория электрической связи» / Юго-Западный. гос. ун-т; сост.: С.Г. Лукьянюк. Курск, 2012. 16 с.: ил. 3, табл. 4.

 

 

Содержит методические указания по выполнению лабораторной работы № 6 «Исследование частотного модулятора» по курсу «Теория электрической связи».

Методические указания соответствуют требованиям типовой программы, утверждённой УМО по специальности Телекоммуникации, и рабочей программы дисциплины «Теория электрической связи».

Предназначены для студентов специальностей 210400.68, 210402.65, 210404.65, 210406.65 дневной и заочной форм обучения.

 

Текст печатается в авторской редакции

 

 

Подписано печать . Формат 60х841/16.

Усл. печ. л. 0,82. Уч.-изд. л. Тираж экз. Бесплатно

Юго-Западный государственный университет.

305040, г. Курск, ул. 50 лет Октября, 94

Оглавление

 

1. Цель работы
2. Краткая характеристика исследуемых цепей и сигналов
3. Домашнее задание
4. Основы теории
5. Лабораторное задание
6. Методические указания
7. Отчёт
8. Контрольные вопросы

 

1 Цель работы

Исследование принципа действия частотного модулятора. Получение характеристик частотного модулятора при воздействии на его вход моногармонического сигнала. Исследование формы и спектра сигналов с частотной модуляцией.

 

2 Краткая характеристика исследуемых цепей и сигналов

В данной работе используется универсальный лабораторный стенд со сменным блоком ЧАСТОТНЫЙ МОДЕМ, упрощённая принципиальная схема которого приведена на рис. 1.

 

М О Д У Л Я Т О Р Д Е Т Е К Т О Р

мкА

С1

С2

С3

С4

С5

С6

С7

С8

С9

R1

R2

R3

R4

R5

R6

R7

EСМ

EС

КТ 1

КТ 2

КТ 4

VT1

VT2

VT3

A1

VD1

VD2

L1 L2

L3 L4

f01

f02

ФБЦ

КТ 3

 

Рисунок 1 – Схема блока ЧАСТОТНЫЙ МОДЕМ

 

Объектом исследования является левая часть схемы (между гнёздами КТ1 и КТ2). Исследуемый частотный модулятор представляет собой RC генератор, состоящий их двухкаскадного резистивного усилителя (А1) и фазобалансной цепи (ФБЦ), обеспечивающей положительную обратную связь. Частота генерации зависит от параметров ФБЦ – ёмкостей С3, С4 и сопротивлений каналов (R_СИ) полевых транзисторов VT1 и VT2. Сопротивление канала (R_СИ) зависит от управляющего напряжения, приложенного к затвору. Таким образом, полевой транзистор в ФБЦ является параметрическим элементом, управляемым модулирующим напряжением. Напряжение смещения (Е_см), являющееся постоянной составляющей модулирующего сигнала, позволяет установить несущую частоту модулированного сигнала, а переменная составляющая, т.е. сам модулирующий сигнал, поданный на гнезда КТ1, обеспечивает девиацию частоты Df_max, зависящую от амплитуды модулирующего сигнала. Выходом частотного модулятора являются гнезда КТ2.

В схеме модулятора имеется блок автоматической регулировки усиления, поддерживающий постоянную амплитуду ЧМ сигнала (на схеме не показан).

В качестве источника модулирующего сигнала используется встроенный диапазонный генератор, подключенный ко входу модулятора. Для контроля входного сигнала используется встроенный вольтметр или осциллограф. Анализ спектра производится на ПК в режиме «Спектроанализатор».

 

3 Домашнее задание

 

3.1 Изучите основные вопросы по конспекту лекций и литературе:

- Лукьянюк, С. Г. Теория электрической связи. Сигналы, помехи и системы передачи: учебное пособие. / С. Г. Лукьянюк, А. М. Потапенко / Юго-Зап. гос. ун-т. Курск, 2012. 235 с.;

- Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. Теория электрической связи. – М.: Радио и связь, 1998, с. 96 ¸102;

- Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2005, с.100¸108;

- Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Советское радио, 1977, с. 98¸107, 351¸359;

3.2 Оформите заготовку отчета. Выполните необходимые расчёты.

 

 

4 Основы теории

 

4.1 Угловая модуляция

 

Для описания модулированных колебаний удобно использовать квазигармоническую форму:

, (1)

где 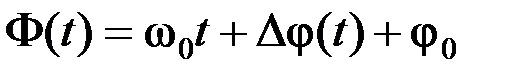– текущая фаза; 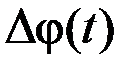– девиация (отклонение) фазы; 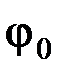– начальная фаза.

При угловой модуляции (УМ) огибающая U₀(t) не изменяется U₀(t) = const, а изменению подвергается либо фаза, либо её производная.

Фазовая модуляция (ФМ) – вид модуляции, при которой девиация фазы пропорциональна модулирующему сигналу u_с(t):

, (2)

где К_ФМ – константа, характеризующая работу модулятора.

Для частного случая – тональной ФМ, когда в качестве модулирующего сигнала используется гармонический сигнал низкой частоты (Ω << ω₀):

,

девиация фазы согласно (2) равна:

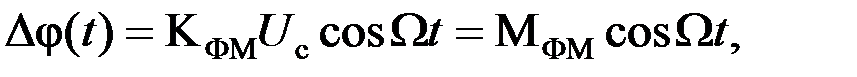(3)

где М_ФМ = К_ФМU_с= ∆φ_max – индекс фазовой модуляции, имеющий смысл максимальной девиации фазы. Подставив (3) в (1), получим выражение для тональной ФМ:

,

(в этом выражении и далее полагается ).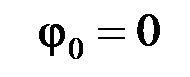

Частотная модуляция (ЧМ) – вид модуляции, при котором девиация частоты пропорциональна модулирующему сигналу:

где К_ЧМ – константа, характеризующая работу модулятора.

 

Производная от текущей фазы равна мгновенной частоте сигнала ω(t):

равной сумме несущей частоты ω₀ и девиации частоты ∆ω(t), изменяющейся под управлением модулирующего сигнала. В каждый момент времени мгновенная частота сигнала имеет только одно значение, в то время как спектр сигнала может состоять из большого числа частотных составляющих.

В частном случае тональной ЧМ:

, ,

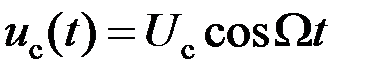мгновенная частота равна:

,

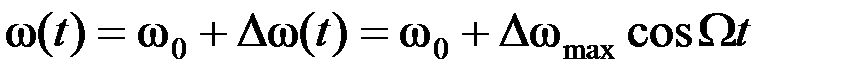а полная фаза:

Здесь М_ЧМ = ∆ω_max/Ω – индекс ЧМ, имеющий смысл максимальной девиации частоты. Подставив последнее выражение в (1), получим:

.

 

4.2 Спектры ФМ и ЧМ сигналов.

 

Из сопоставления выражений для тональных ФМ и ЧМ следует, что они отличаются только начальной фазой, что даёт основание рассматривать их как одно общее колебание с УМ:

.

Представим это выражение в комплексной форме (аналитический сигнал):

. (4)

Последний сомножитель в этом выражении является периодической функцией времени. Разложим его в ряд Фурье:

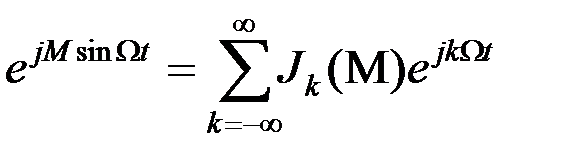. (5)

Коэффициентами разложения являются функции Бесселя первого рода k-го порядка от индекса модуляции М (рис. 2).

 

 

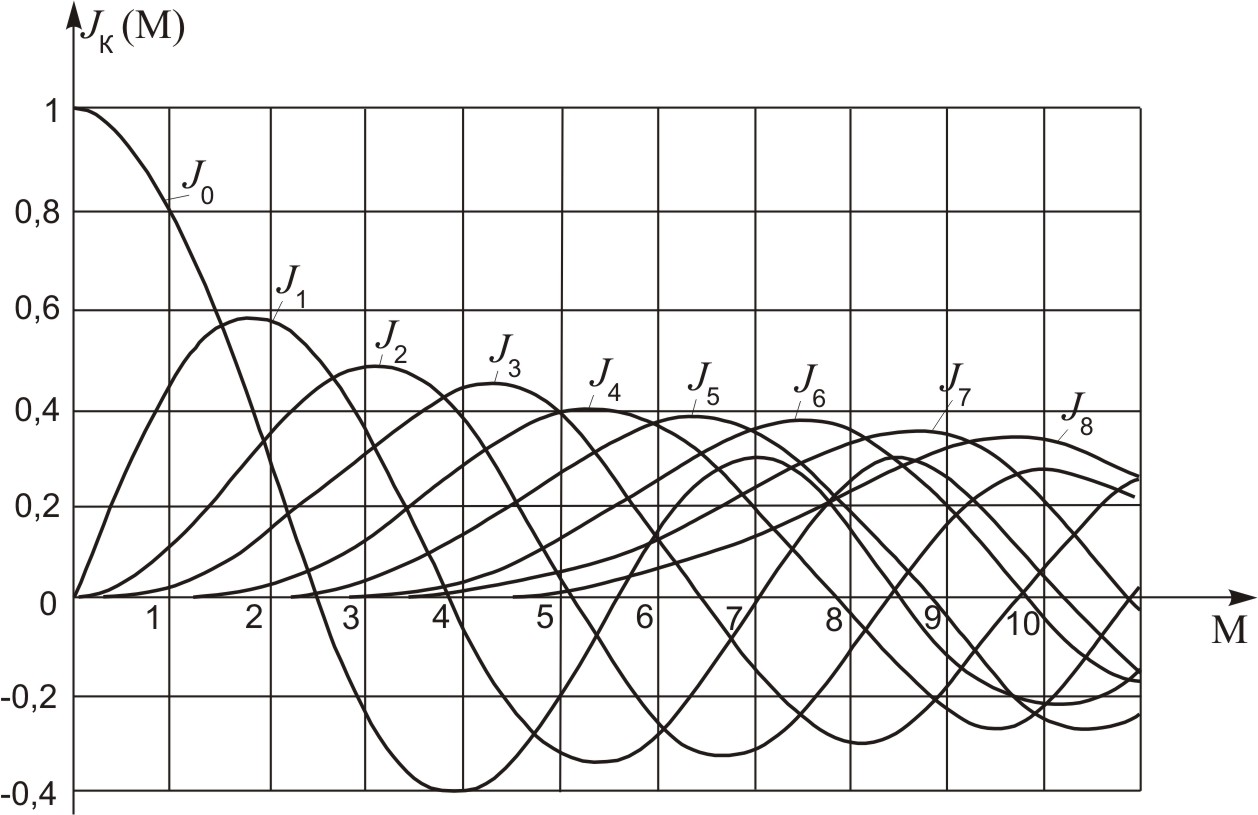
Рисунок 2 – Функция Бесселя для .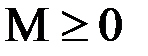

 

Подставив (6.5) в (6.4), получим:

.

Взяв вещественную часть от этого выражения, перейдем от комплексной записи к канонической форме квазигармонического колебания:

.

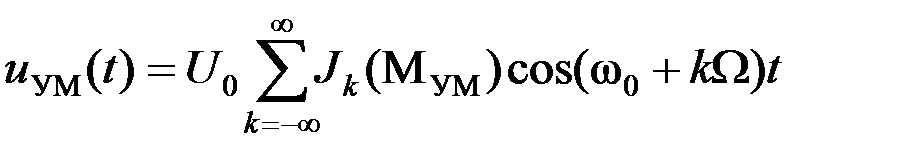Из этого выражения видно, что спектр амплитуд модулированного колебания состоит из бесконечного числа спектральных линий, расположенных на частотной оси с равномерным шагом W. Амплитуды спектральных линий определяются произведением амплитуды модулированного колебания U₀ на соответствующие значения функции Бесселя – U₀J_k(M). Но так как максимальное значение функции Бесселя равно единице (J₀при М= 0), то значения J_k(М) могут рассматриваться как относительные амплитуды спектральных составляющих.

Основные свойства функций Бесселя:

1) J_-k(M) = J_k(M) для четных k;

J_-k(M) = – J_k(M) для нечетных k.

Отсюда следует симметрия спектра амплитуд относительно несущей частоты (для которой k = 0);

2) J_k(-M) = J_к(M) для четных k;

J_k(-M) = –J_k(M) для нечетных k.

Следовательно, спектр амплитуд не зависит от того, увеличивается или уменьшается индекс модуляции. Знак минус здесь, как и в свойстве 1, не учитывается в спектре амплитуд, но проявляется только в спектре фаз;

3) J_k+1(k) > 0,1;

J_k+2(k) < 0,1;

4) .

Используя первую строчку свойства 3, запишем аналогичное неравенство для предыдущего значения k:

Практическая ширина спектра сигнала с УМ ограничивается составляющими с относительной амплитудой более 0,1 (относительная мощность больше 1%). Номер такой составляющей (k_гр) находится из последнего выражения при k = k_гр:

Аргументом функции Бесселя является индекс модуляции М, следовательно k_гр-1 = М, откуда:

k_гр = М + 1.

В соответствии со свойством 3, составляющая спектра с номером k_гр+1 имеет относительную амплитуду менее 0,1, т.е. окажется за пределами практической ширины спектра.

Последнее выражение позволяет по индексу модуляции М оценить число спектральных линий в практической ширине спектра. Так, например, при М= 3,2 граничное значение k_гр = 4 (ближайшее целое число). Следовательно, в спектре такого сигнала должны быть несущая и четыре пары боковых частот. Эти результаты легко проверить по графикам бесселевых функций (рис. 6.2). Действительно, четвертая пара боковых имеет относительную амплитуду J₄(3,2) = 0,16, т.е. находится в пределах практической ширины спектра, а следующая пятая пара боковых имеет относительную амплитуду J₅(3,2) = 0,04, т.е. находится за пределами этой полосы. Из рис. 3 следует, что практическая ширина спектра 2Δω* = 2W(М+1).

 

JK(M)

J0(M)

J-1(M)

J2(M)

JKгр(M)

J1(M)

J-2(M)

J-Kгр(M)

ω0+W

ω0

ω0+2W

ω0-W

ω0-2W

ω0-кгрW

ω0+кгрW

(1)

(0)

(2)

(-1)

(-2)

(-кгр)

(кгр)

ω

к

практическая ширина спектра

2Δω*=2Wкгр=2W(М+1)

0,1

 

Рисунок 3 – К определению практической ширины спектра при угловой модуляции

 

Здесь отложены относительные амплитуды J_k(M); для построения амплитудного спектра все составляющие следует умножить на U₀ = const.

Для ФМ М = М_ФМ. Индекс ФМ М_ФМ = Δφ_max и зависит от амплитуды модулирующего сигнала U_c. Поэтому практическая ширина спектра при ФМ равна:

2Δω*_ФМ = 2W(М_ФМ + 1)

и зависит как от частоты, так и от амплитуды модулирующего сигнала.

Для ЧМ М = М_ЧM = Δω_max/W, где Δω_max пропорциональна амплитуде модулирующего сигнала U_c:

.

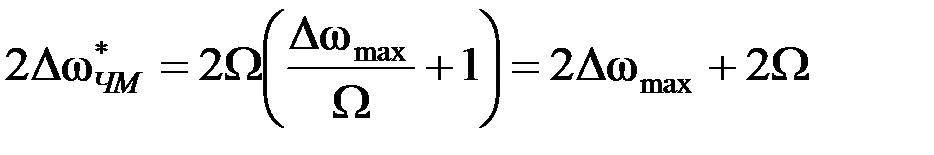Обычно Δω_max >> W и 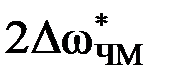, т.е. при ЧМ практическая ширина спектра зависит от амплитуды и почти не зависит от частоты модулирующего сигнала W. Следовательно, практическая ширина спектра ЧМ сигнала значительно меньше, чем для ФМ сигнала при тех же параметрах модуляции, что и определило широкое использование ЧМ в радиовещании и связи.

Выходная мощность передатчика с УМ на некоторой нагрузке R_H может быть найдена как сумма мощностей отдельных составляющих спектра:

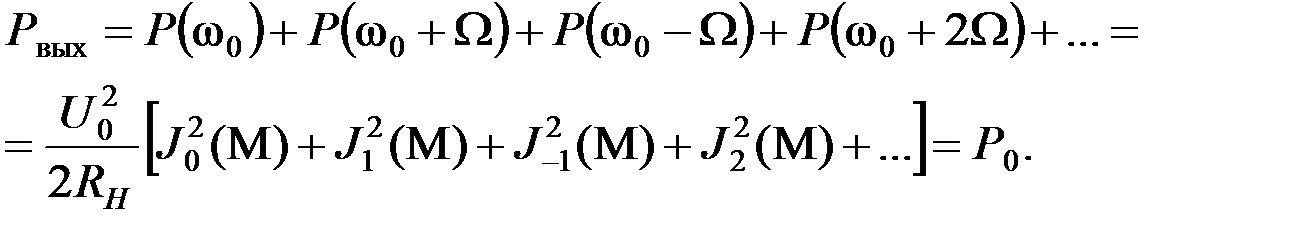
Здесь – мощность гармонического (немодулированного) сигнала, а сумма в квадратных скобках, согласно свойству 4 бесселевых функций, равна единице. Следовательно, мощность передатчика с угловой модуляцией остается постоянной независимо от параметров модуляции. В этом отношении ЧМ и ФМ выгодно отличаются от АМ, для которой выходная мощность передатчика меняется в больших пределах (например, при максимальной глубине модуляции М_АМ = 1, мощность передатчика АМ меняется от нуля до 4P₀).

 

5 Лабораторное задание

1) Проведите измерение статической модуляционной характеристики ЧМ модулятора и определите оптимальный его режим.

2) Определите влияние амплитуды модулирующего сигнала на форму и ширину спектра ЧМ-сигнала (при постоянной частоте модуляции).

3) Определите влияние частоты модуляции на форму и ширину спектра ЧМ-сигнала (при постоянной амплитуде модулирующего сигнала).

4) Проведите исследование формы сигнала на входе и выходе частотного модулятора.

6 Методические указания

6.1 Измерение статической модуляционной характеристики (СМХ) f = φ(Е_см) производится при отсутствующем модулирующем сигнале. Последовательно устанавливая движковым потенциометром Е_см значения напряжения смещения в соответствии с данными таблицы 1, определите значения частоты модулятора f, подключив выход модулятора (гнездо КТ2) ко входу ПК, работающего в режиме анализа спектра.

 

Таблица 1 – Экспериментальные значения СМХ ЧМ

Есм , B		-0,5	-1	-1,5	…………	-6,5
f , кГц

 

По данным таблицы постройте СМХ, по которой определите:

- положение рабочей точки (на середине линейного участка);

- величину Е_{см опт} и несущую частоту f₀ (по вертикальной оси);

- угол наклона линейного участка СМХ (тангенс этого угла соответствует коэффициенту К_ЧМмодулятора);

- границы линейного участка (f_min, f_max).

Полученные данные занесите в таблицу 2.

 

Таблица 2 – Результаты расчёта параметров ЧМ

Е см опт	f0	fmin	fmax	КЧМ

 

В случае хорошей линейности СМХ выбор несущей частоты некритичен, однако, для последующих пунктов лучше выбрать f₀= 12¸13 кГц.

6.2 Влияние амплитуды модулирующего сигнала на спектр ЧМ (при F_мод = const).

6.2.1 Для ряда заданных значений М_ЧМ (табл. 3) рассчитайте амплитуды модулирующих сигналов, а затем и действующие значения U_c.

Df_max находится из выражения для индекса ЧМ:

М_ЧМ = Δf_max/ F_мод. U_mc = D f_min / К_ЧМ.

Четвёртая строка таблицы заполняется для использования вольтметра переменного напряжения, имеющего градуировку в действующих значениях U_c = 0,707U_mc.

 

Таблица 3 – Влияние амплитуды модулирующего сигнала (F_мод= 500 Гц)

МЧМ		0,1	0,5	1,0	2,4	3,8
Dfmin
Umc
Uc
2Df *

 

6.2.2 Ко входу модулятора (гнездо КТ 1) подключите внутренний звуковой генератор и вольтметр переменного напряжения стенда или осциллограф. Установите частоту генератора F_мод = 500 Гц.

6.2.3 Устанавливая регулятором напряжения выхода генератора последовательно значения U_c в соответствии с табл. 3, с помощью ПК, подключённого к выходу модулятора (гнездо КТ 2) измерьте спектры ЧМ – сигнала.

На каждой спектрограмме укажите:

- условия проведения эксперимента;

- частоты отдельных составляющих спектра;

- практическую ширину спектра 2Df * (при определении 2Df * учьтите только ту часть спектра, в которой амплитуды более 10% от максимальных амплитуд).

Полученные значения 2Df * внесите в табл. 3.

6.3 Влияние частоты модуляции на спектр ЧМ-сигнала (U_C = const).

6.3.1 Сохраняя схему соединений (п. 6.2), установите значения U_C в соответствии с табл. 3 для М_ЧМ = 2,4 и не изменяйте его в дальнейшем.

6.3.2 Последовательно устанавливая частоты модуляции в соответствии с табл. 4, получите спектрограммы соответствующих ЧМ-сигналов. В таблицу внесите значения 2Df *.

 

Таблица 4 – Влияние частоты модуляции (U_C = const)

UC = …… B; f0 = …… кГц
Fмод, Гц
2Df *, Гц
МЧМ

 

6.3.3 Заполните последнюю строку табл. 4, используя определение М_ЧМ и необходимые данные из табл. 3.

6.4 Исследование формы колебаний на входе и выходе ЧМ.

6.4.1 Соедините первый вход двухлучевого осциллографа со входом модулятора (для чего отключите вольтметр, сохраняя соединение с генератором). На второй вход осциллографа подайте выходной сигнал модулятора.

6.4.2 Установите частоту модуляции F_мод = 300 Гц. Увеличивая уровень сигнала, добейтесь появления на осциллограмме выходного сигнала паразитной амплитудной модуляции. Уменьшая уровень входного сигнала, добейтесь постоянства уровня ЧМ – сигнала.

6.4.3 Установите синхронизацию осциллографа по каналу, на вход которого подан высокочастотный (выходной) сигнал. Ручками синхронизации добейтесь неподвижного изображения.

6.4.4 Подстраивая в небольших пределах частоту модуляции, добейтесь неподвижного изображения модулирующего сигнала. Иногда нужный эффект может быть достигнут небольшой подстройкой несущей частоты (ручкой СМЕЩЕНИЕ).

6.4.5 Зафиксируйте осциллограммы на входе и выходе ЧМ.

 

7 Отчет

Отчёт по форме и содержанию должен соответствовать требованиям, изложенным в разделе 3 (Оформление отчётов) Общих положений.

Отчёт должен содержать:

1) структурную схему лабораторной установки для выполнения исследований;

2) статическую модуляционную характеристику;

3) спектры, таблицы и осциллограммы по всем пунктам исследований;

4) теоретический расчёт спектров:

- п. 6.2.1, для М_ЧМ = 2,4 (из табл. 3);

- п. 6.3.1, для F_мод= 250 Гц (из табл. 4).

Для расчётов принять U₀= 1 В (амплитуда немодулированного сигнала);

5) обобщение результатов и выводы.

8 Контрольные вопросы

1) Дайте определение ЧМ - сигнала.

2) Приведите пример записи тонального ЧМ - сигнала с параметрами: f₀ = 100 МГц; F_мод= 10 КГц; Df_max = 50 кГц.

3) Объясните принцип действия частотного модулятора. Какие Вам известны способы получения ЧМ - сигналов?

4) Дайте определение статической модуляционной характеристики и объясните её смысл.

5) Что такое угловая модуляция?

6) Как рассчитать спектр ЧМ - сигнала?

7) Представьте (качественно) спектр колебания:

u (t) = U ₀cos(ω₀ t + 0,01cos Ω t).

8) Какое отношение имеют функции Бесселя к частотной модуляции?

9) Сколько спектральных линий надо учесть в практической ширине спектра ЧМ при М_ЧМ = 4?

10) Назовите известные Вам области применения ЧМ сигналов.