Лабораторная работа № 5
Построение различных типов диаграмм. Решение задач линейной оптимизации, применение сценариев.
Цель занятия: Закрепить умения по построению различных типов диаграмм, редактированию и изменению их типов. Решение задач линейной оптимизации, нахождению нескольких неизвестных параметров. Закрепить умения по составлению сценариев для осуществления прогноза.
Основная литература:
Уокенбах, Джон. Microsoft Excel 2010. Библия пользователя.: Пер.с англ. – М.: ООО «И.Д.Вильямс», 2011.-312 с. : ил. – Парал.тит.англ.
Дополнительная литература:
Волков В.Б. Понятный самоучитель Excel 2010. – СПб.:Питер, 2010.-256с.:ил.
Кулешова О.В., Центр Компьютерного обучения «Специалист», Microsoft Excel 2010. Анализ и визуализация данных. Решения практических задач. Методическое пособие, 2012.
Ход работы
Задание 1. Построить график функции.
1.Построение трехлепестковой розы.
Построить функцию, заданную уравнением: 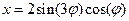 ,
,  .
.
Для построения графика функции используется тип диаграммы Точечная. Выделяется только диапазон значений x и y.
Построим таблицу и произведем расчеты: 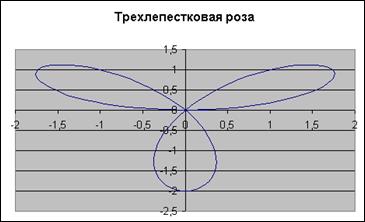

Для получения полной трехлепестковой розы значение fi должно быть от 0 до 3,2.
Формулы для вычисления:
| Ячейка | Формула |
| В2 | =2*SIN(3*A2)*COS(A2) |
| С2 | =2*SIN(3*A2)*SIN(A2) |
2.Построить график функции: 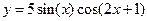
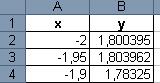
3.Построить график функции (Декартов лист): 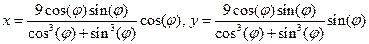 . Fi из диапазона -0,15 до 2 шагом 0,05.
. Fi из диапазона -0,15 до 2 шагом 0,05.
4.Построить Верьсьеру: 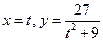 . Принять t от -5 до 5 шагом 0,3.
. Принять t от -5 до 5 шагом 0,3.
5.Построить Лемнискату Бернулли: 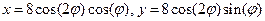 . Fi возьмите из диапазона от -3 до 0 с шагом 0,1.
. Fi возьмите из диапазона от -3 до 0 с шагом 0,1.
6.Построить Улитку Паскаля: 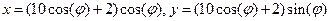 . Fi от -2 до 4,3 с шагом 0,1.
. Fi от -2 до 4,3 с шагом 0,1.
7.Построить Астроиду: 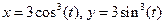 . Примите t от -3 до 3 с шагом 0,1.
. Примите t от -3 до 3 с шагом 0,1.
8.Построить поверхность: 
Задание 2. Фирма выпускает два типа строительных материалов: А и В. Продукция обоих 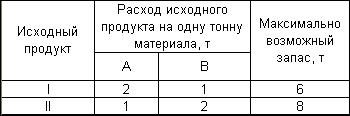 видов поступает в продажу. Для производства материалов используются два исходных продукта I и II. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице
видов поступает в продажу. Для производства материалов используются два исходных продукта I и II. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице
Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 т. Кроме того, установлено, что спрос на материал А никогда не превышает 2 т в сутки. Оптовые цены одной тонны материалов равны: 3000 у.е. для В и 2000 у.е. для А. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным?