Произвольная плоская система сил (задача С1)
5.1.1 Порядок решения задач при определении опорных реакций
твердого тела
Задачи на равновесие твердого тела при действии на тело плоской системы сил рекомендуется решать в следующем порядке:
1) выделить твердое тело, равновесие которого надо рассмотреть для определения искомых величин;
2) приложить заданные силы к рассматриваемому телу;
3) применив принцип освобождаемости от связей, изобразить силы реакций связей; чтобы задача являлась статически определимой, количество неизвестных опорных реакций должно соответствовать числу возможных уравнений равновесия;
4) выбрать систему осей декартовых координат;
5) составить уравнения равновесия плоской системы сил;
6) решив систему уравнений равновесия, определить неизвестные величины;
7) произвести проверку правильности решения задачи.
5.1.2 Условие задачи
Жесткая рама (рисунки 2, 3, 4, 5) закреплена в точках А и В с помощью неподвижного шарнира либо шарнирной опоры на катках или присоединена к невесомому стержню с шарнирами на концах. На раму действует пара сил с моментом М, распределенная нагрузка интенсивностью 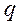 и две силы
и две силы  и
и  , направления и точки приложения которых указаны на рисунках. Исходные данные к расчету приведены в таблице 2.
, направления и точки приложения которых указаны на рисунках. Исходные данные к расчету приведены в таблице 2.
Необходимо определить реакции связей в точках А и В, вызываемые действующими нагрузками и выполнить проверку правильности решения задачи.
Указания.При решении задачи необходимо учесть, что уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы  часто удобно разложить ее на составляющие
часто удобно разложить ее на составляющие  и
и 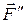 , плечи которых легко определяются, и воспользоваться теоремой Вариньона; тогда
, плечи которых легко определяются, и воспользоваться теоремой Вариньона; тогда  (
(  ) =
) =  (
( 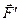 ) +
) +  (
( 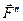 ).
).
5.1.3 Пример решения задачи С1
Жесткая пластина АВСD (рисунок 1) имеет в точке А неподвижную шарнирную опору, а в точке В – подвижную шарнирную опору на катках.
Все действующие нагрузки и размеры показаны на рисунке.
Д а н о: F1 = 25 кН,  =
=  , F2 = 18 кН,
, F2 = 18 кН, 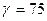 о, М = 50 кНм,
о, М = 50 кНм,  ,
,
q = 20 кН/м, а = 0,5 м.
Определить реакции в точках А и В, вызываемые действующими нагрузками и выполнить проверку правильности решения задачи.
 Рисунок 1
Рисунок 1
Решение задачи
1.Рассмотрим равновесие пластины. Проведем координатные оси X и Y и изобразим приложенные к пластине силы. Связи, наложенные на пластину, заменяем их реакциями  ,
,  ,
,  (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, направленными вдоль координатных осей, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
(реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, направленными вдоль координатных осей, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
2.Распределенную нагрузку интенсивностью  заменяем сосредоточенной силой
заменяем сосредоточенной силой  , модуль которой равен площади эпюры распределения, а точка приложения расположена в ее центре тяжести. В данном случае получим
, модуль которой равен площади эпюры распределения, а точка приложения расположена в ее центре тяжести. В данном случае получим  =
= 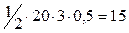 кН.
кН.
3.Для полученной плоской системы сил составим три уравнения равновесия, при этом для вычислении момента силы  относительно точки А воспользуемся теоремой Вариньона (см. выше). Получим:
относительно точки А воспользуемся теоремой Вариньона (см. выше). Получим:
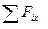 = 0,
= 0,  +
+  sin
sin 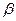 - F1 cos
- F1 cos  + F2 sin
+ F2 sin 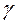 = 0; (1)
= 0; (1)
 = 0,
= 0, 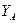 +
+  cos
cos 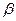 + F1 sin
+ F1 sin  – F2 cos
– F2 cos 
 = 0; (2)
= 0; (2)

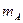 (
(  ) = 0, M –
) = 0, M –  cos
cos 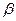 4а+ F1 cos
4а+ F1 cos  2а – F1 sin
2а – F1 sin  3а –
3а –
– F2 sin  2а
2а  = 0. (3)
= 0. (3)
Решив уравнения (1),(2),(3) с учетом численных значений заданных величин, определим искомые реакции.
О т в е т: XA= - 10,70 кН; YA= - 12,06 кН; RB= 11,63 кН.
Знаки минус указывают, что реакции 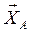 и
и 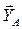 направлены противоположно показанным на рисунке 1.
направлены противоположно показанным на рисунке 1.
Для проверки правильности решения задачи необходимо составить уравнение суммы моментов сил, приложенных к пластине (с учетом реакций связей). В качестве моментной рекомендуется выбрать точку, не совпадающую с опорными. В данном случае составим уравнение моментов относительно точки E – точки приложения силы  :
:
 (4)
(4)
С учетом численных значений исходных данных и найденных значений реакций связей получим 0,01 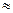 0.
0.
Следовательно, задача решена правильно.
Таблица 2
| Номер варианта | F1,Н | F2,Н |  ,
град. ,
град.
| 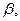 град.
град.
| М, Нм | q,  Н/м
Н/м
|



 5.2 Простейшие движения твердого тела
5.2 Простейшие движения твердого тела
5.2.1 Условие задачи
Механизм (рисунки 7, 8, 9, 10, 11) состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении или связанных между собой ременной передачей, с зубчатой рейкой 4, груз 5 находится на конце нити, намотанной на один из шкивов.
Для момента времени t = 1с определить и изобразить на рисунке (без масштаба) скорости и ускорения точек А, В, С механизма, а также скорости и ускорения рейки 4 и груза 5. Исходные данные к расчету приведены в таблице 3.
5.2.2 Пример решения задачи К1
Механизм состоит из ступенчатых колес 1 и 2, связанных между собой ременной передачей, колеса 2 и 3 находятся в зацеплении, колесо 1 находится в зацеплении с зубчатой рейкой 4, груз 5 находится на конце нити, намотанной на шкив 3 радиуса  (рисунок 6).
(рисунок 6).
Определить скорости точек В и С, ускорение груза 5, ускорение точки А и угловое ускорение колеса 2 в момент времени t = 2 c, если заданы закон движения рейки  и размеры колес:
и размеры колес:



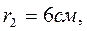


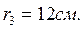
Решение
1.Рейка 4 совершает поступательное движение по закону 
Определим скорость движения рейки  .
.
При 

Ускорение рейки найдем из выражения  .
.
Знак ускорения не совпадает со знаком скорости, следовательно, рейка движется замедленно.
2. Точка К, лежащая на ободе колеса  , движется со скоростью,
, движется со скоростью,
равной скорости рейки, находящейся в зацеплении с колесом, то есть

Учитывая, что  , определим угловую скорость колеса 1:
, определим угловую скорость колеса 1:
 .
.
При 
 .
.
3. Определим угловое ускорение колеса 1:
 .
.
Ускорение точки А ступенчатого колеса 1 найдем из выражения : 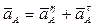
где  ;
;
 .
.
И тогда  .
.

Рисунок 6
4. Колеса радиусов  и
и  связаны бесконечным ремнем. При отсутствии проскальзывания скорости всех точек ремня одинаковы, то есть
связаны бесконечным ремнем. При отсутствии проскальзывания скорости всех точек ремня одинаковы, то есть
 а угловые скорости и угловые ускорения валов 1 и 2 обратно пропорциональны радиусам колес:
а угловые скорости и угловые ускорения валов 1 и 2 обратно пропорциональны радиусам колес:
 ;
; 
Скорость точки В, расположенной на колесе 2, рассчитываем по формуле
 .
.
5. Колеса радиусов  и
и  находятся в зацеплении друг с другом, поэтому угловую скорость и угловое ускорение колеса 3 найдем из соотношений
находятся в зацеплении друг с другом, поэтому угловую скорость и угловое ускорение колеса 3 найдем из соотношений
 ;
;  .
.
Скорость точки С, расположенной на колесе 3, находим по формуле  .
.
5.Ускорение груза 5 равно касательному ускорению точки N колеса 3:
 .
.
6. Найденные параметры движения точек и звеньев механизма изображаем на рисунке (рисунок 6).
Таблица 3
| Номер схемы | Радиусы ступеней колёс, м | Закон движения тела | |||||

| 
| 
| 
| 
| 
| ||
| 0,2 | 0,1 | 0,5 | 0,4 | 0,3 | 0,2 |  t-2t t-2t 
| |
| 0.3 | 0.1 | 0.4 | 0.3 | 0.2 | 0.1 | 
| |
| 0.4 | 0.2 | 0.4 | 0.1 | 0.3 | 0.2 | 
| |
| 0.3 | 0.2 | 0.3 | 0.1 | 0.5 | 0.3 | 
| |
| 0.4 | 0.2 | 0.4 | 0.3 | 0.5 | 0.4 | 
| |
| 0.5 | 0.4 | 0.2 | 0.1 | 0.3 | 0.2 | 
| |
| 0.3 | 0.2 | 0.5 | 0.4 | 0.4 | 0.2 | 
| |
| 0.8 | 0.6 | 0.2 | 0.1 | 0.3 | 0.2 | 
| |
| 0.3 | 0.2 | 0.4 | 0.3 | 0.4 | 0.3 | 
| |
| 0.9 | 0.8 | 0.4 | 0.3 | 0.3 | 0.2 | 
| |
| 0.6 | 0.3 | 0.5 | 0.3 | 0.3 | 0.2 |  
| |
| 0.4 | 0.2 | 0.4 | 0.3 | 0.3 | 0.2 | 
| |
| 0.2 | 0.1 | 0.4 | 0.3 | 0.5 | 0.4 | 
| |
| 0.5 | 0.3 | 0.4 | 0.3 | 0.3 | 0.2 | 
| |
| 0.3 | 0.2 | 0.6 | 0.5 | 0.3 | 0.2 | 
| |
| 0.2 | 0.1 | 0.5 | 0.4 | 0.4 | 0.3 | 
| |
| 0.3 | 0.2 | 0.4 | 0.3 | 0.6 | 0.5 | 
| |
| 0.7 | 0.3 | 0.3 | 0.1 | 0.4 | 0.2 | 
| |
| 0.6 | 0.3 | 0.4 | 0.3 | 0.4 | 0.2 | 
| |
| 0.6 | 0.5 | 0.4 | 0.3 | 0.4 | 0.1 | 
| |
| 0.4 | 0.3 | 0.2 | 0.1 | 0.7 | 0.5 | 
| |
| 0.2 | 0.1 | 0.6 | 0.5 | 0.4 | 0.3 | 
| |
| 0.6 | 0.3 | 0.2 | 0.1 | 0.3 | 0.2 | 
| |
| 0.3 | 0.2 | 0.8 | 0.6 | 0.4 | 0.3 | 
| |
| 0.5 | 0.4 | 0.5 | 0.2 | 0.8 | 0.6 | 
| |
| 0.7 | 0.6 | 0.3 | 0.1 | 0.4 | 0.3 | 
| |
| 0.8 | 0.6 | 0.3 | 0.2 | 0.4 | 0.3 | 
| |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.5 | 0.3 | 
| |
| 0.9 | 0.7 | 0.2 | 0.1 | 0.3 | 0.2 | 
| |
| 0.2 | 0.1 | 0.1 | 0.9 | - | - | 
|

Рисунок 7

Рисунок 8

Рисунок 9

Рисунок 10

Рисунок 11