Геометрическая интерпретация симплекс-метода.

Фундаментом универсального метода решения задач линейного программирования, который называется симплекс-методом, является метод направленного перебора. (По латыни симплекс означает — простои, что в данном случае интерпретируется как простой выпуклый многогранник.)
Геометрическая интерпретация симплекс-метода состоит в последовательном переходе от одной вершины многогранника к другой (от первоначально выбранной вершины к одной из соседних вершин, а именно к той, у которой линейная функция принимает лучшее или, по крайней мере, не худшее значение). Этот процесс происходит до тех пор, пока не будет найдено оптимальное решение — вершина, где достигается оптимальное значение функции (если задача имеет конечный оптимум).

 

26. Критерий оптимальности. Возможность решения задач с различными целевыми функциями в одной и той же области допустимых решений. Случай многокритериальных задач.

Критерий оптимальности (критерий оптимизации) — характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть максимальное удовлетворение поставленным требованиям. В одной задаче может быть установлено несколько критериев оптимальности.

Все факторы, входящие в описание процесса, можно разделить на две группы:

av а2,... - постоянные факторы (условия проведения операции), на которые мы влиять не можем.

xv х2,... - зависимые факторы (элементы решения).

Критерий эффективности, выражаемый целевой функцией Z, зависит от факторов обеих групп:

Z = f(a1, а2,..., xv х2,...).

Требуется найти решение (х/, х2*,..., хп*), удовлетворяющие системе неравенств (уравнений) ф,- (Ху х2,..., хп) < Ь„ / = 1, 2,..., т и обращающие в максимум (или минимум) целевую функцию, т.е. Z = f(xv х2,..., хп) ->max (min).

Многокритериальные задачи ЭММ

Подход 1. Сведение к задаче с одним критерием эффективности.

•Критерии располагаются в порядке убывания приоритетов f^x), f2(x),..., fn(x) (х - условный аргумент). В качестве целевой функции выбирается критерий, обладающий наиболее высоким приоритетом -f^x).

•Рассматривается комбинация («свертка») критериев

f (х) = ш^х) + U)2f2(x) + ... + U)nfn(x), где ы1; ш2,..., ып - некоторые коэффициенты (веса).

Подход 2. Из множества допустимых решений отбрасываются заведомо неудачные решения, уступающие другим по всем критериям. В результате остаются эффективные (или «паретовские») решения, множество которых (множество Парето) обычно существенно меньше исходного. Окончательный выбор «компромиссного» решения осуществляет Л ПР.

27. Линейная и нелинейная регрессия

Линейная регрессия

Линейная регрессия предполагает, что функция 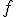зависит от параметров линейно. При этом линейная зависимость от свободной переменной необязательна,

В случае, когда функция линейная регрессия имеет вид

здесь 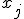— компоненты вектора .

Значения параметров в случае линейной регрессии находят с помощью метода наименьших квадратов. Использование этого метода обосновано предположением о гауссовском распределении случайной переменной.

Нелинейная регрессия.

Нелинейные регрессионные модели — модели вида

которые не могут быть представлены в виде скалярного произведения

где — параметры регрессионной модели, — свободная переменная из пространства , — зависимая переменная, 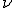— случайная величина и — функция из некоторого заданного множества.

28. Матрица (математическая модель) открытой транспортной задачи. Условный потребитель (получатель). Характеристика задач, решаемых этим методом.

Исходные данные задачи могут быть представлены в виде:

§ вектора А=(a₁,a₂,...,a_m) запасов поставщиков

§ вектора B=(b₁,b₂,...,b_n) запросов потребителей

§ матрицы стоимостей (С):

;

Переменными (неизвестными) транспортной задачи являются x_ij , i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю.
Эти переменные могут быть записаны в виде матрицы перевозок.

Математическая формулировка транспортной задачи такова: найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений, условиям неотрицательности и обеспечивающие минимум целевой функции.

Область применения: Транспортные задачи линейного программирования тесно связаны с детерминированными динамическими задачами исследования операций, в том числе и с многошаговыми задачами принятия решений в условиях определенности, имеющими большое прикладное значение.

Транспортная задача (или задача прикрепления поставщиков к потребителям) явилась одним из первых примеров оптимизации на линейных сетях. Задача стала типовой для промышленных фирм, имеющих несколько предприятий, складов, рынков сбыта или оптовых баз. Модель главным образом применяется при решении плановых задач. В этом случае стратегические решения сводятся к выбору транспортных маршрутов, по которым продукция различных предприятий доставляется на несколько складов или в различные конечные пункты назначения.

29. Множественная регрессия

Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.

Вид множественной линейной модели регрессионного анализа:

Y = b₀ + b₁x_i1 + ... + b_jx_ij + ... + b_kx_ik + e_i

где e_i - случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.

Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной.

Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии b_j показывает, на какую величину в среднем изменится результативный признак Y, если переменную X_j увеличить на единицу измерения, т. е. является нормативным коэффициентом.

Матричная запись множественной линейной модели регрессионного анализа:

Y = Xb + e

где Y - случайный вектор - столбец размерности (n x 1) наблюдаемых значений результативного признака (y₁, y₂,..., y_n);
X - матрица размерности [n x (k+1)] наблюдаемых значений аргументов;
b - вектор - столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели;
e - случайный вектор - столбец размерности (n x 1) ошибок наблюдений (остатков).

На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.

Задачи регрессионного анализа
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии b₀, b₁,..., b_k. Задачи регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным для переменных X_i и Y:

· получить наилучшие оценки неизвестных параметров b₀, b₁,..., b_k;

· проверить статистические гипотезы о параметрах модели;

· проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).

Построение моделей множественной регрессии состоит из следующих этапов:

1. выбор формы связи (уравнения регрессии);

2. определение параметров выбранного уравнения;

3. анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование уравнения.

Множественная регрессия:

· Множественная регрессия с одной переменной

· Множественная регрессия с двумя переменными

· Множественная регрессия с тремя переменными

30. Моделирование одномерных временных рядов. Основные элементы временного ряда

Временной ряд – набор чисел, привязанный к последовательным, обычно равноотстоящим моментам времени.

Уровни (или элементы) временного ряда – числа, составляющие временной ряд и полученные в результате наблюдения за ходом некоторого процесса.

Две основные цели анализа временных рядом:

· Определение природы ряда (выделение детерминированной и случайной составляющих, оценка их параметров)

· Использование полученных оценок для целей прогнозирования

 

Выявление структуры временного ряда

· При наличии во временном ряде тенденции и цикоических колебаний значения каждого последующего уровня ряда зависят от предыдущих.

· Корреляционную зависимоть между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

· Количественно автокорреляцию можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

· Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений уменьшается.

31. Моделирование сезонных и циклических колебаний. Аддитивная и мультипликативная модель временного ряда. Процесс построения модели.

32. Неопределенность системы уравнений математической модели балансового метода планирования и способы ее преодоления. Возможные варианты расчета на примере межотраслевого баланса при математическом моделировании проблемы. Преимущества и недостатки вариантов.

 

Предположим, что известны коэффициенты прямых затрат, тогда система (1) будет содержать n уравнений и 2n переменных. Такая система является неопределенной и имеет бесконечное множество решений. Для нахождения решения системы нужно задаться значениями любых n неизвестных, тогда значения остальных n неизвестных будут определяться однозначно из решения системы (1).

Возможны 3 варианта расчета:

1) Заданы валовые уровни производства всех отраслей, тогда в результате решения мы находим конечную продукцию в каждой отрасли.

2) Заданы конечные объемы продукции, тогда находим валовые выпуски продукции.

3) задана часть валовых и часть конечных выпусков, а находим остальные. Каждый из вариантов имеет положительные и отрицательные стороны.

Стороны: если мы рассматриваем первый вариант, то в результате находим конечную продукцию, которая может не соответствовать нашим потребностям. Если рассмотрим второй вариант, то некоторые отрасли могут быть не в состоянии производить такие выпуски продукции. Поэтому чаще всего используется третий вариант, при этом задаются уровни пр-ва нужных мощностей.

 

33. Общая формулировка задачи линейного программирования (ЗЛП). Каноническая форма ЗЛП.

Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁ , х₂ , … х_n ) и функция этих переменных f(x) = f (х₁ , х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х₁ , х₂ , … х_n
б) область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в себя:

· максимум или минимум целевой функции (критерий оптимальности);

· систему ограничений в форме линейных уравнений и неравенств;

· требование неотрицательности переменных.