Графическая интерпретация ЗЛП
1. Построить область допустимых решений, в которых одновременно удовлетворяются все ограничения
2. На график наносят ряд параллельных прямых, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях целевой функции.
3. Определяется наклон целевой функции направление, в котором происходит увеличение.
4. Перемещаем прямую целевой функции в направлении возрастания до тех пор, пока она не сместиться в область недопустимых решений.
5. Определим последнюю точку касания прямой и допустимой области решения. Находим координаты этой точки, решая систему двух уравнений, на пересечении которых лежит данная точка.
6. Вычисляем значения целевой функции в этой точке.
Случаи при графическом решении ЗЛП:
1. Линия уровня параллельна некоторой стороне многоугольника (ОДР). В этом случае каждая угловая точка этой стороны многоугольника и любая точка между ними является оптимальным решением ЗЛП (бесконечное множество решений).
2. ОДР является неограниченной, целевая функция на ОДР не ограничена сверху (задача на max не имеет решения).
3. Система ограничений несовместима, ОДР есть пустое множество (ЗЛП не имеет решения).
8. Граф-аналитический метод решения ЗЛП. Геометрическая интерпретация и графическое решение ЗЛП.

Схема решения задачи симплексным методом состоит из трёх основных элементов:
1) указывается способ вычисления первоначального допустимого решения задачи;
2) при помощи признака оптимальности проверяется, не является ли это решение оптимальным.
3) По выбранному начальному решению строятся другие решения, более близкие к оптимальному.
Доказано, что таким путем через конечное число шагов (итераций) можно получить оптимальное решение задачи. В ходе решения задачи симплекс-методом можно установить является ли задача разрешимой.
Геометрически ЗЛП представляет собой отыскание в многоугольнике решений такой угловой точки, координаты которой дают максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений.
Графическое решение ЗЛП:
1. Построить область допустимых решений, в которых одновременно удовлетворяются все ограничения
2. На график наносят ряд параллельных прямых, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях целевой функции.
3. Определяется наклон целевой функции направление, в котором происходит увеличение.
4. Перемещаем прямую целевой функции в направлении возрастания до тех пор, пока она не сместиться в область недопустимых решений.
5. Определим последнюю точку касания прямой и допустимой области решения. Находим координаты этой точки, решая систему двух уравнений, на пересечении которых лежит данная точка.
6. Вычисляем значения целевой функции в этой точке.
| 9. Граф-аналитический метод решения ЗЛП. Область допустимых решений. Особые случаи в области допустимых решений. Схема решения задачи симплексным методом состоит из трёх основных элементов: 1) указывается способ вычисления первоначального допустимого решения задачи; 2) при помощи признака оптимальности проверяется, не является ли это решение оптимальным. 3) По выбранному начальному решению строятся другие решения, более близкие к оптимальному. Доказано, что таким путем через конечное число шагов (итераций) можно получить оптимальное решение задачи. В ходе решения задачи симплекс-методом можно установить является ли задача разрешимой. Геометрически ЗЛП представляет собой отыскание в многоугольнике решений такой угловой точки, координаты которой дают максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений. В ЗЛП область допустимых решений всегда является выпуклым множеством, т.е. таким множеством, что наряду с любыми двумя точками, принадлежащими этому множеству, этому же множеству принадлежит и отрезок, соединяющий эти две точки. 1. Линия уровня параллельна некоторой стороне многоугольника (ОДР). В этом случае каждая угловая точка этой стороны многоугольника и любая точка между ними является оптимальным решением ЗЛП (бесконечное множество решений). 2. ОДР является неограниченной, целевая функция на ОДР не ограничена сверху (задача на max не имеет решения). 3. Система ограничений несовместима, ОДР есть пустое множество (ЗЛП не имеет решения). |
10. Граф-аналитический метод решения ЗЛП. Типы уравнений-ограничений при решении экономических проблем и их графическое отображение. Случай множества равноценных оптимальных планов.
Случай множества равноценных планов: если F(max)||ВС, то любая точка, лежащая на отрезке ВС является оптимальным планом, включая точки В и С.
 Типы уравнении-ограничении
Тип 1 (ограничение сверху), - ограничение по ресурсам:
а1х1+ а2х2+... + апхп<Ак,
Xj-объем производства какого-то товара / (/ = 1, 2,...,п).
Ак- количество ресурса типа к (к = 1,2,..., т); а - норма расхода этого ресурса при производстве товара /'.
Тип 2 (ограничение снизу), - задание (план) по производству:
а1х1+ а2х2+... + апхп>Ак.
Если а1 = а2 = ... = on = 1, то
Ак - план производства продукции к(к = 1,2,..., т), а х1х2,хп - варианты технологий. Тип 3 (равенство). а1х1 + а2х2 + ... + апхп = Ак,
Если о, = 1, то условие характеризует какое-то отношение в материальном потоке.
Если а1 = а2 = ... = an = 1, то условием может быть строго заданный план производства
Если математическая модель задачи линейного программирования имеет вид:
Типы уравнении-ограничении
Тип 1 (ограничение сверху), - ограничение по ресурсам:
а1х1+ а2х2+... + апхп<Ак,
Xj-объем производства какого-то товара / (/ = 1, 2,...,п).
Ак- количество ресурса типа к (к = 1,2,..., т); а - норма расхода этого ресурса при производстве товара /'.
Тип 2 (ограничение снизу), - задание (план) по производству:
а1х1+ а2х2+... + апхп>Ак.
Если а1 = а2 = ... = on = 1, то
Ак - план производства продукции к(к = 1,2,..., т), а х1х2,хп - варианты технологий. Тип 3 (равенство). а1х1 + а2х2 + ... + апхп = Ак,
Если о, = 1, то условие характеризует какое-то отношение в материальном потоке.
Если а1 = а2 = ... = an = 1, то условием может быть строго заданный план производства
Если математическая модель задачи линейного программирования имеет вид:
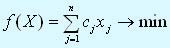 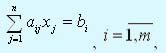 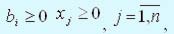
|
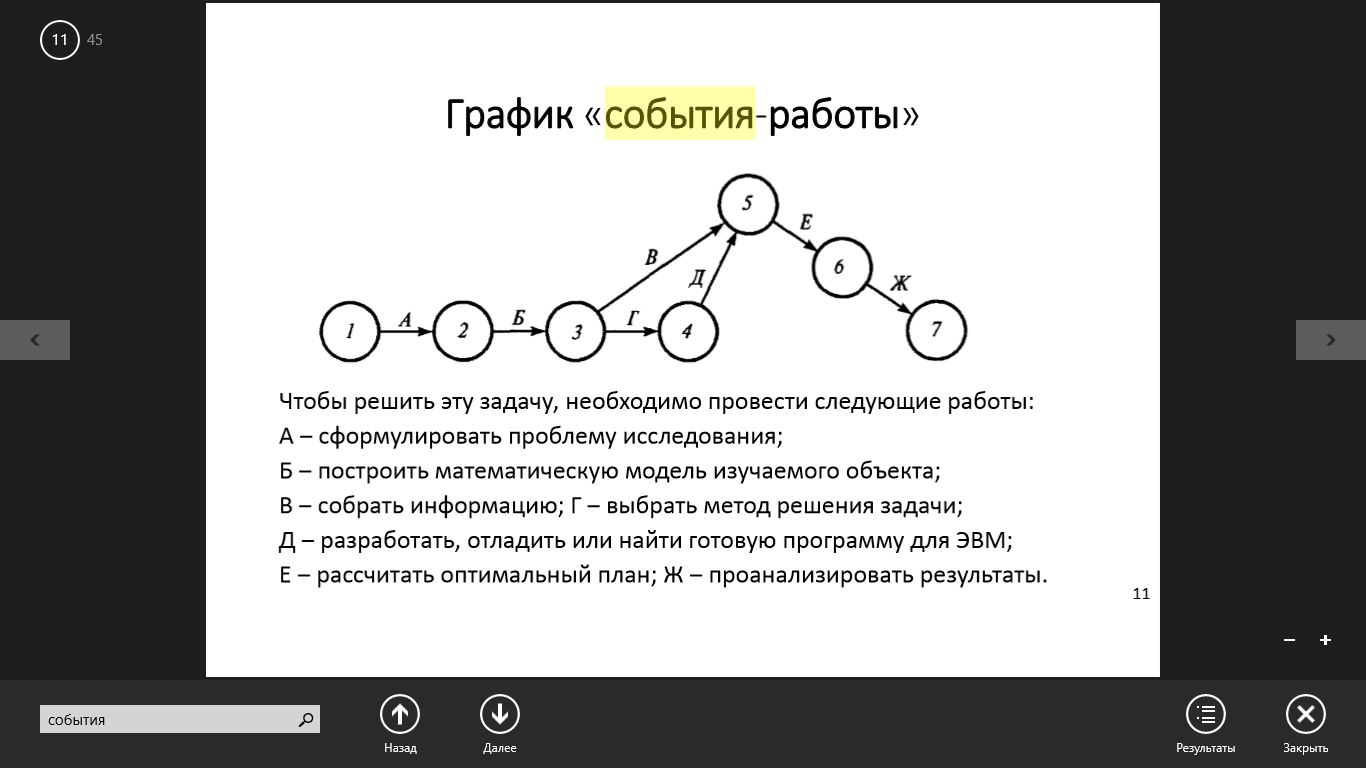
11. Два типа графиков, используемых в сетевых моделях: «событие-работы», «работы-связи». Их преимущества и недостатки.

|
12. Двойственная задача линейного программирования. Взаимосвязи прямой и двойственной задачи. Двойственная задача со смешанными ограничениями.
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной по отношению к исходной. Понятие двойственности взаимно. Теория двойственности позволяет провести полезные качественные исследования задач линейного программирования. В зависимости от вида исходной задачи различают симметричную, несимметричную и смешанные пары двойственных задач. Когда система ограничений одной из задач содержит как уравнения, так и неравенства, и некоторые переменные неотрицательны, то пара двойственных задач называется смешанной.
Связь между решениями прямой и двойственной задач
Рассмотрим пару двойственных задач, образованную основной задачей линейного программирования и двойственной к ней. Исходная задача: найти максимум функции:  (43) при условиях (43) при условиях  (44) (44) 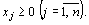 (45) Двойственная задача: найти минимум функции: (45) Двойственная задача: найти минимум функции:  (46) при условиях (46) при условиях 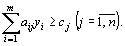 (47)
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1. Если Х – некоторый план исходной задачи (43) – (45), a Y – произвольный план двойственной задачи (46), (47), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т. е. (47)
Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже леммами и теоремами двойственности.
Лемма 1. Если Х – некоторый план исходной задачи (43) – (45), a Y – произвольный план двойственной задачи (46), (47), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т. е.  Лемма 2. Если
Лемма 2. Если  для некоторых планов X* и Y* задач (43) – (45) и (46), (47), то X* – оптимальный план исходной задачи, а Y* – оптимальный план двойственной задачи.
Теорема 8 (первая теорема двойственности). Если одна из задач двойственной пары (43) – (45) или (46), (47) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е. для некоторых планов X* и Y* задач (43) – (45) и (46), (47), то X* – оптимальный план исходной задачи, а Y* – оптимальный план двойственной задачи.
Теорема 8 (первая теорема двойственности). Если одна из задач двойственной пары (43) – (45) или (46), (47) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т. е.  Если же целевая функция одной задачи из двойственной пары неограничена (для исходной (43) – (45) – сверху, для двойственной (46), (47) – снизу), то другая задача вообще не имеет планов.
Теорема 9 (вторая теорема двойственности). План Если же целевая функция одной задачи из двойственной пары неограничена (для исходной (43) – (45) – сверху, для двойственной (46), (47) – снизу), то другая задача вообще не имеет планов.
Теорема 9 (вторая теорема двойственности). План 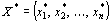 задачи (43) – (45) и план задачи (43) – (45) и план  задачи (46), (47) являются оптимальными планами этих задач тогда и только тогда, когда для любого задачи (46), (47) являются оптимальными планами этих задач тогда и только тогда, когда для любого  выполняется равенство выполняется равенство

|
13. Двойственная задача линейного программирования. Построение двойственных задач и их свойства.
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной по отношению к исходной. Понятие двойственности взаимно. Теория двойственности позволяет провести полезные качественные исследования задач линейного программирования. В зависимости от вида исходной задачи различают симметричную, несимметричную и смешанные пары двойственных задач.
Рассмотрим правила составления двойственных задач.
Симметричная пара
1. В исходной задаче знаки неравенств системы m ограничений приводятся к единому виду: «≤» в задаче на максимум и «≥» в задаче на минимум.
2. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная yi, i=1, 2, …m.
3. Составляется целевая функция Z от переменных yi (i=1, 2, …m), коэффициентами которой будут свободные члены системы ограничений исходной задачи. Цель меняется на противоположную.
4. Составляется система ограничений двойственной задачи. Матрицу коэффициентов системы ограничений двойственной задачи получают транспонированием матрицы коэффициентов исходной задачи. Знаки неравенств системы ограничений двойственной задачи противоположны знакам неравенств в исходной задаче. Свободными членами неравенств системы ограничений являются коэффициенты целевой функции исходной задачи. Переменные yi(i=1, 2, …m) неотрицательны.
Свойства:
1. Если целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в ограничениях приводят к виду “  ”, а в задаче на минимум – вид “ ”, а в задаче на минимум – вид “ 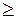 ”.
2. Матрица, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица в двойственной задаче являются транспонированными по отношению друг к другу.
3. Число переменных в двойственной задаче равно числу ограничений исходной задачи, а число ограничений двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи.
5. Правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи.
6. Предполагается, что переменные в обеих задачах являются неотрицательными. ”.
2. Матрица, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица в двойственной задаче являются транспонированными по отношению друг к другу.
3. Число переменных в двойственной задаче равно числу ограничений исходной задачи, а число ограничений двойственной задачи – числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи.
5. Правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи.
6. Предполагается, что переменные в обеих задачах являются неотрицательными.
|
14. Двойственная задача линейного программирования. Характеристика основных соотношений оптимальных планов двойственной пары.
Каждой задаче линейного программирования соответствует другая задача, называемая двойственной по отношению к исходной. Понятие двойственности взаимно. Теория двойственности позволяет провести полезные качественные исследования задач линейного программирования.
Двойственная задача составляется согласно следующим правилам: 1. Целевая функция исходной задачи задается на максимум, а целевая функция двойственной – на минимум. 2. Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу. 3. Коэффициенты  целевой функции прямой задачи являются свободными членами ограничений двойственной задачи. 4. Свободные члены целевой функции прямой задачи являются свободными членами ограничений двойственной задачи. 4. Свободные члены 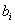 ограничений прямой задачи являются коэффициентами целевой функции двойственной. 5. Если прямая задача на максимум, то ее система ограничений представляется в виде неравенств типа ограничений прямой задачи являются коэффициентами целевой функции двойственной. 5. Если прямая задача на максимум, то ее система ограничений представляется в виде неравенств типа 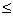 . Двойственная задача решается на минимум, и ее система ограничений имеет вид неравенств типа . Двойственная задача решается на минимум, и ее система ограничений имеет вид неравенств типа  . 6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой. 7. Все переменные в обеих задачах неотрицательны.
Теорема.Для любых допустимых планов . 6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой. 7. Все переменные в обеих задачах неотрицательны.
Теорема.Для любых допустимых планов 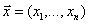 и и 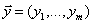 прямой и двойственной ЗЛП справедливо неравенство прямой и двойственной ЗЛП справедливо неравенство 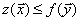 , т.е. , т.е.  (2.29) – основное неравенство теории двойственности. Теорема (критерий оптимальности Канторовича). Если для некоторых допустимых планов (2.29) – основное неравенство теории двойственности. Теорема (критерий оптимальности Канторовича). Если для некоторых допустимых планов  и и 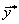 пары двойственных задач выполняется неравенство пары двойственных задач выполняется неравенство 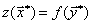 , то , то  и и 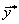 являются оптимальными планами соответствующих задач.
Теорема (малая теорема двойственности). Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них. Теорема. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: являются оптимальными планами соответствующих задач.
Теорема (малая теорема двойственности). Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них. Теорема. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: 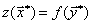 . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Теорема (о дополняющей нежесткости)Для того, чтобы планы . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Теорема (о дополняющей нежесткости)Для того, чтобы планы  и и 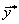 пары двойственных задач были оптимальны, необходимо и достаточно выполнение условий: пары двойственных задач были оптимальны, необходимо и достаточно выполнение условий:  (2.30) (2.30) 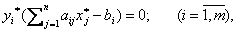 (2.31) Условия (2.30), (2.31) называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Теорема (об оценках). Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее (2.31) Условия (2.30), (2.31) называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Теорема (об оценках). Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее  (2.32) (2.32)
|
| 15. Задача булевского программирования и области применения этого класса задач в экономике. Основные этапы решения целочисленных задач методом Р.Гомори. К частному случаю задачи целочисленного линейного программирования относятся задачи, где переменные могут принимать всего лишь два значения - 0 и 1. Соответствующие задачи часто называют задачамибулевского программирования. Наиболее известные из этих задач - это задача о назначениях (какого работника на какую работу поставить), задача выбора маршрута (задача коммивояжера, задача почтальона), задача о максимальном паросочетании и т.д. Для решения задач этого типа разрабатываются очень специфические алгоритмы, основанные на комбинаторике, графах и т.д. Наиболее известные из этих задач - это задача о назначениях (какого работника на какую работу поставить), задача выбора маршрута (задача коммивояжера, задача почтальона), задача о максимальном паросочетании и т.д Целочисленное линейное программирование ориентировано на решение задач линейного программирования, в которых все или некоторые переменные принимают целочисленные значения. Для решения целочисленной задачи линейного программирования Р. Гомори предложил метод отсечения плоскостей в 1958 г. Алгоритм Гомори содержит этапы: Этап 1. Решение непрерывной задачи. Если решение дробное переход на 2 этап. Этап 2. Решение расширенной задачи. |
16. Каноническая форма задачи линейного программирования. Построение канонической формы ЗЛП.
Каноническая форма ЗЛП - задача линейного программирования вида ax = b где a - матрица коэффициентов, b - вектор ограничений. Пример: 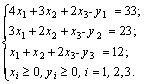 В каждой задаче ЛП ищутся значения переменных при условии, чтобы:
· эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
· при этих значениях целевая функция обращалась бы в минимум или максимум.
Одним из универсальных методов ЛП является симплексный метод, который, однако, можно применять, если задача ЛП имеет каноническую форму.
Определение. Задача ЛП имеет каноническую форму, если все ограничения системы состоят только из уравнений (кроме неравенств, выражающих неотрицательность переменных) и целевую функцию необходимо минимизировать.
Для приведения задачи к канонической форме, где все ограничения имеют вид равенств, вводят дополнительные переменные
В каждой задаче ЛП ищутся значения переменных при условии, чтобы:
· эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
· при этих значениях целевая функция обращалась бы в минимум или максимум.
Одним из универсальных методов ЛП является симплексный метод, который, однако, можно применять, если задача ЛП имеет каноническую форму.
Определение. Задача ЛП имеет каноническую форму, если все ограничения системы состоят только из уравнений (кроме неравенств, выражающих неотрицательность переменных) и целевую функцию необходимо минимизировать.
Для приведения задачи к канонической форме, где все ограничения имеют вид равенств, вводят дополнительные переменные  , которые тоже считаются неотрицательными и записывают исходную задачу в виде , которые тоже считаются неотрицательными и записывают исходную задачу в виде


т.е. в неравенстве со знаком меньше либо равно добавляютдополнительную неотрицательную переменную, а из неравенства со знаком больше либо равно вычитаютдополнительную переменную. В целевую функцию эти дополнительные переменные включают с коэффициентом 0, т.е. фактически они в целевой функции отсутствуют.
| ||||||||||||
17. Классификация взаимосвязей между признаками. Ковариация. Коэффициент корреляции. Шкала Чеддока.
Формы проявления взаимосвязей явлений и процессов весьма разнообразны. Из них в самом общем виде выделяют функциональную (полную) и корреляционную (неполную) связи.
Математически ковариация представляет собой меру линейной зависимости двух случайных величин.
Коэффициент корреляции - это математическая мера корреляции двух величин. Коэффициенты корреляции могут быть положительными и отрицательными.
Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока):
|
| 18. Классы эконометрических моделей. Схема построения эконометрических моделей. Можно выделить три основных класса эконометрических моделей, которые применяются для анализа и прогноза: регрессионные модели с одним уравнением, системы одновременных уравнений и модели временных рядов. Весь процесс эконометрического моделирования можно разбить на шесть основных этапов. · 1-й этап (постановочный) - определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли; · 2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез; · 3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными; · 4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей; · 5-й этап (идентификация модели) - статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели Непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответст-вии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели то есть предложить и реализовать математически корректную процедуру оценивания неизвестных параметров модели по имеющимся исходным данным; · 6-й этап (верификация модели) — сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных. |
19. Ковариация и коэффициент корреляции
Ковариация оценивает силу линейной зависимости между двумя числовыми переменными X и Y. Выборочная ковариация:
 Выборочный коэффициент корреляции:
Выборочный коэффициент корреляции:
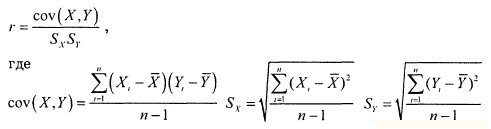 Коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к –1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (+) и обратная (–). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.
Коэффициент корреляции свидетельствует о линейной зависимости, или связи, между двумя переменными. Чем ближе коэффициент корреляции к –1 или +1, тем сильнее линейная зависимость между двумя переменными. Знак коэффициента корреляции определяет характер зависимости: прямая (+) и обратная (–). Сильная корреляция не является причинно-следственной зависимостью. Она лишь свидетельствует о наличии тенденции, характерной для данной выборки.
|
20. Корреляция, вычисление коэффициентов корреляции. Парный регрессионный анализ. Причины присутствия в модели случайной составляющей.
Корреляция - это один из основных терминов теории вероятности, показывающий меру зависимости между двумя и более случайными величинами. Данная зависимость выражается через коэффициент корреляции. Коэффициент корреляции принимает значения от -1 до +1. Чем выше значение коэффициента корреляции, тем больше зависимость между величинами. Корреляция бывает положительной и отрицательной.
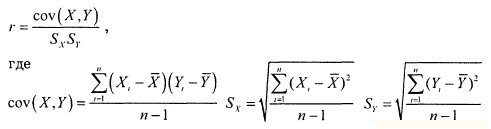 Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.
Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.
|
| 21. Коэффициент детерминации. Его назначение, интерпретация, формулы расчёта. |
Коэффициент детерминации ( - R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по признакам дисперсии зависимой переменной) в дисперсии зависимой переменной. В случае линейной зависимости
- R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по признакам дисперсии зависимой переменной) в дисперсии зависимой переменной. В случае линейной зависимости  является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели линейной регрессии с одним признаком
является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели линейной регрессии с одним признаком  коэффициент детерминации равен квадрату обычного коэффициента корреляции между
коэффициент детерминации равен квадрату обычного коэффициента корреляции между  и
и  .
.
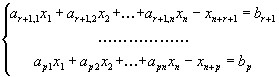
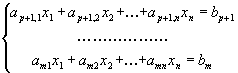
 ,
,