Алгебра событий.

Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.

Аналогично суммой конечного числа событий А₁, А₂, ..., А_k называется событие А = А₁+А₂ + ... + А_k, состоящее в наступлении хотя бы одного из событий Аi, (i = 1, ..., k).

Из определения следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А + А = А (а не 2А).

Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошли и событие А, и событие В.

Аналогично произведением конечного числа событий А1, А2, ..., Аk называется событие А = А1А2…Аk, состоящее в том, что в результате испытания произошли все указанные события.

Из определения непосредственно следует, что АВ = ВА. Справедливы также сочетательный и дистрибутивный законы. Однако АА = А (а не А²).

Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.

Рассмотрим полную группу попарно несовместимых событий А₁, А₂, ..., Аn, связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий Аi, (i = 1, 2, …, k) равновозможно, т. е. условия испытания не создают преимуществ в появлении какого-либо события перед другими возможными.

События А₁, А₂, ..., Аn, образующие полную группу попарно несовместимых и равновозможных событий, называют элементарными событиями (ω).

Событие А называется благоприятствующим событию В, если наступление события А влечет за собой наступление события В.

Классическое определение вероятности. Вероятностью Р(А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т.е.

Р(А) = m/n.

Свойства вероятности события:

1. Вероятность достоверного события равна 1. Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т.е. m = n и, следовательно, P(Ω) = m/n = n/n = 1.

2. Вероятность невозможного события равна 0. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. m = 0, откуда: P(Ø) = m/n = 0/n = 0.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае 0<m<n и, значит, 0<m/n<1. Следовательно, 0<Р(А)<1. Т.о., вероятность любого события удовлетворяет двойному неравенству: 0 ≤ Р(А) ≤ 1.

Замечание. Из определения вероятности следует, что элементарные события являются равновероятными, т. е. обладают одной и той же вероятностью.

События, вероятности которых очень малы (близки к нулю) или очень велики (близки к единице), называются соответственно практически невозможными или практически достоверными событиями.

2. Статистическое определение вероятности события и условия его применимости. Пример.

Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.

,

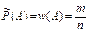Где 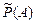- статистическая вер-ть события А; w(A) - относительная частота (частость) события А; m - число испытаний, в которых появилось событие А; n - общее число испытаний.

В отличие от «математической» вероятности Р(А), рассматриваемой в классическом определении, статистическая вер-ть 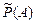является характеристикой опытной, экспериментальной. Если Р(А) есть доля случаев, благоприятствующих событию А, которая определяется непосредственно, без каких-либо испытаний, то 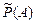есть доля тех Фактически произведенных испытаний, в которых событие А появилось.

Статистическое определение вер-ти, как и понятия и методы теории веро-тей в целом, применимы не к любым событиям с неопределенным исходом, которые в житейской практике считаются случайными, а только к тем из них, которые обладают определенными свойствами.

1) Рассматриваемые события д.б. исходами только тех испытаний, которые м.б. воспроизведены неограниченное число раз при одном и том же комплексе условий.

2) События должны обладать так называемой статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в различных сериях испытаний относительная частота (частость) события изменяется незначительно (тем меньше, чем больше число испытаний), колеблясь около постоянного числа. Оказалось, что этим постоянным числом является вероятность события. Факт приближения относительной частоты, или частости, события к его вер-ти при ­ числа испытаний, сводящихся к схеме случаев, подтверждается многочисленными массовыми экспериментами, проводимыми разными лицами со времен возникновения теории вер-тей.

3) Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вер-ть события Р(А) приближенно равной ее относительной частоте. Резюмируя, можно сказать, что теория вер-тей изучает лишь такие события, в отношении которых имеет смысл не только утверждение об их случайности, но и возможна объективная оценка относительной частоты их появления. Так, утверждение, что при выполнении определенного комплекса условий S вероятность события = р, означает не только случайность события А, но и определенную, достаточно близкую к р, долю появлений события А при большом числе испытаний; а значит, выражает определенную объективную (хотя и своеобразную) связь между комплексом условий S и событием А (не зависящую от субъективных суждений о наличии этой связи того или иного лица). И даже просто существование вероятности р (когда само значение р неизвестно) сохраняет качественно суть этого утверждения, выделенную курсивом.

Легко проверить, что свойства вер-ти, вытекающие из классического определения, сохраняются и при статистическом определении вероятности.

Замечание: 1) Статистическая вер-ь может быть найдена только после проведения опытов, а для классической вероятности опыты не нужны. 2) Статистическая вер-ть получается различной для разных серий опытов, однако при достаточно большом количестве опытов практически достоверно, что статистическая вер-ть будет сколь угодно мало отличатся от классической вер-ти (устойчивость статистической вер-ти).

3. Несовместные и совместные события. Сумма событий. Теоре­ма сложения вероятностей (с доказательством).

Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.

2 события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В. Аналогично суммой конечного числа событий А₁, А₂, ..., А_k называется событие А = А₁+А₂ + ... + А_k, состоящее в наступлении хотя бы одного из событий Аi, (i = 1, ..., k). Из определения следует, что А + В = В + А. Справедливо также и сочетательное свойство. Однако А + А = А (а не 2А).

Теорема сложения вероятностей:

Теорема. Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий: Р(А + В + ... + К) = Р(А) + Р(В) + ... + Р(К).

□ Докажем теорему для схемы случаев, рассматривая сумму двух событий.

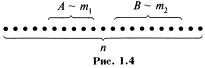
Пусть в результате испытания из общего числа n равновозможных и несовместных (элементарных) исходов испытания (случаев) событию А благоприятствует m_l случаев, а событию В ­ m₂ случаев (рис. 1.4).

Согласно классическому определению .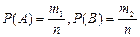

Т.к. события А и В несовместные, то ни один из случаев, благоприятствующих одному из этих событий, не благоприятствует другому (рис. 1.4). Поэтому событию А+В будет благоприятствовать m_l+ m₂ случаев. Следовательно, ■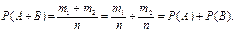

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна 1:

P(A) + P(B) + … + P(K) = 1.

□ Если события А,В,…,К образуют полную группу, то они единственно возможные и несовместные.

Т.к. события А,В,…,К – единственно возможные, то событие А + В + … +К, состоящее в появлении в результате испытания хотя бы одного из этих событий, является достоверным, то его вероятность = 1:

Р(А + В + … + К) = 1.

Т.к. события А,В,…,К – несовместные, к ним применима теорема сложения:

Р(А + В + … + К) = Р(А) + Р(В) + … + Р(К) = 1.■

Следствие 2. Сумма вероятностей противоположных событий = 1:

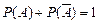
□ Утверждение следует из того, что противоположные события образуют полную группу. ■

4. Полная группа событий. Противоположные события. Соот­ношение между вероятностями противоположных событий (с вы­водом).

Несколько событий образуют полную группу событий если в результате опыта обязательно появится хотя бы одно из них. Это означает, что в результате испытания должно произойти 1 и только 1 из этих событий.

Частным случаем событий, образующих полную группу, являются противоположные события. 2 несовместимых события из которых 1 должно обязательно произойти называютсяпротивоположными.Событие противоположное событию А обозначают 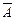.