Закон Джоуля-Ленца в интегральной и дифференциальной формах
Q = A = U × I × t = I2 × R × t. (6.15)
Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме, позволяющая вычислить количество теплоты, выделяющейся в проводнике. Для того, чтобы характеризовать тепловой эффект тока в различных точках проводника, выделим в нём элементарный участок трубки тока (рис. 6.8.). Запишем для этого элемента закон Джоуля-Ленца:
Закон Джоуля-Ленца: в интегральной форме: Q = I2 × R × t; в дифференциальной форме: Руд = 
× Е2= 
.
64 Классическая теория электропроводности металлов (теория Друде-Лоренца).
Электроны в металле рассматриваются как электронный газ, к которому можно применить кинетическую теорию газов. Считается, что электроны, как и атомы газа в кинетической теории, представляют собой одинаковые твердые сферы, которые движутся по прямым линиям до тех пор, пока не столкнутся друг с другом. Предполагается, что продолжительность отдельного столкновения пренебрежимо мала, и что между молекулами не действует никаких иных сил, кроме возникающих в момент столкновения. Так как электрон - отрицательно заряженная частица, то для соблюдения условия электронейтральности в твердом теле также должны быть частицы другого сорта - положительно заряженные. Друде предположил, что компенсирующий положительный заряд принадлежит гораздо более тяжелым частицам (ионам), которые он считал неподвижными. Во времена Друде не было ясно, почему в металле существуют свободные электроны и положительно заряженные ионы, и что эти ионы собой представляют. Ответы на эти вопросы смогла дать только квантовая теория твердого тела. Для многих веществ, однако, можно просто считать, что электронный газ составляют слабо связанные с ядром внешние валентные электроны, которые в металле "освобождаются" и получают возможность свободно передвигаться по металлу, тогда как атомные ядра с электронами внутренних оболочек (атомные остовы) остаются неизменными и играют роль неподвижных положительных ионов теории Друде.
. Несмотря на то, что плотность газа электронов проводимости примерно в 1000 раз больше плотности классического газа при нормальных температуре и давлении, и несмотря на присутствие сильного электрон-электронного и электрон-ионного взаимодействия в модели Друде для рассмотрения электронного газа в металлах почти без изменений применяются методы кинетической теории нейтральных разреженных газов.
Основные предположения теории Друде.
· В интервале между столкновениями не учитывается взаимодействие электрона с другими электронами и ионами. Иными словами, принимается, что в отсутствие внешних электромагнитных полей каждый электрон движется с постоянной скоростью по прямой линии. Далее, считают, что в присутствии внешних полей электрон движется в соответствии с законами Ньютона; при этом учитывают влияние только этих полей, пренебрегая сложными дополнительными полями, порождаемыми другими электронами и ионами. Приближение, в котором пренебрегают электрон-электронным взаимодействием в промежутках между столкновениями, известно под названием приближения независимых электронов. Соответственно приближение, в котором пренебрегают электрон-ионным взаимодействием, называется приближением свободных электронов.
· В модели Друде, как и в кинетической теории, столкновения — это мгновенные события, внезапно меняющие скорость электрона. Друде связывал их с тем, что электроны отскакивают от непроницаемых сердцевин ионов (а не считал их электрон-электронными столкновениями по аналогии с доминирующим механизмом столкновений в обычном газе).
· Предполагается, что за единицу времени электрон испытывает столкновение (т. е. внезапное изменение скорости) с вероятностью, равной 
. Имеется в виду, что для электрона вероятность испытать столкновение в течение бесконечно малого промежутка времени 
равна просто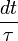 
. Время 
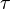называют временем релаксации, или временем свободного пробега; оно играет фундаментальную роль в теории проводимости металлов. Из этого предположения следует, что электрон, выбранный наугад в настоящий момент времени, будет двигаться в среднем в течение времени 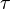до его следующего столкновения и уже двигался в среднем в течение времени 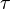с момента предыдущего столкновения. В простейших приложениях модели Друде считают, что время релаксации 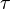не зависит от пространственного положения электрона и его скорости.
· Предполагается, что электроны приходят в состояние теплового равновесия со своим окружением исключительно благодаря столкновениям. Считается, что столкновения поддерживают локальное термодинамическое равновесие чрезвычайно простым способом: скорость электрона сразу же после столкновения не связана с его скоростью до столкновения, а направлена случайным образом, причем ее величина соответствует той температуре, которая превалирует в области, где происходило столкновение. Поэтому чем более горячей является область, где происходит столкновение, тем большей скоростью обладает электрон после столкновения
· Кинетическое уравнение Больцмана в приближении времени релаксации приводит для проводимости электронного газа к формуле Друде:
· 
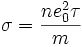
Полученная формула выражает закон Ома в дифференциальной форме. Здесь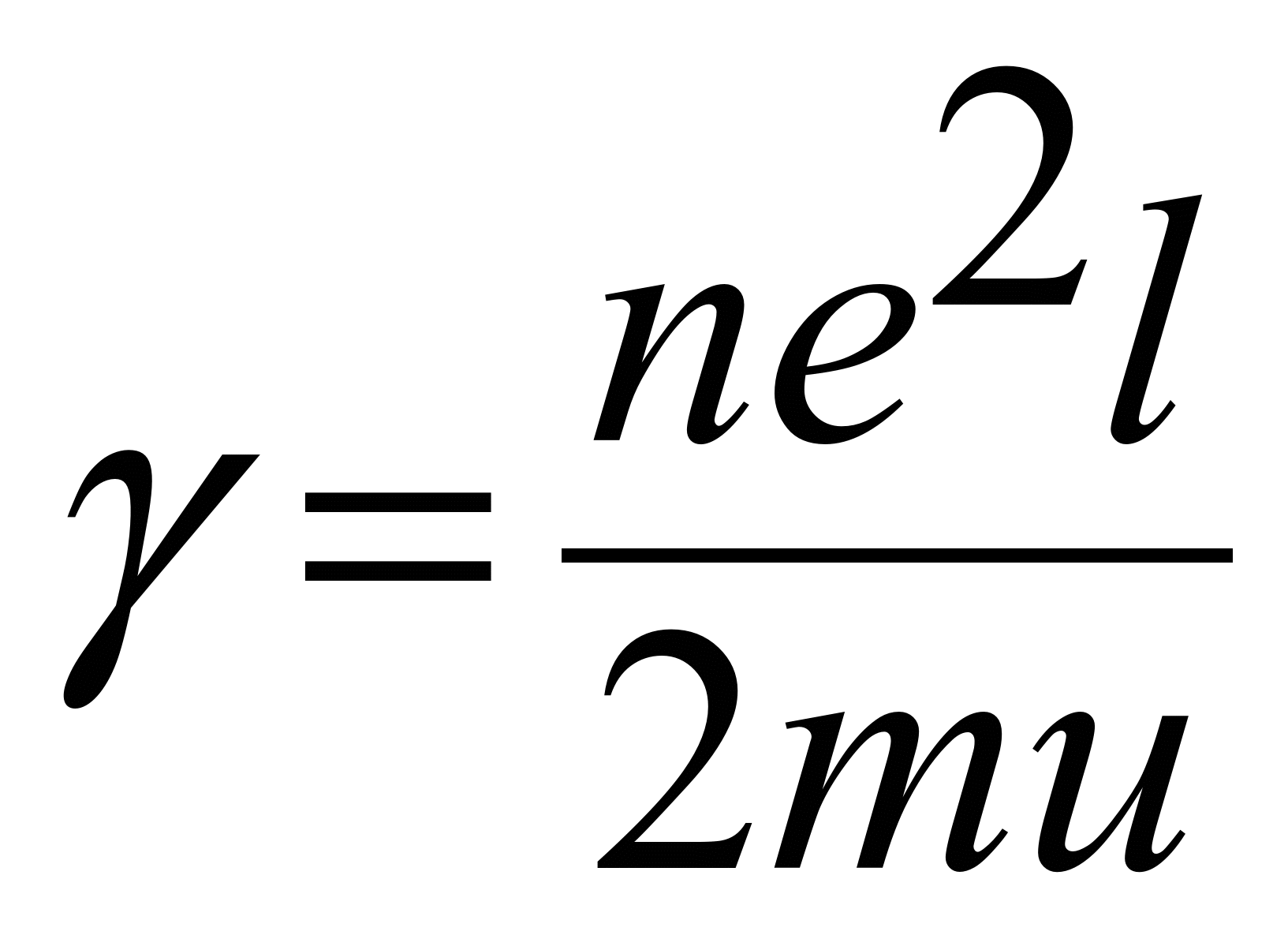 
- коэффициент пропорциональности, проводимость металла.
Если бы не было столкновений между электронами и ионами решетки, то проводимость была бы бесконечной. Определим температурную зависимость проводимости. Концентрация электронов и длина свободного пробега не должны зависеть от температуры. От температуры зависит только средняя скорость теплового движения.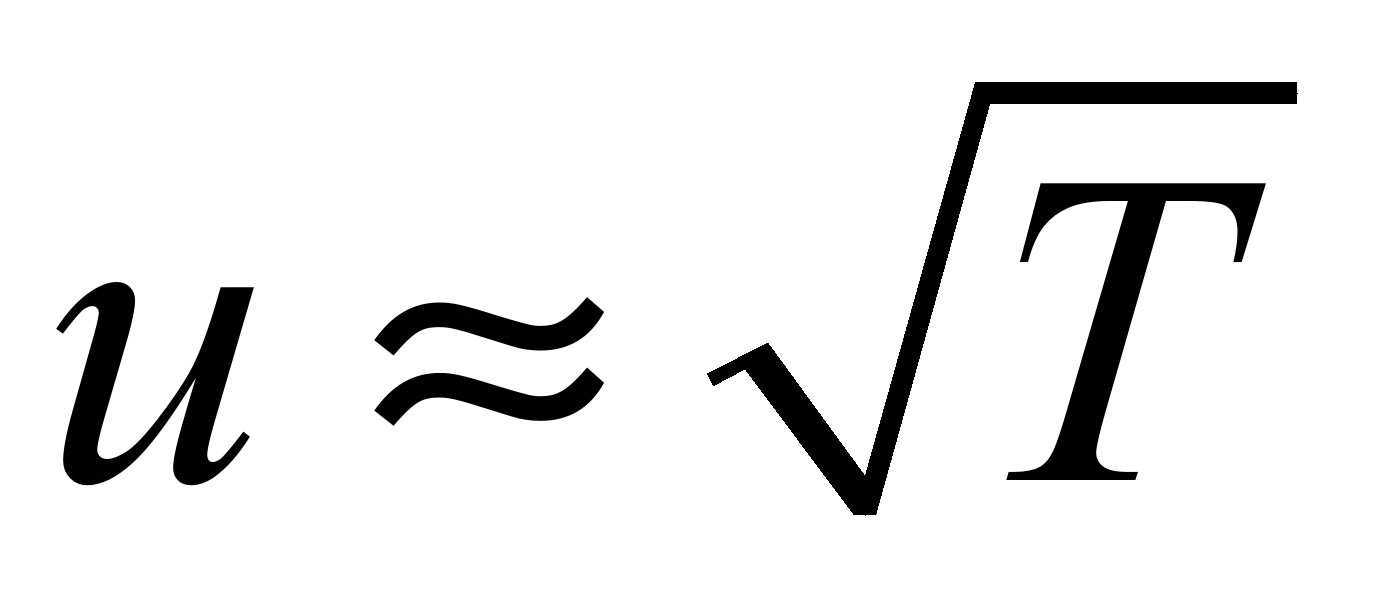 
. Следовательно, проводимость обратно пропорциональна корню из Т, а сопротивление возрастает как корень из Т. Эксперимент показывает, что сопротивление в широком интервале температур пропорционально температуре, и только при низких температура турах 
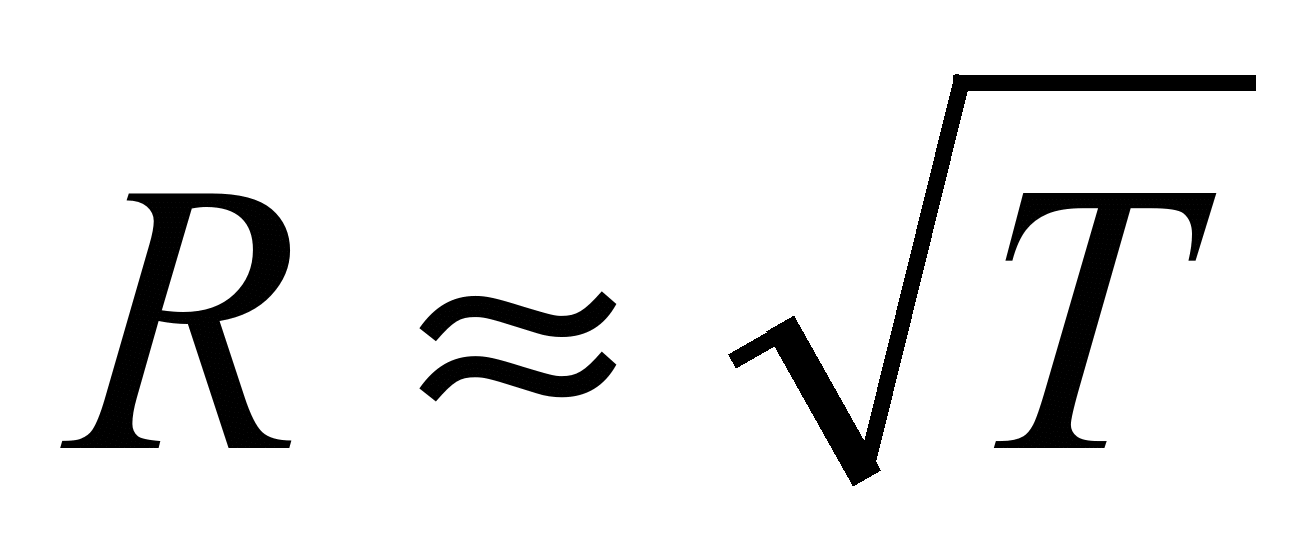. Таким образом, теория проводимости металлов Друде-Лоренца, приводя к закону Ома, не может объяснить температурной зависимости сопротивления. Объяснение может дать только квантовая теория.
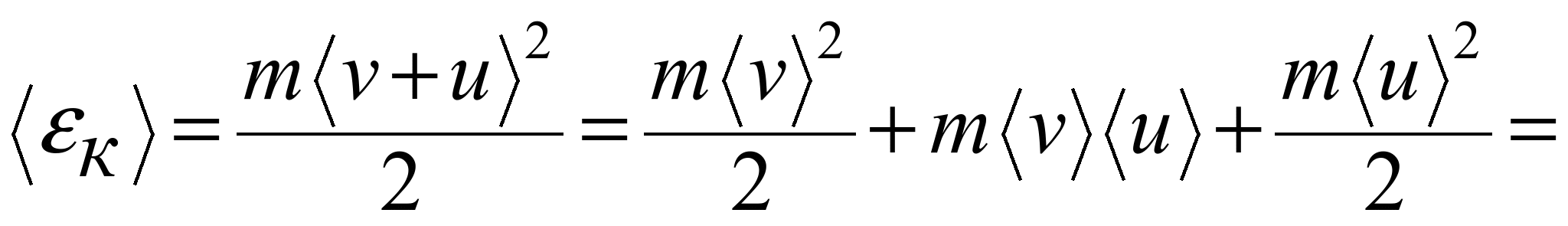
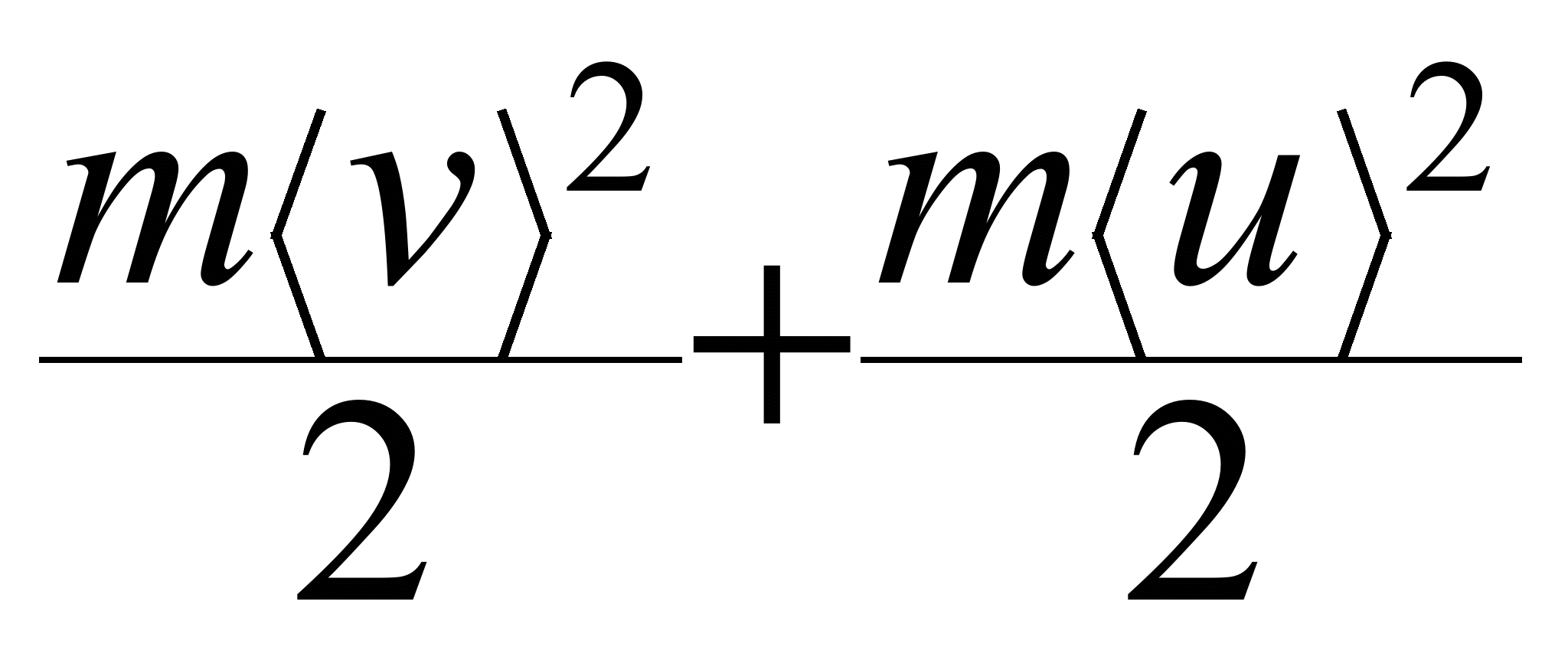, (5)
закон Джоуля-Ленца
Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
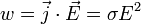
где 
— мощность выделения тепла в единице объёма, 
— плотность электрического тока, 
— напряжённость электрического поля, σ — проводимость среды.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка
В математической форме этот закон имеет вид
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2. В случае постоянных силы тока и сопротивления:
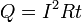
Закон Видемана–Франца. Видеман и Франц установили связь между коэффициентом теплопроводности и электропроводности для всех металлов. Теплопроводность металлов, как показывает опыт, значительно выше теплопроводности диэлектриков. Из этого следует, что теплопроводность в металлах осуществляется в основном не кристаллической решеткой, а свободными электронами. Поэтому, рассматривая электроны, как одноатомный газ, используем формулу для коэффициента теплопроводности газов: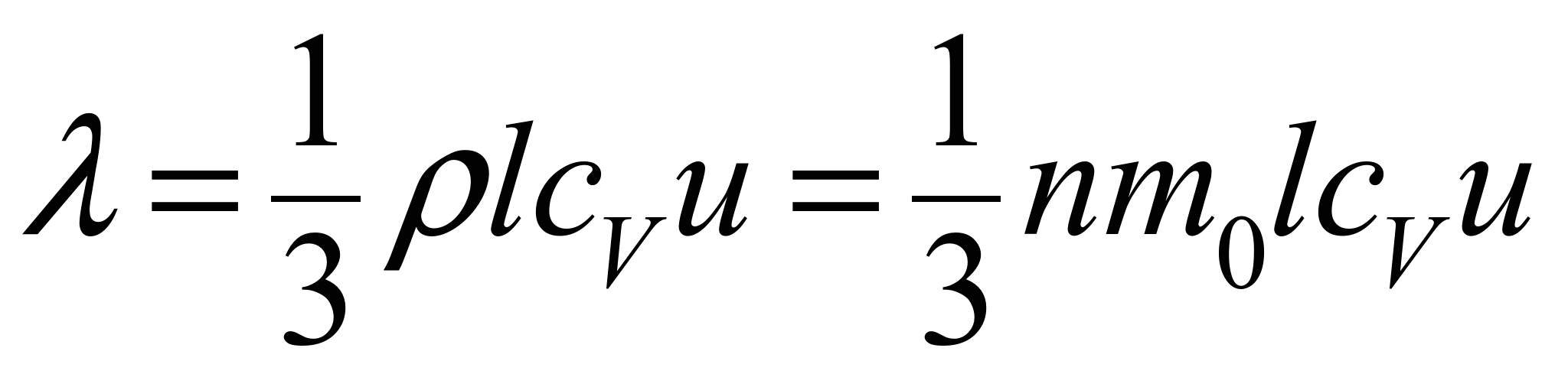 
. Удельная теплоемкость одноатомного газа: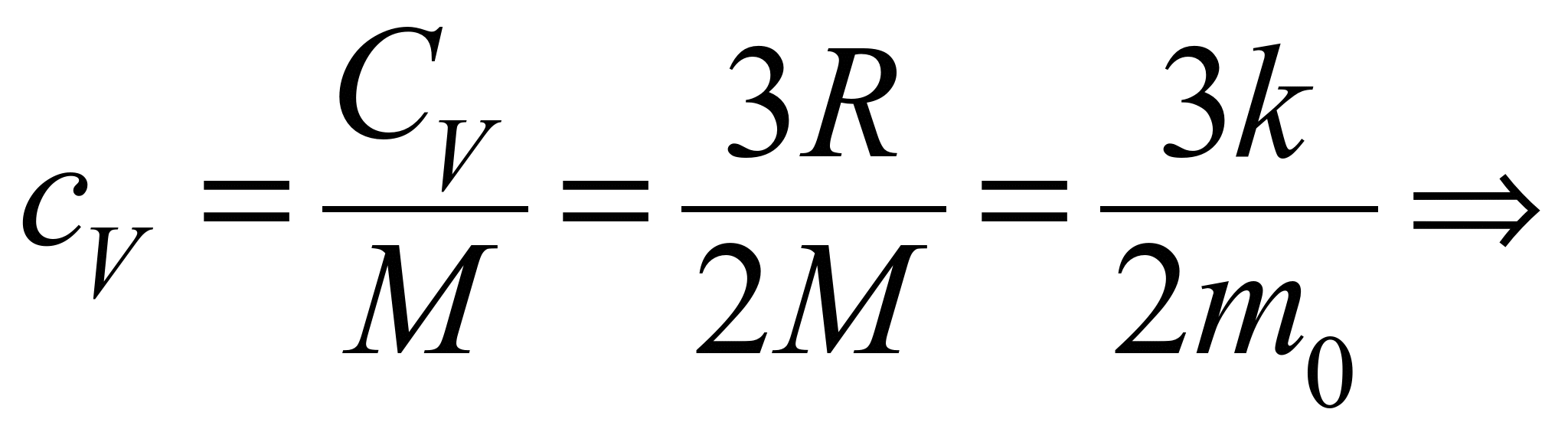 
. Отношение коэффициента теплопроводности к коэффициенту электропроводности: 
. Т.о. отношение коэффициента теплопроводности к коэффициенту электропроводности пропорционально температуре. Это соотношение хорошо согласуется с экспериментальными данными. Но уточненные Лоренцем расчеты получили другое соотношение между l и g, которое хуже согласуется с экспериментальными данными. Т.е. классическая теория дает только качественное соответствие закона Видемана –Франца.
ПЛО́ТНОСТЬ ТО́КА, векторная характеристика электрического тока (см. ЭЛЕКТРИЧЕСКИЙ ТОК) j, равная по модулю электрическому заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряженных частиц.
При равномерном распределении плотности электрического тока по сечению проводника плотность тока j будет равна отношению силы тока (см. СИЛА ТОКА) I в нем к площади его поперечного сечения S:
j = I/ S
Плотность тока характеризует силу тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока
Единицей измерения плотности тока является А/м2.
Плотность тока можно определить также следующим образом:
Так как сила тока I = nevS, где:
n — концентрация носителей заряда;
e — заряд носителей тока;
v — средняя скорость упорядоченного движения частиц;
S — площадь поперечного сечения проводника, через который течет ток,
То плотность тока J = I/ S = nev S/ S = nev.
Произведение ne характеризует плотность заряда е (заряд в единице объема), поэтому плотность электрического тока:
j =rеv.
Плотность тока величина векторная, по направлению совпадает с направлением вектора скорости v, т. е. с направлением упорядоченного движения электрических зарядов.
Плотность тока пропорциональна вектору напряженности:
j = sЕ.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.
В своей оригинальной форме он был записан его автором в виде :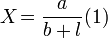 
,
Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) 
, l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].
В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает
Закон Ома для полной цепи:
, (2)
где:
· — ЭДС источника напряжения(В),
· 
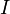— сила тока в цепи (А),
· 
— сопротивление всех внешних элементов цепи (Ом),
· 
— внутреннее сопротивление источника напряжения (Ом).
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле. Открыт Эдвином Холлом в 1879 году в тонких пластинках золота.
В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле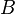 
течёт электрический ток под действием напряжённости 
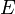. Магнитное поле будет отклонять носители заряда (для определённости электроны) от их движения вдоль или против электрического поля к одной из граней бруса. При этом критерием малости[1] будет служить условие, что при этом электрон не начнёт двигаться по циклоиде.
Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов 
не скомпенсирует магнитную составляющую силы Лоренца:
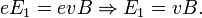
Скорость электронов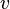 
можно выразить через плотность тока:
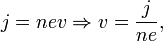
где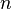 
— концентрация носителей заряда. Тогда
Коэффициент 
пропорциональности между и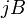 
называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определять их тип для большого числа металлов. Для некоторых металлов (например, таких, как свинец, цинк, железо, кобальт, вольфрам), в сильных полях наблюдается положительный знак 
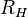, что объясняется в полуклассической и квантовой теориях твёрдого тела
65 Магни́тная инду́кция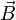 
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 
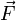магнитное поле действует на заряд 
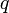, движущийся со скоростью 
.
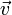Более конкретно, 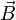— это такой вектор, что сила Лоренца 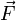, действующая со стороны магнитного поля[1] на заряд 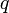, движущийся со скоростью 
, равна
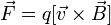
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора 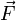перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)
1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
· результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
· Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.
· Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
· Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Был установлен экспериментально в 1820 году Био и Саваром и сформулирован в общем виде Лапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).
Закон Био—Савара—Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био—Савара—Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
В современной формулировке закон Био—Савара—Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля, т.е. в современной формулировке уравнения Максвелла выступают как более фундаментальные (прежде всего хотя бы потому, что формулу Био—Савара—Лапласа нельзя просто обобщить на общий случай полей, зависящих от времени).