Уравнения электростатики для диэлектриков

Давайте теперь свяжем полученные нами результаты с тем, что мы уже узнали в электростатике. Основное уравнение имеет вид

, (10.17)

где — плотность всех электрических зарядов. Поскольку уследить за поляризационными зарядами непросто, удобно разбить на две части. Обозначим снова через заряды, появляющиеся за счет неоднородной поляризации, а остальную часть назовем . Обычно означает заряд, сообщаемый проводникам или распределенный известным образом в пространстве. В этом случае уравнение (10.17) приобретает вид

или

. (10.18)

Уравнение для ротора от , конечно, не меняется:

. (10.19)

Подставляя из уравнения (10.8), получаем более простое уравнение:

Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.

В СИ: .

В СГС: .

Величина электрической индукции в системе СГС измеряется в СГСЭ или СГСМ единицах, а в Международной системе единиц (СИ) — в кулонах на м² (L⁻²TI). В рамках СТО векторы и объединяются в единый тензор, аналогичный тензору электромагнитного поля. Уравнения для вектора индукции в СГС имеют вид (2ая пара уравнений Максвелла)

Здесь — плотность свободных зарядов, а — плотность тока свободных зарядов. Введение вектора , таким образом, позволяет исключить из уравнений Максвелла неизвестные молекулярные токи и поляризационные заряды.

45. Исто́чник то́ка (также генератор тока) — двухполюсник, который создаёт ток, не зависящий от сопротивления нагрузки, к которой он присоединён. В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так. Более того, обычно используемые в быту источники электроэнергии по своим характеристикам гораздо ближе к источнику ЭДС, чем к источнику тока. Идеальный источник тока[править | править вики-текст]

Напряжение на клеммах идеального источника тока зависит только от сопротивления внешней цепи :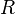

Мощность, отдаваемая источником тока в сеть, равна:

Поскольку для источника тока , напряжение и мощность, выделяемая им, неограниченно растут при росте сопротивления.

Реальный источник тока[править | править вики-текст]

Реальный источник тока в линейном приближении может быть описан при помощи внутреннего сопротивления . Реальный источник представляется как идеальный источник тока, соединенный параллельно со внутренним сопротивлением. Можно показать, что реальный источник тока с внутренним сопротивлением эквивалентен реальному источнику ЭДС, имеющему внутреннее сопротивление и ЭДС .

Напряжение на клеммах реального источника тока равно

Сила тока в цепи равна

Мощность, отдаваемая реальным источником тока в сеть, равна

Источником тока является катушка индуктивности, по которой шёл ток от внешнего источника, в течение некоторого времени ( ) после отключения источника. Этим объясняется искрение контактов при быстром отключении индуктивной нагрузки: стремление к сохранению тока при резком возрастании сопротивления (появление воздушного зазора) ведёт к пробою зазора.

Вторичная обмотка трансформатора тока, первичная обмотка которого последовательно включена в мощную линию переменного тока, может рассматриваться как почти идеальный источник переменного тока. Следовательно, размыкание вторичной цепи трансформатора тока недопустимо. Вместо этого при необходимости перекоммутации в цепи вторичной обмотки (без отключения линии) эту обмотку предварительно шунтируют.

Основные характеристики электрического тока:

а) сила тока I – численно равна количеству электричества (заряду) Q, протекающего по проводнику за время t:

I =

В зависимости от величины и направления токи бывают: постоянные, переменные, пульсирующие и другие. Будем рассматривать только постоянные токи I = const.

Ток измеряется прибором – амперметром, который включается в цепь последовательно проводнику (сопротивлению).

б) напряжение U – равно разности потенциалов на участке цепи.

Напряжение измеряется прибором – вольтметром, который включается параллельно проводнику (сопротивлению);

в) сопротивление R проводника.

лектродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых силнеэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура^[1].

По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил , под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре ЭДС будет равна:

где — элемент контура.

ЭДС так же, как и напряжение, в Международной системе единиц (СИ) измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого́ источника равна нулю.

Электри́ческое напряже́ние между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно отношению работы эффективного электрического поля (включающего сторонние поля^[1]), совершаемой при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда.

При этом считается, что перенос пробного заряда не изменяет распределения зарядов на источниках поля (по определению пробного заряда). Напряжение в общем случае формируется из двух вкладов: работы электрических сил и работы сторонних сил. В случае, когда на участке цепи не действуют сторонние силы (в этом случае ), работа по перемещению заряда складывается только из работы потенциального электрического поля , которая не зависит от пути, по которому перемещается заряд. В этом случае электрическое напряжение между двумя точками совпадает с разностью потенциалов между ними (поскольку ). В общем случае напряжение между двумя точками отличается от разницы потенциалов в этих точках^[2] на работу сторонних сил по перемещению единичного положительного заряда (эту работу называют электродвижущей силой на данном участке цепи, ):

46. Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде :

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

где:

· — ЭДС источника напряжения,

· — сила тока в цепи,

· — сопротивление всех внешних элементов цепи,

· — внутреннее сопротивление источника напряжения.

Закон Ома в дифференциальной форме[править | править вики-текст]

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

· — вектор плотности тока,

· — удельная проводимость,

· — вектор напряжённости электрического поля.

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид:

Удельная электропроводность – величина, обратная удельному сопротивлению.

=1/r (т.е.р) “хи” – “хаппа”

[ ] = Ом^-1·м^-1.

R=r·l/S , где: l – длина проводника (расстояние между

электродами).

S – площадь поперечного сечения (площадь электродов).

R – сопротивление раствора.

= l / (RS).

Удельная электропроводность – электропроводность раствора, помещённого между параллельными электродами, расположенными на расстоянии 1см площадью 1см².

Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении имитемпературы ниже определённого значения (критическая температура). Известны несколько сотен соединений, чистых элементов, сплавов икерамик, переходящих в сверхпроводящее состояние. Сверхпроводимость — квантовое явление. Оно характеризуется также эффектом Мейснера, заключающемся в полном вытеснении магнитного поля из объема сверхпроводника. Существование этого эффекта показывает, что сверхпроводимость не может быть описана просто как идеальная проводимость в классическом понимании.

Открытие в 1986—1993 гг. ряда высокотемпературных сверхпроводников (ВТСП) далеко отодвинуло температурную границу сверхпроводимости и позволило практически использовать сверхпроводящие материалы не только при температуре жидкого гелия (4.2 К), но и при температуре кипения жидкого азота (77 К), гораздо более дешевой криогенной жидкости.

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

В словесной формулировке звучит следующим образом^[2]

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Математически может быть выражен в следующей форме:

где — мощность выделения тепла в единице объёма, — плотность электрического тока, — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке исопротивления участка

В интегральной форме этот закон имеет вид

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени отt₁ до t₂.