Теорема кориолиса

Теорема о разложении абсолютного ускорения. Если точка движется в системе отсчета, которая в свою очередь движется относительно некоторой абсолютной системы отсчета, принимаемой за неподвижную, то абсолютное ускорение точки а_а является суммой трех ускорений: относительного ускорения a_r в движущейся системе отсчета; переносного ускорения а_t, т. е. ускорения той точки движущейся системы отсчета, с которой совпадает в данный момент движущаяся точка; дополнительного, так называемого поворотного ускорения, или ускорения Кориолиса а_c, обусловленного взаимным влиянием вращательного движения подвижной системы отсчета и относительного движения самой точки. При этом

где Ω — угловая скорость подвижной системы отсчета и V_r — относительная скорость рассматриваемой точки.

12 Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

где k — коэффициент жёсткости системы.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Энергия простого гармонического движения[править | править вики-текст]

Кинетическая энергия K системы в зависимости от времени t такова:

и потенциальная энергия есть

Полная механическая энергия системы, однако, имеет постоянное значение

Груз на пружине[править | править вики-текст]

Масса m, прикреплённая к пружине с постоянной жёсткостью k, является примером простого гармонического движения в пространстве. Формула

показывает, что период колебаний не зависит от амплитуды и ускорения свободного падения.

Универсальное движение по окружности[править | править вики-текст]

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерная проекция универсального движения по окружности. Если объект движется с постоянной угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x − y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник[править | править вики-текст]

Движениемаятника, не имеющего затуханий, можно приближённо рассматривать как простое гармоническое движение, если амплитуда колебаний очень мала в сравнении с длиной стержня.

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ с ускорением свободного падения g даётся формулой

Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от ускорения свободного падения g, поэтому при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускоренияпропорционально синусу координаты:

где

I — момент инерции; в данном случае I = m ℓ ².

Когда угол θ мал, можно считать, что sin θ ≈ θ, и выражение принимает вид:

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.

14 Давле́ние — физическая величина, численно равная силе F, действующей на единицу площади поверхности S перпендикулярно этой поверхности. В данной точке давление определяется как отношение нормальной составляющей силы , действующей на малый элемент поверхности, к его площади:

Среднее давление по всей поверхности есть отношение нормальной составляющей силы, действующей на данную поверхность, к её площади:

Давление характеризует состояние сплошной среды и является диагональной компонентой тензора напряжений. В простейшем случае изотропной равновесной неподвижной среды не зависит от ориентации. Является интенсивной физической величиной. Для обозначения давления обычно используется символ —- отлат. pressūra (давление).

Законом Паскаля в гидростатике называется следующее утверждение - давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.

Закон Архимеда формулируется следующим образом^[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме тела. Сила называется силой Архимеда:

где — плотность жидкости (газа), — ускорение свободного падения, а — объём погружённого тела

Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

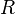где — давление газа в слое, расположенном на высоте , — давление на нулевом уровне ( ), — молярная масса газа, — универсальная газовая постоянная, — абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону:

где 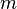— масса молекулы газа, — постоянная Больцмана.