Примеры нелинейных связей между переменными.
ЛАБОРАТОРНАЯ РАБОТА № 3
ПАРНОЕ НЕЛИНЕЙНОЕ УРАВНЕНИЕ РЕГРЕССИИ
Цель работы: рассчитать параметры показательного уравнения регрессии с помощью MS Excel; проанализировать качество построенной модели, используя индекс детерминации и среднюю ошибку аппроксимации; оценить статистическую значимость уравнения с помощью 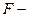 статистики.
статистики.
ТЕОРИЯ
Примеры нелинейных связей между переменными.
Связи между экономическими величинами необязательно выражаются линейными функциями – они могут быть и нелинейными. Так обратная зависимость спроса от цены может выражаться не только линейной функцией 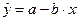 . Возможны и другие соотношения:
. Возможны и другие соотношения:  .
.
В демографических расчетах и страховом деле применяется функция вида 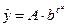 , которая называется уравнением Гомперца. Для описания развития производства новых товаров и роста численности населения используется логистическая функция (функция Ферхюльста)
, которая называется уравнением Гомперца. Для описания развития производства новых товаров и роста численности населения используется логистическая функция (функция Ферхюльста) 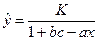 .
.
Различают два класса нелинейных регрессий:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам,
2) регрессии, нелинейные по оцениваемым параметрам. В свою очередь данный класс нелинейных уравнений делится на внутренне линейные и внутренне нелинейные.
Примерами нелинейной регрессии по включенным в нее объясняющим переменным являются следующие функции:
· полиномы разных степеней: 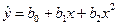 ,
, 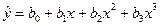 и др.
и др.
· равносторонняя гипербола: 
· уравнения с квадратными корнями, например,  , использовались в исследованиях урожайности, трудоемкости с/х производства
, использовались в исследованиях урожайности, трудоемкости с/х производства
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
· степенная  применяется при моделировании кривых спроса
применяется при моделировании кривых спроса
· показательная 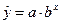 ;
;
· экспоненциальная  и др.
и др.
Уравнение Гомперца 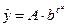 является примером нелинейности, как по включенным объясняющим переменным, так и по параметрам. Нелинейная регрессия первого класса не таит каких-либо сложностей в оценке ее параметров, то есть для поиска коэффициентов уравнения регрессии можно использовать МНК, предварительно устранив нелинейность методом замены переменной.
является примером нелинейности, как по включенным объясняющим переменным, так и по параметрам. Нелинейная регрессия первого класса не таит каких-либо сложностей в оценке ее параметров, то есть для поиска коэффициентов уравнения регрессии можно использовать МНК, предварительно устранив нелинейность методом замены переменной.
Рассмотрим данный прием на конкретных примерах.
Приведем к линейному виду – уравнение  . Пусть
. Пусть  , тогда получаем линейное уравнение регрессии
, тогда получаем линейное уравнение регрессии 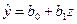 , параметры которого определяем из уже известной нам системы нормальных уравнений:
, параметры которого определяем из уже известной нам системы нормальных уравнений:

– аналогично приводятся к линейному виду уравнения  ,
,  и др.
и др.
Если нелинейная модель внутренне линейна, то с помощью соответствующих преобразований она может быть преобразована к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейному виду.
Нелинейность по параметру часто можно устранить путем предварительного логарифмирования и введения новых переменных и параметров.
Например, ищем уравнение регрессии вида  . Этапы преобразования к линейному виду:
. Этапы преобразования к линейному виду:
1) логарифмирование:  ;
;
2) введение новых переменных и параметров: 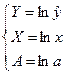 ;
;
Уравнение  приведено к линейному уравнению вида
приведено к линейному уравнению вида 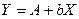 . Параметры уравнения регрессии находим из системы нормальных уравнений:
. Параметры уравнения регрессии находим из системы нормальных уравнений:

После нахождения параметра 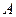 уравнения регрессии необходимо сделать обратную замену, то есть найти
уравнения регрессии необходимо сделать обратную замену, то есть найти 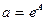 .
.