Примеры решения типовых заданий

Пример 5.1.По статистическим данным таблицы 5.1 для двенадцати транспортных компаний исследуется зависимость годового дохода (переменная , млн. руб.) от среднегодового количества грузовых автомобилей (переменная ).

1.Построить парную линейную модель зависимости от .

2. Проверить наличие в модели гетероскедастичности с помощью графического анализа и методом Голдфелда–Квандта.

3. При обнаружении гетероскедастичности построить взвешенную модель регрессии.

 

Таблица 5.1. Статистические данные примера 5.1

 

 

Решение:

1. По исходным данным строим линейную модель парной регрессии. Параметры ее оцениваем обычным методом наименьших квадратов. Коэффициенты уравнения регрессии определяем с помощью табличного процессора MS Excel: ; . Таким образом, уравнение регрессии имеет вид .

Уравнение регрессии статистически значимо на уровне a=0,05: наблюдаемое значение F‑статистики равно 25,15; критическое значение F-критерия Фишера – 4,96; коэффициент детерминации равен 0,716.

Значение коэффициента уравнения регрессии показывает, что увеличение количества автомобилей на одну единицу приводит к росту годового дохода в среднем на 4,277 млн. руб.

Визуальный анализ графика зависимости годового дохода от количества автомобилей дает основание предполагать наличие в модели гетероскедастичности. Из рисунка 5.5 видно, что отклонение от линии регрессии наблюдений, соответствующих крупным предприятиям, больше, чем для малых предприятий.

 

Рис. 5.5. График разброса точек наблюдений

относительно линии регрессии

 

2. Строим график остатков и проводим его визуальный анализ. В таблице 5.2 приведены наблюдаемые 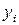и теоретические значения переменной , а также значения остатков .

 

Таблица 5.2. Наблюдаемые и теоретические значения переменной

 

 
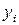
-8 -8 -31 -39 -55

 

График остатков представлен на рисунке 5.6.

 

Рис. 5.6. График остатков

 

Графический анализ остатков показывает, что их разброс растет по мере увеличения фактора , что может свидетельствовать о наличии гетероскедастичности. Проверим это предположение методом Голдфелда-Квандта. Будет считать, что остатки распределены по нормальному закону и их среднее квадратическое отклонение пропорционально значению фактора . Все остатки уже упорядочены по . Выбираем первых и последних остатков. Так как число наблюдений невелико, то оценим суммы квадратов остатков для крайних групп наблюдений по общей модели:

 

;

.

 

Так как , то наблюдаемое значение F-статистики рассчитываем по формуле .

Критическое значение F-критерия Фишера для уровня значимости a=0,05 и степеней свободы (где – число факторов в модели) составляет 19.

Так как , то статистическая гипотеза об одинаковой дисперсии остатков отклоняется на уровне значимости a=0,05. Факт наличия гетероскедастичности в модели считается установленным.

3. Применим взвешенный МНК к исходной модели в предположении, что среднее квадратическое отклонение остатков пропорционально значению фактора . Для этого масштабируем исходные данные по . Результаты масштабирования сведем в таблицу 5.3.

 

Таблица 5.3. Результаты масштабирования

 

 
0,0667 0,0556 0,0455 0,04 0,037 0,0323 0,0294 0,0270 0,0250 0,0222 0,0208 0,0208
15,67 13,89 11,23 10,4 10,63 8,45 9,03 7,57 8,93 9,11 8,10 6,48

 

Исходную модель преобразуем в модель . Оцениваем параметры преобразованной модели и обычным методом наименьших квадратов. С помощь MS Excel определяем коэффициенты уравнения регрессии , где , : ; . После этого уравнение принимает вид . Общее качество уравнения высокое: . Уравнение регрессии статистически значимо на уровне a=0,05: наблюдаемое значение F‑статистики равно 106 при критическом значении F-критерия Фишера 4,96.

Тест Голдфельда–Квандта, примененный к преобразованной модели , уже не выявляет гетероскедастичности ее остатков.

Используя преобразованное уравнение регрессии, делаем вывод, что увеличение количества автомобилей на одну единицу приводит к росту годового дохода в среднем на 3,863 млн. руб.

 

Пример 5.2.По статистическим данным за 12 месяцев, приведенным в таблице 5.4, исследуется зависимость цены акции предприятия (переменная , дол.) от индекса фондового рынка (переменная , пунктов).

1.Построить линейную парную регрессионную модель зависимости от фактора .

2. Проверить наличие автокорреляции остатков модели с помощью графического анализа и методом Дарбина-Уотсона.

3. При обнаружении автокорреляции построить обобщенную модель регрессии.

 

Таблица 5.4. Статистические данные примера 5.2

 

Месяц

 

Решение:

1. По статистическим данным строим модель парной регрессии, параметры которой оцениваем обычным методом наименьших квадратов. С помощью табличного процессора MS Excel определяем коэффициенты уравнения регрессии: ; . Уравнение регрессии имеет вид .

Уравнение регрессии статистически значимо на уровне a=0,05: коэффициент детерминации имеет значение ; ; .

Значение коэффициента уравнения показывает, что при росте индекса рынка на 1 пункт цена акции возрастает в среднем на 0,304 дол.

График зависимости от представлен на рисунке 5.7.

Рис. 5.7. График разброса точек наблюдений

относительно линии регрессии

2. Построим график временного ряда остатков регрессии (рисунок 5.8) и проведем его визуальный анализ. В таблице 5.5 приведены наблюдаемые 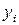и теоретические значения переменной , а также значения остатков .

 

Таблица 5.5. Наблюдаемые и теоретические значения переменной

 

Месяц
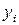
-3,9 4,8 6,2 -2,3 -8,1 -9,1 -7,6 -3,2 4,3 6,2 7,3 5,5

 

 

Рис. 5.8. График остатков

 

Визуальный анализ графика 5.8 указывает на положительную автокорреляцию остатков: видно, что на графике имеются чередующиеся зоны положительных и отрицательных остатков регрессии. Проверим это предположение методом Дарбина-Уотсона. Определяем -статистику по формуле

.

 

Критические значения -критерия для числа наблюдений и уровня значимости a=0,05 составляют и . Так как , то это свидетельствует о наличии положительной автокорреляции остатков.

3. Применим обобщенный метод наименьших квадратов для оценки параметров исходной модели, для чего преобразуем исходные данные по формулам , , .

Преобразованные данные представим в виде таблицы 5.6.

 

Таблица 5.6. Преобразованные данные

 

Месяц
- 65,7 58,8 57,3 95,9 110,3 97,2 91,0 53,7 85,0 119,5 123,6
- 56,7 50,4 40,6 51,9 59,0 57,2 58,7 52,1 58,7 69,1 67,8

 

Обычным методом наименьших квадратов определяем коэффициенты преобразованного уравнения регрессии : ; . Свободный член исходного уравнения теперь находим из равенства

 

.

 

Окончательно обобщенное уравнение линейной регрессии принимает вид .

Данное уравнение статистически значимо на уровне a=0,05: коэффициент детерминации имеет значение ; ; .

Таким образом, при росте индекса рынка на 1 пункт цена акции возрастает в среднем на 0,257 дол.

Пример 5.3.В таблице 5.7 приведены данные о заработной плате (доллары), возрасте (годы), стаже работы по специальности (годы), выработке (единицы за смену) для 20 рабочих предприятия.

1. Проверить наличие мультиколлинеарности между факторами.

2. Построить линейную регрессионную модель с полным набором факторов.

3. Определить факторы, ответственные за мультиколлинеарность.

4. Построить линейную регрессионную модель без факторов, ответственных за мультиколлинеарность.

5. Сравнить качество построенных моделей.

 

Таблица 5.7. Статистические данные примера 5.3

 

 

Решение:

1. С помощью табличного процессора MS Excel построим матрицу межфакторной корреляции:

 

.

 

Вычислим определитель этой матрицы: . Близость к нулю определителя матрицы межфакторной корреляции указывает на наличие сильной мультиколлинеарности факторов.

Статистическую значимость мультиколлинеарности определим проверкой нулевой гипотезы . Для проверки нулевой гипотезы используем распределение Пирсона с степенями свободы. Наблюдаемое значение статистики находится по формуле

 

,

где – число наблюдений, – число факторов. Для заданного уровня значимости по таблице критических точек распределения Пирсона определяется критическое значение . Так как , то гипотеза отклоняется и считается, что присутствует мультиколлинеарность факторов.

Построим матрицу парных коэффициентов корреляции:

 

.

 

Из матрицы видно, что между факторами (возраст) и (стаж по специальности) имеет место сильная линейная зависимость . Это также указывает на наличие мультиколлинеарности факторов.

2. С помощью табличного процессора MS Excel строим линейную регрессионную модель зависимости заработной платы от всех трех факторов. Она имеет вид . Проверка значимости коэффициентов регрессии при факторах в уравнении показывает, что статистически значимыми будут коэффициенты регрессии только при и . Поэтому полученное уравнение регрессии неприемлемо.

3. Из модели следует исключить фактор , так как он теснее связан с третьим фактором нежели фактор (это следует из анализа матрицы парных коэффициентов корреляции). Кроме того, фактор теснее связан с переменной . Отдавая предпочтение фактору , мы учитываем также, что в построенной трехфакторной модели коэффициент при не является статистически значимым.

4. Построим теперь уравнение линейной регрессии, исключив фактор . Это уравнение имеет вид .

5. В уравнении коэффициенты регрессии при переменных и значимы. Так как , то общее качество уравнения регрессии высокое. Новое уравнение значимо в целом, что подтверждается критерием Фишера.

 

Реализация с помощью ППП Excel

Расчет и анализ показателей множественной регрессии, а также проверка необходимых статистических гипотез могут быть осуществлены с помощью «Пакета анализа» табличного процессора Excel.

Методику применения ППП Excel проиллюстрируем на примере следующей задачи (при этом будем опираться на статистические данные, находящиеся в таблице 5.9, и исходить из того, что объем выборки равен 20).

Задача.Для объяснения заработной платы в зависимости от возраста и стажа по данной специальности построить и исследовать линейную регрессионную модель . Применить построенную регрессионную модель для прогноза заработной платы при .

Требуется:

1) ввести данные;

2) провести регрессионный анализ;

3) провести анализ общего качества уравнения регрессии;

4) указать стандартную ошибку регрессии;

5) указать стандартные ошибки коэффициентов регрессии;

6) проанализировать статистическую значимость коэффициентов при уровне значимости α = 0,05, при необходимости получить новое уравнение регрессии со значимыми коэффициентами;

7) найти точечные и интервальные оценки для коэффициентов регрессии;

8) дать точечный прогноз заработной платы по заданным значениям возраста и стажа;

9) рассчитать коэффициенты эластичности и сделать вывод о влиянии факторов на заработную плату.

Выяснить, выполняются ли условия теоремы Гаусса-Маркова для случайного члена:

1) проверить предположение о равенстве нулю математического ожидания случайного члена;

2) проверить предположение о наличии в модели гомоскедастичности остатков с помощью теста ранговой корреляции Спирмена, при необходимости построить взвешенную модель регрессии;

3) проверить предположение об отсутствии в модели автокорреляции остатков с помощью -статистики Дарбина-Уотсона, при необходимости построить обобщенную модель регрессии;

4) проверить гипотезу о нормальном распределении остатков;

5) сделать вывод о присутствии или отсутствии мультиколлинеарности факторов, при необходимости исключить один из факторов и построить парную линейную модель.

Результаты вычислений и анализа оформить в виде отчета (форма отчета прилагается ниже).

Порядок выполнения:

1) В ячейку А1 введите название Зарплата, в ячейку В1 – название Возраст, в ячейку C1 – название Стаж. В ячейки А2, А3, …, А21 введите данные первого столбца выбранного варианта задания, в ячейки В2, В3, …, В21 – данные второго столбца, в ячейки C2, C3, …, С21 – данные третьего столбца.

Введите новое название листа «Исходные данные», щелкнув правой кнопкой мыши на названии листа «Лист 1» и выбрав опцию переименование или двойным щелчком левой кнопкой мыши в поле «Лист 1».

2) Выберите в опциях меню Сервис → Анализ данных → Регрессия → ОК. Установите значения параметров в диалоговом окне следующим образом:

· Входной интервал Y — введите ссылки на ячейки A1:A21;

· Входной интервал X — введите ссылки на ячейки B1:C21;

· Метки — установите флажок;

· Уровень надежности — установите флажок;

· Константа ноль — оставьте пустым;

· Параметры вывода — установите флажок на Новый рабочий лист и в соответствующее поле введите его название «Регрессия»;

· Остатки — установите флажок;

· Стандартизированные остатки — оставьте пустым;

· График остатков — установите флажок;

· График подбора — установите флажок;

· График нормальной вероятности — оставьте пустым.

Нажмите ОК.

Расположите диаграммы рядом (на поле диаграммы нажмите левую кнопку мышки, затем поместите курсор на белое поле и при нажатой левой кнопке передвигайте диаграмму вниз) и растяните их (на поле диаграммы нажмите левую кнопку мышки, нижнюю линию границы диаграммы при нажатой левой клавише протяните вниз).

3) Значение коэффициента детерминации находится на листе «Регрессия» в ячейке В5. Наблюдаемое значение F-критерия Фишера находится на листе «Регрессия» в ячейке E12.

Вычислите критическое значение Fкр в свободной ячейке Е15 следующим образом:

– нажмите на fx (вставка функций);

– в поле Категория окна Мастер функций выберите статистические, из предложенных ниже функций выделите FРАСПОБР и нажмите ОК.

Откроется окно Аргументы функций. Заполните поля так:

· Вероятность — наберите значение 0,05;

· Степени свободы 1 — установите курсор в поле и выделите ячейку В12 столбца df таблицы «Дисперсионный анализ»;

· Степени свободы 2 — установите курсор в поле и выделите ячейку В13 столбца df таблицы «Дисперсионный анализ».

Нажмите ОК.

4) Значение стандартной ошибки 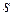регрессии находится на листе «Регрессия» в ячейке В7.

5) Значения стандартных ошибок коэффициентов регрессии находятся на листе «Регрессия» в ячейках С17, С18 и С19 соответственно.

6) Наблюдаемые значения -статистики коэффициентов регрессии , и находятся на листе «Регрессия» в ячейках D17, D18 и D19 соответственно.

Вычислите критическое значение в свободной ячейке D20 следующим образом:

– нажмите на fx (вставка функций);

– в поле «Категория» окна Мастер функций выберите статистические, из предложенных ниже функций выделите СТЬЮДРАСПОБР и нажмите ОК. Откроется окно Аргументы функций. Заполните поля:

· Вероятность – наберите значение 0,05;

· Степени свободы – введите 20-2-1, где 20 – число наблюдений, 2 – число факторов в уравнении регрессии, 1 – число свободных членов (a0) в уравнении регрессии.

Нажмите ОК.

7) Точечные оценки коэффициентов регрессии , и находятся на листе «Регрессия» в ячейках В17, В18 и В19 соответственно. Нижняя и верхняя границы доверительного интервала вычислены на листе «Регрессия» в ячейках F17 и G17 для коэффициента ,в ячейках F18 и G18 для коэффициента и в ячейках F19 и G19 для коэффициента .

8) На листе «Регрессия» в ячейке D22 введите формулу

= В17+В18*55+В19*25.

9) На листе «Исходные данные» введите формулы:

в ячейку А23 =СРЗНАЧ(А2:А21);

в ячейку В23 =СРЗНАЧ(В2:В21);

в ячейку С23 =СРЗНАЧ(C2:C21).

С листа «Регрессия» скопируйте ячейку В18 в ячейку В24 листа «Исходные данные», ячейку В19 – в ячейку С24 (значения коэффициентов регрессии).

В ячейку В25 введите формулу =В24*В23/А23 (для вычисления коэффициента эластичности переменной Возраст).

В ячейку С25 введите формулу =С24*С23/А23 (для вычисления коэффициента эластичности переменной Стаж).

Проверка модельных предположений:

1)Для проверки условия о равенстве нулю математического ожидания случайной величинына листе «Регрессия» выберите в опциях меню Сервис → Анализ данных → Описательная статистика → ОК. Установите значения параметров в диалоговом окне следующим образом:

· Входной интервал – введите ссылки на ячейки С25:С45 (столбец Остатки с названием);

· Группирование – установите флажок по столбцам;

· Метки – установите флажок в первой строке;

· Выходной диапазон – установите флажок на Новый рабочий лист и в поле напротив введите «Статистика»;

· Итоговая статистика – установите флажок;

· Уровень надежности (95%) – установите флажок.

Нажмите ОК.

Для оценки значимости среднего на листе «Статистика» в ячейку D3 введите формулу =(В3-0)*КОРЕНЬ(20)/В7 (для подсчета наблюдаемого значения статистики ). В ячейку D4 введите формулу =СТЬЮДРАСПОБР(0,05;20-1) (для подсчета критического значения распределения Стьюдента ).

2) Для проверки условия гомоскедастичности остатков с листа «Исходные данные» ячейки B1:B21 скопируйте в ячейку A1 нового листа, который назовите «Спирмен». В ячейку В1 скопируйте с листа «Регрессия» столбец «Остатки» вместе с названием. В ячейку С1 введите название «Модули». Выделите С2:С21 и введите формулу массива (нажмите F2, введите формулу, нажмите Ctrl+Shift+Enter) {=ABS(B2:B21)}.

Выберите в опциях меню Сервис → Анализ данных → Ранг и персентиль → ОК и заполните диалоговое окно следующим образом:

· Входной интервал – введите ссылки на ячейки A1:A21;

· Метки – установите флажок;

· Выходной интервал – ячейка D1.

Нажмите ОК.

Выберите в опциях меню Сервис → Анализ данных → Ранг и персентиль → ОК и заполните диалоговое окно следующим образом:

· Входной интервал – введите ссылки на ячейки С1:С21;

· Метки – установите флажок;

· Выходной интервал – ячейка Н1.

Нажмите ОК.

Выделите ячейки D2:G21 и нажмите кнопку Сортировка по возрастанию на панели инструментов. Выделите ячейки H2:K21 и нажмите кнопку Сортировка по возрастанию. Скопируйте ячейки F1:F21 в ячейку М1, ячейки J1:J21 в ячейку N1. Выделите ячейки О2:О21 и введите формулу массива {= (M2:M21-N2:N21)^2}.

Установите курсор на ячейке О22 и введите формулу

= 1-6*СУММ(О2:О21)/(20*(20^2-1)).

В ячейку О23 введите формулу = О22*КОРЕНЬ(19) (для вычисления )

В ячейку О24 введите формулу = СТЬЮДРАСПОБР(0,05;20-2) (для вычисления ).

 

3) Для проверки условия об отсутствии автокорреляции с листа «Регрессия» скопируйте столбец «Остатки» в ячейку А1 нового листа, который назовите «Автокорреляция».

В ячейки В2:В20 введите формулу массива {=(А2:А20-А3:А21)^2}.

В ячейку В22 введите формулу= СУММ(В2:В20).

В ячейки С2:С21 введите формулу массива {=(А2:А21)^2}.

В ячейку С22 введите формулу = СУММ(С2:С21).

В ячейку С23 введите формулу =В22/С22 (для вычисления DW).

4) Для проверки гипотезы о нормальном распределении остатков вернитесь на лист «Регрессия». Выберите в опциях меню Сервис → Анализ данных → Гистограмма → ОК. Заполните значения параметров окна следующим образом:

· Входной интервал – введите ссылки на ячейки С25:С45 (столбец Остатки листа «Регрессия» с названием);

· Интервал карманов – не заполняйте;

· Метки — установите флажок;

· Выходной диапазон – введите ссылку на Новый рабочий лист «Гистограмма»;

· Парето – оставьте пустым;

· Интегральный процент – оставьте пустым;

· Вывод графика – установите флажок.

Нажмите ОК. Перенесите гистограмму вниз и растяните ее.

5) Для проверки условия об отсутствии мультиколлинеарности откройте лист «Исходные данные», выберите в опциях меню Сервис → Анализ данных → Корреляция → ОК. Заполните значения параметров окна следующим образом:

· Входной интервал – ячейки В1:С21;

· Метки – установите флажок;

· Новый рабочий лист – «Мульти».

Нажмите ОК.

Скопируйте ячейку В3 в ячейку С2.

В ячейку А5 введите математическую формулу = МОПРЕД(B2:C3).

В ячейку А6 введите формулу =20-1-(1/6)*9*LOG(A5;10) (для нахождения хи-квадрат наблюдаемого).

В ячейку А7 введите формулу=ХИ2ОБР(0,05;1) (для нахождения хи-квадрат критического).

 

Приложение: Отчет о результатах вычислений и анализа

1. Постановочный этап

Из экономической теории известно, что заработная плата зависит от многих факторов, например, от ............... (перечислить основные факторы).

Выделим два фактора: Возраст и Стаж по специальности, которые являются объясняющими факторами для результативного (объясняемого) признака – Заработная плата. Возникает задача количественного описания зависимости указанных показателей уравнением множественной регрессии на основании статистических данных.

2. Спецификация модели

Предположим, что зависимость заработной платы от возраста и стажа по данной специальности описывается линейной регрессионной моделью , где – неизвестные параметры модели, 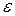– случайный член, который включает в себя суммарное влияние всех неучтенных в модели факторов.

3. Параметризация модели

Для оценки параметров уравнения множественной регрессии применяется метод наименьших квадратов (МНК). В результате проведения регрессионного анализа получены точечные и интервальные оценки неизвестных параметров.

Точечная оценка параметра равна ............... Интервальная оценка имеет вид ( ............, .............. ).

Точечная оценка параметра равна ................ Интервальная оценка имеет вид ( ............, ..............).

Точечная оценка параметра равна ............... Интервальная оценка имеет вид ( .............. , ............... ).

Таким образом, уравнение регрессии имеет вид (записать уравнение линейной регрессии).

4. Верификация модели

4.1. Значимость коэффициентов регрессии оценивается с помощью -статистики.

Для коэффициента наблюдаемое значение статистики tнабл равно ............... Критическое значение tкр равно ................ Так как |tнабл | (больше или меньше) tкр , то коэффициент (значим или незначим).

Для коэффициента регрессии наблюдаемое значение статистики tнабл равно ................ Критическое значение tкр равно ................ Так как |tнабл | (больше или меньше) tкр , то коэффициент (значим или незначим).

Для коэффициента регрессии наблюдаемое значение статистики tнабл равно ................ Критическое значение tкр равно ................ Так как |tнабл | (больше или меньше) tкр, то коэффициент (значим или незначим).

4.2. Качество построенной модели в целом оценивает коэффициент детерминации. В таблице «Регрессионная статистика» листа «Регрессия» коэффициент множественной детерминации R-квадрат равен .............. Сделать вывод об общем качестве уравнения.

Коэффициент множественной корреляции равен ................ Он оценивает тесноту совместного влияния факторов на результат. Сделать вывод о силе совместного влияния факторов.

Значимость коэффициента детерминации R-квадрат устанавливается с помощью критерия Фишера в таблице «Дисперсионный анализ» листа «Регрессия». Наблюдаемое значение Fнабл равно ............... Критическое значение Fкрравно ............... Так как наблюдаемое значение Fнабл (больше, меньше) Fкр , то R-квадрат (значим или незначим). Сделать вывод об общем качестве уравнения.

4.3. Для того, чтобы оценки параметров линейного уравнения множественной регрессии были несмещенными, состоятельными и эффективными, необходимо выполнение условий Гаусса–Маркова для случайного члена.

4.3.1. Значение «Среднее» из таблицы на листе «Статистика» равно ............... Оно является несмещенной оценкой математического ожидания случайного члена. Сделать вывод о выполнении предпосылки 1.

Значимость среднего устанавливается с помощью критерия Стьюдента. Так как |tнабл |=............... (больше или меньше) tкр =..............., то среднее (значимо или незначимо). Сделать вывод о выполнении предпосылки 1.

4.3.2. Для диагностики гетероскедастичности применяется тест ранговой корреляции Спирмена(лист «Спирмен»).Выдвигается нулевая гипотеза об отсутствии гетероскедастичности случайного члена. Так как |tнабл |=| ........... | (больше или меньше) tкр=................., то гипотеза об отсутствии гетероскедастичности (принимается или отвергается). Сделать вывод о выполнении предпосылки 2.

4.3.3. Для проверки гипотезы об отсутствии автокорреляции используется DW-статистика Дарбина-Уотсона. Критические значения DW-статистики находятся из таблицы 5.8.

 

Таблица 5.8. Значения DW-статистики при уровне значимости 0,05

(k – число факторов)

 

1,18 1,40 1,08 1,53 0,97 1,68 0,86 1,85
1,20 1,41 1,10 1,54 1,00 1,68 0,90 1,83
1,22 1,42 1,13 1,54 1,03 1,67 0,93 1,81

 

Так как DW = .............. при d1 = ........... и d2 = ............. попадает в зону (положительной автокорреляции, отрицательной автокорреляции, отсутствия автокорреляции, неопределенности), то автокорреляция (присутствует или отсутствует).

Сделать вывод о выполнении предпосылки 3.

4.3.4. Сделать вывод о нормальности распределения остатков по виду гистограммы. Дополнить графический анализ выводами на основе теста Жарка-Бера.

5. Для оценки мультиколлинеарности факторов используется определитель матрицы парных коэффициентов корреляции.Он равен ............ Анализ мультиколлинерности факторов осуществляется проверкой гипотезы на основании статистики Пирсона .

Наблюдаемое значение равно ............... Критическое значение равно ............... Так как наблюдаемое значение (больше, меньше) , то гипотеза (принимается или отвергается).

Сделать вывод о мультиколлинеарности факторов.

6. Частные коэффициенты эластичности для линейной регрессии рассчитывается по формуле: . Они равны ............... и ............. Сделать вывод о влиянии факторов по величине коэффициентов эластичности.

5. Прогнозирование

Если выполняются все условия верификации, то модель является качественной. В противном случае ее надо усовершенствовать: либо на этапе спецификации, либо варьировать выборку. По качественной модели можно прогнозировать объем заработной платы в зависимости от возраста и стажа по данной специальности. Сделать вывод о возможности прогнозирования.

Точечный прогноз экспорта равен ...................., доверительный интервал прогноза имеет вид (................, .................), где центр интервала равен точечному прогнозу, концы интервала получены прибавлением и вычитанием произведения стандартной ошибки прогноза на критическое значение t-статистики. Сделать вывод о качестве прогноза.