По графику и последним четырем значениям суммы видно то что ряд сходиться

 

Упражнение 2. Установить, расходимость каких из следующих рядов можно доказать, используя необходимый признак сходимости (по Вашему желанию: «вручную» или используя MATLAB):

а) ;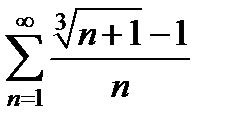

e=0.00001;

n=ceil(solve('abs (( (n+1)^(1/3)-1 ) / n ) = 0.00001'));

 

ni=n:0.1:n+10;

y=abs(((ni+1).^(1/3)-1)./ni);

ye=abs(((n+1)^(1/3)-1)/n);

plot(ni,y,ni,ye+e,'g-',ni,ye-e,'g-')

axis auto

Функция сходиться так как для любого епсилонт могу найти н по правилу сходимости

б) .

 

e=0.00001;

n=ceil(solve('abs(((n+3)/(n+1))^(2*n-1) )= 0.00001'));

 

ni=n:0.1:n+10;

y=abs(((ni+3)./(ni+1)).^(2*ni-1));

ye=abs(((n+3)/(n+1))^(2*n-1));

plot(ni,y,ni,ye+e,'g-',ni,ye-e,'g-')

axis auto

 

 

 

По графику видим что ряд не расходиться!

Упражнение 3.Приведите два примера расходящихся числовых рядов (отличные от рассмотренных в упр. 3), общий член которых стремится к нулю. Используя M-функцию из упр. 1, проиллюстрируйте примеры графически.

 

 

1) ;

 

clear

i=100000;

 

n=1:1:i;

f= 1./(n);

s(1)=f(1);

m=0.01;

for k=2:i;

s(k)=s(k-1)+f(k);

end

subplot(1,2,1);

plot (n,f,'m')

axis([i-10 i f(i-5)-m f(i-5)+m])

subplot(1,2,2);

plot (n,s,'g')

axis([i-100 i s(i-100)-m s(i-5)+m])

s(i-3)

s(i-2)

s(i-1)

s(i)