Расчет среднего значения и показателей вариации по несгруппированным данным
а. Примем данные ранжированного массива предприятий по размеру балансовой прибыли (табл. 2.4, столбец 4). На их основе рассчитаем средний размер прибыли по формуле средней арифметической простой, т.е. сложим все значения прибыли по совокупности предприятий и разделим на их количество - сорок:
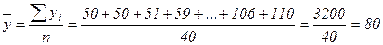 млн. руб.
млн. руб.
г. Показатели вариации:
- размах вариации:
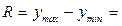 110 – 50 =60 млн. руб. –разница между крайними значениями размера прибыли в совокупности 40 предприятий оставляет 60 млн. руб.;
110 – 50 =60 млн. руб. –разница между крайними значениями размера прибыли в совокупности 40 предприятий оставляет 60 млн. руб.;
- среднее линейное отклонение определим по формуле:

Среднее линейное отклонение  показывает, что в среднем размер балансовой прибыли каждого из 40 предприятий отклоняется от среднего значения (80 млн. руб.) на 12,5 млн. руб. в большую и меньшую сторону;
показывает, что в среднем размер балансовой прибыли каждого из 40 предприятий отклоняется от среднего значения (80 млн. руб.) на 12,5 млн. руб. в большую и меньшую сторону;
- дисперсия признака на основании несгруппированных данных рассчитывается по формуле:
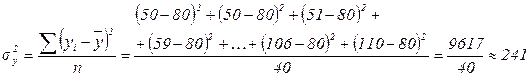 ;
;
- среднее квадратическое отклонение показывает, что в среднем размер прибыли каждого из 40 предприятий отклоняется от среднего значения (80 млн. руб.) на 15,5 млн. руб. в большую и меньшую сторону:
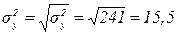 млн. руб.;
млн. руб.;
- коэффициент осцилляции свидетельствует о том, что размер отклонения крайних значений признака ( 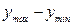 ) на 25% меньше среднего значения признака, что свидетельствует об умеренной вариации балансовой прибыли в выборочной совокупности 40 предприятий:
) на 25% меньше среднего значения признака, что свидетельствует об умеренной вариации балансовой прибыли в выборочной совокупности 40 предприятий:
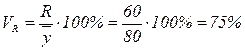 ;
;
- линейный коэффициент вариации для несгруппированных данных может рассчитываться только по среднему значению признака:
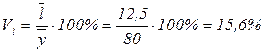 – размер отклонений индивидуальных значений размера балансовой прибыли предприятий от среднего значения, выраженный в процентах, составляет 15,6%;
– размер отклонений индивидуальных значений размера балансовой прибыли предприятий от среднего значения, выраженный в процентах, составляет 15,6%;
- коэффициент вариации признака равен:
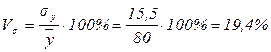 .
.
Поскольку коэффициент вариации ниже 20%, то можно судить об умеренной вариации размера прибыли в выборочной совокупности (т.е. совокупность достаточно однородна по изучаемому признаку).