Метод Гаусса (метод исключений)

Идея метода состоит в последовательном исключении неизвестных из системы n линейных уравнений.Метод Гауссасодержит два этапа: прямой ход, в процессе которого исходная система приводится к треугольному виду, и обратный ход – решение системы уравнений с треугольной матрицей.

Прямой ход.

На примере первого уравнения системы (1) рассмотрим выражение для x₁:

.

Подставим выражение для x₁ во второе и все остальные уравнения системы:

Для расширенной матрицы коэффициентов это означает, что каждый элемент первой строки следует поделить на диагональный элемент, а все остальные строки преобразовать, как показано выше. Таким образом, станут равны нулю все коэффициенты первого столбца, лежащие ниже главной диагонали. Затем аналогичная процедура проводится со второй строкой матрицы и нижележащими строками, при этом первая строка и первый столбец уже не изменяются. И так далее до тех пор, пока все коэффициенты, лежащие ниже главной диагонали, не будут равны нулю.

В результате приходим к эквивалентной системе с треугольной матрицей:

………. (2)

Общие формулы прямого хода:

k = 1…n, j = 1…n+1. Звездочкой отмечены элементы k-й строки с измененными значениями, которые будут подставлены в следующую формулу. Для определенности будем считать первый индекс – по строкам, второй – по столбцам.

 

i = k+1…n, j = 1…n+1, k фиксировано в уравнении (3). Для уменьшения количества действий достаточно изменять значения элементов, находящихся выше главной диагонали.

Умножим это уравнение последовательно на , и вычтем из третьего,...,n-го уравнения системы, получим

где элементы системы получены по формулам

, ( )

, ( , )

Продолжая этот процесс после n шагов получим преобразованную исходную систему

Таким образом, на -м шаге прямого хода коэффициенты , системы вычисляются по формулам

, ( , ) (1)

а коэффициенты , ( ) вычисляются по формулам

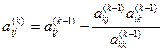, ( , ) (4)

причем

Обратный ход.

Второй этап решения СЛАУ методом Гаусса состоит в последовательном определении x_k, начиная с x_n, так как для последнего решение фактически получено.

Решение системы находят по рекуррентным формулам :

 

На обратном ходе вычисляют неизвестные в обратном порядке. Из последнего уравнения системы имеем , ,...,

Таким образом, вычисление неизвестных выполняется по формуле

( ) (3)

с известным .

 

2. Решение систем линейных уравнений методом итераций