Метод Гаусса (метод исключений)
Идея метода состоит в последовательном исключении неизвестных из системы n линейных уравнений.Метод Гауссасодержит два этапа: прямой ход, в процессе которого исходная система приводится к треугольному виду, и обратный ход – решение системы уравнений с треугольной матрицей.
Прямой ход.
Пусть требуется решить систему из n линейных алгебраических уравнений с n неизвестными переменными вида  ,
,
и пусть определитель ее основной матрицы отличен от нуля.
Будем считать, что  , так как мы всегда можем этого добиться перестановкой местами уравнений системы.
, так как мы всегда можем этого добиться перестановкой местами уравнений системы.
На первом шаге исключим неизвестную переменную x1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на  , к третьему уравнению прибавим первое, умноженное на
, к третьему уравнению прибавим первое, умноженное на  , и так далее, к n-ому уравнению прибавим первое, умноженное на
, и так далее, к n-ому уравнению прибавим первое, умноженное на  . Система уравнений после таких преобразований примет вид
. Система уравнений после таких преобразований примет вид

где
 ,
,  .
.
К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго.
На втором шаге с полученной системы, за исключением первого уравнения, действуем аналогично.

Будем считать, что  (в противном случае мы переставим местами вторую строку с k-ой, где
(в противном случае мы переставим местами вторую строку с k-ой, где  ). Приступаем к исключению неизвестной переменной x2 из всех уравнений, начиная с третьего.
). Приступаем к исключению неизвестной переменной x2 из всех уравнений, начиная с третьего.
Для этого к третьему уравнению системы прибавим второе, умноженное на  , к четвертому уравнению прибавим второе, умноженное на
, к четвертому уравнению прибавим второе, умноженное на 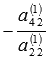 , и так далее, к n-ому уравнению прибавим второе, умноженное на
, и так далее, к n-ому уравнению прибавим второе, умноженное на 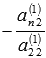 . Система уравнений после таких преобразований примет вид
. Система уравнений после таких преобразований примет вид

где  , а
, а  .
.
Таким образом, переменная x2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы

Так продолжаем прямой ход метода Гаусса пока система не примет вид

Таким образом, на  -м шаге прямого хода коэффициенты
-м шаге прямого хода коэффициенты  ,
,  (
(  ) системы вычисляются по формулам
) системы вычисляются по формулам
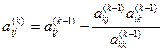 ,
,  (
(  ,
,  )
)
причем

 , а
, а  .
.
Обратный ход.
На обратном ходе вычисляют неизвестные в обратном порядке.
Из последнего уравнения полученной системы находим
 .
.
Далее с помощью полученного значения xn находим xn-1 из предпоследнего уравнения

И так далее, находим x1 из первого уравнения,...,
