Свойства МО

Св-во 1. Математическое ожидание по­стоянной величины равно самой постоянной:

М (С) = С.

Доказательство. Будем рассматривать постоян­ную С как дискретную случайную величину, которая имеет одно возможное значение С и принимает его с вероятностью р =1. Следовательно,

М(С) = С·1=С.

Две случ.величины Х и У назыв-ся независимыми, если з-н распределения одной из них не зависит от того, какие значения принимает другая величина.

Произведением двух СВ Х и У назыв-ся СВ ХУ, возможные значения к-рой = произведениям каждого из возможных значений одной на каждое возможное значение другой, а вер-ти возможных значений СВ ХУ = произведениям вер-тей возможных значений сомножителей.

Св-во 2. Математическое ожидание произведе­ния двух независимых случайных величин равно произведе­нию их математических ожиданий:

M(XУ) = M(X)M(У).

Док-во: приведем для СВ, имеющих по 2 возможных значения:

 

 

Тогда по опр-ю МО имеем: М(ХУ)= х1у1· рх1ру1+ х2у2· рх2ру2+х1у2·рх1ру2+х2у1· рх2ру1=х1рх1(ру1у1+ ру2у2)+х2рх2(ру1у1+ ру2у2)=(х1рх1+х2рх2)(ру1у1+ ру2у2)=М(Х)М(У). ЧТД

Замечание: Независимость СВ Х и У использовано при вынесении множителя ру1у1+ ру2у2 за скобки, т.к. это возможно при условии равенства выражений в обеих скобках, т.е. при одинаковом з-не распределения СВ У в случаях Х=х1 и Х=х2.

Следствие. Постоянный множитель можно выно­сить за знак математического ожидания:

М (СХ) = СМ (X).

Док-во: СВ Х и С независимы по смыслу. Поэтому М(СХ)=М(С)·М(Х), т.к. М(С)=С=>ЧТД

Замечание. Св-во 2 МО можно обобщить для нес-ких взаимно независимых СВ, например, для трех СВ: М(ХУZ)=М(Х)+М(У)+М(Z)

Суммой двух СВ Х и У назыв-ся СВ Х+У, возможные значения к-рой равны суммам каждого из возможных значений одной с каждым возможным значением другой, а вер-ти возможных значений СВ Х+У= произведениям вер-тей возможных значений слогаемых. Табл.распределения Х+У

 

 

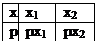
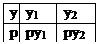
М(Х+У)= (х1+у1)(рх1ру1)+(х2+у2)(рх2ру2)+(х1+у2)(рх1ру2)+(х2+у1)(рх2ру1)=

=х1рх1(ру1+ру2)+х2рх2(ру1+ру2)+у1ру1(рх1+рх2)+у2ру2(рх1+рх2)=(х1рх1+х2рх2)+(у1ру1+у2ру2)=М(Х)+М(У)

Замечание. Св-во 3 можно обобщить для нескольких СВ: М(Х+У+Z)=М(Х)+М(У)+М(Z)

Пример 1. Реш-е: М(х)=2·0,3+4·0,6+5·0,1=3,5; М(у)=9,6; М(ХУ)=9,6*3,5=23,6

Пример 2. Реш-е: М(Х)=1/6(1+2+3+4+5+6)=7/2

СВ(У)-число выпавших очков на второй кости. Она идентична СВ(Х), т.е. Х=У, тогда: М(Х+У)=М(2Х)=2М(Х)=14/2=7