Векторы. Линейные операции над векторами. Базис. Координаты вектора.

 

Вектор-это направленный прямолинейный отрезок,т.е.отрезок,имеющий определённую длину и определённое направление.Если А-начало вектора,а В-его конец,то вектор обозначается символом Вектор (у него начало в точке В,а конец в точке А) называется противоположным вектору Вектор,противоположный вектору

Длиной и модулем вектора называется длина отрезка и обозначается Вектор,длина которого равна нулю,называется нулевым вектором и обозначается Нулевой вектор направления не имеет.

Вектор,длина которого равна единице,называется еденичным вектором и обозначается через

Под линейными операциями над векторами понимают операции

сложения и вычитания векторов, а также умножение вектора на

число.

Пусть 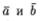-два ПРОИ3ВОЛЬНЫХ вектора. Возьмем произволь­

ную точку О и построим вектор 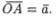От точки А отложим вектор Вектор соединяющий начало первого вектора с концом

второго, называется cуммой векторов

Это правило сложения векторов называют nравuло.м треУZО.ll'Ьншса.

Сумму ДВУХ векторов можно построить также по правилу nаралеллограмма (см . рис . 3).

 

 

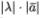Проuзведенuе вектора а на сколярное число называется вектором ,который имеет длину коллинеарен вектору имеет направление вектора ,если и противоположное

направление, если .

Из определения произведения вектора на число следуют свойства

этого произведения:

если Наоборот,если то при некотором верно равенство

всегда ,т.е.каждый вектор равен произведению его модуля на орт.

Линейные операции над векторами обладают следующими свой­

ствами:

Эти свойства позволяют проводить преобразования в линейных

операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скаЛярные, так и векторные общие множители.

 

(из википедии.в книжке не нашла)

Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:

Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).

Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,

В конечномерных пространствах обе разновидности базиса совпадают.