Гравитационное поле, моменты инерции Земли

Если бы Земля представляла собой точную сферу, в которой распределение плотности зависело бы только от радиуса, r=r(r), т.е. было бы сферически симметрично, то внешний гравитационный потенциал Земли имел бы исключительно простой вид (ньютоновский потенциал):

где r – расстояние от центра сферы, G – гравитационная постоянная, М – масса планеты. Гравитационный потенциал или гравитационная потенциальная энергия имеют тождественный смысл и математически описывают гравитационное поле. Реальная Земля близка к сфере. Она отклоняется от сферы на одну трехсотую. Поэтому основная часть внешнего гравитационного поля дается выражением (1). Отклонение внешнего гравитационного поля Земли от ньютоновского потенциала мало – порядка одной трехсотой и меньше, но оно содержит ценную информацию о небольших флуктуациях плотности в земных недрах, разностях моментов инерции Земли относительно ее главных осей и об отклонении земных недр от состояния гидростатического равновесия. До запусков ИСЗ за счет наземных измерений удалось определить первый поправочный член J₂ к ньютоновской части гравитационного поля (1). В результате внешнее гравитационное поле Земли по проведенным измерениям на ее поверхности представлялось формулой:

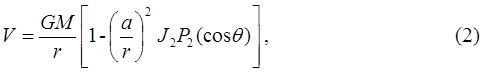
где a – экваториальная полуось,

Здесь

гравитационный момент, а

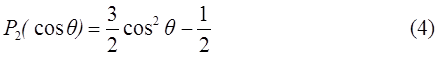
- второй полином Лежандра, С – момент инерции* относительно полярной оси, А – момент инерции относительно экваториальной оси, θ – полярный угол, равный дополнению широты до π/2, θ= π/2-φ. Современное J₂ равно 1082.65·10^-6. Таким образом, величина J₂, характеризующая отклонение гравитационного поля реальной Земли от сферически-симметричной части (1), как и должно быть, оказалось по величине порядка сжатия Земли, равного одной трехсотой. Соответственно, сжатие земного сфероида ε простым образом связано с J₂, угловой скоростью вращения ω, полной массой М и экваториальным радиусом a:

Если бы вся Земля была покрыта мировым океаном и поверхность его не возмущалась ветровыми волнами и приливами, то форма Земли совпадала бы с фигурой земного сфероида.

Для проблемы внутреннего строения Земли первостепенный интерес представляет величина среднего момента инерции

которая совместно со значением средней плотности

и данными сейсмологии позволяет определить распределение плотности в недрах Земли.

P.S. Величина I, равная сумме произведений элементарных масс на квадраты их расстояний от некоторой оси, называется моментом инерции тела относительно данной оси:

Суммирование производится по всем элементарным массам mi, на которые мысленно разбито тело.

Чтобы определить I, необходимо знать наряду с J₂ (3) еще какую-либо величину, так или иначе связанную с моментами инерции С и А. Из чисто гравиметрических измерений определить еще одно соотношение между моментами инерции С и А не удается. Но здесь на помощь гравиметрии приходит астрономия, методы которой позволяют определить постоянную прецессии земной оси

Распределение плотности в недрах планеты существенно влияет на средний момент инерции I (6) и, наоборот, значение I, определенное экспериментально, существенно контролирует распределение плотности при модельных расчетах. Рассмотрим случаи однородной модели – планеты с постоянным распределением плотности. Подсчитать момент инерции однородной сферы не составляет труда. В результате имеем

Отсюда следует, что в случае планеты постоянной плотности ее безразмерный момент инерции I* равен 0.4. Расчеты показывают, что при росте плотности в недрах планеты от периферии к центру величина I* будет принимать значение, меньшее 0.4. Наоборот, если в планете происходит уменьшение плотности с глубиной, то значение I* будет превосходить предельное значение, равное 0.4. Для Земли значение I* согласно наблюдениям равно 0.3315. Это соответствует существенной концентрации массы в центральных областях планеты. Таким образом, плотность Земли является возрастающей функцией глубины и ее возрастание происходит за счет сжатия под влиянием давления вышележащих слоев, за счет роста с глубиной концентрации тяжелой компоненты и иногда из-за уплотнения при фазовых переходах при высоких давлениях.

Внешним проявлением того факта, что в глобальном масштабе плотность увеличивается с глубиной или в случае малых тел остается почти постоянной, является условие I*≤ 0.4.

Исследование гравитационного поля Луны с помощью искусственных спутников Луны позволило определить ее безразмерный момент инерции

I*=0.392±0.003.

Этот фундаментальный результат указывает, что плотность Луны примерно постоянна.