ВОЛОКОННО-ОПТИЧЕСКИЕ ЛИНИИ СВЯЗИ

Для характеристики быстроты изменения скорости точки в механике вводится понятие ускорения.

Средним ускорением называется физическая величина, равная отношению изменения скорости материальной точки к длительности промежутка времени 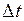, в течение которого это изменение произошло:

. (I.6)

 

Направление векторов и совпадают (рис.8).

 

Мгновенным ускорением (ускорением) материальной точки в момент времени называется физическая величина, равная пределу, к которому стремится среднее ускорение при бесконечном уменьшении промежутка времени :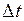

. (I.7)

 

Мгновенное ускорение является первой производной по времени скорости рассматриваемой точки, или второй производной по времени от радиус-вектора этой точки:

. (I.8)

 

Разложение ускорения точки по базису 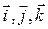, т.е. на три составляющие по осям прямоугольной декартовой системы координат:

, причем , ,

Если траектория точки – плоская кривая, то ускорение точки лежит в этой плоскости. В общем случае траектория точки – пространственная кривая, а ускорение лежит в соприкасающейся плоскости (см. Яворский и Детлаф «Курс физики»). В соприкасающейся плоскости есть два избранных направления – касательной к траектории (орт ) и главной нормали (орт ). Поэтому вектор удобно разложить на две составляющие вдоль этих направлений, т.е. по базису и (рис.9).

 

Рисунок 9

 

Вектор ускорения точки можно разложить на две составляющие: тангенциальную ( ) и нормальную ( )

Тангенциальная составляющая вектора ускорения направлена вдоль касательной к траектории в данной точке и называется тангенциальным (касательным) ускорением:

. (I.9)

Тангенциальное ускорение характеризует изменение вектора скорости по модулю. Вектор направлен в сторону движения точки при возрастании её скорости и в противоположную сторону – при убывании скорости.

Нормальная составляющая вектора ускорения, направлена по нормали к траектории к центру её кривизны в данной точке и называется нормальным (центростремительным) ускорением:

 

. (1.10)

Нормальное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении.

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.10):

 

. (I.11)

 

		Рисунок 10

 

 

В зависимости от тангенциальной и нормальной составляющих ускорения, движение будет подразделяться на несколько видов (таблица 1.):

 

Таблица 1. Классификация движения в зависимости от составляющих ускорения: тангенциального ( ) и нормального ( ).

N			Вид движения
			равномерное прямолинейное
	const		равнопеременное прямолинейное
	f(t)		прямолинейное движение с переменным ускорением
		const	равномерное движение по окружности
		0	равномерное криволинейное движение
	const	0	равнопеременное криволинейное движение
	f(t)	0	криволинейное движение с переменным ускорением

При криволинейном движении точки вектор ее ускорения всегда отклонен от касательной к траектории в сторону ее вогнутости. В случае ускоренного движения точки по криволинейной траектории угол между векторами и (рис.9) – острый. При замедленном – тупой.

!!! Дополнительно к лекции прочитать из моего пособия по основам механики §I.1.4 - §I.1.7 (буду спрашивать).

 

ВОЛОКОННО-ОПТИЧЕСКИЕ ЛИНИИ СВЯЗИ