Скорость. Ускорение

Кинематическое описание поступательного движения.

 

Положение материальной точки в пространстве в данный момент времени определяется по отношению к какому-либо другому телу, которое называется телом отсчета. С ним связывается система отсчета – совокупность системы координат и часов, связанных с телом, по отношению к которому изучается движение каких-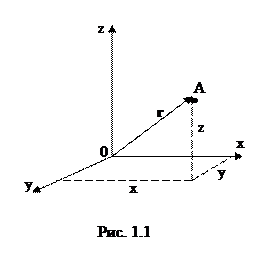нибудь других материальных точек. Выбор системы отсчета зависит от задач исследования. При кинематических исследованиях все системы отсчета равноправны (декартовая, полярная). В задачах динамики преимущественную роль играют инерциальные системы отсчета, по отношению к которым дифференциальные уравнения движения имеют более простой вид.

В декартовой системе координат положение точки А в данный момент времени по отношению к этой системе определяется тремя координатами х, у и z, или радиусом-вектором 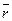(рис. 1.1). При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется уравнениями

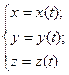(1.1)

или векторным уравнением

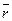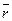=(t). (1.2)

Эти уравнения называются кинематическими уравнениями движения материальной точки.

Исключая время t в системе уравнений (1.1), получим уравнение траектории движения материальной точки. Например, если кинематические уравнения движения точки заданы в форме

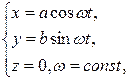
то, исключая t, получим:

 

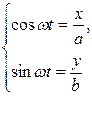, откуда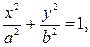

т.е. точка движется в плоскости z = 0 по эллиптической траектории с полуосями, равными a и b.

Траекторией движения материальной точки называется линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным и криволинейным.

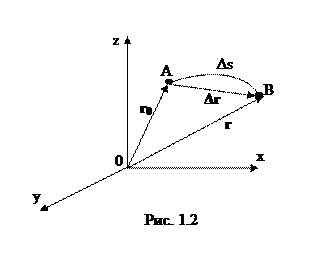Рассмотрим движение материальной точки вдоль произвольной траектории АВ (рис. 1.2). Отсчет времени начнем с момента, когда точка находилась в положении А (t = 0). Длина участка траектории АВ, пройденного материальной точкой с момента t = 0, называется длиной пути 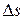и является скалярной функцией времени 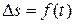. Вектор 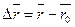, проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется вектором перемещения. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и его модуль 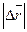равен пройденному пути .

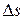Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени.

Пусть материальная точка движется по криволинейной траектории и в момент времени tей соответствует радиус-вектор 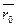. (рис. 1.3). В течение малого интервала времени 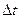точка пройдет путь 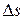и получит бесконечно малое перемещение 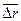. Различают среднюю и мгновенную скорости.

Вектором средней скорости 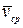называется отношение приращения 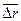радиуса-вектора точки к промежутку времени :

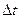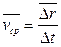(1.3)

Вектор 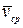направлен так же, как 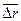. При неограниченном уменьшении 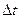, средняя скорость стремится к предельному значению, которое называется мгновенной скоростью или просто скоростью:

 

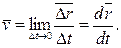(1.4)

 

Таким образом, скорость – это векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости 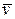направлен по касательной к траектории в сторону движения.

По мере уменьшения 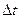длина 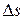дуги все более приближается к длине стягивающей ее хорды, т.е. численное значение скорости материальной точки равно первой производной длины ее пути по времени:

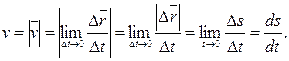
Таким образом,

(1.5)

Из выражения (1.5) получаем 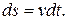Интегрируя по времени от 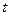до 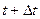, найдем длину пути, пройденного материальной точкой за время :

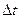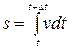(1.6)

Если направление вектора мгновенной скорости 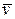во время движения материальной точки не изменяется, это означает, что точка движется по траектории, касательные к которой во всех точках имеют одно и то же направление. Таким свойством обладают только прямолинейные траектории. Значит, рассматриваемое движение будет прямолинейным.

Если направление вектора скорости 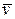материальной точки изменяется с течением времени, точка будет описывать криволинейную траекторию.

Если численное значение мгновенной скорости точки остается во время движения постоянным, то такое движение называется равномерным. В этом случае

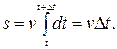(1.7)

Это означает, что за произвольные равные промежутки времени 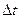материальная точка проходит пути равной длины.

Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее скорости с течением времени изменяется. Такое движение называется неравномерным. В этом случае пользуются скалярной величиной, называемой средней скоростью неравномерного движения на данном участке 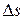траектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение пути 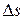затрачивается то же время 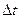, что и при заданном неравномерном движении:

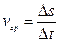(1.8)

Если материальная точка одновременно участвует в нескольких движениях, то по закону независимости движений ее результирующее перемещение равно векторной сумме перемещений, совершаемых ею за то же время в каждом из движений в отдельности. Поэтому скорость результирующего движения находится как векторная сумма скоростей всех тех движений, в которых материальная точка участвует.

В природе чаще всего наблюдаются движения, в которых скорость изменяется как по величине (модулю), так и по направлению, т.е. приходится иметь дело с неравномерными движениями. Для характеристики изменения скорости таких движений вводится понятие ускорения.

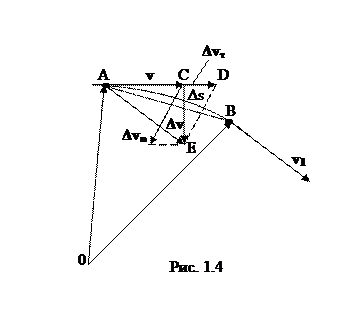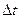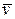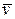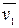Пусть за время движущаяся точка перешла из положения А в положение В (рис. 1.4). Вектор задает скорость точки в положении А. В положении В точка приобрела скорость, отличную от как по величине, так и по направлению и стала равной . Перенесем вектор в точку А и найдем .

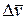Средним ускорением неравномерного движения в интервале времени от 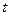до 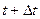называется векторная величина, равная отношению изменения скорости 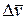к интервалу времени :

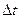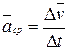(1.9)

Очевидно, что вектор 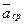совпадает по направлению с вектором изменения скорости .

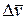Мгновенным ускорением или ускорением материальной точки в момент времени 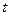будет предел среднего ускорения:

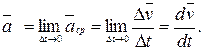(1.10)

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

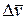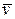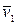Разложим вектор на две составляющие. Для этого из точки А по направлению скорости отложим вектор , по модулю равный . Тогда вектор 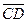, равный 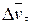, определяет изменение скорости по модулю (величине) за время 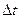, т.е. 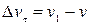. Вторая же составляющая вектора 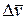характеризует изменение скорости на время 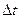по направлению - .

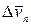Составляющая ускорения, определяющая изменение скорости по величине, называется тангенциальной составляющей 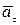. Численно она равна первой производной по времени от модуля скорости:

(1.11)

 

Найдем вторую составляющую ускорения, называемую нормальной составляющей. Допустим, что точка В достаточно близка к точке А, поэтому путь 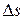можно считать дугой окружности некоторого радиуса r, мало отличающегося от хорды АВ. Из подобия треугольников АОВ и ЕАD следует, что

,

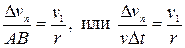
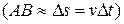откуда 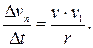В пределе при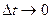 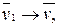поэтому вторая составляющая ускорения равна:

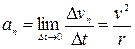. (1.12)

 

Она характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории по нормали. Ее называют также центростремительным ускорением.

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих:

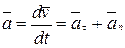. (1.13)

 

Из рис. 1.5 следует, что модуль полного ускорения равен:

(1.14)

Направление полного ускорения определяется углом 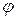между векторами и 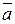. Очевидно, что

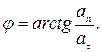(1.15)

В зависимости от значений тангенциальной и нормальной составляющих ускорения движение тела классифицируется по-разному. Если 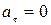(величина скорости не изменяется по величине), движение является равномерным. Если 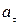> 0, движение называется ускоренным, если 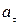< 0 – замедленным. Если 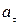= const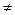0, то движение называется равнопеременным. Наконец, в любом прямолинейном движении 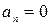(нет изменения направления скорости).

Таким образом, движение материальной точки может быть следующих видов:

1) 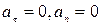- прямолинейное равномерное движение ();

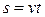2) 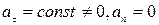- прямолинейное равнопеременное движение. При таком виде движения

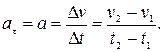
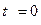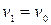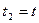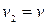Если начальный момент времени , а начальная скорость , то, обозначив и , получим:

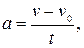
откуда 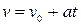. (1.16)

 

Проинтегрировав это выражение в пределах от нуля до произвольного момента времени, получим формулу для нахождения длины пути, пройденного точкой при равнопеременном движении:

 

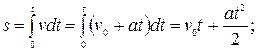(1.17)

 

3) - прямолинейное движение с переменным ускорением;

4) - скорость по модулю не изменяется, откуда видно, что радиус кривизны должен быть постоянным. Следовательно, данное движение по окружности является равномерным;

5) - равномерное криволинейное движение;

6) - криволинейное равнопеременное движение;

7) - криволинейное движение с переменным ускорением.

 

1.3. Кинематика вращательного движения твердого тела

 

Как уже отмечалось, вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси.

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси (рис. 1.6).Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка А движется по окружности радиуса R. Ее положение через промежуток времени 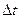зададим углом .

Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:

(1.18)

Единица измерения угловой скорости радиан в секунду (рад/с).

Таким образом, вектор определяет направление и быстроту вращения. Если , то вращение называется равномерным.

Угловая скорость может быть связана с линейной скоростью 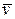произвольной точки А. Пусть за время 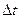точка проходит по дуге окружности длину пути 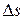. Тогда линейная скорость точки будет равна:

(1.19)

 

При равномерном вращении его можно охарактеризовать периодом вращения Т – временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π:

Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:

 

откуда

Для характеристики неравномерного вращения тела вводится понятие углового ускорения. Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

(1.20)

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора угловой скорости (рис. 1.7); при ускоренном движении вектор направлен в ту же сторону, что и , и в противоположную сторону при замедленном вращении .

Выразим тангенциальную и нормальную составляющие ускорения точки А вращающегося тела через угловую скорость и угловое ускорение:

 

(1.21)

 

(1.22)

 

 

В случае равнопеременного движения точки по окружности ():

,

где начальная угловая скорость.

Поступательное и вращательное движения твердого тела являются лишь простейшими типами его движения. В общем случае движение твердого тела может быть весьма сложным. Однако в теоретической механике доказывается, что любое сложное движение твердого тела можно представить как совокупность поступательного и вращательного движений.

Кинематические уравнения поступательного и вращательного движений сведены в табл. 1.1.

Таблица 1.1

Поступательное	Вращательное
Равномерное
Равнопеременное
Неравномерное

 

Краткие выводы

 

· Часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение, называется механикой. Классическая механика (механика Ньютона-Галилея) изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме.

· Кинематика – раздел механики, предметом изучения которого является движение тел без рассмотрения причин, которыми это движение обусловлено.

· В механике для описания движения тел в зависимости от условий конкретных задач используются различные физические модели: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело.

· Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение. Совокупность тела отсчета, связанной с ним системы координат и синхронизированных между собой часов называется системой отсчета.

· Вектор , проведенный из начального положения движущейся точки в положение ее в данный момент времени называется вектором перемещения. Линия, описываемая движущейся материальной точкой (телом) относительно выбранной системы отсчета называется траекторией движения. В зависимости от формы траектории различают прямолинейное и криволинейное движение. Длина участка траектории, пройденного материальной точкой за данный промежуток времени, называется длиной пути.

· Скорость – это векторная физическая величина, которая характеризует быстроту движения и его направление в данный момент времени. Мгновенная скорость определяется первой производной радиуса-вектора движущейся точки по времени:

Вектор мгновенной скорости направлен по касательной к траектории в сторону движения. Модуль мгновенной скорости материальной точки равен первой производной длины ее пути по времени:

· Ускорение – векторная физическая величина для характеристики неравномерного движения. Она определяет быстроту изменения скорости по модулю и направлению. Мгновенное ускорение - векторная величина, равная первой производной скорости по времени:

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по величине (направлена по касательной к траектории движения):

Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению (направлена к центру кривизны траектории):

Полное ускорение при криволинейном движении – геометрическая сумма тангенциальной и нормальной составляющих:

,

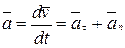· Векторная величина, определяемая первой производной угла поворота тела по времени, называется угловой скоростью:

Вектор направлен вдоль оси вращения по правилу правого винта.

· При равномерном вращении время, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π, называется периодом вращения:

Частота вращения – число полных оборотов, совершаемых телом при равномерном его движении по окружности в единицу времени:

· Угловое ускорение – это векторная физическая величина, определяемая первой производной угловой скорости по времени:

При ускоренном вращении тела вокруг неподвижной оси вектор сонаправлен вектору , при замедленном – противонаправлен ему.

· Связь между линейными (длина пути s, пройденного точкой по окружности радиуса R, линейная скорость v, тангенциальное ускорение , нормальное ускорение ) и угловыми характеристиками (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:

.

 

Вопросы для самоконтроля и повторения

 

1. Что является предметом изучения механики? Какова структура механики?

2. Что такое физическая модель? Какие физические модели использует механика для описания движения материальных объектов?

3. Что представляет собой система отсчета? Что называется вектором перемещения?

4. Какое движение называется поступательным? Вращательным?

5. Что характеризуют скорость и ускорение? Дайте определения средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения.

6. Составьте уравнение траектории движения тела, брошенного горизонтально со скоростью v₀ с некоторой высоты. Сопротивление воздуха не учитывать.

7. Что характеризуют тангенциальная и нормальная составляющие ускорения? Каковы их модули?

8. Как можно классифицировать движение в зависимости от тангенциальной и нормальной составляющих ускорения?

9. Что называется угловой скоростью и угловым ускорением? Как определяются их направления?

10. Какими формулами связаны между собой линейные и угловые характеристики движения?

 

Примеры решения задач

 

Задача 1. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета (рис. 1.8).