Машина Тьюринга

Машина Тьюринга есть математическая (вообразимая) машина, а не

машина физическая. Она есть такой же математический объект, как функция, производная, интеграл и т.д. А также, как и другие математические понятия, понятие машина Тьюринга отражает объективную реальность, моделирует некие реальные процессы.

Машина Тьюринга состоит из ленты, управляющего устройства и считывающей головки.

Лента разбита на ячейки. Во всякой ячейке в каждый момент времени находится в точности один символ из внешнего алфавита А={а₀,а₁,…а_n-1 }, n 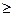2. Некоторый символ алфавита А называется пустым, любая ячейка, содержащая в данный момент пустой символ, называется пустой ячейкой.

В дальнейшем в качестве внешнего алфавита будем использовать А={0,1}, где в качестве пустого символа будем использовать 0 (нуль). В каждый момент времени лента содержит конечное число ячеек, но в процессе работы машины можно пристраивать новые ячейки в пустом состоянии.

Управляющее устройство в каждый момент времени находит в некотором состоянии q_i, принадлежащее множеству Q{q₀,q₁,…,q_r-1}, r 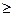1. Множество Q называется внутренним алфавитом. В дальнейшем начальное состояние будем обозначать символом q₁, а заключительное символом q₀ .

Считывающая головка перемещается вдоль ленты так, что в каждый момент времени она обозревает ровно одну ячейку ленты. Головка может считывать содержимое обозреваемой ячейки и записывать в нее вместо обозреваемого символа некоторый новый символ из внешнего алфавита.

Работа машины Тьюринга определяется программой. Программа состоит из команд. Каждая команда представляет собой выражение одного из следующего вида:

1) q_i a_j →q_k a_e;

2) q_i a_j →q_k a_e R;

3) q_i a_j →q_k a_e L.

Команда 1 заключается в том, что содержимое a_j обозреваемой на ленте ячейки стирается, а на его место дописывается символ a_e (который может совпадать с a_j ), машина переходит в новое состояние q_k (оно может совпадать с предыдущим состоянием q_i ).

Команда 2 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю справа ячейку.

Команда 3 работает аналогично команде 1, и дополнительно сдвигает считывающую головку в соседнюю слева ячейку.

Если считывающая головка находится в крайней справа (слева) ячейки ленты и происходит ее сдвиг вправо (влево), то к ленте пристраивается новая ячейка в пустом состоянии.

Машинным словом или конфигурацией называется слово вида

где А, q_k Q. Символ q_k пишется перед символом обозреваемой ячейки. Причем символ q_k может быть самым левым, но не может быть самым правым. В дальнейшем будем использовать следующее обозначение: а_iⁿ обозначает слово а_i а_i …а_{i =}

Например, конфигурация 1³q₁0²1² на ленте выглядит следующим образом: ▼q₁

 

 

Машина Тьюринга считается заданной, если заданы программа, внешний и внутренний алфавиты, и указано, какие из символов обозначают начальное и заключительное состояние.

Если машина Тьюринга выходит на заключительное состояние, то она называется остановившейся.

Пусть машина Тьюринга начинает работать в некоторый (начальный) момент времени. Слово, записанное в этот момент на ленте, называется начальным. Чтобы машина Тьюринга начала работать, необходимо поместить считывающую головку против какой-либо ячейки на ленте и указать,

в каком состоянии машина Тьюринга находится в данный момент.

Если Р – начальное слово, то машина Тьюринга, начав работу ”на слове” Р либо остановится через определенное число шагов, либо никогда не остановится. В первом случае говорят, что машина Тьюринга применима к слову Р и результатом применения машины к слову Р является слово М, соответствующее заключительной конфигурации.

Во втором случае говорят, что машина не применима к слову Р.

Пример 1 Выяснить, применима ли машина Тьюринга, задаваемая следующей программой

q₁0→ q₂0 R, q₁1→ q₁1 R, q₂0→ q₃0 R, q₂1→ q₁1 L, q₃0→ q₀0 , q₃1→ q₂1 R, к слову
Р= q₁ 1³0²1².

▼q₁

▼q₁

q₁1→ q₁1 R 1³ q₁0²1²

 

▼q₂

q₁0→ q₂0 R 1³0 q₂01²

 

▼q₃

q₂0→ q₃0 R 1³0² q₃1²

 

▼q₂

q₃1→ q₂1 R 1³0²1 q₂1

 

▼q₁

q₂1→ q₁1 L 1³0² q₁1²

 

▼q₁

q₁1→ q₁1 R 1³0²1² q₁0

 

▼q₂

q₁0→ q₂0 R 1³0²1² 0q₂0

 

▼q₃

q₂0→ q₃0 R 1³0²1² 0²q₃0

 

▼q₀

q₃0→ q₀0 1³0²1² 0²q₀0

 

Следовательно, данная машина Тьюринга применима к слову Р и заключительная конфигурация имеет вид: 1³0²1²0²q₀0.

В дальнейшем запись М M , будет означать, что машина Тьюринга (Т) через конечное число циклов перерабатывает машинное слово М в машинное слово М₁.

Функция называется вычислимой по Тьюрингу, если существует машина Тьюринга, вычисляющая её.

Во-первых, напомним, что речь идёт о частично-числовых функциях. Во-вторых, договоримся, что значения аргументов функции

f (х₁, х₂ … х_n) на ленте будут записываться следующим образом:

 

 

или .

Начинать переработку данного слова будем из стандартного положения, то есть из положения, при котором в состоянии q₁ обозревается крайняя правая единица описанного слова. Если функция f (х₁, х ₂ … х_n) определена на данном наборе значений аргументов, то в результате на ленте должно быть записано подряд f (х₁, х ₂ … х_n) единиц, в противном случае, машина должна работать бесконечно. При выполнении всех перечисленных условий, будем говорить, что машина Тьюринга вычисляет данную функцию f.

Пример 2 Построить машину Тьюринга, вычисляющую функцию

О(х) = 0. Для этого надо сконструировать машину Тьюринга (Т), (т.е. составить программу) которая начинает работу со слова q₁01 (х – любое натуральное число) останавливается, когда на ленте нет единиц

q₁01 => q 0

Данная программа имеет вид:

q₁0à q₂0R

q₂0 à q₀O

q₂1à q₂0R

Пример 3 Построить машину Тьюринга, вычисляющую функцию: f(x,y) = x + y. Построим машину Тьюринга (Т), которая, начиная работу со слова q₁01 01 останавливается когда на ленте х+у единиц q 01 01 =>q 01

q₁0 à q₂0R q2 0

q 0 à q OR q 0

q 1à q 1 q 0

q 1 à q 1R q 01

q 0 àq 1 q 1

q 1 à q 1L q 01

q 0 à q 0R q 1

q₅ 1à q 0 q 01

Пример 4 Построить машину Тьюринга, вычисляющую функцию

f(x) = 2/x. Эта функция не всюду определена. Лишь при х = 1, х = 2, её значениями являются натуральные числа 2 и 1 соответственно. Поэтому можно построить машину Тьюринга, которая начинает работу либо со слова q₁01, либо со слова q₁012останавливается, когда на ленте две единицы, одна единица соответственно. В остальных случаях машина начинает работу со слов q₂ (х ≠ 1, х ≠ 2) работает бесконечно. Такая машина задаётся следующей программой:

q 0 à q 0R q

q 0 à q 0

q 1 à q 1R 1 q 1

q 0 à q 1L q ,

q 1 à q 1R q 1

q 1 à q 1

q₄0 à q₅0L 1 q₅1

q₅1 à q₀0L q₀1,