Исследование переходных процессов в линейных электрических цепях постоянного тока.

 

Цель работы: исследовать характер переходных процессов в цепях, описываемых дифференциальными уравнениями первого порядка: по осциллограммам напряжений на элементах схемы определить постоянные времени исследуемых электрических цепей.

 

Согласно закону Ома в дифференциальной форме ток конденсатора равен:

,

и если U_C = const, то i_C = 0, т.е. в цепях постоянного тока конденсатор обладает бесконечно большим сопротивлением. Аналогично напряжение на индуктивности равно:

,

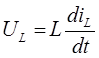и если i_L = const, то U_L = 0, т.е. в цепях постоянного тока индуктивность представляет собой короткое замыкание.

Конденсатор и индуктивность в цепях постоянного тока запасают энергию: конденсатор – электростатическую 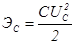, а индуктивность - электромагнитную 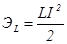. Процесс накопления энергии не может происходить мгновенно, поэтому при включении, выключении или изменении параметров цепи происходит изменение энергии, а поэтому ток конденсатора и напряжение на индуктивности не равны нулю, а изменяются по вполне определенному закону до тех пор, пока не будет запасена соответствующая энергия. Процессы, связанные с изменением энергии в конденсаторах и индуктивностях, называются переходными процессами и имеют место при любой коммутации цепи.

Из выражений для i_C и U_L следует, что напряжение на конденсаторе и ток в индуктивности не могут изменяться скачком (законы коммутации), т.е. значения этих величин до коммутации равны значениям после коммутации. Значения напряжений и токов в цепи до коммутации называют начальными условиями. Для того, чтобы получить закон изменения тока или напряжения на любом участке цепи во время переходных процессов, необходимо составить уравнения по закону Ома и Киргофа в дифференциальной форме и решить полученное дифференциальное уравнение. Частное решение дифференциального уравнения, т.е. решение уравнения с правой частью, дает установившиеся или принужденные значения напряжений и токов в цепи, т.е. значения напряжений и токов после окончания переходных процессов. Общее решение дифференциального уравнения (с нулевой правой частью) дает свободные составляющие напряжений и токов в цепи, характеризующих переходный процесс в цепи. Полные значения напряжений и токов в цепи находятся как сумма принужденной и свободной составляющих:

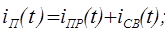
Закон изменения свободных составляющих во времени одинаков для всех напряжений и токов данной цепи. Для схемы рис.7.1а можно составить уравнение по законам Ома и Киргофа:

После дифференцирования получим:

Так как правая часть полученного уравнения равно нулю, то принужденное значение тока в цепи равно нулю:

I_пр = 0.

Для нахождения общего решения дифференциального уравнения запишем характеристическое уравнение и найдем его корни:

Для уравнений первого порядка решение находится в виде:

где А - постоянная интегрирования, находится исходя из начальных условий. Если U_C(0) = 0, то при включении схемы , с другой стороны:

i_п(t) = i_пр + i_св(t) = 0 + ;

i_п(0) = A; .

Следовательно:

i_п(t) = i_св(t)=

Аналогично для схемы рис.7.1б получим:

Для нахождения принужденной составляющей тока полагаем и

Характеристическое уравнение цепи и его корень:

R + pL = 0;

Следовательно:

.

В цепях, описываемых дифференциальными уравнениями первого порядка, напряжения и токи в цепи описываются экспонентами вида или . Построение таких функций удобно производить в масштабе времени, кратном (рис.7.2).

 

t
	0.37	0.63
2	0.135	0.865
3	0.05	0.95
4	0.018	0.982
5	0.007	0.993

 

Спустя время t = 5τ свободная составляющая уменьшается до величины менее 1% от начального значения. Поэтому принято считать, что переходной процесс в цепи длится не более 5τ.