Исследование линейных электрических цепей переменного тока.

Цель работы: экспериментально проверить выполнение законов Ома и Киргофа для цепей переменного тока, определить фазовые соотношения между напряжениями и токами в схеме.

В цепях переменного синусоидального тока кроме активных сопротивлений (резисторов) используются реактивные элементы: конденсаторы и индуктивности. В соответствии с законом Ома в дифференциальной форме для активного сопротивления R, индуктивности L и конденсатора С можно получить выражение для тока и напряжения на каждом виде элементов в цепях переменного тока

( i = I_msinωt):

для активного сопротивления R:

для индуктивности L:

для конденсатора С:

или если U_C = U_m sinωt, то

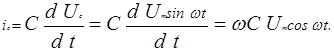
Отсюда следует, что в активном сопротивлении ток и напряжение совпадают по фазе, в индуктивности напряжение опережает ток на , в конденсаторе напряжение отстает от тока на .

При последовательном соединении R,L и С, когда через элементы цепи протекает один и тот же ток, падение напряжения на элементах цепи будут ориентированы относительно тока в соответствии с указанным выше, и поэтому второй закон Киргофа для цепей переменного тока рассматривается в векторной форме. При параллельном соединении R,L и C общей величиной для всех элементов является напряжение, а токи в ветвях будут ориентироваться относительно напряжения, поэтому первый закон Киргофа также выполняется в векторной форме.

В смешанных RC и RL цепях ток и напряжение сдвинуты друг относительно друга на угол меньше ,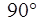

или .

Для удобства определения фазовых соотношений в электрических цепях переменного тока используют комплексный метод расчета цепей, в котором положение векторов напряжения и тока представляется на комплексной плоскости. Для реализации полученных фазовых соотношений между напряжением и током на элементах схемы сопротивления последних выражают в комплексной форме:

(Умножение величины на j равносильно повороту вектора на + , на -j –на - ).

При использовании выражений для сопротивлений в комплексной форме для цепей переменного тока справедливы все методы расчета цепей постоянного тока. Отличие заключается лишь в том, что расчеты ведутся в комплексной форме, и каждый ток или напряжение на участке цепи выражается комплексным числом вида:

Обычно при расчетах цепей переменного тока одну величину (чаще всего напряжение источника питания цепи) направляют по действительной оси, т.е. начальная фаза этой величины принимается равной нулю, а все остальные полученные в ходе расчета величины будут иметь определенные фазы, т.е. характеризоваться определенным положением вектора на комплексной плоскости. Для каждой цепи переменного синусоидального тока можно построить векторную диаграмму, по которой можно судить о фазовых соотношениях между любыми соотношениями электрической цепи.