Определение 13

1. Каждая нульместная предикатная переменная есть формула.

2. Если А(…) – n-местная предикатная переменная, то А(х1,х2,…,хn) есть формула, в которой все предикатные переменные х1,х2,…,хn свободны.

3. Если F – формула, то – также формула. Свободные (связанные) предметные переменные в формуле те и только те, которые являются свободными (связанными в F).

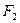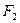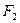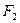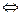
4. Если и – формулы, и предметные переменные, входящие одновременно в обе эти формулы, свободны в каждой из них, то выражения , Ú , , 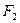также являются формулами.

5. Если F – формула и х – предметная переменная, входящие в F свободны, то выражения 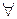хF и 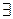хF также являются формулами, в которых переменная х связанная и все остальные предметные переменные, входящие в формулу F свободно или связанно остаются и в новых формулах соответственно такими же.

6. Других формул логики предикатов, кроме получающихся согласно пунктам 1–5, нет.

Например, А(х,y) B(z) – элементарные формулы, и

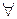х А(х,у), ( 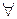хВ(х)) 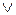; 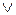( 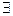х А(х,у)), 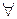х А(х,у) В(у) – составные формулы.

Формулы, в которых все переменные связаны, называются замкнутыми, а формулы, содержащие свободные предметные переменные, – открытыми.

Примерами замкнутых формул являются

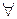х 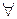у А(х,у), 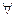х В(х) 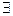у А(у).

Если в формулу алгебры логики вместо каждой предикатной переменной подставить конкретный предикат, определенный на множестве М, то формула превращается в конкретный предикат, определенный на М. Причем, если формула замкнута, то после такой подстановки мы получаем высказывание. Если в исходной формуле были свободные переменные, то после такой подстановки мы получаем конкретный предикат от таких переменных. Если теперь вместо таких переменных подставить их конкретное значение, то мы опять получим высказывание.

Такое превращение формулы алгебры логики в высказывание называется интерпретацией этой формулы на множестве М.

Рассмотрим формулу 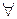х А(х,у) 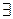х А(х,у). В качестве М возьмем множество всех действительных чисел. В данную формулу вместо предикатной переменной А(х,у) подставим конкретный предикат х + у > 2 определенный на R. Получаем 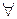х(х+у > 2) 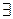х(х+у > 2) предикат, зависящий от переменной у. Вместо у подставим любое конкретное значение у0 из F.

Получаем высказывание 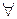х(х+у0 > 2) 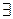х(х+у0 > 2), так как

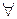х(х+у0 > 2)=0, 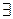х(х+у0 > 2)=1.

Ясно, что предикат 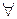х(х+у >2) 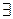х(х+у0 > 2) – тождественно истинный предикат.

Определение 14 Формула алгебры логики предикатов называется выполнимой на множестве М, если при некоторой подстановке вместо предикатных переменных конкретных предикатов, определенных на этом множестве, она превращается в выполнимый предикат. Другими словами, формула выполнима на М, если существует истинная ее интерпретация на М.

Например, формула 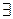хА(х) В(у) выполнима на множестве R. Действительно, подставляя в данную формулу вместо предикатных переменных конкретные предикаты (х > 2),(у < 3), получаем предикат 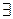х(х >2) (у <3) зависящий от у. Данный предикат выполнимый. Действительно, пусть у=2. Ясно, что высказывание 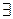х(х > 2) (2 < 3) истинно.

Определение 15 Формула алгебры логики предикатов называется тождественно истинной (тождественно ложной) на множестве М, если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на этом множестве, она превращается в тождественно истинный (тождественно ложный) предикат.

Определение 16 Формула алгебры логики предикатов называется тавтологией (противоречием), если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах, она превращается в тождественно истинный (тождественно ложный) предикат.

Покажем, что формула 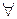хА(х) 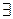хА(х) является тавтологией. Пусть А(х) – любой конкретный предикат, определенный на любом множестве М. Покажем, что после такой подстановки в формулу мы получаем истинное высказывание.

Предположим противное 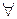хА(х) 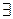хА(х)=0. Тогда 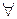хА(х)=1 и 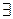хА(х)=0.

Отсюда следует, что А(х)≡ 1 и А(х)≡ 0 одновременно, что невозможно.

Покажем, что формула 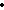( 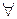уА(у)) является противоречием. Предположим, что это не так. Тогда найдется конкретный предикат А(х), определенный на конкретном множестве М, после подстановки которого в исходную формулу мы получаем выполнимый предикат на множестве М. А это значит, что найти значение a из М, что ( 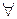уА(у))=1. Но тогда =1 и 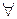уА(у)=1. Отсюда следует, что А(а)=0 и A(y) – тождественно истинный предикат на М, одновременно. Получили противоречие.

Нахождение тавтологий является одной из важнейших задач логики предикатов. В алгебре высказываний существует алгоритм, позволяющий выяснить, является ли формула алгебры высказываний тождественно истинной или нет. Для этого нужно составить таблицу истинности формулы. Если последний столбец состоит только из единиц, то формула тождественно истинна. Аналогичная проблема о существовании такого алгоритма возникает и для формул алгебры логики предикатов. В 1936 году американским математиком А. Чёрчем было доказано, что такого алгоритма не существует. Каждая форма подлежит изучению индивидуальным методом на тождественную истинность. Тем не менее, для некоторых частных видов формул данная проблема допускает решение, в частности, для формул алгебры логики предикатов, определённых на конечных множествах.

Действительно, пусть формула алгебры логики предикатов задана на конечном множестве. Тогда вместо её предикатных переменных могут подставляться конкретные предикаты, определённые на этом множестве. Согласно теоремам 6 и 7 операции квантификации на конечном множестве сводятся к конъюнкции и дизъюнкции. Следовательно, задача о том является ли формула тавтологией, сводится к аналогичной задаче для алгебры высказываний, которая эффективно разрешима.