Кванторные операции над предикатами
Операции отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность определяются аналогично как для предикатов, так и для высказываний. Однако в теории предикатов существуют операции, для которых нет аналогов в теории высказываний. Такими операциями над предикатами являются две кванторные операции – квантор общности и квантор существования. Известно, что если в одноместном предикате зафиксировать значение переменной, то мы получим высказывание.
Имеется еще один способ. Он основан на применении к предикату операций связывания квантором общности или квантором существования. Такие операции ставят в соответствие одноместному предикату высказывание, значение которого зависит от строения исходного предиката.
Определение 11Пусть A(x) – одноместный предикат, определенный на множестве M. Обозначим через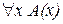 
высказывание, которое читается: «для всякого x из M справедливо A(x)», данное высказывание истинно только в том случае, когда предикат A(x) тождественно истинный.
Символ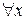 
называется квантором общности по переменной x.
Например, пусть A(x)=(x2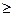 
0) одноместный предикат, определенный на множестве R. Тогда 
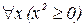– истинное высказывание, которое читается: «квадрат любого действительно числа неотрицателен». Пусть
A(x)=(x > 2). Тогда 
– ложное высказывание, которое читается: «любое действительное число больше 2».
Следующая теорема показывает, что квантор общности можно рассматривать как обобщение конъюнкции.
Теорема 6Пусть A(x) – одноместный предикат, определенный на конечном множестве M={ a1,a2, … ,an}, тогда 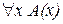= A(a1)·A(a2)·…·A(an).
Доказательство.Пусть 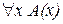= 1, тогда A(x)≡1. Отсюда A(ai)=1 для любого aiÎM. Но тогда A(a1)·A(a2)·…·A(an)=1. Пусть 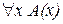= 0, тогда
A(x)¹1. А это значит, что существует ai из M, что A(ai)=0. Но тогда A(a1)·A(a2)·…·A(an)=0. Теорема доказана.
Квантор общности можно применять и к многоместным предикатам. Однократное применение квантора к одной из n переменных n-местного предиката порождает (n-1) – местный предикат.
Пусть, например, мы имеем двухместный предикат A(x,y)=(x > y), определенный на множестве R. Тогда "x (x > y) задает одноместный предикат B(y), зависящий от переменной y. Определим тип этого предиката. Возьмем произвольное действительное число y0. Ясно, что
B(y0)= "x(x > y0)=0. Следовательно, B(y) – тождественно ложный предикат.
Заметим, что к (n-1)-местному предикату "x1 A(x1,x2, … ,xn), зависящему от переменных х1, x2,x3, … ,xn, можно снова применять операцию связывания квантором общности по одной из свободных переменных. В результате получится (n-2)-местный предикат и т.д.
Пусть, например, мы имеем двухместный предикат A(x,y)=(x+y > 2), определенный на R. Тогда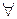 
x"y (x+y > 2) – ложное высказывание, которое читается: «сумма любых двух действительных чисел больше двух».
Определение 12Пусть A(x) – одноместный предикат, определенный на множестве M. Обозначим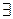 
x A(x) – высказывание, которое читается: «существует x из M, что справедливо A(x)», данное высказывание ложно только в том случае, когда предикат A(x) тождественно ложный.
Символ 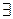x называют квантором существования по переменной x.
Например, пусть предикат A(x)=(x2<0) определен на R. Тогда 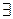x (x2<0) – ложное высказывание, которое читается: «существует действительное число, квадрат которого меньше 0».
Следующая теорема показывает, что квантор существования можно рассматривать как обобщение дизъюнкции.
Теорема 7Пусть A(x) – одноместный предикат, определенный на конечном множестве M={a1,a2, … ,an}. Тогда 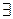x A(x)=A(a1)VA(a2) V…VA(an).
Доказательство. Пусть 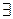x A(x)=0. Тогда согласно определению 12 A(x) – тождественно ложный предикат, а значит A(ai)=0 для любого aiÎM, но тогда A(a1)VA(a2) V…VA(an)=0. Пусть 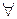x A(x)=1.Тогда А(х) – не тождественно ложный предикат. А это значит, что найдется значение аiиз М,что А(аi)=1.Но тогда А(а1)V А(а2)V…VА(аn)=1.Теорема доказана.
Квантор существования можно применять к многомерным предикатам. Однократное применение квантора к одной из n переменных а-мерного предиката порождает (n-1)-мерный предикат.
Пусть, например, мы имеем двухместный предикат А(х,у)=(х > у) определённый на множестве R. Тогда 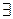х(х > y) задает одноместный предикат В(у), зависящий от переменной у. Данный предикат будет тождественно истинным. Действительно, пусть у0 – произвольное фиксированное действительное число. Тогда В(у0)= 
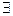х(х > y0)=1.
Заметим, что если в многомерном предикате все переменные связаны кванторами, то он будет высказыванием.
Пусть А(х,у)=(х+у > 1) двухместный предикат определённый на множестве R.
Тогда из него связыванием переменных х и у можно получить восемь высказываний:
1 "х"у(х + у > 2) – “Для всяких действительных чисел х и у их сумма больше двух”.
2 "у"х(х + у > 2) – “Для всяких действительных чисел у и х их сумма больше двух”.
3 $х$у(х + у > 2) – “Существуют действительные числа х и у, сумма которых больше двух”.
4 $у$х(х + у > 2) – “Существуют действительные числа у и х, сумма которых больше двух”.
5 "х$у(х + у > 2) – “Для всякого действительного числа х существует действительное число у, что их сумма больше двух”.
6 "у$х(х + у > 2) – “Для всякого действительного числа у существует
действительное число х, что их сумма больше двух”.
7 $х"у (х+у>2) – “Существует действительное число х, что для всякого действительного числа у их сумма больше двух ”.
8 х (х+у>2) – “Существует действительное число у, что для всякого
действительного числа х их сумма больше двух ”.
Нужно заметить, что высказывания 1 и 2 оба ложны и имеют один и тот же смысл; высказывания 3 и 4 оба истинны и имеют один и тот же смысл. Как видно, изменение порядка одноименных кванторов не влияет на смысл и значение истинности высказывания. Высказывание 5 истинно, а высказывание 8 ложно.
Высказывание 7 ложно, а высказывание 6 истинно. Как видно, изменение порядков разноименных кванторов приводит к изменению смысла и, возможно, значения истинности высказывания.