Сокращенная и тупиковая ДНФ.
В теме 3 было показано, что любая булева функция может быть представлена дизъюнктивной нормальной формой. Следует отметить, что дизъюнктивная нормальная форма часто допускает упрощение. При этом путем различных тождественных преобразований получится дизъюнктивная нормальная форма, эквивалентная исходной, но содержащая меньшее число вхождений символов.
Дизъюнктивная нормальная форма называется минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей дизъюнктивными нормальными формами.
Заметим, что если некоторый символ в формуле, скажем  , встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
, встречается, например, два раза, то при подсчете числа символов в формуле он учитывается два раза.
Основной вопрос данного параграфа – как для произвольной булевой функции построить ей минимальную дизъюнктивную нормальную форму. Эта задача называется проблемой минимизации булевых функций.
Существует тривиальный алгоритм построения минимальной ДНФ для произвольной булевой функции  . Для этого все ДНФ, составленные из символов
. Для этого все ДНФ, составленные из символов  упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение
упорядочиваются по числу букв и по порядку для каждой ДНФ Д проверяется соотношение  . Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции
. Первая по порядку ДНФ, для которой это соотношение выполняется, есть, очевидно, минимальная ДНФ функции  .
.
Число различных ДНФ, составленных из переменных  , равно
, равно  .
.
Прежде чем доказать данное утверждение, приведем следующее определение.
Конъюнкция  называется элементарной, если
называется элементарной, если  при
при  .
.
Число r называется рангом элементарной конъюнкции. В случае r = 0 конъюнкция называется пустой и полагается равной 1.
Так как каждая из n переменных  либо не входит в элементарную, либо входит в нее с отрицанием, или без отрицания, то число элементарных конъюнкций, составленных из
либо не входит в элементарную, либо входит в нее с отрицанием, или без отрицания, то число элементарных конъюнкций, составленных из  равно
равно  . Ясно, что число различных ДНФ, составленных из переменной
. Ясно, что число различных ДНФ, составленных из переменной  , равно числу подмножеств множества, из
, равно числу подмножеств множества, из  элементов, т.е.
элементов, т.е.  .
.
Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций.
Обозначим через  множество всех точек
множество всех точек  , где
, где  . Ясно, что
. Ясно, что  – множество всех вершин единичного n-мерного куба.
– множество всех вершин единичного n-мерного куба.
Сопоставим каждой булевой функции  подмножество
подмножество  из
из  , определенное следующим образом:
, определенное следующим образом:
 .
.
Например, функции, заданной следующей таблицей истинности:
| x | y | z | 
|
соответствует подмножество 
вершин трехмерного единичного куба


Данное соответствие является взаимно однозначным и обладает следующими свойствами:
1) булевой функции  соответствует подмножество
соответствует подмножество  ;
;
2) булевой функции  соответствует подмножество
соответствует подмножество  ;
;
3) булевой функции  соответствует подмножество
соответствует подмножество  .
.
Докажем свойство 2. Пусть 
Отсюда  .
.
Тогда  .
.
А это значит, что  .
.
Отсюда  .
.
Пусть  ДНФ, где
ДНФ, где  – элементарные конъюнкции. Подмножество
– элементарные конъюнкции. Подмножество  называется интервалом r-го ранга, если оно соответствует элементарной конъюнкции К r-го ранга. Как показано выше,
называется интервалом r-го ранга, если оно соответствует элементарной конъюнкции К r-го ранга. Как показано выше,  . Итак, с каждой ДНФ функции f связано покрытие
. Итак, с каждой ДНФ функции f связано покрытие  такими интервалами
такими интервалами  , что
, что  .
.
Пусть  – ранг интервала
– ранг интервала  . Тогда
. Тогда  совпадает с числом букв в ДНФ
совпадает с числом букв в ДНФ  функции
функции  .
.
Теперь ясно, что задача построения минимальной ДНФ сводится к отысканию такого покрытия подмножества  интервалами
интервалами  , чтобы число
, чтобы число  было наименьшим.
было наименьшим.
Интервал  , содержащий
, содержащий  , называется максимальным для булевой функции, если не существует интервала
, называется максимальным для булевой функции, если не существует интервала  , такого, что
, такого, что  .
.
Заметим, что соотношение  выполняется тогда и только тогда, когда элементарная конъюнкция
выполняется тогда и только тогда, когда элементарная конъюнкция  получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.
получается из элементарной конъюнкции К путем вычеркивания непустого числа сомножителей.
Очевидно, что каждый интервал  из
из  содержится в некотором максимальном интервале. Если
содержится в некотором максимальном интервале. Если  – список всех максимальных интервалов подмножества
– список всех максимальных интервалов подмножества  , то нетрудно видеть, что
, то нетрудно видеть, что  .
.
ДНФ  булевой функции f, соответствующая покрытию
булевой функции f, соответствующая покрытию
подмножества  всеми максимальными интервалами, называется сокра-
всеми максимальными интервалами, называется сокра-
щенной ДНФ функции f.
Ясно, что сокращенная ДНФ для любой булевой функции f определяется однозначно.
Пример 1 Пусть  . Обозначим
. Обозначим  ,
,  ,
,  . Найдем соответствующие этим конъюнкциям интервалы
. Найдем соответствующие этим конъюнкциям интервалы  ,
,  ,
,  .
.
Изобразим эти интервалы
 |








Очевидно, что 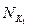 и
и 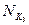 – все максимальные интервалы. Интервал
– все максимальные интервалы. Интервал  не является максимальным, ибо
не является максимальным, ибо  . Следовательно, покрытию подмножества
. Следовательно, покрытию подмножества 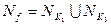 соответствует сокращенная ДНФ функции
соответствует сокращенная ДНФ функции  , равная
, равная 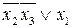 .
.
Данный геометрический подход дает и метод построения сокращенной
ДНФ.
Теперь рассмотрим аналитический метод построения сокращенной ДНФ – метод Блейка. Этот метод основан на следующей теореме.
Теорема 1Если в произвольной ДНФ булевой функции f произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получится сокращенная ДНФ функции f.
Следовательно, чтобы найти сокращенную ДНФ, надо к произвольной ДНФ данной функции применить правило обобщенного склеивания  до тех пор, пока это возможно, а затем правило поглощения.
до тех пор, пока это возможно, а затем правило поглощения.
Пример 2 Найти сокращенную ДНФ для функции  .
.
Применяя правило обобщенного склеивания, получаем: 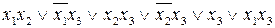 , а затем правило поглощения и находим сокращенную ДНФ:
, а затем правило поглощения и находим сокращенную ДНФ: 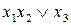 .
.
Рассмотрим еще один метод построения сокращенной ДНФ – метод Нельсона. Этот метод основан на следующей теореме.
Теорема 2Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции.
Пример 3 Найти сокращенную ДНФ для функции
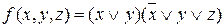 .
.
После раскрытия скобок с помощью дистрибутивного закона, получаем:
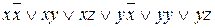 .
.
Так как 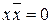 ,
, 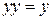 , то имеем:
, то имеем:
 .
.
Далее, применяя правило поглощения, получаем сокращенную ДНФ:
 .
.
Рассмотрим табличный метод построения сокращенной ДНФ. Этот метод основан на составлении прямоугольной таблицы (минимизирующей карты).
Минимизирующие карты для булевых функций от трех и от четырех переменных изображены в следующих таблицах:
| z x y | ||
| x4 x3 x1 x2 | ||||
| 0 0 | ||||
| 0 1 | ||||
| 1 1 | ||||
| 1 0 |
Объединяя соседние клетки, соответствующие единичным значениям булевой функции f в максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.
Пример 4 Найти сокращенную ДНФ для функции, заданной следующей таблицей.
| x4 x3 x1 x2 | ||||
| 0 0 | ||||
| 0 1 | ||||
| 1 1 | ||||
| 1 0 |
В данной таблице объединены клетки в максимальные интервалы

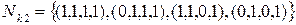
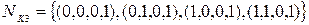

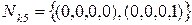 .
.
Этим интервалам соответствуют элементарные конъюнкции
 ,
,  ,
, 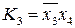 ,
,  ,
, 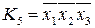 .
.
Следовательно, сокращенная ДНФ для данной функции имеет вид:
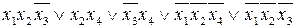 .
.
Построение сокращенной ДНФ есть только первый этап решения задачи минимизации булевой функции. В общем случае сокращенная ДНФ не является минимальной. Следующая теорема устанавливает связь между минимальной и сокращенной ДНФ.
Теорема 3Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций.
Доказательство этого утверждения следует из того факта, что покрытие подмножества  , отвечающее минимальной ДНФ, состоит только из максимальных интервалов. Действительно, если бы покрытие содержало не максимальный интервал, то его можно было бы заменить объемлющим максимальным интервалом. В результате этого сумма рангов интервалов данного покрытия уменьшилась бы, что противоречит предположению о минимальности ДНФ.
, отвечающее минимальной ДНФ, состоит только из максимальных интервалов. Действительно, если бы покрытие содержало не максимальный интервал, то его можно было бы заменить объемлющим максимальным интервалом. В результате этого сумма рангов интервалов данного покрытия уменьшилась бы, что противоречит предположению о минимальности ДНФ.
Покажем, что в классе монотонных функций понятия минимальной и сокращенной ДНФ совпадают.
Теорема 4Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции.
Пусть К – элементарная конъюнкция, входящая в сокращенную ДНФ. Предположим, что К содержит отрицание переменных. Обозначим через  произведение всех переменных, входящих в К без отрицания. Пусть
произведение всех переменных, входящих в К без отрицания. Пусть  – набор переменных, в которых всем переменным, входящим в
– набор переменных, в которых всем переменным, входящим в  , приписано значение 1, а всем остальным – значение 0. Ясно, что при этом наборе значение функции
, приписано значение 1, а всем остальным – значение 0. Ясно, что при этом наборе значение функции  равно 1. Элементарная конъюнкция
равно 1. Элементарная конъюнкция  обращается в 1 при всех наборах
обращается в 1 при всех наборах 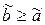 . Очевидно, что при этих наборах значение функции
. Очевидно, что при этих наборах значение функции  также равно 1. Следовательно,
также равно 1. Следовательно, 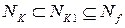 .
.
Получили противоречие с максимальностью интервала  . Итак, сокращенная ДНФ булевой функции
. Итак, сокращенная ДНФ булевой функции  не содержит отрицаний переменных.
не содержит отрицаний переменных.
Пусть  – любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами
– любая элементарная конъюнкция из сокращенной ДНФ. Конъюнкция К является единственной конъюнкцией сокращенной ДНФ, которая обращается в единицу в вершине с координатами  . Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция
. Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция 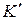 обращалась в этой вершине в 1, то не содержала бы, во-первых, букв
обращалась в этой вершине в 1, то не содержала бы, во-первых, букв  , и, во-вторых, букв
, и, во-вторых, букв 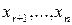 . Поэтому в конъюнкцию
. Поэтому в конъюнкцию  могли бы входить лишь буквы
могли бы входить лишь буквы 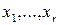 , причем не все. Но тогда
, причем не все. Но тогда  . Получили противоречие с максимальностью интервала
. Получили противоречие с максимальностью интервала  . Следовательно, для любого максимального интервала
. Следовательно, для любого максимального интервала  существует вершина куба
существует вершина куба 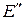 , которая покрывается только этим интервалом. Поэтому из покрытия
, которая покрывается только этим интервалом. Поэтому из покрытия  соответствующего сокращенной ДНФ, нельзя удалить ни один из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
соответствующего сокращенной ДНФ, нельзя удалить ни один из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. Действительно, в сокращенной ДНФ
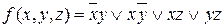
элементарная конъюнкция  поглощается дизъюнкцией остальных элементарных конъюнкций, т.е.
поглощается дизъюнкцией остальных элементарных конъюнкций, т.е. 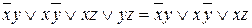 .
.
Ввиду этого введем следующее определение.
Покрытие области истинности булевой функции максимальными интервалами называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием. ДНФ булевой функции  , соответствующая неприводимому покрытию, называется тупиковой.
, соответствующая неприводимому покрытию, называется тупиковой.
Теорема 5Всякая минимальная ДНФ является тупиковой.
Доказательство этого утверждения следует из того, что покрытие, соответствующее минимальной ДНФ, является неприводимым.
Заметим, что булева функция может обладать несколькими различными минимальными ДНФ. Существуют также тупиковые ДНФ, не являющиеся минимальными ДНФ. Соответствующие примеры будут разобраны ниже.
Из того, что минимальная ДНФ является тупиковой, следует общая схема решения задачи минимизации булевых функций.
1 Выделяются все максимальные интервалы, и строится сокращенная ДНФ.
2 Строятся все тупиковые ДНФ.
3 Среди всех тупиковых ДНФ выделяются все минимальные ДНФ.
Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем:
1) для булевой функции  строим сокращенную ДНФ;
строим сокращенную ДНФ;
2) для каждой вершины 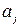 из
из 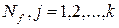 выделяем в сокращенной ДНФ функции f все такие элементарные конъюнкции
выделяем в сокращенной ДНФ функции f все такие элементарные конъюнкции  , что
, что  ;
;
3) составляем выражение вида
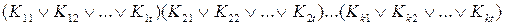 (6.1)
(6.1)
4) применяем к выражению вида (6.1) законы дистрибутивности и поглощения. В результате получаем 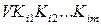 .
.
Теперь каждая ДНФ 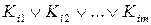 является тупиковой ДНФ функции
является тупиковой ДНФ функции  .
.
Рассмотрим работу данного алгоритма на следующем примере.
Пример 5 Рассмотрим булеву функцию, заданную следующей таблицей:
| x | y | z | 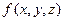
|
Найдем сокращенную ДНФ данной функции по методу Нельсона. Для этого составим КНФ данной функции 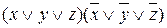 .
.
Применяя законы дистрибутивности, получаем:
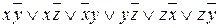 .
.
Обозначим  ,
, 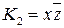 ,
, 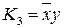 ,
, 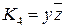 ,
, 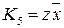 ,
,  .
.
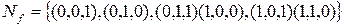
Составляем выражение (6.1)
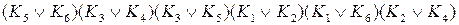 .
.
Преобразуем данное выражение к виду
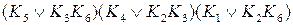 =
= 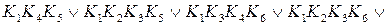
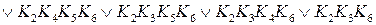 =
=  .
.
Таким образом,  имеет шесть тупиковых ДНФ:
имеет шесть тупиковых ДНФ:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) 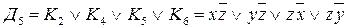 ;
;
6) 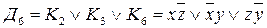 .
.
Две из них  и
и 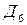 являются минимальными.
являются минимальными.