Теорема о полноте.

Цель данного параграфа дать ответ на один из основных вопросов алгебры логики – вопрос о необходимом и достаточном условиях полноты системы булевых функций. Ответ на этот вопрос дает следующая теорема, доказательство которой будет вестись по методу А. В. Кузнецова и
С. К. Яблонского.

Теорема 3 (о полноте) Для того, чтобы система булевых функций Д была полной, необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов T₀, T₁, S, M, L.

Доказательство.Необходимость. Пусть Д – полная система, целиком содержащаяся в одном из классов T₀, T₁, S, M, L. Не ограничивая общности, будем считать, что . Тогда . Следовательно, , что невозможно.

Достаточность. Пусть система булевых функций Д целиком не содержится ни в одном из классов T₀, T₁, S, M, L. Тогда в системе Д обязательно найдутся следующие функции: , не сохраняющая 0; , не сохраняющая 1; не самодвойственная функция ; нелинейная функция ; не монотонная функция . Учитывая понятие фиктивной переменной, мы можем считать, что эти функции зависят от одних и тех же переменных.

Вначале построим из системы функций Д константы 0 и 1.

Рассмотрим функцию . Эта функция есть суперпозиция функций и . Так как не принадлежит классу T₀, . Если теперь g(1) = 1, то - константа 1. Подставляя константу 1 в функцию , мы получаем константу 0, ибо .

Пусть теперь . Из равенства g(0) = 1 и g(1) = 0 заключаем, что . Возьмем несамодвойственную функцию . Очевидно, что в этом случае найдется такой набор переменных , что = .

Рассмотрим функцию и построим с помощью операции суперпозиции функцию . Тогда получаем:

(4.2)

Итак, h(0)=h(1). А это значит, что h(x) есть константа 0 или 1. Так как мы построили функцию , то суперпозиция этой функции с одной из констант дает другую константу. Следовательно, константы 0 и 1 нами построены.

Теперь, используя предыдущую теорему, мы можем с помощью суперпозиции функции и констант 0,1 построить функцию , а следовательно и все функции . Ранее мы показали, что любая булева функция может быть представлена в виде суперпозиции уже построенных функций и функций . Следовательно, для завершения доказательства теоремы нам осталось построить функцию . Для этого возьмем функцию и построим для этой функции полином Жегалкина. Так как эта функция нелинейная, то в этом полиноме найдется слагаемое, содержащее не менее двух множителей. Без ограничения общности можно считать, что этими множителями являются и . Тогда мы можем записать полином Жегалкина для функции в следующем виде:

В силу единственности полинома, функция не равна тождественно нулю. Выберем такие значения переменных , что . Ввиду этого, мы приходим к функции

где константы 0 или 1. Построим функцию следующим образом:

= .

Итак, теорема о полноте полностью доказана.

В тех задачах, где требуется выяснить, является ли данная система булевых функций полной, мы будем составлять таблицы, которые называются таблицами Поста. Данные таблицы имеют следующий вид.

	T₀	T₁	S	L	M
f₁
f₂
…	…	…	…	…	…
f_n-1
f_n

В клетках данной таблицы мы будем писать плюс или минус, в зависимости от того, входит функция, стоящая в данной строке в класс, стоящий в данном столбце, или не входит. Используя теорему о полноте, мы получаем, что для полноты данной системы булевых функций необходимо и достаточно, чтобы в каждом столбце стоял хотя бы один минус.

Пример 6 Выяснить, являются ли следующие системы булевых функций полными.

, ;

, .

Составим таблицу Поста для системы Д₁:

	T₀	T₁	S	L	M
	-	-	-	-	-

Нетрудно заметить, что .

Ясно, что не принадлежит Т₀ и Т₁. Двойственная функция к функции имеет вид: .

Следовательно, не принадлежит классу S. Найдем полином Жегалкина для функции : .

Следовательно, функция не принадлежит классу L. Так как , а , то не принадлежит классу М.

Итак, система является полной.

Составим таблицу Поста для системы Д₂:

T₀	T₁	S	L	M
+	+	+	+	–
+	+	–	–	+
+	–	–	+	+
–	+	–	+	+

Исследуем функцию . Легко проверить, что она принадлежит классам Т₁, Т₀, L. Покажем, что она является самодвойственной.

Функция не монотонна, так как , а . В каждом столбце таблица Поста для системы Д₂ стоит минус. Следовательно, система Д₂ является полной.

Составим таблицу Поста для системы Д₃:

T₀	T₁	S	L	M
–	+	–	–	–
–	–	+	+	–

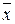
Из таблицы видно, что система Д₃ является полной.

Составим таблицу Поста для системы Д₄:

	T₀	T₁	S	L	M
	-	-	+	-	-

Исследуем функцию .

Легко проверить, что данная функция не принадлежит ни Т₀, ни Т₁. Так как , а значение функции при наборе (0,0,0) больше, чем при наборе (1,1,1), то функция не монотонна. Очевидно, что все переменные данной функции являются существенными. А так как данная функция не может совпадать ни с , ни с , то она нелинейная. Как и в примере 6, можно показать, что функция является самодвойственной. Следовательно, система Д₄ не является полной.

Назовем систему булевых функций несократимой, если из нее нельзя исключить ни одной функции так, чтобы оставшаяся после исключения система снова была полной.

Очевидно, что любую полную систему булевых функций можно свести к несократимой. Как следует из теоремы о полноте, в любой несократимой полной системе содержится не более 5 функций. Следующая теорема показывает, что в действительности их число всегда может быть сокращено до 4.

Теорема 4Максимальное возможное число функций в несократимой полной системе булевых функций равно 4.

Действительно, при доказательстве теоремы о полноте мы видели, что из любой полной системы булевых функций можно выделить полную подсистему, содержащую не более пяти функций. Причем, функция , не сохраняющая 0, либо не сохраняет 1, либо если является самодвойственной. Следовательно, кроме этой функции достаточно оставить в системе лишь три функции: нелинейную, немонотонную либо функцию, не сохраняющую 1, либо несамодвойственную функцию.