Важнейшие замкнутые классы.

Система булевых функций называется полной, если любую булеву функцию можно представить в виде суперпозиции функций из Д.

Приведем пример полных систем.

Пример 1 Как отмечено выше, система является
полной.

Пример 2 Множество всех булевых функций P₂ является полной системой.

В вопросе о полноте важную роль играет следующая теорема.

Пусть и системы булевых функций. Если Д₁ – полная система и каждая ее функция выражается в виде суперпозиции функций из Д₂, то система Д₂ также является полной.

Действительно, так как Д₁ – полная система, то любая булева функция представима в виде суперпозиции функций из Д₁. А так как любая функция из Д₁ представима в виде суперпозиций функций из Д₂, то Д₂ – полная система.

Пример 3 Система – полная.

Это следует из предыдущей теоремы и из примера 1, ибо . Аналогичным образом получаем полноту системы . Приведенные примеры говорят о том, что существуют различные полные системы булевых функций. Каждая из таких систем может быть принята в качестве набора «элементарных» функций, и любая булева функция может быть выражена в виде суперпозиции через «элементарные» функции принятого набора.

С понятием полноты тесно связано понятие замкнутого класса и замыкания.

Множество Т булевых функций называется замкнутым классом, если любая суперпозиция функций из Т снова принадлежит Т.

Всякая система М булевых функций порождает некоторый замкнутый класс. Этот класс состоит из всех булевых функций, которые можно получить суперпозициями из М. Такой класс называется замыканием М и обозначается [М]. Для замкнутого класса М следует, что [М] = М. Очевидно, что если М – полная система, что [М] = Р₂.

При установлении необходимого и достаточного условия полноты важную роль играют пять замечательных классов булевых функций, которые будут рассмотрены ниже.

Первый замечательный класс – класс булевых функций, сохраняющих константу С, т.е. функций , для которых .

Подсчитаем число таких булевых функций от n переменных. Поскольку на нулевом наборе значение функций из Т₀ фиксировано, то в Т₀ содержится ровно булевых функций от n переменных.

Ясно, что функции принадлежат классу Т₀, а 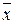не принадлежит Т₀. Следовательно, .

Второй замечательный класс – класс булевых функций, сохраняющих константу 1, т.е. функций , для которых .

Как и выше, легко подсчитать число таких функций от переменных. Их

ровно .

Ясно, что функции принадлежат классу Т₁, а функция – нет. Следовательно, .

Третий замечательных класс – класс всех самодвойственных функций S.

Булева функция называется самодвойственной, если она совпадает со своей двойственной, т.е. .

Пример 4 Доказать, что функция является самодвойственной.

Двойственная для данной функции есть функция . Теперь, применяя закон де Моргана, получаем:

Используя законы дистрибутивности и идемпотентности, имеем:

Следовательно, искомая функция самодвойственна.

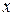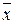Очевидно, что и принадлежат классу S, а , не принадлежат классу S. Следовательно, .

Подсчитаем число всех самодвойственных функций от n переменных.

Так как самодвойственная функция на наборах и принимает противоположные значения, то она полностью определяется своими значениями, принимаемыми ею на половине всех наборов переменных. Следовательно, число самодвойственных функций от переменных равно .

Четвертый замечательный класс – класс всех линейных булевых функций.

Булевы функции вида , где и равны нулю или единице, называют линейными.

Нетрудно подсчитать число всех линейных булевых функций от переменных. Их число равно .

Очевидно, что функции принадлежат L, а функция xy не принадлежит L. Следовательно .

Для того, чтобы определить, является данная булева функция линейной или нет, ее надо представить в виде полинома Жегалкина.

Пример 5 Выяснить, является ли функция линейной. Запишем данную функцию в виде полинома Жегалкина:

.

Следовательно, функция не является линейной.

Пятый замечательный класс – класс М всех монотонных булевых функций.

Два набора и называются сравнимыми, если .

Запись означает, что набор предшествует набору . Например, , а наборы и несравнимы.

Булева функция называется монотонной, если для любых наборов и таких, что , имеет место неравенство .

Очевидно, что константы 0,1 и функция х – монотонные функции.

Функции – монотонные функции (доказательство осуществляяется проверкой).

Функции не являются монотонными, так как , а .

Следовательно, .

Для распознавания монотонности функции полезной является следующая теорема.

Теорема 1Булева функция, имеющая дизъюнктивную нормальную форму, не содержащую отрицаний, является монотонной функцией, отличной от 0 и 1.

Докажем данную теорему. Пусть булева функция имеет дизъюнктивную нормальную форму Д, не содержащую отрицаний, и пусть на наборе , . Тогда Д содержит конъюнкцию равную единице на наборе . Следовательно, . Возьмем любой набор такой, что . В нем обязательно . Поэтому конъюнкция при этом наборе равна 1, а значит . Итак, условие монотонности для ДНФ Д выполнено. А это значит, что функция монотонна.

Используя данную теорему, сразу получаем, что функции являются монотонными.

Классы булевых функций являются замкнутыми классами.

Докажем, что – замкнутый класс. Для этого надо показать, что функция принадлежит , если функция f, принадлежит . Это следует из следующей цепочки неравенств:

.

Аналогичным образом доказывается замкнутость класса .

Если самодвойственные функции, то . Итак, S – замкнутый класс.

Пусть , где – монотонные функции, и

пусть их наборы переменных. Здесь переменные функции Ф состоят из функций . Пусть и два таких набора, что . Каждый из наборов и однозначно определяет следующие наборы значений переменных . Причем . Так как – монотонные функции, то . Следовательно, . Из монотонности функции f получаем, что .

Итак, М – замкнутый класс.

Замкнутость класса L следует непосредственно из определения линейных функций.

Как показано выше, функция 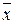не принадлежит классу М. Следующая теорема показывает, что всякая немонотонная функция содержит, в некотором смысле, в своем составе функцию отрицания.

Теорема 2Если – немонотонная функция, то в результате ее суперпозиции с константами 0 и 1 может быть получена функция отрицания одного из аргументов функции .

Докажем данную теорему. Так как функция немонотонная, то найдутся два набора и значений переменных таких, что , и . Причем, в качестве этих наборов и можно выбрать соседние наборы, т.е. наборы, отличающиеся значениями только по одной из координат. Действительно, если и не являются соседними наборами, то набор отличается от набора в t координатах, где t > 1. Причем, эти координаты в наборе равны 0, а в наборе равны 1. Из этого следует, что между наборами и можно вставить t – 1 наборов , таких, что

. (4.1)

Так как , то обязательно найдется такая пара соседних наборов из цепочки (4.1) и , что . Не ограничивая общности, мы можем считать, что ;

.

Подставим в функцию вместо переменной константу , где . В результате мы получим функцию от одной переменной:

А это значит, что . Следовательно, .