Алгебра Жегалкина.

Множество булевых функций, рассматриваемое вместе с операциями конъюнкции и сложения (по модулю два), будем называть алгеброй Жегалкина.

Непосредственно проверкой (с помощью таблиц истинности) устанавливаются следующие законы:

1) – закон коммутативности;

2) – закон ассоциативности;

3) – закон дистрибутивности;

4) ;

5) .

В алгебре Жегалкина роль совершенных нормальных форм булевой алгебры играют полиномы Жегалкина.

Полиномом Жегалкина называется полином вида

причем в каждом наборе все координаты различны, а суммирование ведется по некоторому множеству таких не совпадающих наборов,
а – константа 0 или 1.

Например, выражение является полиномом Жегалкина, а выражения и – нет, так как в первом выражении имеется конъюнкция, содержащая две переменные y, а второе выражение содержит два одинаковых слагаемых и .

Если в произвольной форме алгебры Жегалкина раскрыть скобки и произвести все возможные упрощения по указанным выше законам и закону идемпотентности, то получится формула, являющаяся полиномом Жегалкина.

Рассмотрим теперь взаимосвязь, существующую между операциями булевой алгебры и алгебры Жегалкина. Непосредственной проверкой устанавливается

 

(3.7)

Ранее мы показали, что любая булева функция может быть выражена в виде формулы через отрицание, конъюнкцию и дизъюнкцию. Согласно законам (3.7) получаем, что любая булева функция может быть выражена в виде формулы алгебры Жегалкина. Следовательно, существование полинома Жегалкина доказано для любой булевой функции.

Число различных слагаемых (конъюнкций) полинома Жегалкина от n переменных равно числу всех подмножеств из n элементов, т.е. 2ⁿ. Число различных полиномов, которые можно образовать из этих конъюнкций, равно числу всех подмножеств множества данных конъюнкций, т.е. 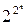. Следовательно, число всех полиномов Жегалкина от n переменных равно числу всех булевых функций от n переменных. Отсюда следует единственное представление булевой функции посредством полинома Жегалкина. Итак, справедлива следующая теорема.

Теорема 6Каждая булева функция может быть единственным образом выражена при помощи полинома Жегалкина.

Пример 8 Выразить в виде полинома Жегалкина.

Способ 1 (табличный) Ищем требуемый полином методом неопределенных коэффициентов: .

1) при x = y = 0 имеем: d = 1;

2) при x = 0, y = 1 имеем: a = 0;

3) при x = 1, y = 0 имеем: b = 1;

4) при x = 1, y = 0 имеем: 1 = a + b + c + d = a + 1 + 0 + 1 = a, т.е. а = 1.

Отсюда

Способ 2

 

Вопросы для самоконтроля

1 Сформулируйте теорему о разложении и следствие из нее.

2 Дайте определение СДНФ.

3 Приведите алгоритмы построения СДНФ.

4 Дайте определение СКНФ.

5 Приведите алгоритмы построения СКНФ.

6 Дайте определение ДНФ.

7 Как найти ДНФ?

8 Дайте определение КНФ.

9 Как найти КНФ?

10 Какая формула алгебры логики называется тождественно истинной?

11 Какая формула алгебры логики называется тождественно ложной?

12 Какая формула алгебры логики называется выполнимой?

13 Что называется проблемой разрешимости?

14 Сформулируйте методы решения проблемы разрешения.

15 Что называется алгеброй Жегалкина?

16 Сформулируйте законы алгебры Жегалкина.

17 Что называется полиномом Жегалкина?

18 Сформулируйте алгоритмы построения полиномов Жегалкина.