Равносильные формулы алгебры логики.
Приведем определение формулы алгебры логики.
1) каждая «элементарная» булева функция – формула;
2) если некоторое выражение N есть формула, то 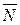 тоже формула;
тоже формула;
3) если некоторые выражения M и N есть формулы, то выражения  ,
, 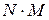 ,
,  ,
,  тоже формулы;
тоже формулы;
4) других формул, кроме построенных по п.п.1), 2), 3), нет.
Формулы алгебры логики мы будет обозначать большими N, M, … Например, следующие выражения являются формулами алгебры логики:
 ,
,  .
.
С целью упрощения формул, условимся, что операция конъюнкции «сильнее» операций дизъюнкции, импликации и эквивалентности, т.е. если нет скобок, то вначале выполняется операция конъюнкции.
Формула алгебры логики определяет некоторую булеву функцию, значение которой совпадает со значениями данной формулы для всех наборов значений переменных.
Две формулы N и M называются равносильными, если они определяют одну и ту же булеву функцию (запись N = M будет означать, что формулы N и M равносильны).
Пример 1 Формулы 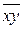 и
и 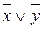 равносильны, т.е.
равносильны, т.е. 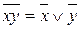 .
.
Действительно, построим таблицы истинности для данных формул.
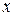
| 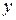
| 
| 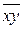
| 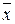
| 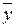
| 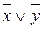
|
Из таблиц видно, что формулы 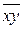 и
и  определяют одну и ту же булеву функцию и, следовательно, являются равносильными.
определяют одну и ту же булеву функцию и, следовательно, являются равносильными.
Очевидно, что отношение равносильности формул алгебры логики является:
1) рефлексивным, т.е. N = N для любой формулы N;
2) симметричным, т.е. если N = M, то M = N для любых формул N и M;
3) транзитивным, т.е. если N = M и M = J, то N = J для любых формул N,M,J.
Таким образом, отношение равносильности является отношением эквивалентности.
Если какую-нибудь формулу N1, являющуюся частью формулы N заменить формулой N2, равносильной N1, то полученная формула окажется равносильной N. Это свойство лежит в основе преобразования формул с целью их упрощения или приведения к определенной форме.
При преобразовании формул алгебры логики используются свойства логических операций, которые будут рассмотрены ниже.
2.2 Законы алгебры логики.
Приведем перечень важнейших равносильностей (законов) алгебры логики. Эти равносильности выражают свойства логических операций.
1)  – закон тождества;
– закон тождества;
2)  – закон противоречия;
– закон противоречия;
3) 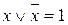 – закон исключительного третьего;
– закон исключительного третьего;
4)  – закон двойного отрицания;
– закон двойного отрицания;
5)  ,
, 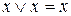 – законы идемпотентности;
– законы идемпотентности;
6) 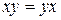 ,
,  – законы коммутативности;
– законы коммутативности;
7) 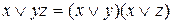 ,
,  – законы дистрибутивности;
– законы дистрибутивности;
8)  ,
,  – законы ассоциативности;
– законы ассоциативности;
9) 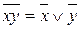 ,
, 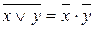 – законы де Моргана;
– законы де Моргана;
10) 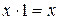 ,
, 
11)  ,
, 
12)  ,
,  – законы поглощения;
– законы поглощения;
13)  ,
,  – законы склеивания.
– законы склеивания.
Перечисленные законы алгебры логики доказываются с помощью таблиц истинности. В качестве примера докажем справедливость закона 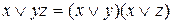 .
.
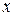
|  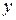
| 
| 
| 
| 
| 
| 
|
Из таблиц видно, что формулы  и
и  определяют одну и ту же булеву функцию. Следовательно, они равносильны.
определяют одну и ту же булеву функцию. Следовательно, они равносильны.
Логические операции – конъюнкция, дизъюнкция, импликация и эквивалентность, вообще говоря, не являются независимыми друг от друга.
В самом деле,
 ,
,  ;
;
 ,
,  .
.
Первые две равносильности легко доказываются с помощью таблиц истинности. Две последние равносильности докажем с помощью законов де
Моргана и двойного отрицания:
 ;
;  .
.
Итак, справедливы следующие утверждения:
1) импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание;
2) конъюнкцию можно выразить через дизъюнкцию и отрицание;
3) дизъюнкцию можно выразить через конъюнкцию и отрицание;
4) все операции посредством равносильных выражений можно заменить двумя: конъюнкцией и отрицанием или дизъюнкцией и отрицанием.
Естественно возникает следующий вопрос. Для чего вводить пять логических операций, когда можно обойтись двумя? Использование лишь двух операций существенным образом усложнило бы запись, что привело бы к громоздким формулам. Однако в некоторых приложениях математической логики удобно ограничиться двумя операциями. Аналогичная ситуация имеет место в арифметике. Всякое натуральное число можно записать с помощью цифр 0 и 1. Однако записи чисел и выкладки в двоичной системе громоздки. К этой системе прибегают лишь в некоторых случаях.
Множество булевых функций, рассматриваемое вместе с операциями отрицания, конъюнкции и дизъюнкции, называют булевой алгеброй. Законы 1-13 являются основными законами булевой алгебры.
Обратим внимание на характер соответствий между равносильностями, объединенными в пару под номерами (5-13). В этих соответствиях проявляется так называемый закон двойственности.
Назовем формулу алгебры логики  двойственной к формуле
двойственной к формуле  , если
, если  =
=  .
.
Будем говорить, что операция конъюнкции двойственна операции дизъюнкции и наоборот.
Как показано в пункте 2.2, всякая формула алгебры логики может быть
приведена равносильными преобразованиями к формуле, содержащей только операции конъюнкции, дизъюнкции и отрицания. Поэтому, учитывая законы де Моргана и двойного отрицания, две формулы алгебры логики N и M, содержащие только операции конъюнкции, дизъюнкции и отрицания, будут двойственными, если одна получается из другой заменой каждой операции на двойственную и 1 заменяется на 0, а 0 на 1.
Например, формула  двойственная к формуле
двойственная к формуле  , а формула
, а формула  двойственная к формуле
двойственная к формуле  .
.
Теперь сформулируем закон двойственности.
Теорема 1Если формулы алгебры логики N и M равносильны, то и двойственные им формулы N* и M* равносильны.
Докажем данный закон. Пусть N(x1,x2,…,xn) = M(x1,x2,…,xn). Согласно определению двойственной формулы
 и
и  .
.
Так как N(x1,x2,…,xn) и M(x1,x2,…,xn) принимают одинаковые значения при любых значениях переменных x1,x2,…,xn, то
 =
=  .
.
Отсюда следует, что
 .
.
Так как формулы  и
и  равносильны соответственно формулам
равносильны соответственно формулам  и
и  , то они равносильны между собой.
, то они равносильны между собой.
Принцип двойственности позволяет сократить усилие на вывод равносильностей.
Пример 2 Из равносильности 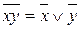 вытекает равносильность
вытекает равносильность
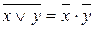 . Из равносильности
. Из равносильности 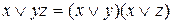 вытекает равносильность
вытекает равносильность  .
.
Вопросы для самоконтроля
1 Дайте определение формулы алгебры логики.
2 Какие формулы алгебры логики называются равносильными?
3 Сформулируйте законы алгебры логики.
4 Какая формула алгебры логики называется двойственной к данной формуле алгебры логики?
5 Сформулируйте принцип двойственности.