Булевы функции.
Пусть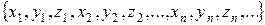 
исходный алфавит переменных.
Функцией алгебры логики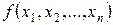 
от переменных 
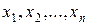называется функция, принимающая значения 1, 0 и аргументы которой также принимают значения 1, 0.
Обычно функции алгебры логики называют булевыми функциями. Название «булевы функции» возникло в связи с использованием функций рассматриваемого типа в алгебре логики, начало которой было положено трудами ирландского ученого 19 века Дж. Буля. Областью определения булевой функции от n переменных служит совокупность всевозможных
n-мерных упорядоченных наборов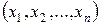 
, где 
.
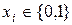Следует отметить, что любой такой набор можно рассматривать как представление некоторого целого неотрицательного числа в двоичной системе счисления. Например, набору (0,1,0,1) соответствует число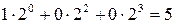 
, а набору (1,1,1) – число 
.
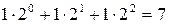Все наборы размерности n нумеруются целыми числами от 0,2n-1. Отсюда нетрудно заметить, что число таких наборов равно 2n.
Всякая булева функция от n переменных может быть задана с помощью таблицы истинности:
| x1 | x2 | … | xn-1 | xn | f(x1,x2,…,xn-1,xn) |
| … | f (0,0,…,0,0) | ||||
| … | f (0,0,…,0,1) | ||||
| … | f (0,0,…,1,0) | ||||
| … | … | … | … | … | … |
| … | f (1,1,…,1,1) |
Данная таблица состоит из 2n строк, причем в ней все наборы 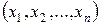расположены в порядке возрастания их номеров.
Очевидно, что булевы функции от n переменных однозначно определяются своими последними столбцами из этой таблицы, т.е. наборами из 2n нулей и единиц. Следовательно, различных булевых функций от n переменных будет столько, сколько имеется различных наборов длины 2n, а их число равно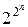 
. Итак, мы доказали следующую теорему:
Теорема 1Имеется точно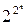 
булевых функций от 
переменных.
В алгебре логики особое значение имеют следующие булевы функции, которые называют элементарными булевыми функциями:
1) 
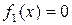– константа 0;
2) 
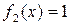– константа 1;
3) 
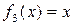– тождественная функция;
4) 
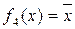– отрицание х;
5) 
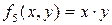– конъюнкция x и y;
6) 
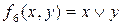– дизъюнкция х и у;
7) 
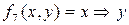– импликация х и у;
8) 
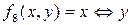– эквивалентность х и у;
9) 
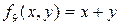– сложение х и у по mod2;
10) 
– функция Шеффера;
11) 
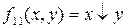– стрелка Пирса.
Последние три функции задаются следующими таблицами истинности:
| 
| 
| 
| 
|
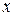
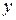
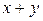
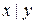
Введенное понятие булевой функции несовершенно тем, что оно не позволяет рассматривать функцию от меньшего числа аргументов как функцию от большего числа аргументов. Для устранения этого недостатка введем понятие фиктивной переменной.
Переменная xi в функции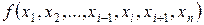 
называется фиктивной, если 
= 
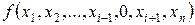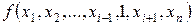при любых значениях остальных переменных. В этом случае функция 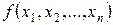, по существу, зависит от (n-1) – переменной, т.е. представляет собой функцию 
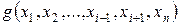от (n-1) переменной. Говорят, что функция g получается из функции f удалением фиктивной переменной, а функция f получается из g введением фиктивной переменной, причем эти функции являются равными.
Благодаря введению фиктивных переменных любую булеву функцию от переменных можно считать функцией от любого большего числа переменных. Поэтому любую конечную совокупность булевых функций можно считать зависящими от одного и того же числа переменных.
Вопросы для самоконтроля
1 Дайте определение основных логических операций булевой алгебры.
2 Дайте определение булевой функции.
3 Что такое таблицы истинности булевой функции?
4 Каково число булевых функций от 
переменных?
5 Какие булевы функции называются элементарными?