Часть I.

За каждое правильно выполненное задание начисляется два балла, в противном случае – ноль баллов.

 

I.Пусть существуют конечные пределы 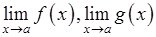, тогда справедливы утверждения:

1.если и , то возможно, что Нет

2.если и , то найдется такая окрестность точки 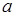, для каждого из которой Да

3.если то найдется такая окрестность точки 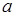, для которой ограничена Да

4.если и , то Да

 

II.Функция 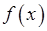является бесконечно малой в точке , если:

5. Нет

6. Да

7. Да

8. Нет

 

III.Функция 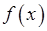является бесконечно большой в точке , если:

9. Да

10. Нет

11. Нет

12. Да

 

 

IV.Функция 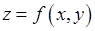имеет точку локального экстремума, если:

13. Да

14. Нет

15. Нет

16. Да

 

V.Функция 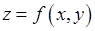ограничена на плоскости, если:

17. Да

18. Да

19. Да

20. Нет

 

 

VI.Если и , то неопределенный интеграл обладает свойством:

21. Нет

22. Да

23. Да

24. Нет

 

VII.Если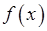и непрерывные функции, для всех , то справедливы утверждения:

25. Нет

26. Да

27. для всех Нет

28.Найдутся такие и такие, что

Да