Ответ: Нет
Задание II. Функция 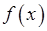 является бесконечно малой в точке
является бесконечно малой в точке  , если:
, если:
5. 
6. 
7. 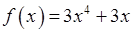
8. 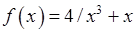
Решение. Функция 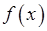 называется бесконечно малой при
называется бесконечно малой при 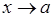 , где
, где 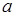 может быть числом или одной из величин
может быть числом или одной из величин  , если
, если  .
.
Бесконечно малой функция может быть только в том случае, если указать к какой величине стремится аргумент  . При различных значениях
. При различных значениях 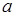 функция может быть бесконечно малой или нет.
функция может быть бесконечно малой или нет.
Свойства бесконечно малых:
a)Сумма конечного числа бесконечно малых функций при 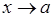 тоже бесконечно малая функция при
тоже бесконечно малая функция при 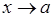 .
.
b)Произведение конечного числа бесконечно малых функций при 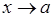 тоже бесконечно малая функция при
тоже бесконечно малая функция при 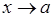 .
.
c)Произведение бесконечно малой функции на функцию, ограниченную вблизи точки  является бесконечно малой функцией при
является бесконечно малой функцией при 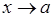 .
.
d)Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть бесконечно малая функция.
5.Находим пределы 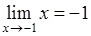 и
и 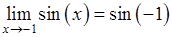 , следовательно
, следовательно
 .
.
Вывод. Функция  не является бесконечно малой в точке
не является бесконечно малой в точке  .
.